无协调主体的多产消者完全端到端交易机制
2023-02-27吴毓峰杨胜春潘振宁刘前进邱星宇
吴毓峰,杨胜春,潘振宁,余 涛,刘前进,邱星宇
(1. 华南理工大学电力学院,广东省广州市 510641;2. 广东省电网智能量测与先进计量企业重点实验室,广东省广州市 510641;3. 中国电力科学研究院有限公司(南京),江苏省南京市 210003)
0 引言
新能源高比例渗透与储能技术普及是未来电力系统发展的必然趋势[1-3]。传统负荷将向具有源荷二重性的产消者转变[4-5],由此带来的双向潮流等问题使电力系统的网络复杂性不断提高。因此,能量交易(transactive energy,TE)[6]作为实现产消者供需就地平衡的有效机制受到广泛关注。
交易机制根据是否存在协调控制中心可分为集中调度机制[7-8]、弱中心化交易机制[9-10]、完全端到端交易机制等。按定价机制又分为统一定价[11-12]、自主定价等方式。其中,集中式机制较为成熟,但其要求优化主体掌握系统全部信息,这并不现实。同时,产消者的增加使集中求解可能出现维数爆炸现象。相比之下,端到端交易机制可降低计算难度,充分考虑产消者诉求,是更为理想的能量交易方式[11]。
以供需比(supply demand ratio,SDR)方法制定交易价格是实现端到端交易的常见方式[12-13]。文献[12]以光伏产消者为对象,根据SDR 制定电价,实现端到端交易。文献[13]将补偿价格引入SDR,以提高产消者参与交易的积极性。这类研究需提前确定产消者买/卖方身份,未考虑其灵活性[14]。此外,统一的价格忽略了各主体支付意愿的差异。
产消者竞争决策属于非合作不完全信息博弈[15-17]。在文献[15]中,买卖双方各自博弈得出需求,并上传至市场运营商进行调度。文献[16]将多微网系统作为领导者、微网聚合商作为跟随者,采用主从博弈实现综合能源微网优化调度。文献[17]将主从博弈应用于买卖双方的交易中。但这类研究在信息更新机制不合理时,博弈可能无法达到均衡[17]。
上述产消者信息的交互更新普遍依赖于第三方主体,这将增加信息泄露风险,需要成熟的监管制度以保证第三方主体公信力。同时,未来产消者交易可呈现为大规模和大批量小规模交互,这对第三方主体在安全稳定、计算以及多线程处理能力方面有着严格要求。文献[18]利用拉格朗日对偶变换与次梯度下降法对多微网系统解耦,但仅讨论了孤岛系统下的交易问题。文献[14]用类似思想讨论了并网运行下智能园区产消者交易问题。由于多数研究未考虑物理约束,文献[19]提出带物理约束的交易机制,但其潮流校核依赖于全局信息。文献[20]在交易中考虑电压约束,但需构建信息分支树以协调产消者优化。 文献[21-22]由配电网管理者(distribution system operator,DSO)与下层产消者构成双层优化模型,但其同样依赖于DSO 对全局信息的把握。同时,配电网分析中产消者常被简化为节点,但其内部物理约束客观存在。若忽略这些约束,则难免有产消者策略无效的情况。
综上,本文提出一种考虑物理网络约束的完全端到端交易机制。以微网为对象,考虑物理约束建立优化模型;引入支路撕裂法和拉格朗日对偶分解法实现主体解耦,并基于交替方向乘子法(alternating direction method of multipliers,ADMM)建立交易框架。在此框架下,各主体自主参与端到端交易,仅向关联主体传递边界信息,在内部进行优化即可实现全局最优。相比其他研究,本文各主体市场身份随外部状态与内部条件动态变化,交易价格符合实际市场规律。同时,可不依赖第三方主体即可确保交易策略的可行性。通过减少信息交互次数,降低隐私泄露的风险。
1 无协调主体下多产消者端到端交易框架
2 产消者模型构建
微网具有典型源荷二重性,故本文以其为对象展开分析讨论。微网内部资源有分布式发电机(distributed generator,DG)、光 伏(photovoltaic,PV)、风 力 机(wind turbine,WT)、储 能(energy storage system,ESS)与 柔 性 负 荷(flexible load,FL)。全文调度间隔Δt设置为1 h。
2.1 DG 模型
DG 成本函数与约束条件表示如下:

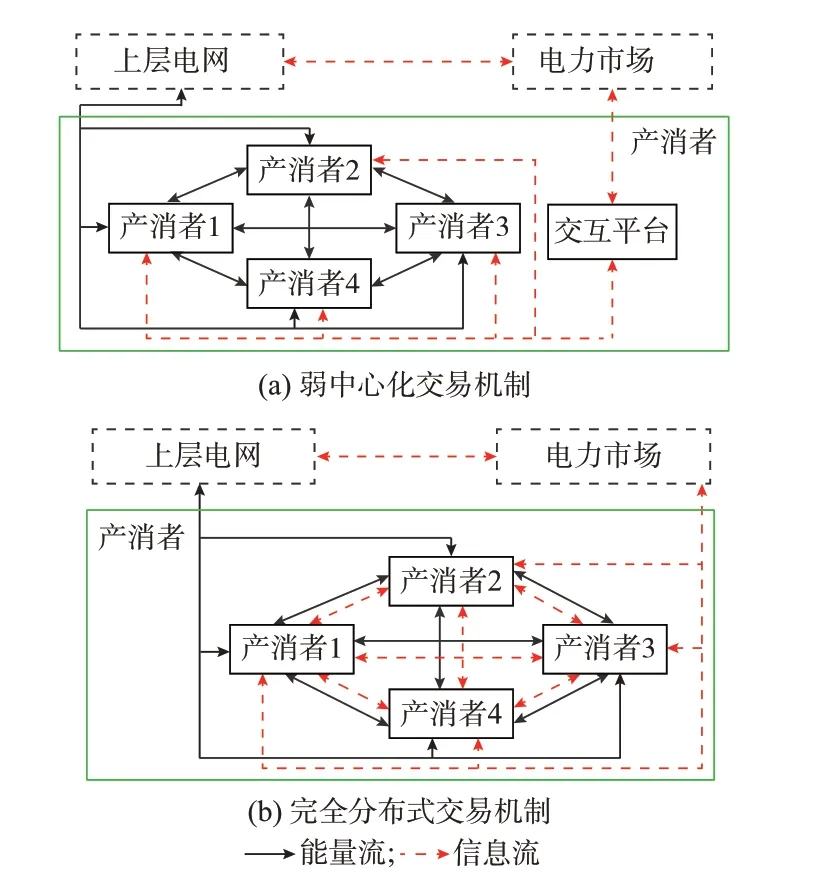
图1 不同交易机制的框架Fig.1 Framework of different transaction mechanisms

2.2 PV 和WT 模 型
本文考虑PV、WT 采用最大功率跟踪方式,全额接纳风光出力,且认为其不会造成额外成本。

2.3 ESS 模型
ESS 的运行约束及成本可表达如下:
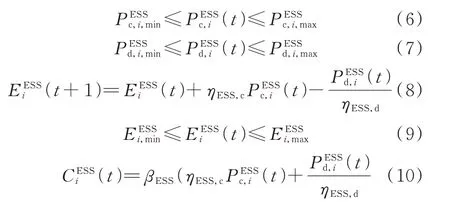


2.4 FL 模型
为保证产消者生活需求和生产任务,暂考虑可转移负荷,即周期内总用电量不变的可灵活转移负荷[24]。以二次函数建立满意度成本模型[25]:

2.5 物理网络潮流约束模型
引入简化线性DistFlow 潮流方程[26]:
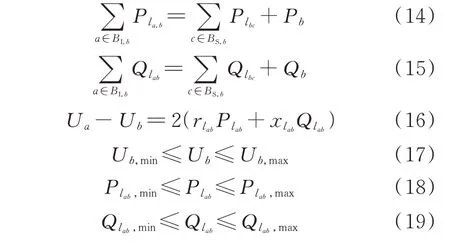
式中:BI,b和BS,b分别为沿参考方向注入、流出节点b的节点集合;Plab和Qlab分别为节点a与节点b间支路lab的有功功率和无功功率,支路功率需要满足潮流上下限约束式(18)与式(19);Plbc和Qlbc分别为节点b与节点c间支路lbc的有功功率和无功功率;Pb和Qb分别为节点b的有功功率和无功功率;rlab和xlab分别为支路lab的电阻和电抗;Ub为节点b的电压,需满足节点电压上下限约束式(17);Plab,max和Qlab,max分别为支路lab的有功功率上限和无功功率上限;Plab,min和Qlab,min分别为支路lab的有功功率下限和无功功率下限;Ub,max和Ub,min分别为节点b的电压上限和下限。
3 端到端交易模型
购售电行为可同时发生在产消者间及产消者与上层电网间。其中,各主体间联络线应由电网公司批准投资,产权归其所有。因此,各主体需要根据交易功率支付过网税费(买方卖方平均承担)。
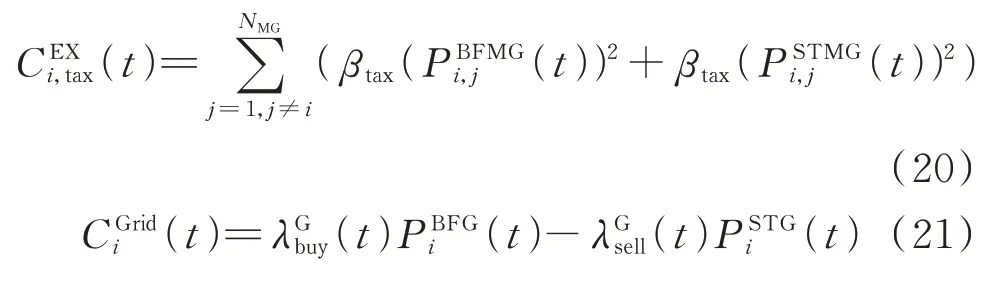
本文中联络线是端到端交易的基础,当联络线不存在时式(28)等于0。
综上,以最小化全体微网的运行成本为优化目标进行日前优化,可构建目标函数如下:

分析上述集中式问题可知,潮流约束的校核需掌握系统全局信息,主体的耦合体现于潮流与式(28)2 个约束。故不同于文献[19]仅对交易功率约束(28)进行处理,本文引入支路撕裂法在联络线上增设虚拟节点,实现各主体解耦[27],如图2 所示。图中,Grid、DG、WT、L、BS、PV 分别表示电网、分布式发电机、风力机、负荷、电池储能、光伏。其中,
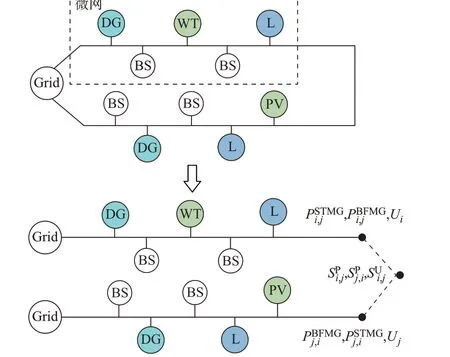
图2 两微网下的支路撕裂法示意图Fig.2 Schematic diagram of branch tearing method in two microgrids

利用ADMM 进行求解。引入拉格朗日乘子对式(31)至式(34)进行解耦,并用P、S、λ分别表示所有功率、全局变量和乘子组成的向量,可得到增广拉格朗日函数:

用γ表示P的可行域,可得第k次迭代更新式(36)至式(38)。具体的推导过程、各式的完整形式及各主体需求解的子问题见附录A。
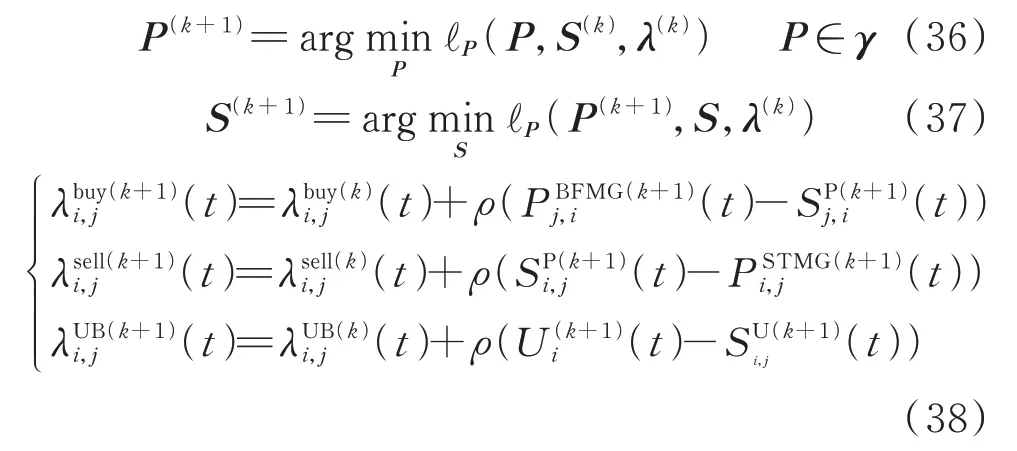
该问题属于经典2-block 凸规划问题,ADMM

式中:ε为收敛精度。
式(35)表明各主体优化变量Pi(t)无耦合,故式(36)可分解为各微网的独立子问题,如附录A 所证。式(38)表明乘子更新可在相邻主体间完成,但式(37)的求解需要掌握所有主体信息P。因此,本文将式(37)等价转化为式(40)和式(41)(推导见附录C)。相邻主体交易边界变量即可更新变量S。

各主体仅需以最小化运行成本和购售电成本为目标进行求解即可。在物理网络约束方面,通过对联络线有功功率及电压的解耦,各主体仅需在内部考虑潮流约束即可保证交易的可行性。

综上,本文所提无协调主体的多产消者完全端到端交易机制的交易框架如附录D 表D1 的伪代码所示。
4 算例分析
4.1 算例设置
以含4 个微网的17 节点区域配电网进行分析,其结构如图3 所示。

图3 17 节点配电网拓扑Fig.3 Topology of 17-node distribution network
图 中,MG1 至MG4、ESS1 至ESS4、RES1 至RES4、DG1 至DG4、Load1 至Load4 分别表示微网1至微网4、微网1 至微网4 中的储能、可再生能源、分布式发电机、负荷。各微网负荷需求和新能源最大出力见附录D 图D1,具体参数见附录D 表D2 与表D3。算例基于Python 3.6 语言编写,在配置为Core i7 CPU 和16 GB 内存的计算机上以Spyder 编译平台完成仿真。算例中优化问题的求解全部基于Cplex 求解器。
算例中微网1 含有WT,而其余微网皆为PV 接入。将1 d 分为24 个调度间隔进行日前调度优化,微网内部资源出力及电能交易情况分析如附录E 图E1 至图E5 所示。该结果表明,本文所提机制能有效引导微网进行资源配置。
4.2 迭代收敛情况及交易价格分析
各微网成本的迭代结果见附录E 图E6。如附录B 所证,经50 次迭代,本文机制已呈现出收敛趋势。本文最终目标为实现各微网自主交易,在保护隐私的同时形成有效的端到端能量交易,故本文机制是否有效在于最终交易价格的合理与否。
如图4 所示,各微网的交易价格都在主网购售电价格之间,与客观的经济规律一致。交易电价高于向主网购电价格时,功率缺额的用户将向成本更低的上层电网购电。交易电价低于向主网售电价格时,功率盈余的用户则向上层电网售电以获取更大收益。
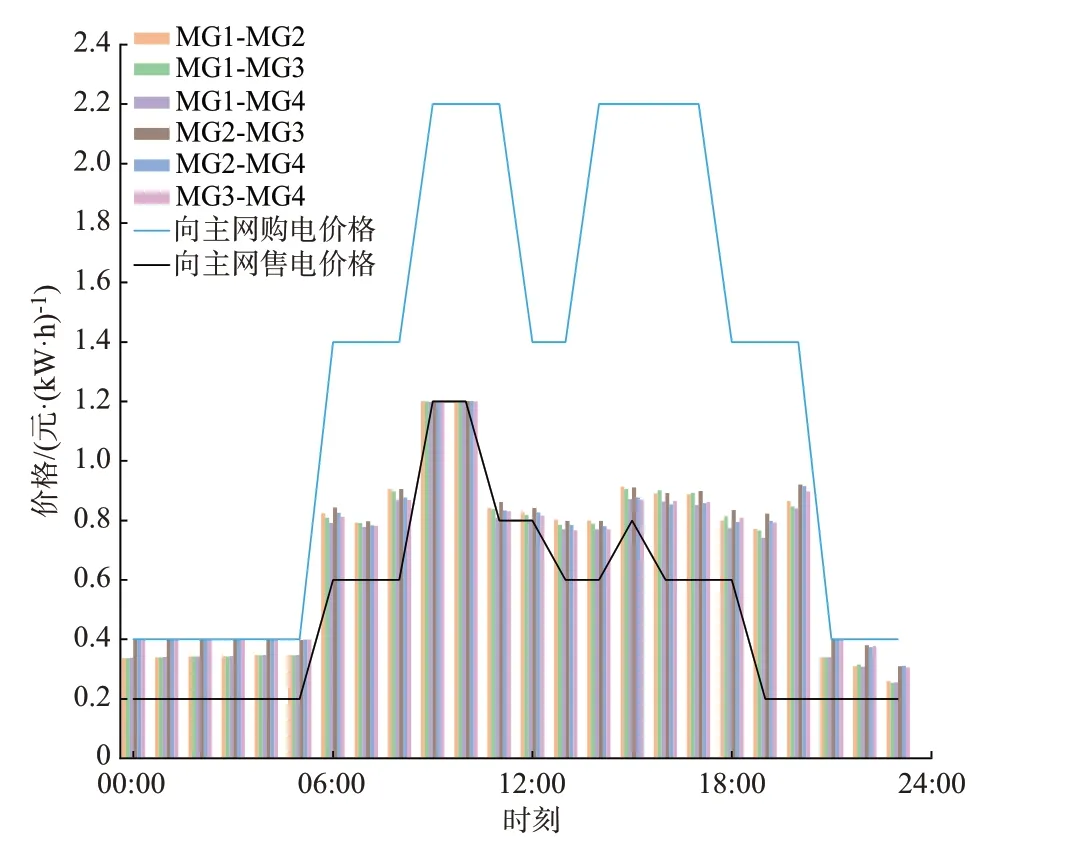
图4 各微网内部及其与主网之间的购售电价格Fig.4 Purchase and sale price within each microgrid and between each microgrid and main grid

为分析交易电价与能量的关系,将MG1 向其他微网输送功率的情况展示如附录E 图E7 所示。MG2、MG3、MG4 夜 间 存 在 电 力 缺 额,故MG1 在00:00—04:00 期间有着相当的定价权,此时交易价格基本由MG1 的边际成本决定,出现MG1 与其他微网交易电能及价格趋同的结果。09:00—10:00期间的定价与向电网售电价格几乎一致,此时MG1基本不进行交易,各微网与上层电网交易即可保证功率平衡,无需多余交易。最终的交易电价总体遵循以下原则:售电方边际售电成本(边际产电成本加上边际税费)等于其售电边际收益(电价),购电方边际产电成本等于其购电边际成本(电价加上边际税费)。各主体内部产电成本的不同也就产生了“价格歧视”现象,这也反映了交易双方的供求关系。
4.3 不同机制下的对比分析
为探讨交易机制及引入潮流约束对各主体成本及总体福利的影响,本文对3 种场景进行仿真分析:1)取消微网间联络线,不进行产消者交易(记为场景1);2)保留交易机制,忽略潮流约束(记为场景2);3)进行集中式优化(记为场景3)。所得结果如表1所示,可见本文机制(记为场景4)相比于无交易,总成本明显下降,这验证了引入交易机制对于社会福利的改善。本文机制与集中式优化结果基本一致,可实现社会福利最大化。而相较于无潮流约束,本文机制由于潮流的限制,成本有所提升,但可有效保证结果的可行性。附录E 图E8 对比了有无潮流约束下6 条联络线4-8、4-12、4-16、8-12、8-16 及12-16的中点电压。由附录E 图E8(a)可见,无潮流约束下的结果存在着电压不匹配的情况。在10 kV 电压等级电网中,不同微网计算所得联络线电压差值最大可达0.586 kV,这种交易在没有大量无功设备支持时是无效的。由附录E 图E8(b)可见,本文机制下各联络线最大电压差值仅为0.027 8 kV。当存在一定无功补偿装置时,这样的电压偏差几乎可以忽略不计。本文机制合理考虑了物理约束,在保证完全分布式交易的同时避免了交易不可行的结果。
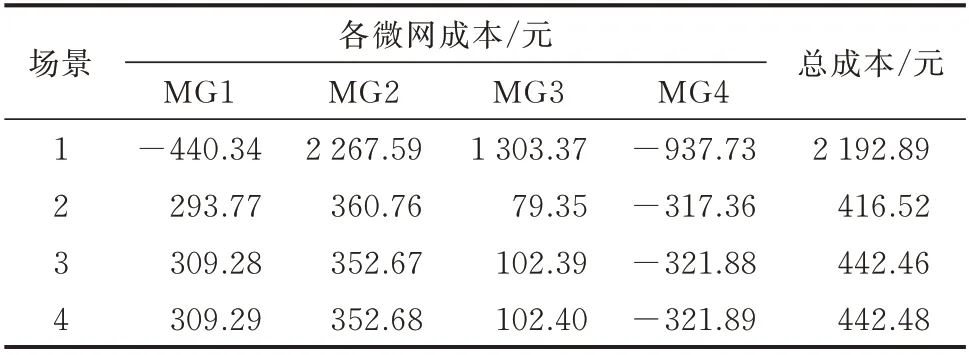
表1 不同场景下各微网成本Table 1 Cost of each microgrid in different scenarios
4.4 交易规模扩展下收敛速度分析
对2 至10 个微网交易的情景进行分析,探究交易规模扩大时迭代的收敛速度。如图5 所示,随交易规模扩大迭代收敛时间增多,但尚可满足日前交易需求。实际上,文献[22]已利用强化学习对加快收敛进行了探讨,这也是今后需要深化研究的方向。
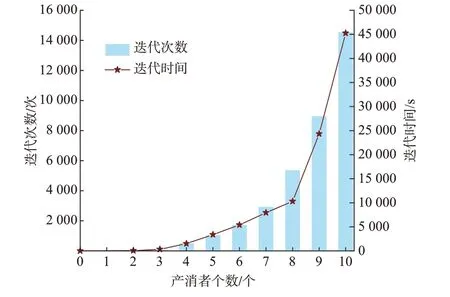
图5 不同规模的产消者所需迭代次数及时间Fig.5 Number and time of iterations required for prosumers with different sizes
5 结语
本文以多微网为例,提出一种多产消者端到端交易机制。该机制充分激发了各主体参与能量交易的积极性,促进了分布式资源就地消纳,实现了资源的有效利用,发挥了各主体内部资源的灵活性,平抑了电网峰谷差。
1)设计了一种考虑物理约束的完全分布式端到端能量交易机制。该机制考虑产消者内部网络约束,引入支路撕裂法及拉格朗日对偶分解法实现主体解耦,基于ADMM 建立交易框架。在有效利用分布式资源的同时,确保了交易结果的可行性。
2)实现无协调主体下多产消者的完全端到端交易运行。本文交易框架不再依赖第三方主体,仅需在交易主体间进行信息交换即可实现端到端交易,且迭代的收敛性与最优性可保证。
3)在产消者交易过程中引入“价格歧视”的概念。通过数学分析,确定对偶乘子与交易电价的等价性。同时,引入“价格歧视”的概念进行分析,说明了本文机制能反映交易主体最大化自身利益的诉求,符合客观的经济学规律。
本文完成了日前多产消者交易机制的讨论。而在新能源的高度渗透下,电网的实时运行充满随机性,且储能的存在使得各时间断面的决策对后续运行有着重要影响,即各主体的决策具有很强的时间耦合性。因此,多产消者日内交易运行是一个具有高度随机性的序贯决策问题,如何设计这种复杂条件下的日内交易机制是未来研究的重要方向。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
