不同释放程度下下肢动脉支架的疲劳强度及寿命预测
2023-02-24马双全冯海全陈彦龙冯浩翔
马双全,冯海全,陈彦龙,冯浩翔
不同释放程度下下肢动脉支架的疲劳强度及寿命预测
马双全1,冯海全1,陈彦龙1,冯浩翔2
(1.内蒙古工业大学 机械工程学院,呼和浩特 010051;2.南京航空航天大学 材料科学与技术学院,南京 210000)
探究释放程度和支架结构对支架疲劳寿命的影响。利用有限元法分析3款镍钛合金下肢动脉支架(Complete SE、E–luminexx–B和Pulsar–35)在脉动载荷作用下的力学性能,基于疲劳应变理论评估支架的疲劳强度,使用Fe–safe和Abaqus软件预测支架在不同释放程度(80%、85%、90%)下的疲劳寿命及安全性。应用Origin软件对支架应力与疲劳寿命进行拟合。支架在释放尺度为80%~90%下的疲劳强度均满足10年疲劳寿命的要求。3种支架释放程度为90%时,疲劳强度大,寿命长;释放程度为80%时,疲劳强度、寿命及安全系数小。相同释放程度下,偏置型波峰结构支架变形后的交变应变及弹性应力值最大,支架寿命及安全系数最小;对称型波峰结构支架CE的寿命及安全系数小于EB。通过LangevinMod函数拟合PR支架疲劳寿命,拟合优度2>0.99。随着释放程度的增大,3款支架疲劳强度、寿命及安全系数呈增大趋势。在相同释放程度下,支撑单元对称型波峰结构支架疲劳强度、寿命及安全系数比偏置型波峰结构支架大,减小对称型波峰结构支架的连接体宽度有利于提高支架寿命。
下肢动脉支架;有限元法;疲劳寿命;安全系数;应力
外周动脉疾病(Peripheral Arterial Diease,PAD)是由于下肢动脉粥样硬化阻塞导致下肢血流量减少所引起的一种下肢动脉疾病[1],有着较高的病发率和死亡率,严重降低了患者的生活质量[2]。血管介入治疗具有微创性、恢复时间短的优点,目前已广泛用于治疗血管类疾病。
临床上发现患者血管直径略有不同[3-4],支架的力学性能会因释放程度的变化而改变,当支架植入血管后,长期受到血流的循环作用[5-6],在血液周期性脉动载荷的作用下,不同释放程度的支架疲劳强度和寿命会出现差异,这对患者的生命安全有重大影响。相关学者研究发现,支架的结构、材料及肢体的生理变形对下肢动脉支架的疲劳寿命有显著影响[7-9]。张瑞敏等[10]揭示了不锈钢血管支架的支撑体长度和宽度对支架疲劳寿命的影响规律。李治国等[11]发现连接体长度对支架疲劳寿命有较大影响。以上研究表明,支架结构及材料会影响支架的疲劳寿命,但对于支架在不同释放程度下的疲劳性能及寿命预测的研究报道较少。
文中选用临床应用广泛且具有代表性的3款下肢动脉支架,建立有限元模型,使用有限元分析软件Abaqus 2019(Dassault Systemes Inc.,法国)及Fe–safe 2019(Dassault Systemes Inc.,法国)模拟分析支架在血管内脉动的疲劳强度,计算不同释放程度下支架的疲劳寿命,为评价支架安全性和可靠性提供参考依据。
1 模型建立与方法
1.1 几何模型
选用已上市的3款下肢动脉支架:Complete SE(Medtronic,美国)、E–luminexx–B(Bard,美国)和Pulsar–35(Biotronik,德国),分别简称为CE、EB、PR,应用三维建模软件solidworks 2016(Dassault Systemes Inc.,法国)建立几何模型,如图1所示。支架结构均由花冠、支撑单元和连接体组成,Complete SE和E–luminexx–B支架支撑单元波峰结构相同,连接体宽度不同,而E–luminexx–B和Pulsar–35支架连接体宽度相似,支撑单元波峰结构不同。模型初始长度为30 mm,直径为6 mm,支架结构尺寸根据样品实际测量获得,均与原产品相同,支架的主要结构参数见表1。
下肢动脉血管壁由3层组成[12],分别为外膜、中膜、内膜,其厚度分别为0.1、0.25、0.15 mm[13],长度为50 mm。支架释放程度为80%、85%、90%的血管直径分别为4.8、5.1、5.4 mm。
1.2 材料属性
基于Abaqus 2019内嵌的材料本构模型对镍钛超弹性合金的材料进行赋予,建立长度为100 mm、直径为1 mm的圆柱体有限元模型,网格划分选用C3D8单元类型。使用Abaqus的Mesh模块以近似全局大小为2.5对网格进行划分,对划分后的模型施加位移约束,对=0的平面施加对称边界条件,约束其自由度,分别对单轴模型的、平面施加对称边界条件,在=100的平面施加轴向位移载荷而后卸载为0。将模拟出的结果与De Bock等[14]实验研究结果进行对比,如图2所示。
镍钛合金的材料属性为[15]:奥氏体弹性模量35 850 MPa,奥氏体泊松比0.3,马氏体弹性模量13 950 MPa,转变应变0.053 2,加载平台开始应力480 MPa,加载平台结束应力640 MPa,卸载平台开始应力270 MPa,卸载平台结束应力200 MPa,压缩平台开始应力480 MPa,奥氏体结束温度283.15 K。

图1 下肢动脉支架的3D模型与实物图
表1 支架主要结构参数

Tab.1 Main structural parameters of stents
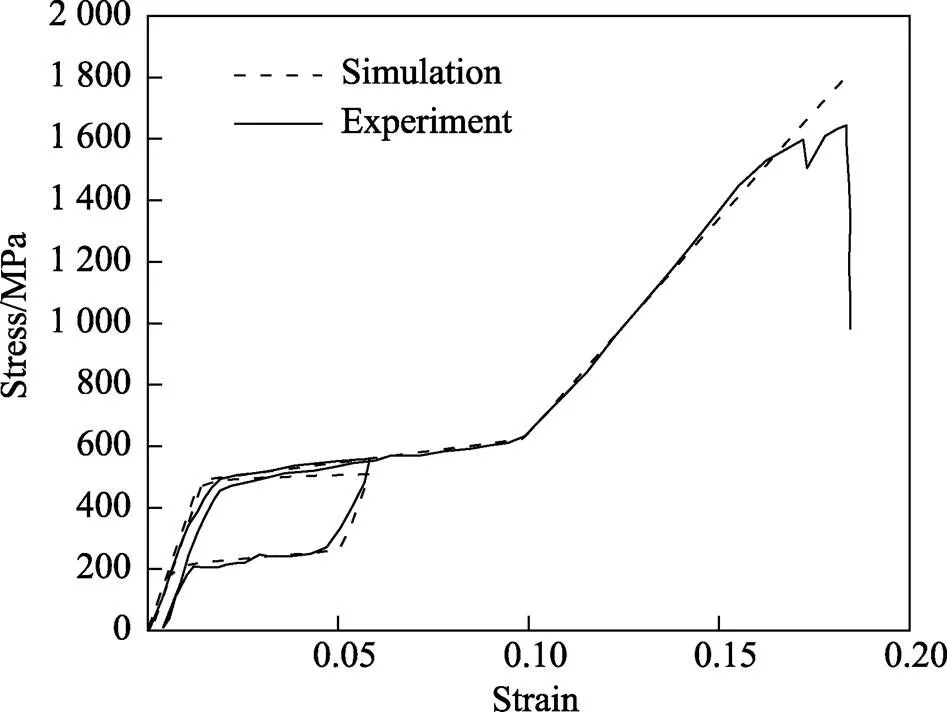
图2 镍钛合金单轴拉伸实验数据与模拟结果
动脉壁的材料常数[16]如表2所示。
表2 血管材料属性

Tab.2 Vascular material properties
Note:10,1,2andare temperature-dependent material parameters, while1and2are vascular fiber directions.
根据文献[17]可知,压握壳密度为6 300 kg/m3,弹性模量为3×108Pa,泊松比为0.499。
1.3 网格划分
对Complete SE支架的轴向1/6模型进行网格灵敏度分析,在支架宽度与厚度表面设计了6种网格密度,分别是2×2、2×4、4×2、4×4、4×6、4×8,将6种网格密度的支架释放到血管内径为5.4 mm的血管内,统计6种支架网格在压握、释放时的应力与计算时间,结果如图3所示。

图3 不同网格密度支架在压握、释放后的最大应力及计算时间
从图3中得出,支架在不同网格密度下压握、释放时的应力相差较大,当支架网格稀疏时,其压握、释放的计算结果较网格密集时偏大,随着网格密度的增大,支架压握、释放后结果相差不大。在仿真计算时,计算时间是不可忽视的因素,网格稀疏时,支架计算时间较少,仿真精度较低;网格密集时,计算时间比稀疏网格长,随着网格密度的增大,计算时间也随之增长。考虑仿真精度与计算时间的平衡,本次仿真模拟支架网格密度选择4×4,支架的网格划分详见表3。
表3 网格模型划分

Tab.3 Mesh model division
1.4 边界条件
将3款支架、压握壳及血管模型分别导入有限元分析软件Abaqus中,对支架、压握壳、血管进行装配,然后对压握壳施加径向位移约束,将支架压握至3 mm,撤掉压握壳,使支架分别以80%、85%、90%的释放程度释放到直径为4.8、5.1、5.4 mm的血管中,在释放后的支架内表面施加交替变化的作用力来模拟人体血管内的脉动循环载荷[18]。使用P表示血管脉动,P–80表示支架以80%的释放程度释放在4.8 mm血管直径内,其余释放程度以此类推。为满足支架具有10年疲劳寿命的要求,根据正常人体内的血压情况,利用有限元法模拟支架承受脉动载荷,极值为80、160 mmHg[19],分别对应压力值0.010 6、0.021 3 MPa,计算完成后,将支架应力应变文件导入到Fe–safe 2019中,分析支架在脉动载荷作用下的寿命与安全系数。
1.5 评价方法
根据美国FDA规定[20],血管支架应该能承受至少4亿次的脉动循环载荷,即满足10年的疲劳寿命要求。目前对于医用镍钛合金自膨胀支架的评价多采用应变检测疲劳[21-22],Pelton等[23]提出了10年为期的107次循环加载–卸载的疲劳寿命极限曲线,即与0.4%交变应变振幅对应的线作比较,根据其提出的一种专门针对镍钛合金材料的疲劳强度评价方法,将计算后支架所有节点的最大和最小弹性应变结果导入Excel 2019中,支架所有单元的应变幅和平均应变分别应用式(2)和式(3)[24]计算得到。

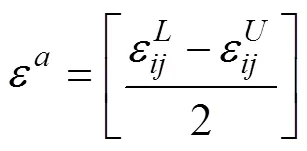
理论上,支架在血管内的脉动次数超过4×108次,为超高周疲劳分析,文中使用名义应力法对支架进行寿命计算,以保证支架在服役过程中的安全性。使用Fe–safe 2019计算支架寿命。基于Abaqus有限元分析结果,根据相关文献拟合得到镍钛合金材料的标准试件在平均应力为零时的S–N曲线[25],使用正弦曲线载荷谱,频率为60 Hz。使用Abaqus和Fe–safe对支架的疲劳寿命和安全系数进行计算。
2 结果与分析
2.1 疲劳强度
3款支架在不同释放程度下的疲劳极限如图4所示。CE–80%表示Complete SE支架以80%释放程度释放到直径4.8 mm的血管内,其他编号以此类推。结果显示,在不同释放程度下,3款支架所有节点的交变应变均处于疲劳极限下方,说明支架在承受脉动载荷时满足10年疲劳寿命要求。PR支架在不同释放程度下释放的疲劳强度有所不同,释放程度90%时其疲劳强度较大,释放程度80%时疲劳强度较小,其他2款支架疲劳强度规律与PR支架相同,随着释放程度的增大,3款支架疲劳强度均呈增大趋势。在释放程度为80%时,PR支架的疲劳强度较小,EB支架疲劳强度较大,从结构分析,PR支架的支撑单元波峰结构是偏置型,偏置型波峰结构支架变形时,支撑体夹角变化量较大,则支架交变应变值较大,而其他支架的支撑单元波峰结构是对称型,支撑体夹角变化量较小,交变应变值较小。因此,支撑单元结构对支架疲劳强度影响较大。
2.2 疲劳寿命与安全系数
图5是3款支架在不同释放程度下的等效应力分布云图。3款支架以3种释放程度释放的最大等效应力均位于支架圆弧内侧且主要集中在端部连接筋内侧,此处易发生疲劳失效。这是由于3款支架的端部结构为闭环结构,中间部位为开环结构,闭环结构比开环结构的约束多,变形时易引起应力集中现象。释放程度为80%时,CE、EB、PR支架的应力值分别为125.2、91.09、173.6 MPa,PR支架等效应力最大,从结构分析,PR支架的支撑单元波峰结构是偏置型,偏置型波峰结构支架变形时,支撑体夹角变化量较大,则支架支撑体最大等效应力较大,而其他支架的支撑单元波峰结构是对称型,支撑体夹角变化量较小,即支架支撑体最大等效应力较小,因此,支架结构对最大等效应力有显著影响。PR支架在释放程度为80%、85%、90%时对应的最大等效应力分别为173.6、115.4、70.56 MPa,说明随着释放程度的增大,支架最大等效应力呈减小趋势,其他2款支架最大等效应力趋势与PR支架相同。

图4 支架疲劳强度的极限应变线图
支架在不同释放程度下的最大等效应力、疲劳寿命和安全系数如图6所示。结果显示,3款支架的最大等效应力与疲劳寿命和安全系数成反比,疲劳寿命与安全系数成正比。脉动载荷下,CE支架释放程度为80%、85%、90%时,其对应的理论寿命分别为17.76、25.72、28.77年,安全系数分别为1.538、2.148、2.512;EB支架在3种释放程度下的理论寿命分别为22.83、27.85、30.47年,安全系数分别为1.915、2.389、2.656;PR支架在3种释放程度下的理论寿命分别为11.36、19.08、26.5年,安全系数分别为1.055、1.655、2.203,说明随着释放程度的增大,支架疲劳寿命及安全系数呈增大趋势。释放程度为80%时,CE、EB、PR支架寿命分别为17.76、22.83、11.36年,安全系数分别为1.538、1.915、1.055,可以看出,EB支架寿命及安全系数最大,PR支架寿命及安全系数最小,因支撑单元对称型波峰结构最大等效应力小于偏置型波峰结构,则EB支架疲劳寿命较大,说明对称型波峰结构有利于提高支架的疲劳寿命。对称型波峰结构支架中,CE支架的寿命小于EB支架,从结构上看,CE支架的连接体宽度大于EB支架,连接体宽度越大,支架最大等效应力越大,因此,减小连接体宽度有利于提高支架寿命。这里未考虑支架腐蚀,以及血管弯曲、斑块大小和硬度的影响,故此支架实际寿命值应低于上述分析结果。然而,文中研究能够表明,支架结构及释放程度对支架寿命有显著影响。
PR支架在脉动载荷下的疲劳寿命曲线如图7所示。可以看出,随着等效应力的减小,疲劳寿命呈增长趋势。使用Origin 2019指数拟合函数对支架疲劳寿命进行拟合。通过Asymptotic1、Chapman、LangevinMod函数模型拟合,发现LangevinMod函数模型拟合效果最好,拟合优度2>0.99,该函数优化算法如式(3)所示。
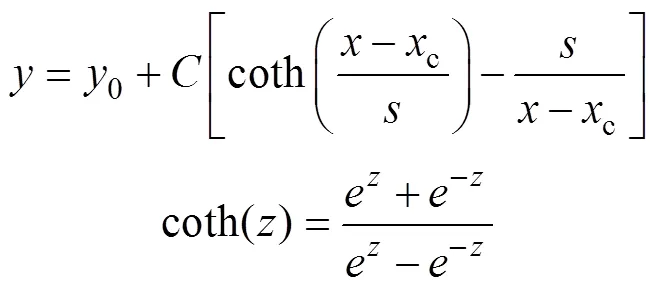
式中:y0为偏移量;c为幅值;xc为尺度修正中心;s为比例大小。

图6 3种释放程度下支架的应力、寿命与安全系数

图7 支架在脉动载荷下的疲劳寿命拟合
3 结论
利用有限元分析方法研究了下肢动脉支架在不同释放程度下的疲劳强度,并对其进行了寿命预测,得到以下主要结论。
1)经疲劳强度分析发现,随着释放程度的增大,3款支架疲劳强度呈增大趋势。支撑单元对称型波峰结构支架疲劳强度比偏置型波峰结构支架大。
2)通过支架寿命预测发现,随着释放程度的增大,3款支架疲劳寿命及安全系数呈增大趋势。相同释放程度下,对称型波峰结构支架寿命及安全系数大于偏置型结构支架,减小对称型波峰结构支架的连接体宽度有利于提高支架寿命及安全系数。
3)通过LangevinMod函数拟合PR支架疲劳寿命,拟合优度2>0.99,回归直线对寿命计算值拟合良好,为血管支架设计及优化提供了参考。
[1] ANSARI F, PACK L K, BROOKS S S, et al. Design Considerations for Studies of the Biomechanical Environment of the Femoropopliteal Arteries[J]. Journal of Vascular Surgery, 2013, 58(3): 804-813.
[2] FOWKES F G R, RUDAN D, RUDAN I, et al. Comparison of Global Estimates of Prevalence and Risk Factors for Peripheral Artery Disease in 2000 and 2010: A Systematic Review and Analysis[J]. The Lancet, 2013, 382(9901): 1329-1340.
[3] FENG Hai-quan, GUO Fei-fei, JIANG Xu-dong, et al. Research on the Coupling Expansion Mechanism of Balloon-Expandable Coronary Stent[M]//Advances in Intelligent and Soft Computing. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 585-590.
[4] 张站柱, 乔爱科, 付文宇. 不同连接筋结构的支架治疗椎动脉狭窄的血流动力学数值模拟[J]. 医用生物力学, 2013, 28(2): 148-153.
ZHANG Zhan-zhu, QIAO Ai-ke, FU Wen-yu. Hemodynamic Simulation of Vertebral Artery Stenosis Treated by Stents with Different Links[J]. Journal of Medical Biomechanics, 2013, 28(2): 148-153.
[5] 陈宇, 王冠石, 陈冲, 等. 生物可降解聚合物支架构型设计与力学性能研究[J]. 生物医学工程学杂志, 2020, 37(6): 967-973.
CHEN Yu, WANG Guan-shi, CHEN Chong, et al. Design and Mechanical Properties of Biodegradable Polymeric Stent[J]. Journal of Biomedical Engineering, 2020, 37(6): 967-973.
[6] 彭坤, 李婧, 王斯睿, 等. 可降解血管支架结构设计及优化的研究进展[J]. 中国生物医学工程学报, 2019, 38(3): 367-374.
PENG Kun, LI Jing, WANG Si-rui, et al. Research Progress on the Structure Design and Optimization of Biodegradable Stents[J]. Chinese Journal of Biomedical Engineering, 2019, 38(3): 367-374.
[7] LEI Long, QI Xiao-zhi, LI Shi-bo, et al. Finite Element Analysis for Fatigue Behaviour of a Self-Expanding Nitinol Peripheral Stent under Physiological Biomechanical Conditions[J]. Computers in Biology and Medicine, 2019, 104: 205-214.
[8] MEOLI A, DORDONI E, PETRINI L, et al. Computational Study of Axial Fatigue for Peripheral Nitinol Stents[J]. Journal of Materials Engineering and Performance, 2014, 23(7): 2606-2613.
[9] 杨练, 段焕玲. 镍钛合金支架疲劳性能的研究进展[J]. 硬质合金, 2021, 38(6): 454-459.
YANG Lian, DUAN Huan-ling. Research Progress on Fatigue Performance of Nitinol Alloy Stents[J]. Cemented Carbide, 2021, 38(6): 454-459.
[10] 张瑞敏. 基于Abaqus的血管内支架疲劳强度分析[D]. 呼和浩特: 内蒙古工业大学, 2014.
ZHANG Rui-min. Fatigue Strength Analysis of Vascular Stent Based on Abaqus[D]. Hohhot: Inner Mongolia University of Tehchnology, 2014.
[11] 李治国, 冯海全, 闫文刚. 颅内动脉支架的疲劳强度[J]. 医用生物力学, 2018, 33(5): 442-446.
LI Zhi-guo, FENG Hai-quan, YAN Wen-gang. Fatigue Strength for Intracranial Artery Stents[J]. Journal of Medical Biomechanics, 2018, 33(5): 442-446.
[12] HOLZAPFEL G A, STADLER M, SCHULZE-BAUER C A. A Layer-Specific Three-Dimensional Model for the Simulation of Balloon Angioplasty Using Magnetic Resonance Imaging and Mechanical Testing[J]. Annals of Biomedical Engineering, 2002, 30(6): 753-767.
[13] STARY H C, BLANKENHORN D H, CHANDLER A B, et al. A Definition of the Intima of Human Arteries and of Its Atherosclerosis-Prone Regions. A Report from the Committee on Vascular Lesions of the Council on Arteriosclerosis, American Heart Association[J]. Arteriosclerosis and Thrombosis: a Journal of Vascular Biology, 1992, 12(1): 120-134.
[14] DE BOCK S, IANNACCONE F, DE SANTIS G, et al. Virtual Evaluation of Stent Graft Deployment: A Validated Modeling and Simulation Study[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2012, 13: 129-139.
[15] GÖKGÖL C, DIEHM N, NEZAMI F R, et al. Nitinol Stent Oversizing in Patients Undergoing Popliteal Artery Revascularization: A Finite Element Study[J]. Annals of Biomedical Engineering, 2015, 43(12): 2868-2880.
[16] GASSER T C, OGDEN R W, HOLZAPFEL G A. Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations[J]. Journal of the Royal Society, Interface, 2006, 3(6): 15-35.
[17] 赵振心, 刘道志, 孙康, 等. 镍钛合金血管支架的有限元分析及疲劳测试[J]. 中国医疗器械杂志, 2008, 32(5): 373-376.
ZHAO Zhen-xin, LIU Dao-zhi, SUN Kang, et al. Finite Element Analysis and Fatigue Tests for Nitinol Vascular Stents[J]. Chinese Journal of Medical Instrumentation, 2008, 32(5): 373-376.
[18] 张宏辉, 冯海全, 李治国, 等. 镁合金冠脉支架支撑性能分析及其优化[J]. 医用生物力学, 2019, 34(1): 14-20.
ZHANG Hong-hui, FENG Hai-quan, LI Zhi-guo, et al. Analysis and Optimization for Support Performance of Magnesium Alloy Stent[J]. Journal of Medical Biomechanics, 2019, 34(1): 14-20.
[19] 冯海全, 张瑞敏, 韩青松, 等. 血管内支架的疲劳强度的有限元模拟分析[J]. 功能材料, 2014, 45(14): 14087-14091, 14098.
FENG Hai-quan, ZHANG Rui-min, HAN Qing-song, et al. Finite Element Analysis of Fatigue Strength of Vascular Stent[J]. Journal of Functional Materials, 2014, 45(14): 14087-14091, 14098.
[20] FOR Q P, TOOLS D D. Guidance for Industry and FDA Staff[M]//Handbook of Adhesives and Surface Preparation. Amsterdam: Elsevier, 2011: 395-405.
[21] 王硕, 汤京龙, 陆颂芳, 等. 冠状动脉支架耐疲劳评价体系的研究[J]. 中国药事, 2009, 23(9): 881-883.
WANG Shuo, TANG Jing-long, LU Song-fang, et al. Study on the Evaluation Systems of Coronary Stents after Long Term Accelerating Fatigue Test in Vitro[J]. Chinese Pharmaceutical Affairs, 2009, 23(9): 881-883.
[22] SENTHILNATHAN K, SHAMIMI A, BONSIGNORE C, et al. Effect of Prestrain on the Fatigue Life of Superelastic Nitinol[J]. Journal of Materials Engineering and Performance, 2019, 28(10): 5946-5958.
[23] PELTON A R, GONG X Y, DUERIG T. Fatigue Testing of Diamond-Shaped Specimens[J]. Medical Device Materials, 2003: 199-204.
[24] 王天琪, 冯海全, 王坤. 下肢动脉支架在多种变形模式下的力学性能对比研究[J]. 生物医学工程学杂志, 2021, 38(2): 303-309.
WANG Tian-qi, FENG Hai-quan, WANG Kun. Comparative Study on the Mechanical Properties of Lower Limb Arterial Stents under Various Deformation Modes[J]. Journal of Biomedical Engineering, 2021, 38(2): 303-309.
[25] 智友海, 史向平. NiTi心血管支架的疲劳断裂性能分析[J]. 医用生物力学, 2011, 26(1): 1-6.
ZHI You-hai, SHI Xiang-ping. Fatigue and Fracture Behavior of Nitinol Cardiovascular Stents[J]. Journal of Medical Biomechanics, 2011, 26(1): 1-6.
Fatigue Strength and Life Prediction of Lower Extremity Arterial Stents under Different Release Degrees
MA Shuang-quan1, FENG Hai-quan1, CHEN Yan-long1, FENG Hao-xiang2
(1. College of Mechanical Engineering, Inner Mongolia University of Technology, Hohhot 010051, China; 2. College of Material Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 210000, China)
The work aims to explore the effects of release degree and structure on fatigue life of stents. The mechanical properties of three Nitinol lower extremity arterial stents (Complete SE, E-luminexx-B and Pulsar-35) under pulsating load were analyzed by the finite element method. The fatigue strength of stents was evaluated based on the fatigue strain theory. Fe-safe and Abaqus software were used to predict the fatigue life and safety of stents under different release degrees (80%, 85% and 90%). Origin software was used to fit the stress and fatigue life of the stents. The fatigue strength of the stents at the release degree of 80%-90% met the fatigue life requirement of 10 years. When the release degree of the three stents was 90%, the fatigue strength was high and the service life was long; while the release degree was 80%, the fatigue strength, life and safety coefficient were small. Under the same release degree, the alternating strain and elastic stress of the skewed wave crest structure were the largest, and the life and safety coefficient of the stents were the smallest. The life and safety coefficient of the symmetrical crest structure stent CE were less than those of EB. The fatigue life of PR stent was fitted by LangevinMod function, and the goodness of fit2was >0.99. With the increase of the release degree, the fatigue strength, life and safety coefficient of the three stents increase. Under the same release degree, the fatigue strength, life and safety coefficient of the symmetric wave crest structure of the stent element are larger than those of the offset wave crest structure. Reducing the width of the connecting body of the symmetric wave crest structure is beneficial to improve the life of the stents.
lower extremity arterial stent; finite element method; fatigue life; safety coefficient; stress
10.3969/j.issn.1674-6457.2023.02.004
O343.8;O346.23
A
1674-6457(2023)02-0029-08
2022–09–29
2022-09-29
国家自然科学基金(12162026);内蒙古自治区科技计划(2020GG0024)
National Natural Science Foundation of China (12162026); Inner Mongolia Science and Technology Project (2020GG0024)
马双全(1995—),男,硕士生,主要研究方向为介入医疗器械优化设计及可靠性评价。
MA Shuang-quan (1995-), Male, Postgraduate, Research focus: optimal design and reliability evaluation of interventional medical devices.
冯海全(1972—),男,博士,教授,主要研究方向为微小机械设计及理论、介入医疗器械研发。
FENG Hai-quan (1972-), Male, Doctor, Professor, Research focus: design and theory of micro machinery and research, and development of interventional medical devices.
马双全, 冯海全, 陈彦龙, 等. 不同释放程度下下肢动脉支架的疲劳强度及寿命预测[J]. 精密成形工程, 2023, 15(2): 29-36.
MA Shuang-quan, FENG Hai-quan, CHEN Yan-long, et al. Fatigue Strength and Life Prediction of Lower Extremity Arterial Stents under Different Release Degrees[J]. Journal of Netshape Forming Engineering, 2023, 15(2): 29-36.
