基于BP神经网络算法的316L不锈钢极薄带热处理力学性能预测
2023-02-24张志雄付永伟王涛王彬熊晓燕王天翔
张志雄,付永伟,王涛,王彬,熊晓燕,王天翔
钢铁成形
基于BP神经网络算法的316L不锈钢极薄带热处理力学性能预测
张志雄1a,1b,付永伟1a,王涛1a,1b,王彬1b,熊晓燕1a,王天翔2
(1.太原理工大学 a.机械与运载工程学院 b.先进金属复合材料成形技术与装备教育部工程研究中心,太原 030024;2.山西太钢不锈钢精密带钢有限公司,太原 030006)
为了预测不锈钢极薄带热处理后的力学性能、优化热处理工艺以及实现热处理工艺的智能控制,构建基于BP算法的神经网络模型。以316L不锈钢极薄带为研究对象,进行热处理试验和拉伸试验,通过以热处理的退火温度、保温时间和取样方向作为输入层参数,以屈服强度、抗拉强度、断后伸长率作为输出层参数,采用BP算法构建了316L不锈钢极薄带力学性能预测的思维进化算法优化BP神经网络模型,并进行模型的预测和应用验证,考虑不同隐含层节点数及不同BP神经网络模型对性能的影响。思维进化算法优化的BP神经网络模型测试集的屈服强度、抗拉强度和断后伸长率的平均相对误差分别为8.92%、5.21%和9.28%,训练集相关系数为0.980 94。思维进化算法优化BP网络单、双隐含层误差总和最低分别为0.578 6和0.546 9,BP网络与思维进化算法优化的BP网络误差总和最低分别为0.579 9和0.546 9。思维进化算法优化BP神经网络模型具有较好的预测能力和泛化能力,以及较高的预测精度。与企业现用生产工艺相比,采用模型优化后热处理工艺的综合力学性能有显著提高。
BP神经网络;思维进化算法(MEA);316L;极薄带;热处理;综合量化
强度和塑性是衡量金属材料力学性能的重要指标,这两种性能不足是引起材料失效的主要原因。随着现代科技的突飞猛进,新产品呈现出微型化的发展趋势,不锈钢具有耐腐蚀、美观、成本低等诸多优点,使得不锈钢极薄带的应用日益广泛。不锈钢极薄带广泛应用于航空航天、电子设备、医疗设备、汽车制造、能源设备等诸多领域,如卷簧、屏幕基底、电池包覆材料、手机震动器、眼镜框架[1-3],对不锈钢极薄带的力学性能提出了更高的要求。不锈钢极薄带主要通过轧制来成形,但在轧制过程中伴随着材料内部组织、结构及性能的变化[4]。为了改善不锈钢极薄带的服役性能,需要对其进行热处理,但是热处理工艺参数众多且相互影响,目前不锈钢极薄带热处理后力学性能的控制主要依靠经验公式或试验手段进行,对力学性能的需求变化缺乏适应性,无法实现智能控制的要求。
近年来,神经网络已经用于解决工程中一些复杂的非线性问题,应用最多的是BP神经网络。在实际应用中,约有80%的神经网络模型采用了BP神经网络或BP神经网络的变化形式[5]。BP神经网络是采用误差反向传播算法训练的多层前馈神经网络,是处理输入与输出之间复杂非线性问题的有效方法[6-8]。李志峰等[9]采用BP神经网络对影响冷轧不锈钢表面硬度的因素进行了分析,并建立了模型对硬度进行预测,结果较为准确。路泽永[10]基于BP算法构建了BP神经网络模型,对耐磨钢热处理后的硬度进行了预测和应用验证。张学宾等[11]建立了BP神经网络和粒子群算法优化的BP神经网络模型,对不同线径的Cu-Ag合金微丝抗拉强度进行了预测。
极薄带材在厚度方向会出现单层晶现象,导致其力学性能与宏观尺寸材料有所不同,目前对这方面的研究还较少,利用神经网络对极薄带综合力学性能预测的研究也不足。文中以316L不锈钢极薄带为试验对象,将人工神经网络技术应用于不锈钢极薄带的热处理力学性能预测,建立基于BP算法的思维进化算法(Mind Evolutionary Algorithm,MEA)优化的BP神经网络模型,以期为不锈钢极薄带热处理工艺优化和力学性能预测提供参考。
1 热处理与拉伸试验
1.1 热处理试验
材料:316L不锈钢极薄带,山西太钢不锈钢精密带钢有限公司。仪器:CHY-1700真空管式加热炉,河南成仪设备科技有限公司。方法:以轧制态316L奥氏体不锈钢极薄带为研究对象,带材尺寸为150 mm×45 mm×0.05 mm,取样方向为轧向R和横向T,热处理工艺为固溶处理,退火温度为800~1 050 ℃,保温时间为0.5~5 min。
将极薄带裁剪后,采用包裹法对材料进行防氧化保护,然后放置于通入惰性气体的管式加热炉内保温一定时间,然后出炉空冷。
1.2 拉伸试验
材料:316L不锈钢极薄带。仪器:DK7740T数控中走丝电火花线切割机床,产自泰州市罡阳龙宇机械厂;INSTRON5969电子万能材料试验机,产自美国ITW集团英斯特朗公司。方法:将热处理后的316L极薄带试样用电火花线切割机制成平面尺寸如图1所示的拉伸件,打磨后在INSTRON5969型电子万能材料试验机上进行单向拉伸试验,测试温度为室温,拉伸速率为1 mm/min,试验次数为3。
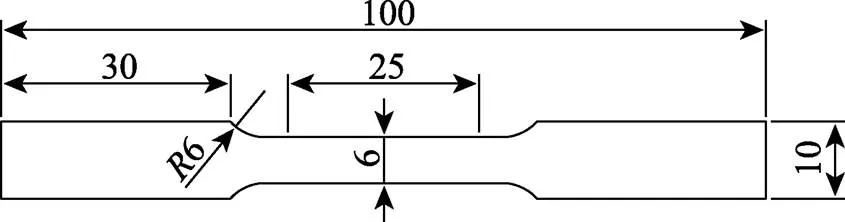
图1 拉伸件尺寸图(单位:mm)
1.3 拉伸试验结果
对上述热处理后的316L极薄带进行室温单向拉伸试验,获得不同热处理条件下的拉伸曲线,随退火温度、保温时间变化的拉伸曲线分别如图2a、b所示,R、T 2个方向的拉伸曲线比较结果如图2c所示。
由图2a可知,随着退火温度的升高,316L奥氏体不锈钢极薄带的屈服强度和抗拉强度逐渐降低,断后伸长率逐渐增大。由图2b可知,随着保温时间的延长,316L不锈钢极薄带的屈服强度和抗拉强度逐渐降低,断后伸长率逐渐增大。由图2c可知,轧制态和退火态的316L不锈钢极薄带具有明显的各向异性,T方向的屈服强度、抗拉强度和断后伸长率均高于R方向。
2 BP神经网络简介
BP神经网络是一种多层前馈神经网络[12-13],由输入层、隐含层和输出层3部分组成,隐含层层数可以是单层或多层,该网络的主要特点是工作信号前向传递,误差信号反向传播,这种沿着误差性能函数梯度反向修改权值的网络称为标准BP神经网络。BP神经网络具有强大的非线性映射能力,广泛应用于分类、拟合、诊断、预测等领域[14-15]。
自20世纪70年代以来,随着遗传学、仿生学和人工智能学科的发展,出现了一系列新的优化算法—智能优化算法,包括进化算法[16-18]和群智能算法[19-20]。进化算法主要通过选择、重组、变异来模拟生物进化过程,实现优化问题的求解,包括遗传算法(Genetic Algorithm,GA)、思维进化算法、模拟退火算法等。群智能算法是基于动物群体协作的随机搜索算法,包括蚁群算法、粒子群算法(Particle Swarm Optimization Algorithm,PSO)等。
其中,遗传算法[21]是借鉴生物适者生存、优胜劣汰的进化规律演化而来的随机搜索算法;粒子群算法[21]是通过模拟鸟群觅食行为发展而来的随机搜索算法;思维进化算法[22-24]是对遗传算法进行借鉴和改进发展而来的随机搜索算法,借鉴了遗传算法“群体”和“进化”的概念,引入“趋同”和“异化”的概念。
标准BP神经网络包括BP神经网络结构确定和BP神经网络预测两部分,智能算法优化BP神经网络包括BP神经网络结构确定、智能算法优化和BP神经网络预测3部分,思维进化算法优化BP神经网络(MEA-BP)是智能算法优化BP神经网络的一种。二者的主要区别在于BP神经网络初始权值、阈值的不同:标准BP神经网络的初始权值和阈值默认为0;智能算法优化BP神经网络的权值和阈值要经过智能算法优化,经过优化后的网络预测精度一般高于未优化的网络。
MEA-BP神经网络的流程图如图3所示,包括BP神经网络结构确定、思维进化算法优化和BP神经网络预测3个部分。

图2 316L不锈钢极薄带拉伸曲线

图3 MEA-BP神经网络流程
3 MEA-BP神经网络模型的建立
3.1 划分数据集
3.1.1 5折交叉验证法
选取156组样本数据,为保证测试集至少包含30个样例,采用5折交叉验证法将数据按4:1的比例随机划分为训练集与测试集。训练集用于更新模型参数,测试集用于表征网络模型的泛化能力。此法用于试错法以确定最佳的隐含层层数及节点数。
3.1.2 留出法
按照与5折交叉验证法相当的留出法对156组样本数据划分数据集,训练集和测试集分别包含126组和30组数据。此法用于最佳BP神经网络模型的训练与测试。
此外,系统默认将训练集分为训练子集、验证子集和测试子集,分别占训练集的75%、15%和15%。训练子集用于训练模型,验证子集用于评估模型、调整参数,测试子集用于测试模型。
3.2 数据预处理
为了统一样本数据,保证训练效果,采用mapminmax函数将样本数据归一化处理到[‒1,1],预测结束后还需进行反归一化。
3.3 BP神经网络结构的确定
在316L奥氏体不锈钢神经网络模型的构建中,需要设计的参数包括网络层数、输入层节点数、隐含层节点数、输出层节点数及传输函数、训练函数、训练参数等。选取热处理的退火温度、保温时间和取样方向作为输入层参数,故输入层节点数为3,各输入节点的取值范围如表1所示。以屈服强度、抗拉强度和断后伸长率为输出层参数,故输出层节点数为3。
表1 输入层节点的取值范围

Tab.1 Value range of input layer nodes
在传输函数的选择上,将tansig函数作为输入层到隐含层的传输函数,隐含层到输出层则选择purelin函数。训练函数选用trainlm函数,LM算法在曲线拟合问题上具有良好的运算速度和运算精度。设置阻尼因子为0.01,采用MSE均方误差来衡量系统性能。此外,为了结束迭代,设置最大训练次数为500,最小MSE均方根误差值为1×10‒4,检查样本的检查值为20。当MSE误差值连续20次不下降或误差值小于1×10‒4或达到最大迭代次数时,结束迭代。
3.4 适应度函数与优化算法参数设置
优化算法都需要一个适应度函数来衡量个体优劣,对个体进行选择。文中选用训练集均方误差的倒数作为适应度函数,适应度值越大的个体越好。表2—4分别为遗传算法、粒子群算法、思维进化算法的初始参数设置。
表2 遗传算法参数设置

Tab.2 GA parameter setting
表3 粒子群算法参数设置

Tab.3 PSO parameter setting
表4 思维进化算法参数设置

Tab.4 MEA parameter setting
3.5 隐含层层数及节点数
隐含层层数及节点数对BP网络性能有很大影响,是神经网络模型构建中比较关键的环节。目前并没有一个理想的解析式可以用来确定合理的隐含层节点数,实际应用中通常依靠试错来调整[5]。文中采用思维进化算法优化BP神经网络、隐含层层数为2、隐含层节点数为[6,14]的模型对316L不锈钢极薄带力学性能进行训练与预测。
4 MEA-BP神经网络结果与讨论
采用拓扑结构为3×6×14×3的思维进化算法优化BP神经网络模型训练,整个思维进化算法迭代过程经过4次“趋同”和3次“异化”,当临时子种群适应度函数值均小于优胜子种群时,迭代过程结束。将最优个体的编码输出,按照编码规则解码后得到最优的BP神经网络初始权值和阈值,然后对测试集进行预测。
4.1 训练性能曲线
图4为MEA-BP神经网络的训练性能曲线。从图4中可以看出,模型经过24次迭代(图中细虚线)后,模型验证子集的均方误差值达到最小值0.026 1,训练子集与测试子集的均方误差值分别为0.008 6和0.017 8。又经过20次迭代,验证子集均方误差值不再减小,迭代过程结束,训练子集、验证子集及测试子集的均方误差值分别为0.007 0、0.029 2和0.015 4。验证子集均方误差值在第7次迭代时增大,随着迭代继续进行,均方差值继续下降;经过44次迭代,均方误差值趋于稳定,说明样本数据训练过程中未出现过多的局部最优现象,模型较为合理稳定。且测试子集均方误差值略大于训练子集,测试子集曲线与验证子集曲线非常相似,说明网络模型拟合状态良好,泛化能力较好。
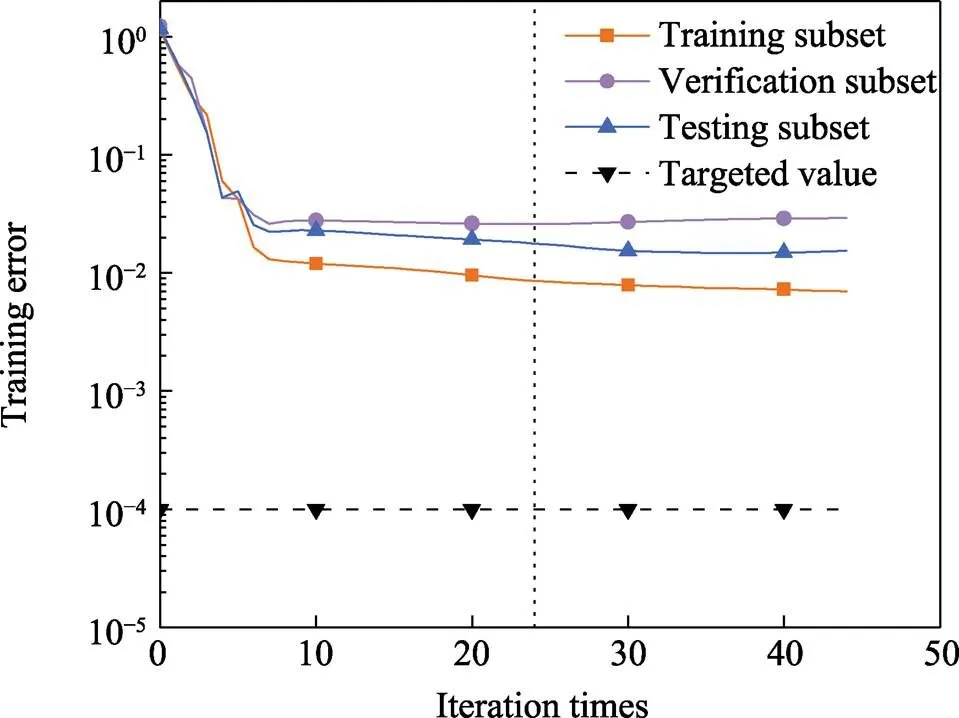
图4 训练性能曲线
4.2 回归能力分析
图5为训练子集、验证子集、测试子集及训练集的回归能力分析图,其中,散点为归一化后的样本数据;蓝色较粗直线表示仿真预测值和真实值之间的最佳拟合线性回归线;虚线表示仿真预测值=真实值;两条红色细线表示虚线的偏置线;偏置线之间包含90%的数据点;值表示仿真值和真实值之间的关系。神经网络训练子集(图5a)、验证子集(图5b)、测试子集(图5c)和训练集(图5d)的相关系数分别为0.986 58、0.967 46、0.973 47和0.980 94,表明屈服强度、抗拉强度和断后伸长率的仿真值与真实值之间有高度的线性正相关关系。偏置值相对较小,表明神经网络模型具有较高的预测精度和良好的泛化能力。
表5为各个子集和训练集的回归直线方程及其斜率和偏置。可见,斜率较为接近1,偏置较为接近0,表明神经网络模型合理,且具有较高的预测精度和良好的泛化能力。
4.3 误差分析
图6显示了训练集与测试集3个输出参数的真实值、仿真值及绝对误差值。可以看出,真实值折线图与仿真值折线图较为吻合,绝对误差值较低,说明MEA-BP神经网络具有较高的预测能力和预测精度。
表6为MEA-BP神经网络测试集部分样本数据的真实值、仿真值及相对误差值。表7为训练集、测试集和数据集总体的平均相对误差。由表6、表7可以看出,测试集真实值与仿真预测值相差较小,相对误差值较小;测试集平均相对误差略大于训练集,说明MEA-BP网络模型具有良好的泛化能力;测试集屈服强度、抗拉强度和断后伸长率的平均相对误差分别为0.089 2、0.052 1和0.092 8,说明预测值与真实值吻合度较高,模型可用。
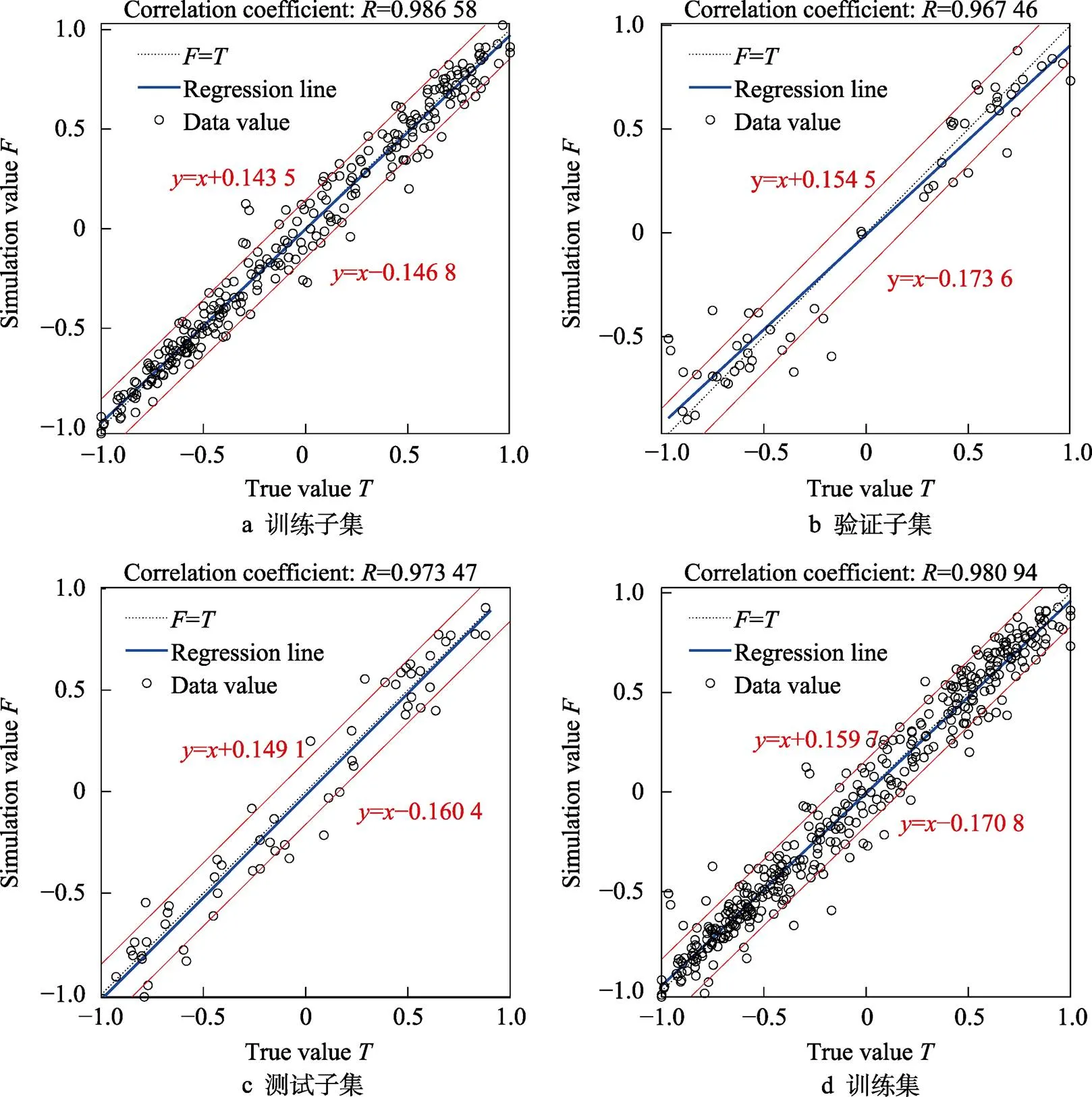
图5 神经网络回归能力分析
表5 回归直线方程

Tab.5 Regression linear equation
由此可见,本研究构建的316L不锈钢极薄带力学性能预测MEA-BP神经网络模型具有较快的收敛速度和较好的稳定性,可以客观反映输入参数(退火温度、保温时间和取样方向)和输出参数(屈服强度、抗拉强度和断后伸长率)之间的关系,在预测性、精确性和泛化性上表现出色,可用于316L不锈钢极薄带退火后力学性能预测。
4.4 不同隐含层层数及节点数性能比较
表8为MEA-BP单、双隐含层神经网络的性能比较,可以看出,双隐含层MEA-BP神经网络具有更低的训练集误差、测试集误差及误差总和,网络性能更好。这是因为网络层数在一定程度上的增加使连接关系更加复杂,可以更好地表征复杂非线性关系。
4.5 不同神经网络模型性能比较
表9为标准BP及3种智能算法优化BP神经网络的性能比较,3种优化算法分别在隐含层节点数为[4,9]、[3,12]和[6,14]时性能达到最好。与标准BP算法相比,智能算法优化BP神经网络的训练集误差都有明显降低;GA-BP算法和PSO-BP算法的测试集误差都有一定增大,MEA-BP算法则明显降低,使得MEA-BP算法在隐含层节点数为[6,14]时误差总和最低,为0.546 9,表明思维进化算法对该问题权值阈值的优化更好,网络性能更好。
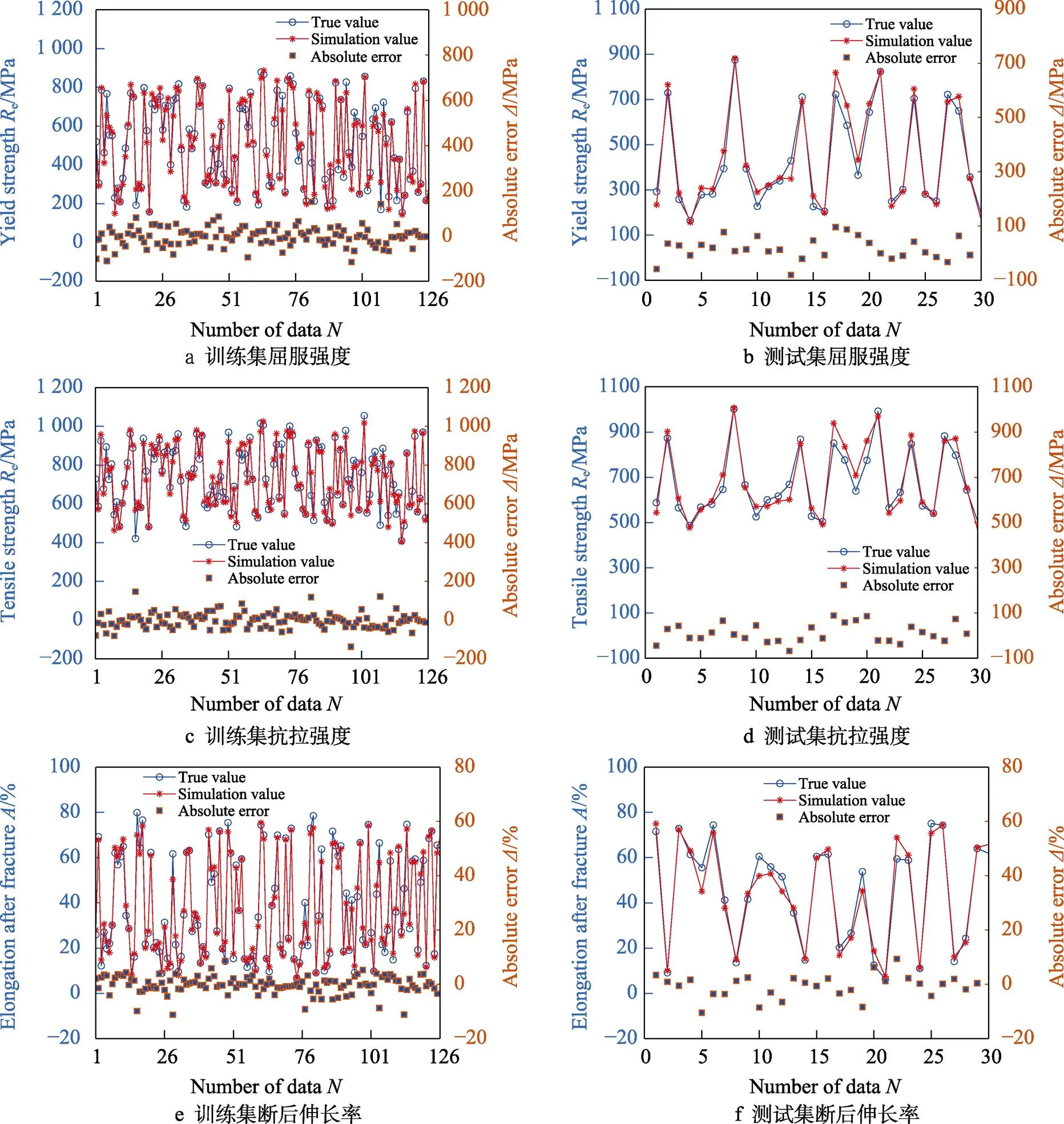
图6 真实值与仿真值比较
表6 测试集的部分数据及相对误差
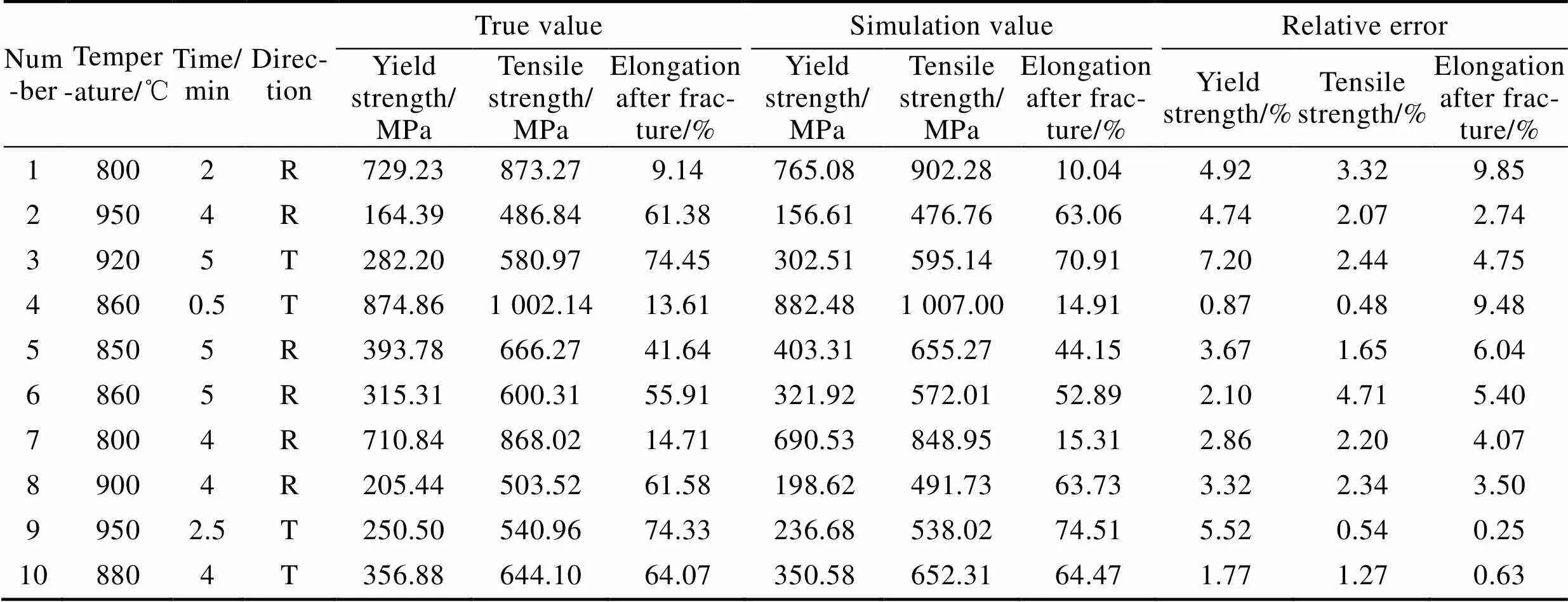
Tab.6 Partial data and relative error of testing set
表7 训练集和测试集的平均相对误差

Tab.7 Average relative error between training set and testing set
表8 BP算法性能比较

Tab.8 Performance comparison of BP algorithms
表9 各种算法性能比较

Tab.9 Performance comparison of different algorithms
5 MEA-BP模型的应用验证
5.1 热处理质量综合量化评价方法
借鉴环境影响定量评价的方法[25-26],曹双安等[27]将多个指标的综合量化应用于热处理质量的评价。相关定义如下:
等价性能指数:
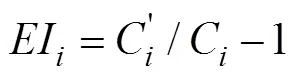
综合性能指数:

国家标准规定的退火态316L不锈钢力学性能要求[28]见表10。为使退火态316L具有良好的强度和塑性,在屈服强度满足要求的条件下,权值系数可取为抗拉强度:伸长率=1:1来对热处理质量进行量化评价。
5.2 评价结果
为了考察316L奥氏体不锈钢热处理力学性能MEA-BP神经网络模型的实际应用效果,将模型引入某企业的退火生产线。用MEA-BP神经网络模型对未使用的退火工艺参数进行力学性能预测,采用前述热处理质量综合评价方法对热处理质量进行量化评价。某企业中厚度为0.02~0.05 mm的316L不锈钢退火工艺为:退火温度950 ℃,钢带运行速度10~ 15 m/min,退火炉长10.8 m,退火时间0.72~1.08 min。企业所用退火工艺参数及部分工艺参数的试验值与预测值的热处理量化评价结果见表11。
由表11可见,按照抗拉强度:伸长率=1:1的权值系数对热处理质量进行评价时,退火温度为940 ℃,保温时间为2.5 min或退火温度为960 ℃,保温时间为1.5 min时,316L不锈钢具有较好的综合力学性能。与企业所用的退火工艺(退火温度为950 ℃,保温时间为1 min)相比,不同退火工艺下的综合性能值分别提高了0.75%、19.53%、11.92%、13.98%。预测值与试验值相比,不同退火工艺下的综合性能值相对误差分别‒5.25%、5.02%、11.26%、5.53%。
表10 退火态316L不锈钢力学性能
表11 热处理量化评价结果
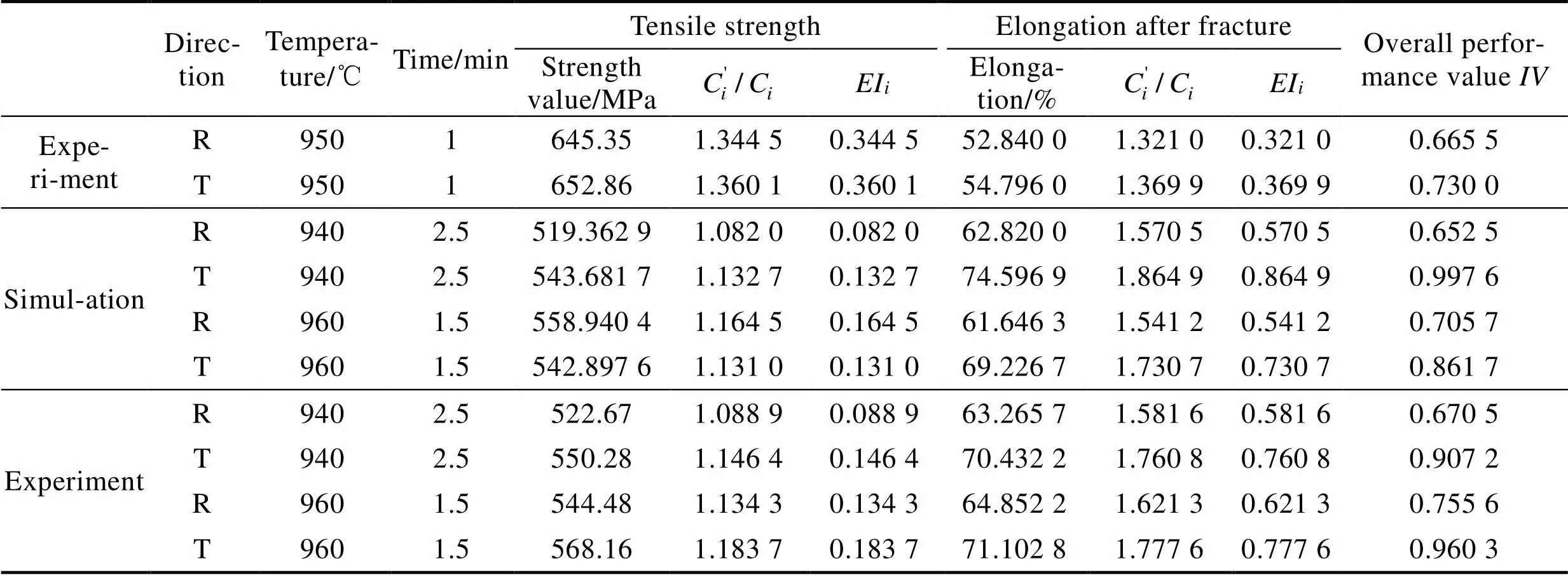
Tab.11 Quantitative evaluation results of heat treatment
Note: the first set of experimental data is obtained according to the parameter experiment of the enterprise described.
总之,316L不锈钢极薄带力学性能预测MEA- BP神经网络模型不仅收敛速度快、稳定性好、预测能力好、预测精度高、泛化性好,而且在退火生产线上具有较好的应用效果,可实现智能控制的要求,节省了大量的人力、物力和财力。
6 结论
1)对316L不锈钢极薄带进行拉伸试验,发现退火温度和保温时间对316L的力学性能有较大影响,轧向R和横向T的力学性能表现出明显的各向异性。
2)采用3×6×14×3四层拓扑结构的MEA-BP神经网络模型在训练集和测试集上都具有较低的误差,拥有较好的预测能力、预测精度和泛化能力。测试集中屈服强度、抗拉强度和断后伸长率的平均相对误差分别为8.92%、5.21%和9.28%;数据集总体相关系数为0.980 94,真实值与仿真预测值之间高度相关,实现了对热处理极薄带力学性能的高精度预测。
3)对不同层数的MEA-BP神经网络模型的研究结果表明,双隐含层神经网络的预测能力和预测精度高于单隐含层。
4)对标准BP和智能算法优化BP神经网络模型的性能进行比较,结果表明,智能算法优化后的BP神经网络模型具有更低的训练误差,但也容易造成过拟合,使得测试集误差升高;MEA-BP神经网络模型具有更好的预测能力和预测精度。
5)采用热处理质量的综合量化评价方法对316L不锈钢极薄带退火后的综合力学性能进行评价,与企业现用生产工艺相比,模型优化后工艺的综合性能值有显著提高。利用神经网络模型能够根据不同生产情况灵活修改生产工艺参数,节约成本。
[1] 任忠凯, 郭雄伟, 范婉婉, 等. 精密极薄带轧制理论研究进展及展望[J]. 机械工程学报, 2020, 56(12): 73-84.
REN Zhong-kai, GUO Xiong-wei, FAN Wan-wan, et al. Research Progress and Prospects of Precision Ultra-Thin Strip Rolling Theory[J]. Journal of Mechanical Engineering, 2020, 56(12): 73-84.
[2] MISHRA M K, DUBEY V, MISHRA P M, et al. MEMS Technology: A Review[J]. Journal of Engineering Research and Reports, 2019: 1-24.
[3] 肖白. 我国冷轧(宽)板带生产现状及发展趋势[J]. 中国冶金, 2004, 14(4): 12-16.
XIAO Bai. Production of Cold Rolled Strip and Development Trend in China[J]. China Metallurgy, 2004, 14(4): 12-16.
[4] 易丹青, 许晓嫦. 金属材料热处理[M]. 北京: 清华大学出版社, 2020: 85-86.
YI Dan-qing, XU Xiao-chang. Heat Treatment of Metallic Materials[M]. Beijing: Tsinghua University Press, 2020: 85-86.
[5] 陈明. MATLAB神经网络原理与实例精解[M]. 北京: 清华大学出版社, 2013: 156-157, 165.
CHEN Ming. Principle of MATLAB Neural Network and Exact Solution of Examples[M]. Beijing: Tsinghua University Press, 2013: 156-157, 165.
[6] HILL T, MARQUEZ L, O'CONNOR M, et al. Artificial Neural Network Models for Forecasting and Decision Making[J]. International Journal of Forecasting, 1994, 10(1): 5-15.
[7] BENARDOS P G, VOSNIAKOS G C. Optimizing Feedforward Artificial Neural Network Architecture[J]. Engineering Applications of Artificial Intelligence, 2007, 20(3): 365-382.
[8] 朱文轩. 人工神经网络在机械工程领域中的应用[J]. 南方农机, 2020, 51(24): 160, 163.
ZHU Wen-xuan. Application of Artificial Neural Network in Mechanical Engineering Field[J]. China Southern Agricultural Machinery, 2020, 51(24): 160, 163.
[9] 李志峰, 麻永林, 冯岩, 等. 神经网络在冷轧301S不锈钢极薄带材表面硬度预测中的应用[J]. 钢铁, 2014, 49(5): 63-67.
LI Zhi-feng, MA Yong-lin, FENG Yan, et al. Applications of Neutral Network in Surface Hardness Prediction for Cold Rolling 301S Stainless Steel Thin Strip[J]. Iron & Steel, 2014, 49(5): 63-67.
[10] 路泽永. 基于BP神经网络算法的耐磨钢热处理工艺优化[J]. 热加工工艺, 2016, 45(22): 168-171.
LU Ze-yong. Heat Treatment Process Optimization of Wear Resistant Steel Based on BP Neural Network Algorithm[J]. Hot Working Technology, 2016, 45(22): 168-171.
[11] 张学宾, 谷继华, 宋克兴, 等. 尺寸效应下Cu-Ag合金强度的神经网络预测[J]. 河南科技大学学报(自然科学版), 2021, 42(2): 1-6, 117.
ZHANG Xue-bin, GU Ji-hua, SONG Ke-xing, et al. Strength Prediction of Cu-Ag Alloys Using Neural Networks Model Based on Dimensional Effects[J]. Journal of Henan University of Science and Technology (Natural Science), 2021, 42(2): 1-6, 117.
[12] 王海涛, 韩恩厚, 柯伟. 用人工神经网络构建碳钢、低合金钢大气腐蚀模型[J]. 腐蚀科学与防护技术, 2006, 18(2): 144-147.
WANG Hai-tao, HAN En-hou, KE Wei. Artificial Neural Network Modeling for Atmospheric Corrosion of Carbon Steel and Low Alloy Steel[J]. Corrosion Science and Protection Technology, 2006, 18(2): 144-147.
[13] DING Shi-fei, SU Chun-yang, YU Jun-zhao. An Optimizing BP Neural Network Algorithm Based on Genetic Algorithm[J]. Artificial Intelligence Review, 2011, 36(2): 153-162.
[14] JIN Wen, LI Zhao jia, WEI Luo-si, et al. The Improvements of BP Neural Network Learning Algorithm[C]// WCC 2000-ICSP 2000.2000 5th International Conference on Signal Processing Proceedings. 16th World Computer Congress. Beijing, China: IEEE, 2002: 1647-1649.
[15] 邱锡鹏. 神经网络与深度学习[M]. 北京: 机械工业出版社, 2020: 90-92.
QIU Xi-peng. Neural Networks and Deep Learning[M]. Beijing: China Machine Press, 2020: 90-92.
[16] 田野. 基于进化算法的复杂多目标优化问题求解[D]. 合肥: 安徽大学, 2018: 20-25.
TIAN Ye. Solving Complex Multi-Objective Optimization Problems by Evolutionary Algorithms[D]. Hefei: Anhui University, 2018: 20-25.
[17] EIBENÁ E, HINTERDING R, MICHALEWICZ Z. Parameter Control in Evolutionary Algorithms[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 124-141.
[18] DASGUPTA D, MICHALEWICZ Z. Evolutionary Algorithms in Engineering Applications[J]. IEEE Transactions on Evolutionary Computation, 1998, 2(2): 72
[19] 刘雪, 田云娜, 田园. 群智能算法研究综述[J]. 信息与电脑(理论版), 2021, 33(24): 63-69.
LIU Xue, TIAN Yun-na, TIAN Yuan. A Survey of Swarm Intelligence Algorithms[J]. China Computer & Communication, 2021, 33(24): 63-69.
[20] 杨洋, 陈家俊. 基于群智能算法优化BP神经网络的应用研究综述[J]. 电脑知识与技术, 2020, 16(35): 7-10, 14.
YANG Yang, CHEN Jia-jun. Review on Application of Intelligent Algorithm to Optimize BP Neural Network[J]. Computer Knowledge and Technology, 2020, 16(35): 7-10, 14.
[21] 周英, 卓金武, 卞月青. 大数据挖掘: 系统方法与实例分析[M]. 北京: 机械工业出版社, 2016: 265-266.
ZHOU Ying, ZHUO Jin-wu, BIAN Yue-qing. Using Big Data to Build Your Business[M]. Beijing: China Machine Press, 2016: 265-266.
[22] 孙承意, 谢克明, 程明琦. 基于思维进化机器学习的框架及新进展[J]. 太原理工大学学报, 1999, 30(5): 453-457.
SUN Cheng-yi, XIE Ke-ming, CHENG Ming-qi. Mind Evolution Based Machine Learning Framework and New Development[J]. Journal of Taiyuan University of Technology, 1999, 30(5): 453-457.
[23] WANG Wen-xu, TANG Rui-chun, LI Cheng, et al. A BP Neural Network Model Optimized by Mind Evolutionary Algorithm for Predicting the Ocean Wave Heights[J]. Ocean Engineering, 2018, 162: 98-107.
[24] 郭红戈, 谢克明. 基于反思的思维进化算法[J]. 太原理工大学学报, 2011, 42(3): 232-234.
GUO Hong-ge, XIE Ke-ming. MEA Design Based on Consideration[J]. Journal of Taiyuan University of Technology, 2011, 42(3): 232-234.
[25] SONNEMANN G W, SCHUHMACHER M, CASTELLS F. Framework for the Environmental Damage Assessment of an Industrial Process Chain[J]. Journal of Hazardous Materials, 2000, 77(1-3): 91-106.
[26] 刘江龙, 陈红兵, 李晖, 等. 常用钢的环境影响定量评价研究[J]. 钢铁, 2002, 37(4): 63-65.
LIU Jiang-long, CHEN Hong-bing, LI Hui, et al. Quantitative Assessments for Impact of Common Steels on Ecological Environment[J]. Iron and Steel, 2002, 37(4): 63-65.
[27] 曹双安, 罗新民, 陈康敏. 热处理质量的综合量化评价方法和应用[J]. 金属热处理, 2004, 29(12): 74-76.
CAO Shuang-an, LUO Xin-min, CHEN Kang-min. Evaluation Method of Comprehensive Quantization on Heat Treatment Quality and Its Application[J]. Heat Treatment of Metals, 2004, 29(12): 74-76.
[28] 不锈钢棒: GB/T 1220—2007[S]. 北京: 中国标准出版社, 2007.
Stainless Steel Bar: GB/T 1220‒2007[S]. Beijing: Standards Press of China, 2007.
Prediction of Mechanical Properties of Heat-treated 316L Ultra-thin Strip Based on BP Algorithm
ZHANG Zhi-xiong1a,1b, FU Yong-wei1a, WANG Tao1a,1b, WANG Bin1b, XIONG Xiao-yan1a, WANG Tian-xiang2
(1. a. College of Mechanical and Delivery Engineering, b. Engineering Research Center of Advanced Metal Composites Forming Technology and Equipment, Ministry of Education, Taiyuan University of Technology, Taiyuan 030024, China; 2. Shanxi Taigang Stainless Steel Precision Strip Co., Ltd., Taiyuan 030006, China)
The work aims to predict the mechanical properties of heat-treated stainless steel ultra-thin strip, optimize the heat treatment process, and achieve intelligent control of heat treatment, and constructs a neural network model based on BP algorithm. The heat treatment experiment and tensile experiment were carried out on 316L stainless steel ultra-thin strip. The annealing temperature, holding time and sampling direction of the heat treatment of 316L stainless steel ultra-thin strip were taken as the input layer parameters. The yield strength, tensile strength and elongation after fracture were taken as the output layer parameters. BP algorithm was used to construct the BP neural network model optimized by the mind evolutionary algorithm for predicting the mechanical properties of 316L stainless steel ultra-thin strip and the prediction and application verification of the model were carried out.The effects of different hidden layer nodes and different BP neural network models on performance were considered. The average relative errors of yield strength, tensile strength and elongation of BP neural network model testing set optimized by mind evolutionary algorithm were 8.92%, 5.21% and 9.28%. In addition, the correlation coefficient of training set was 0.980 94. The minimum error sum of single and double hidden layers of BP network optimized by mind evolutionary algorithm was 0.578 6 and 0.546 9 respectively, and the minimum sum of BP network and BP network optimized by mind evolutionary algorithm was 0.579 9 and 0.546 9 respectively. The BP neural network model optimized by mind evolutionary algorithm has a good prediction ability, high prediction accuracy and good generalization ability. Compared with the current production process of enterprises, the comprehensive properties of the production process after model optimization is significantly improved.
BP neural network; mind evolutionary algorithm; 316L; ultra-thin strip; heat treatment; integrated quantification
10.3969/j.issn.1674-6457.2023.02.009
TG156
A
1674-6457(2023)02-0068-10
2022‒08‒23
2022-08-23
国家自然科学基金(51974196,51901151);山西省科技重大专项(20181102015);中国博士后科学基金(2020M680918,2021T140503)
National Natural Science Foundation of China (51974196, 51901151); Shanxi Science and Technology Major Project (20181102015); China Postdoctoral Science Foundation (2020M680918, 2021T140503)
张志雄(1989—),男,博士,副教授,主要研究方向为金属材料塑性成形及其强韧化。
ZHANG Zhi-xiong (1989-), Male, Doctor, Associate professor, Research focus: plastic forming and strengthening, and toughening of metal materials.
王天翔(1965—),男,正高级工程师,主要研究方向为不锈钢精密带钢轧制工艺与装备。
WANG Tian-xiang (1965-), Male, Senior engineer, Research focus:stainless steel precision strip rolling process and equipment.
张志雄, 付永伟, 王涛, 等. 基于BP神经网络算法的316L不锈钢极薄带热处理力学性能预测[J]. 精密成形工程, 2023, 15(2): 68-77.
ZHANG Zhi-xiong, FU Yong-wei, WANG Tao, et al. Prediction of Mechanical Properties of Heat-treated 316L Ultra-thin Strip Based on BP Algorithm[J]. Journal of Netshape Forming Engineering, 2023, 15(2): 68-77.
