双能X射线图像融合技术研究

樊 港，尤瀚庭，罗程远

（东华理工大学机械与电子工程学院，南昌 330013）

0 引言

在工业X射线检测领域，复杂结构或由多种材质构成的样品存在区域厚度和密度多样性。单能射线透射成像是无法顾及到每个区域的成像效果，使用低能射线成像时，X射线可能无法完全透过厚度较大区域，导致厚度较大区域无法成像；反之使用高能射线成像时，X射线透过厚度较小的区域时射线衰减率极小，会导致厚度较小区域图像信息的丢失。双能射线成像系统解决了此类问题，当高能X射线穿透物体时，能量的吸收主要取决于材料的密度，高能扫描主要获取厚度较大区域的图像信息。当低能量的X射线透射物体时，能量的吸收主要取决于材料的有效原子序数以及物体的厚度，低能扫描主要获取厚度较低区域的图像信息。将采集到的高低能图像进行配准融合，可使得X射线图像能呈现物体完整的内部信息。

随着图像融合技术的发展，很多算法取得不错的进展。但不同的算法在融合效果上存在不同层面上的问题。算术平均融合后的图像清晰度比小波变换后的图像低，而小波变换融合后的图像会有背景噪声和重影效应。其余的算法也一定程度上无法完全融合高能和低能图像的细节与纹理信息。为此，本文采用了一种配准融合、去噪增强双能量X射线图像的组合方案，使所得图像更适合于工作人员的后期观察和解读。

1 基于SIFT算法的图像配准

实验中采用的是单源单探结构的真双能检测系统，系统结构如图1所示。该系统的特点是使用一个X射线源和一组探测器，扫描被检物体两次。在第一次扫描时，X射线源被置到低能级，获得低能图像。在第二次扫描时，X射线源被置到高能级，物体再次被扫描，获得高能图像。由于样品架台存在一定的机械误差和采集延迟误差，采集的图像存在一定空间位置上的偏移，直接融合会使高低能图像的信息不能完全吻合，将会使得图像信息更加难以分辨。对此，实验首先采用SIFT算法对高低能图像进行配准。

图1 双能成像系统结构

SIFT算法在图像特征尺度选择的思想上建立图像的多尺度空间，在不同尺度下检测到同一个特征点，确定特征点位置和其所在尺度，达到尺度抗缩放的效果。对一些对比度较低的点以及边缘响应点进行剔除，并提取旋转不变特征描述符以达到抗仿射变换的目的[1]。其算法分以下4步：

（1）尺度空间的极值检测：在所有尺度空间中搜索图像，并通过高斯差分函数确定对尺寸和旋转不变的关键点。

（2）特征点定位：在每个候选位置中，使用一个拟合精细的模型来确定位置尺度，关键点的选择依据于它们的稳定性。

（3）特征点方向确定：根据图像局部梯度的方向,一个或多个方向被分配给关键点，基于这个关键点进行一系列后续操作[2]。

（4）特征点描述：在每个特征点附近，在选定的尺度上测量图像的局部梯度。这些梯度作为关键点的描述符，它允许比较大的局部形状的变形或光照变化[3]。

实验中对日常中的一种自拍杆进行高低能量透射，所采集的两张X射线图分辨率为767×580，如图2所示，高能图像可观察到自拍杆中的一些细节结构，但无法清晰呈现布袋的形状。低能图像清晰呈现布袋的形状却忽略了自拍杆的细节。

图2 待配准融合的高低能X射线图和自拍杆

对采集的两张图像进行SIFT特征匹配，该组图像最终提取了7对特征点进行配对，其结果如图3所示。特征点匹配图建立了高能和低能图像之间的对应关系，有利于后期的融合[4]。

图3 特征点匹配

2 基于小波的图像融合

基于小波的图像融合的一般程序可以描述如下：

（1）使用离散小波变换（DWT）将源图像分别转化为相应的小波系数图像；

根据上述分析，产业创新速度对创新效益的影响可能存在非线性关系，即门槛效应。以单门槛为例，如果存在1个创新速度门槛水平τ，当S≤τ以及S＞τ时，产业创新速度对创新效益的弹性系数并不一致，并呈现出显著的差异，为此引入虚拟变量Di:

（2）按照融合规则，由源图像对应的小波系数计算得到融合后的小波系数[5]；

（3）将离散小波逆变换（IDWT）应用于融合后的小波系数，用来重建融合后的图像。

融合规则在基于小波的图像融合中起着至关重要的作用。小波变换有两类普遍的融合规则：基于像素的规则和基于区域的规则。对于基于像素的融合规则，融合后的小波系数的值由源图像的相应小波系数决定。对于基于区域的融合规则，融合后的小波系数由源图像的相应小波系数以及它们周围的小波系数来定义。

本文选择采用基于像素的融合算法。该方法首先对两个源图像的近似系数分别应用低通滤波器，生成融合图像的近似系数。接下来，将两个源图像的相应细节系数相加，得到融合图像的细节系数。最后，将得到的近似系数和细节系数用来重建融合图像。

假设L表示实验场景中的低能量X射线图像，H表示相应的高能量X射线图像，F表示所产生的融合图像[6]。实现基于小波的图像融合的过程如下。

（1）分别获得L和H的小波分解。为了对L和H进行DWT，需要选择能够代表图像细节的小波族和小波基。实验中选择使用一个能够代表足够细节变化的小波基，而不考虑小波族。分解所需的尺度大小是另一个需要确定的问题，太少的尺度会导致融合后的图像损失太多的细节，而太多的尺度会导致融合后的图像变得粗糙。在双能量X射线图像上进行了多次实验，结果表明，选择4个尺度一般会产生良好的效果。

（2）对L和H的近似系数分别应用一个低通滤波器，以产生融合图像的近似系数。然后，对L和H的近似系数进行平均化处理，得到融合图像的近似系数F，如式（1）所示：

其中，WφF、WφL和WφH分别是F、L和H的近似系数。

（4）对在步骤2和3中分别获得的近似系数和细节系数进行IDWT，构建融合图像F，图像F如图4所示。基于小波的融合结果显示了更多自拍杆的细节和布袋的形状，并且具有更好地对比度。然而，该图像有明显的重影和噪声。

图4 小波融合图像

3 消除背景噪声和图像增强

实验得到的双能图像有嘈杂的背景，尽管融合后的图像通常能显示出更多的细节信息，但背景噪声仍然存在，甚至被放大，使图像的进一步处理和解读变得困难。因此，为了使处理后的图像有良好的增强和降噪效果，本文设计组合基于背景减法的去噪方法和基于灰度级分组的增强方法。

3.1 基于背景减法的去噪

在融合后的图像中选择噪声背景的一个样本斑块，得到其直方图H B(k)。背景补丁是图像的一个角。噪声背景补丁的直方图是由图4所示的小波融合图像的直方图进行重新缩放和减去所得，如式（3）所述：

其中，k=0,1,…,M-1。H0(k)是原始图像的直方图，N0是原始图像中的像素数，N B是噪声背景样本斑块中的像素。β是一个系数，可以适当调整H B(k)的振幅，实验中假设其值为0.87。由此得到修改后的直方图H(k)，减去噪声的图像如图5所示。降噪后的图像效果良好，伪影和噪声基本被消除。

图5 降噪后的图像

3.2 基于灰度级分组的图像增强和重建

实验中使用一种称为灰度级分组（GLG）的图像增强技术，在灰度直方图上进行算法上的操作。在对比度较低的图像中，其直方图灰度大多集中在某一区域，整个算法的目的就是让灰度级更合理地分布在直方图上[7]。振幅小的灰度级应当距离相对较近，反之，振幅大的灰度级则应当相距较远。

对于降噪后的图像，首先得到它的统计直方图H(k)。再将强度值非0的所有灰度级作为初始组G(i)，初始化L(i)和R(i)，将它们分别作为每个组灰度级大小的左、右边界。

算法中每一次循环按照如下步骤进行。

（1）找到所有组中最小的强度值，记录其下标，在该组左右两边寻找较小的组与其组成一个新的组，更新G(i)、L(i)、R(i)。

（2）计算灰度级转换表。计算每组之间的间距N，第一步先把两端的灰度级拉伸至该灰度级的端点，第二步按照组间间距N均匀分布的原则，计算出所有灰度级的转换表T(k)[8]。

（3）把转换函数作用到配准融合和降噪后的X射线图像上，得到新的直方图，计算像素间的平均距离D。循环直到组数为2，再寻找最大的像素平均距离D所对应的转换函数T，并将原始X射线图像转换为最终对比度增强了的图像。图6所示为增强后的图像。与增强前的图像对比，该技术在重建无噪声和增强融合X射线图像上取得可观的效果[9-11]。

图6 增强后图像

4 对比实验

为进一步证明该组合方案的实际效果，本文采用不同算法的交叉组合方案进行对比实验。为了避免实验的偶然性，本文通过同一检测系统采集另外两种不同自拍杆的高低能X射线图像，一种比上文用的自拍杆结构细节更复杂，另一种则相较于更简单。对应的高低能X射线图像分辨率都为767×580。实验中有应用到6种不同算法，按照配准融合、降噪和增强的搭配规则设置出4组组合方案。在相同的实验条件下，利用4种组合方案分别对图像进行处理，4种组合技术都在同一操作系统上完成处理，严格确保实验的客观性。为了方便比较实验处理图像后的结果，引入互信息量作为处理结果的客观评价指标。互信息量反应处理后图像中细节信息的保留程度，其值越高表明处理效果越好，反之其值越低表明处理效果越差[12]。利用Python程序完成4组组合方案的互信息量计算，记录实验结果，得到表1。并根据结果绘制出对比图，如图7所示。其中，a组对应图2中的高低能图像组，b组对应从结构细节更复杂的自拍杆上采集到的高低能图像，c组对应从结构细节更简单的自拍杆上采集到的高低能图像。A~D四种组合方案分别为：A组合为SIFT、小波融合、背景减法、GLG；B组合为SIFT、算术平均法、背景减法、GLG；C组合为SIFT、小波融合、背景减法、直方图均衡化；D组合为SIFT、算术平均法、背景减法、直方图均衡化。

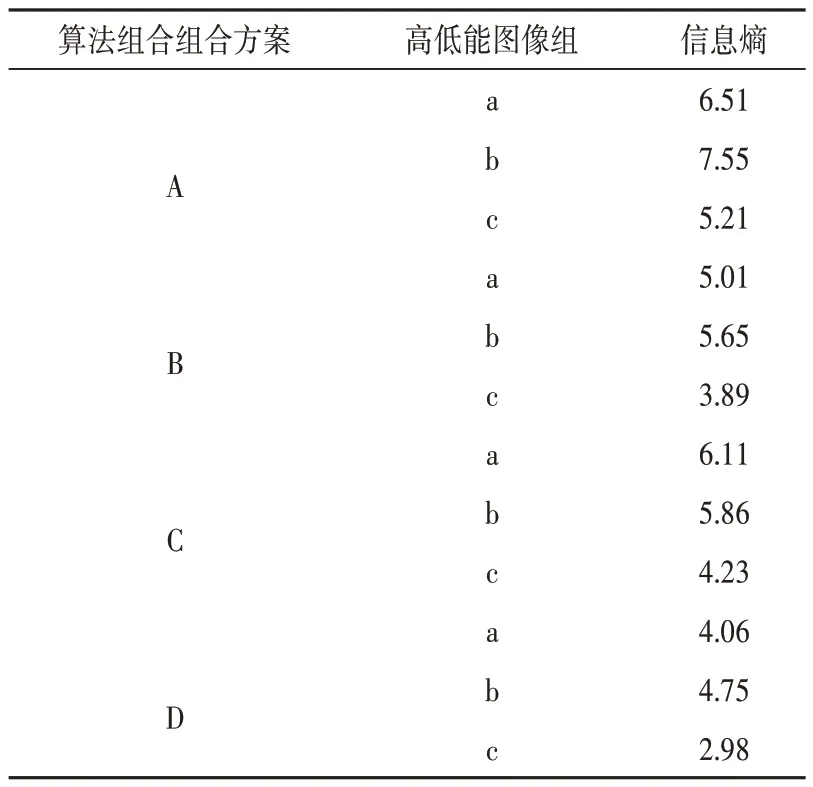
表1 图像的互信息量

图7 4种组合方案实验结果对比

由图7的柱状图可看出，本文的组合算法对细节复杂度不同的高低能图像组处理所得的信息熵都明显高于其他的算法组合，所以该组合算法的处理效果最好。同时，对比处理后的图像发现，本文的组合算法所得的图像未出现失真的现象，其他3种组合算法所得的图像出现不同程度上的失真。因此，通过对比实验可进一步证明，本文提出的组合方案在实际应用中具有最佳的处理效果，能够得到清晰、细节度高的图像。

5 结束语

本文主要对高低能图像的配准融合进行研究，采取了基于SIFT的配准算法、基于像素的小波融合算法、基于背景减法的去噪算法和基于直方图均衡化的增强算法的组合方案。同步设计对比实验，证明了该组合方案在图像配准融合中取得最佳效果，最终的图像不仅包含来自两个源图像的互补信息，并且消除了背景噪声和增强了对比度。