移动机器人的路径规划技术研究*

李晨辉，王泽峰，胡德燕，胡连信，孙凯悦，崔 琳，吴 晟※

（1.哈尔滨工程大学烟台研究（生）院，山东烟台 264000；2.湖州师范学院信息工程学院，浙江湖州 313000；3.烟台市海洋经济研究院，山东烟台 264000；4.天津威图测控技术有限公司，天津 300392）

0 引言

近年来，移动机器人技术得到了进一步发展，是国家科学技术和工业自动化的重要指标之一。机器人技术在提高社会生产力的过程中所占的比重也越来越大。移动机器人在工业场景和家用场景中都有着庞大的需求，具有广阔的前景。如家庭场景下的娱乐机器人、康复机器人、服务机器人、安全保护防护机器人；在工业场景下的快递分拣车AGV（Automated Guided Vehicle）、化学危害气体中的有害气体检测机器人、在路况复杂下的人员搜救机器人。

对于移动机器人，准确的导航对机器人至关重要，而路径规划是决定导航是否精确的重要一环。路径规划是在已知的应用场景中根据初始起点和目标点规划出一条路径。该路径能够满足高效、安全等要求，并且能够及时避开路径上的各种障碍物。移动机器人的路径规划技术主要包括全局路径规划和局部路径规划，其核心内容是实现规划路线的平滑性和冗余性，在外部环境中能够正确地行进。路径规划主要分两步进行：第一步是根据静态障碍物区域和自由可移动区域进行全局路径规划，找出最优路径；第二步是移动机器人在目标点行进中，动态感知周围的局部环境，及时通过局部规划对障碍物进行避障。本文阐述了从全局路径规划到局部路径规划的常用算法的应用机制，在现实场景下的应用情况，并对其算法进行了优缺点分析，对部分研究路径规划的国内外文献进行了概述，并对其进行了分析和讨论。

1 全局路径规划算法对比分析

全局路径规划是依照当前的静态地图，参考地图上障碍物的位置和可行路径，根据系统给出的出发点和目标点，规划出一条最优路径。其相关算法主要应用于场景预知的室外环境中，面对复杂多变的地理环境，通过对算法的优化来提高机器人路径规划的能力。主要包括A*算法、遗传算法、蚁群算法、粒子群算法和快速探索随机树等。

1.1 A＊算法

1968年Nils Nilsson[1]提出了A＊算法，其主要用于在静态环境中求解最短路径，因为其属于遍历的确定性搜索方式，搜索过程直观简洁，所以是解决地图环境预知的情况下全局路径搜索问题的典型算法。在全局网络中，A＊算法会依据扩展节点选择当前“代价”最低的方块进行下一步搜索，直到搜索到终点，从而规划出成本最低的路径。A＊算法是当前流行的比较重要的启发式搜索算法之一，该算法广泛应用于单机器人的全局静态环境中。

A＊算法示意图如图1所示，其中f()n是关于目的地n的估价函数，g()n是“当前代价”，即起点到目的地n的最短路径值；h()n是“预估代价”，即当前移动机器人位置到目的地n的最优路经的启发值。张新艳等[2]引入了基于时间因子的改进型算法来寻找转弯次数较少的路径方案。

图1 A＊算法示意图

1.2 遗传算法

遗传算法（Genetic Algorithm，GA）是美国的Bre⁃mermann[3]于1960年提出，通过选择和交叉变异手段，模拟达尔文的物竟天择、适者生存的法则。在初始化阶段根据表现的外部性状，对种群进行编码，根据适用度函数评估每条路径的适用度，参考适应度越高，选择的概率越大，选择出适应度高的路径，低于适应度选择阈值的进行淘汰处理，在已选出的路径个体中再进行交叉、变异，直至产生达到要求的路径。遗传算法示意图如图2所示。

图2 遗传算法示意图

基于提高遗传算法的全局性，减少陷入局部最优的概率，John Hollnd探索出增加变异算子和交叉算子方法，通过模拟自然状态下的遗传模式并加入了选择算子[4]。对于该算法易于过早的收敛而导致迭代效果不佳，Ge等[5]决定改进原本算法：首先是通过增加了新的预测机制，不在是随机对染色体编码，另外也通过对适应度函数进行改进，提高其评价广度。2018年，A Z Zambom等[6]通过优化遗传算法的执行策略，可在复杂环境中搜索机器人的最优路径。Qu等[7]设计了一种修改算子的方法，能够较好地解决局部最优问题，改善了遗传算法的收敛性差，种群间交叉变异少的问题。

1.3 蚁群算法

蚁 群 算 法（Ant Colony Optimization，ACO）是Dorigol[8]基于正反馈机制提出的一种路径规划算法，结合真实环境下蚂蚁的行为，模拟蚂蚁根据信息素浓度的高低进行路径决策。根据这一特性，在觅食行为中，总能求得一条从出发点到目标点的最优路径。图3显示了这样一个觅食的过程。如图所示，存在一定数量的蚂蚁，设定N点为蚂蚁的巢穴，F为蚂蚁要寻找的食物。蚁群会沿着蚁穴和食物之间的直线距离移动，假设在蚁穴和食物之间出现了障碍物，这时蚂蚁就要做出决策，是向左还是向右行进，由于前面的蚂蚁没有留下信息素，蚂蚁在两个方向的概率是相同的。只有在有蚂蚁停留的地方，就会在相应的地段分泌一定的信息素，而且信息素会随时间的流逝浓度逐渐变低，该物质是蚁群进行信息交流的载体。后面的蚂蚁通过信息素的浓度来做出相应的决策，很明显，沿着较短距离的路径，信息素会越来越浓，进而吸引更多的蚂蚁。

图3 蚁群算法示意图

为了解决蚁群算法容易陷入局部最优点的问题，不少研究者对算法的信息素浓度进行改进。面对蚁群算法搜索速度慢和局部最优，Liu等[9]在该算法基础上加入信息素挥发机制和自适应搜索步长，大大减少了蚁群算法的迭代次数。基于此，Dai等[10]认为改进每次迭代的方法是有效的，通过改进迭代的步长实验表明，与传统的蚁群算法相比，使得改进的ACO迭代次数减少了2/3，快速高效地对路径进行规划证明改进的算法更有效。除此之外，对于多物流机器人的路径规划，杨洋等[11]认为蚁群算法结合弹性时间窗技术，能够实现多物流机器人的路径规划相，经仿真实验表明：快速规划的同时能够实现最优的避障路径。王雷等[12]针对蚁群算法容易陷入局部优化的问题，提出了通过实时调整信息素启发因子和预期启发因子，自适应地改变挥发因子。针对蚁群算法初始信息素不足和收敛速度慢和的问题。张玮等[13]通过加入烟花蚁群混合算法来求解静态环境下的避障问题。

1.4 粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）是由Kennedy和Eberhart[14]在1995年提出。粒子群算法通过不断搜索当前的最优值，通过迭代不断更新粒子的速度和位置，类似于鸟类觅食的过程。通过个体与群体成员的适当交流，整个鸟群都能达到最终的食物源。该算法是通过模拟鸟群，单个鸟与鸟群之间的信息共享，通过计算分析优化，求出最优解。其基本原理是个体与群体协作和信息共享，从而获得最优解。它是一个以当前搜索到的最优值不断更新迭代来寻找全局最优值的算法。粒子群算法是概率型的全局路径规划算法，因为在迭代的过程中充满更多的可能性。PSO通过让单个粒子在路径规划空间里找出此粒子的最优解，再将个体最优解共享给粒子群的其他粒子，找出个体中最优解作为全局最优解，因此整个粒子群在搜索的过程中覆盖的范围更大，更容易找到全局最优解[15]，其算法流程如图4所示。

图4 粒子群算法示意图

针对粒子群算法生成因需要达到全局最优而造成的路径折线较多的和k-means算法易受初始中心影响等问题。Song[16]提出通过加入自适应阶段速度，来减缓机器人路径的折线，优化路径平滑度，同时也提高了搜索空间的能力。汤深伟等[17]提出了基于改进粒子群算法的k-means聚类算法，孟庆宽等[18]通过粒子群算法计算得到最优加权因子，进而调整控制规则实现导航车辆的自适应控制。

针对于标准PSO算法在一些基准函数上改进，PSO算法能快速收敛但是容易陷入局部最优的问题。王东风等[19]基于粒子间适应值的差异，提出对粒子位置高斯采样均值的自适应调整策略，减缓粒子在中心的聚集趋势。Ma等[20]提出将双重仓库下机器人最短路径问题转变为时变非线性规划问题来降低难度。Ajeil等[21]针对静态环境下寻优的问题，通过与GA算法、PSO算法比较，提出通过设置蚁群不同的个体的寿命的优化算法，实验结果表明，在路径规划长度的减少有显著的效果。

1.5 快速扩展随机树

快速扩展随机树（Rapidly-exploring Random Trees，RRT）是通过随机构建空间树来实现快速搜索的一种算法。基本思想是在已知地图上，通过给定的起始位置和目标位置的规划任务，在起始位置通过抽样随机构建随机无向图，类似于树形结构，在无障碍区域不断延伸树形结构。一般来讲，路径规划算法都是不断的朝着目标位置延伸，但是由于障碍物的存在，如果不断的指向目标位置，会有和障碍物相撞的风险。为解决上述问题，RRT算法主要通过随机采样的方法，选择延伸方向时，会设置一定的概率朝着目标位置生长，也有一定的概率随机在全局地图任意方向延伸。扩展树延伸分支选择距离采样点位置近的树节点，并且建立延伸的树节点是否撞到障碍物；采样点距离扩展树的距离要达到设定的阈值，通过两个约束防止发生碰撞和延伸的树节点重复。

对于RRT算法对前期的的扩展比较敏感，全局最优解由于扩展树的结构，导致收敛速度慢的问题。基于此，N Pérez Higueras等[22]通过将强化学习的思想运用到RRT算法上，提出了一种改进型算法，改进初期的代价函数，使其在前期能够快速的找到较优扩展方向，从而加快收敛速度。符秀辉等[23]通过加入对扩展方向的自适应策略，减少了RRT算法达到最优路径的迭代次数，并且对RRT算法前期存在的偏差较大的问题有了一定的改善。由于RRT算法在障碍物较多，且空间比较复杂的环境中，容易陷入局部最优值，甚至是找不到最优解，朱冰等[24]通过提出增加约束来调整扩展的方向，分别设定了安全场约束和对于扩展树的角度进行了限制，增强了RRT系统的鲁棒性。Wang等[25]提通过卷积搭建神经网络，训练预测模型，提前预测扩展树的生长方向，提出通过卷积神经网络与RRT相结合的改进型算法，通过提前将大量成功寻找最优路径数据作为训练集，喂入模型，每次给出最优的多个预测的生长方，再通过RRT进行抽样，大大减少了随机性较大，偏差性大的问题，提高了整体的搜索效率。

2 局部路径规划算法对比分析

局部路径规划是移动机器人执行路径规划时的重要一环，对机器人自身的传感器设备依赖性非常高。局部路径规划目前主要应用于动态环境的避障，是移动机器人工作的关键技术之一。局部路径规划技术主要包括动态窗口法以及人工势场算法。

2.1 人工势场算法

人工势场算法由Khatib[26]在1986年提出。该算法是基于物理学上的正负电荷机制，假设起始位置为正电荷，目标位置设置为负电荷，障碍物则设置为正电荷。根据正负相吸引，正正相排斥原则，从而达到机器人与目标点相吸引，与障碍物相排斥的作用。最后通过模拟由正负电荷所激发的电场，根据机器人电场中所受到的合力来改变移动方向，直至到达目标位置。

由于动态障碍物的存在，而全局规划算法只能在地图上规划，无法考虑动态障碍物，一般的局部实时避障容易偏差较大。针对传统人工势场法算法无法达到目标和局部优化的缺点，无人机运动避障人工势场算法本身存在的极小值问题和局部最小值等问题。段建民等[27]为解决路径规划时的最优解问题，提出了将遗传算法与人工势场法相融合方法，通过并行搜索方法，提高了最优解的搜索速度。陈麟杰等[28]采用增加了无人机之间的斥力，同时定义集群的前置形心作为另一个引力源。丁家如等[29]提出了改进人工势场法引力函数。毛晨悦等[30]提出通过生成预规划路径弱化了目标点对无人机的吸引作用，增加了路径的连贯性。

针对传统人工势场法应用于多坐标系机器人避障时无法约束各关节位姿、陷入局部极小后难以逃离的问题，传统人工势场法由于局部极小点问题而导致规划失败。曹博等[31]通过在笛卡尔坐标系内引入引力势场和斥力势场，主动采用线段球体包络盒模型，来测试碰撞模型，提高了系统鲁棒性，降低了陷入局部最优值的风险。沈文君[32]提出了在改进人工势场函数的基础上，通过修改斥力方向的方法来解决传统人工势场法下的典型局部极小点问题。

2.2 动态窗口算法

动态窗口算法（Dynamic Window Approach，DWA）首先要在其速度空间内采取多组的速度，通过计算采样的多组速度数据进行模拟，模拟出在一定时间内的轨迹，通过一种评价函数，对采样的速度的轨迹模拟进行评价打分，选取最优的速度进行执行。DWA算法要先模拟出机器人的运动模型，根据机器人的硬件运行性能对其运动轨迹进行模拟，主要是根据是否为全向移动机器人进行区别。确定好机器人模型后下一步进行速度采样，确定机器人的最小和最大速度的限制，由于机器人的电机力矩有限，存在最大加速度限制，在模拟轨迹是实际达到的速度应该是一个窗口速度。另外，为了保证机器人能够避免撞到障碍物，在最大减速影响下，对其速度进行约束限制。对速度采样完成后，对采样空间内的速度通过评价函数进行评分，记录评价最优的速度样本，进行对机器人驱动。动态窗口算法示意图如图5所示。

图5 动态窗口算法示意图

针对动态窗口法穿越稠密障碍物时存在路径不合理、速度和安全性不能兼顾等问题，王永雄等[33]通过将其速度采样改进，提出将其参数自适应的DWA算法。针对于机器人在一些特定场景下，例如：上下坡路面存在的加速度过大、造成局部的路径偏差过大等问题，张瑜等[34]提出对采样速度空间的运动模型进行改进，对其速度约束进行优化，然后，基于激光里程计对轨迹模拟，对其进行融合，进行误差补偿，改善了特定场景下偏差较大的问题。

基于DWA算法的移动机器人在障碍物环境比较复杂的环境下，难以选择最优路径。基于此常新新等[35]提出一种改进的DWA算法，对移动机器人避障效果进行优化，主要是通过激光雷达探寻到障碍物的方位，根据预先设计的优化方位角范围，选取在范围内的轨迹。改进后的算法在较为复杂的障碍物环境下通过选择较优角度范围，在一定程度上减少了需要评价的轨迹数目，运行效率有所提高。

3 分析和讨论

本文主要对一些常用的路径规划算法进行总结，对一些算法的优缺点和应用场景进行概述，结果如表1所示。

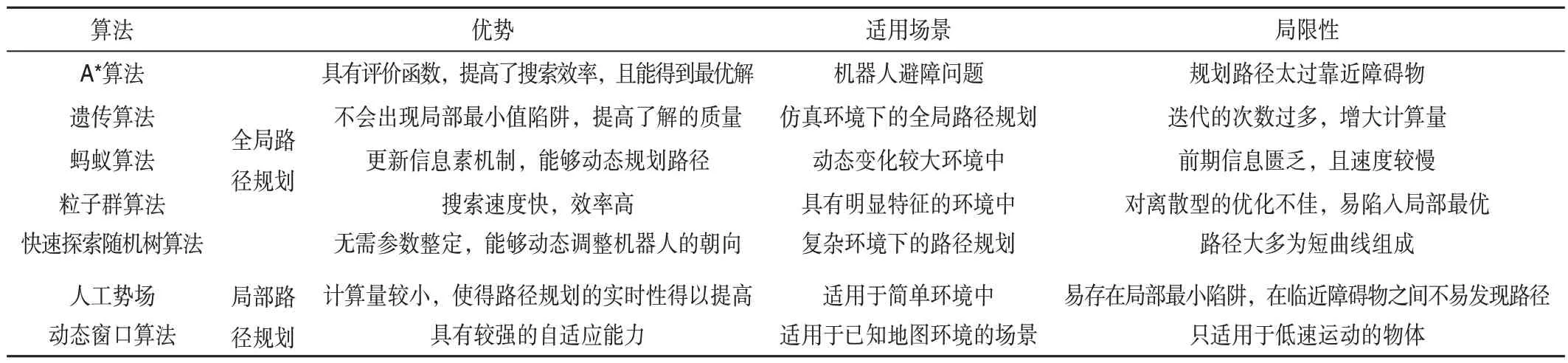
表1 常用路径规划算法表

目前大部分的路径规划算法都已在相应机器人上得以应用。但在现实复杂环境中，一般的算法表现不佳，通过优化已有的常规路径规划算法，已在实际应用中比较广泛，但只能在其特定的理想环境下进行，在实际的场景下，会不可避免地遇到各式各样的问题。根据移动机器人在现实中的需求，将常规的算法在实时性、收敛速度、鲁棒性或者是路径的平滑性等某一方面或某些方面进行相应的改进，同时也要保证路径规划的有效性。针对算法的某一特性进行优化可以快速的提高性能，使其满足现实需求，对算法进行特定方面的进行一般性的改进在实际中应用的较为广泛。目前路径规划算法已经不仅仅局限在单个机器人，已经逐渐应用到集群机器人，以及多机器人多目标的路径规划上，这就提高了规划的难度，在规划最优路径的同时也要将其他机器人算入其中，对实时性、有效性、准确性都有了更高的要求。

由于各种路径规划算法的原理不同，不同算法的应用场景也大不相同，传统的算法具有很强的有效性，但其在实际应用中实用性较差，智能仿生算法一般在收敛速度方面较为迅速，但同时也易于陷入局部最优，单独的算法往往不能成功应用于实际环境中，借助不同算法的优缺点成为解决问题的关键。目前，基于机器学习融合路径规划算法的表现较为优异，基于神经网络，人工智能算法的路径规划算法具有很大的应用潜力。

4 结束语

本文通过研究路径规划算法的原理机制，分析各种算法的优缺点，对部分的改进算法进行了分析，对其应用场景进行了阐述。目前，大部分路径算法已广泛应用移动机器人的路径规划算法中，但当面临现实多变的场景下，移动机器人的路径规划仍然难以满足复杂环境中要求。因此移动机器人在路径效率、路线的优化等问题上需要提高。同时对于不同算法的评价函数，大多都是对障碍物的表示进行不同程度的简化，通常都是近似为矩形、圆形等较为简单的形状，在现实的场景下，可能因过于简化对搜寻最优路径存在影响。