基于神经网络和遗传算法的BK7玻璃精密模压成形多目标优化

罗和喜，李康森，周志文

（深圳大学机电与控制工程学院，广东深圳 518060）

0 引言

光学玻璃模压技术从20世纪80年代开始兴起，是利用高精密模具以及专门模压设备将接近软化的光学玻璃一次性加工成所需要的光学元件，广泛用于摄像机、数码相机、手机、投影仪、CD机、红外探测仪等光电产品中。采用该技术可以直接热压成形精密的非球面光学元件[1]、光学衍射元件[2]、光学微阵列元件[3]、光栅[4]等，给光电行业在光学玻璃加工上带来了新的变化和发展。

玻璃精密模压成形是在高温下产生形变，由于冷却阶段不均匀的温度场等因素，导致最后残余应力仍留在透镜内，从而影响成形透镜的光学性能以及服役寿命。周天丰等[5]建立了改进的模具玻璃界面的摩擦模型，对界面间滑移现象进行分析，并得到微槽阵列的应力分布图。Yi等[6]利用低熔点玻璃K-PG325模压成形了衍射光学元件，用高度6.03 mm直径24 mm的BK7玻璃圆片模压成形出非球面透镜，并对成形过程进行仿真分析，得到残余应力分布以及形貌偏差。Sarhadi等[7]利用玻璃圆环压缩试验验证了Sandwich模型的可靠性，并通过仿真对三维晶片的最终尺寸和残余应力进行评估分析。

冷却阶段，玻璃尺寸收缩、温度不均，热压成形的透镜存在折射率变化和形貌偏差的问题，从而影响玻璃透镜的光学质量。Su等[8]为了修正形貌偏差和折射率变化，提出了一种通过结合仿真结果修改模具尺寸的方法综合补偿透镜的形貌偏差与折射率变化。Puneet等[9]分别对等温模压成形和非等温成形的非球面透镜的形貌偏差进行仿真分析，为了减小偏差值，经过数次迭代计算可以明显地减小形貌偏差。Vu等[10]在非等温模压成形透镜优化中，运用了神经网络与遗传算法对成形工艺进行优化，优化后的玻璃形状偏差有所减小。

基于神经网络和遗传算法寻优计算，寻优结果较为合理，Shen等[11]针对注塑成型工艺特点，为了提高产品的性能质量，利用人工神经网络和遗传算法去优化成型工艺参数，结果表明了基于神经网络技术和遗传算法的注塑成型工艺优化方法是一个有效的工具。Shi[12]和Hsueh-Lin[13]在后续对注塑成型工艺优化分析中，同样采用了人工神经网络和遗传算法，证实了该方法的有效性和可靠性。由于神经网络和遗传算法的优异性质，已被广泛应用到合金成分分析[14]、铝合金压铸[15]、食品冷冻加工[16]、自适应控制和信号处理[17]等领域。

从以上研究成果可以看出，不少学者针对玻璃精密模压成形过程进行了分析，通过有限元软件对成形透镜的残余应力和形貌偏差进行预测，并利用相应的计算方法对透镜质量进行优化分析。而实际生产中，玻璃精密模压成形是复杂的系统，传统工艺参数选择一般通过试错法及个人经验去获取最佳工艺组合，不利于产品开发周期。随着数值模拟技术以及计算机软硬件的日益成熟，利用有限元技术去预测产品的成形质量等技术指标和科学的计算方法去优化工艺方案非常有必要。

本文首先利用正交实验设计方法和有限元技术结合，对BK7透镜模压成形工艺参数进行分析，研究不同工艺参数与成形透镜间的质量规律，选取多个决策变量，以玻璃透镜的最大残余残余应力和最大形貌偏差为优化目标，构建模压成形工艺多目标优化数学模型，利用遗传算法对优化数学模型进行求最优解，从而达到减小透镜的残余应力与形貌偏差。

1 玻璃模压成形多目标优化流程

玻璃模压成形过程中，各个工艺参数对成形透镜的残余应力与形貌偏差的影响呈非线性，且各参数间存在复杂的耦合关系。影响玻璃模压成形的工艺参数主要有模具温度Tm、保温时间ts、模压压力Pm、加压时间tm、保压压力Pk、慢冷时间Ct、快冷时间St、加热时间Th作为控制因子。基于有限元软件建立玻璃精密模压成形的有限元模型，利用正交实验方法指导仿真过程，并实验验证仿真的可靠性。接着将仿真结果作为神经网络预测模型样本数据，构建优化目标（最大残余应力Sm、最大形貌偏差Dm）与决策变量（工艺参数）之间的映射函数关系，用遗传算法对参数进行优化，得到最优工艺参数组合，其多目标优化方法路线如图1所示。

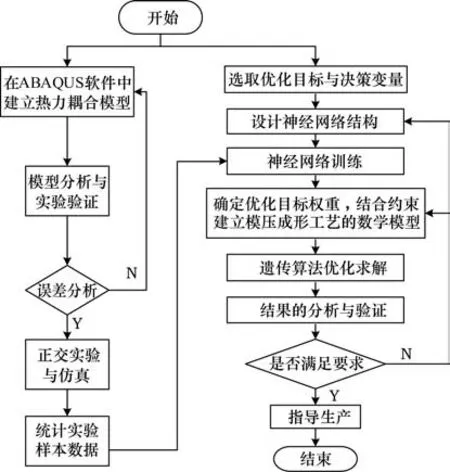
图1 玻璃精密模压成形多目标优化路线

2 有限元模型的建立及仿真

2.1 有限元模型初始化

BK7玻璃材料特性[20]如表1所示，用于热压仿真实验。成形工艺参数取值范围如表2所示，作为优化数学模型的约束条件。

表1 BK7玻璃材料物理属性

表2 BK7玻璃模压成形工艺参数取值范围

仿真模型为二维粘弹性轴对称模型，其边界载荷条件如图2所示，玻璃圆柱的热能大部分来自模具的热传导2 500 W/m2·K，小部分来自氮气对流20 W/m2·K。

图2 边界条件

在热压阶段，分别分析黏弹性模型中应力松弛特性和结构松弛特性存在的差异。玻璃材料的热流变模型采用Arrhenius公式：

式中：ΔH/R为活化能/气体常数之比；Tref为参考温度。

模压过程中剪切应力变化用广义Maxwell模型表示：式中：G(t-τ)为应力松弛函数；G(t)为剪切应力松弛模量函数。

玻璃材料力学特性随温度变化，不同温度下的应力松弛特性用WLF方程表示[21]：

玻璃结构松弛方程如下式所示[22]:

2.2 误差模型建立

如图3所示，模具加热至一定温度保温一定时间，BK7玻璃温度场和应力场如3（a）和3（b）所示，冷却至室温玻璃内部温度场和残余应力如图3（c）和3（d）所示。根据仿真的工艺参数，利用玻璃精密模压设备进行模压实验，热压前后玻璃尺寸变化如图4所示。不难推测出，不同的工艺参数对玻璃的内应力分布以及形貌有很大的影响。

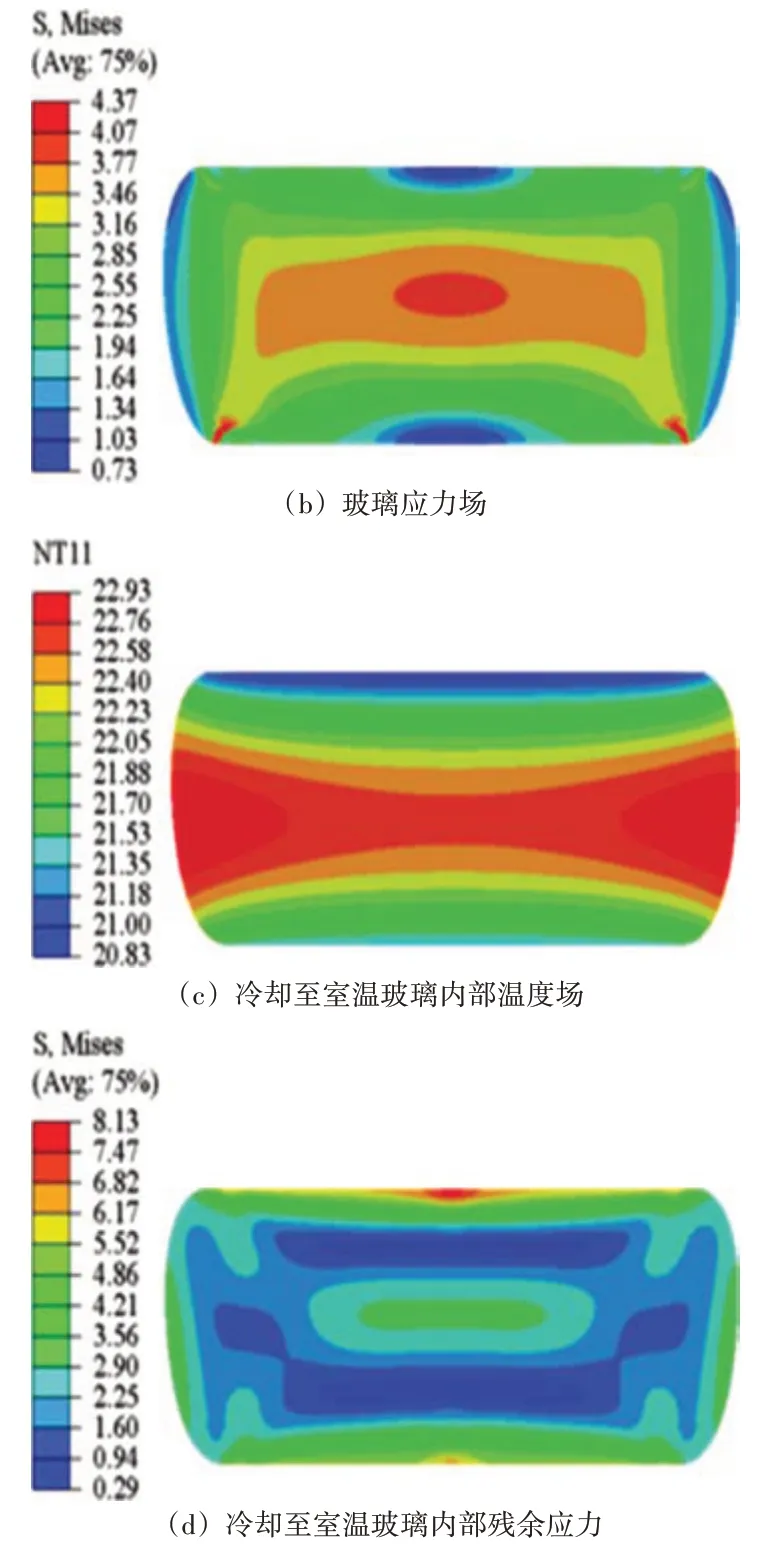
图3 热压玻璃温度场-应力场关系

图4 热压前后玻璃样品的尺寸变化

仿真与实验误差分析如表3所示，误差为δ=(size(f)-size(e))/(s ize(e)-5)，最大变形误差在2.5%，误差在允许范围内。

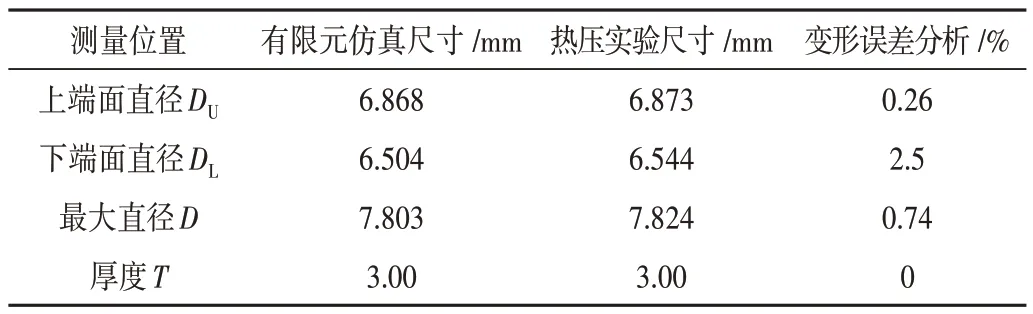
表3 仿真与实验误差分析

2.3 模压参数确定

利用有限元仿真软件ABAQUS对模压过程进行分析，设定合适参数，软件自动精确划分网格进行模拟。热压仿真过程如图5所示，模型为热力耦合模型和热位移耦合模型。

图5 模压仿真过程

双凸玻璃透镜模压成形主要包括：加热、保温、热压、保压退火、快冷脱模这几个阶段。首先把模压腔室里的空气抽空，充入少量氮气防氧化，接着用红外加热装置将玻璃毛坯和模具加热到模压温度，恒温一定时间让玻璃受热均匀，然后施加压力合模，将玻璃模压成形，保持压力一段时间，充入少量氮气慢速冷却至500℃，接着充入大量氮气快速冷却室温，最后脱模取样。

其中，热压温度、模压力、模压速率、冷却速率等工艺参数对成形透镜的残余应力和形貌偏差有着较大的影响。如图6所示，通过获取室温下模具与透镜的坐标信息，然后计算得到透镜的形貌偏差。为了提高实验效率，采用正交实验方法去指导数值模拟分析，如表4所示为BK7玻璃模压成形工艺参数的设置。选取8个因素4个水平的正交表，L32（48），由原来48=65 536次全面实验，现在只需要32次试验。

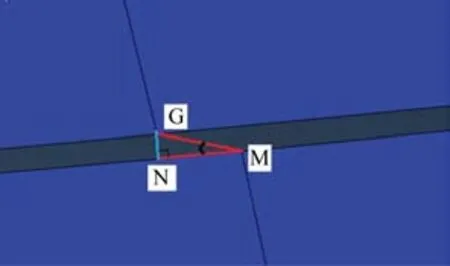
图6 形貌偏差计算

表4 正交实验设计工艺参数及水平设置

3 实验样本数据的处理及正交分析

3.1 实验样本数据的获取

根据实验研究与模拟仿真结果，选定需要优化的工艺参数（Tm,th,ts,Pm,tm,Pk,Ct,St），采用正交实验方法进行实验设计L32-4-9，实验样本结果如表5所示，样本具备均匀分布的特点。

表5 所有正交工艺参数的模拟结果数值

目标函数变量有3个。为了方便求得最优解，需要建立各优化目标间的函数关系。其中，需要优化目标函数有3个，Sm为最大残余应力（MPa）；Sf为成形应力；Dm为最大形貌偏差（µm），各个目标函数线性加权和表示为：

Q为多目标优化问题的评价函数，优化后目标函数为：

3.2 正交实验结果数据分析

首先将正交试验获得的数据进行极差分析，结果如图7所示，本研究最终目的是找出综合评价的Q值的最小值，所以取各因素的4个水平值的平均数（k值）中最小的那一个就是理想的最佳水平值。按照这种逻辑，各因素的理想的最佳水平值就是：A2=650；B4=600；C3=150；D4=10；E3=80；F3=1.5；G4=800；H3=400。而从32组数据中，可以直观搜索到最小的Q值是第6组实验，Q=0.142 28，其对应的各因素的水平值是：A2=650；B2=500；C2=100；D1=4；E1=40；F4=2；G4=800；H3=400。理想最佳和实验最佳相比较，发现只有A2、G4、H3三个因素相同，未达到本研究的预期效果。另外从极差分析中可以看出各因素对最终评价值Q的影响的大小为：A>D>F>B>H>G>C>E。

图7 极差分析

接着对相关数据在SPSS软件中进行方差分析，得出的结果如图8所示，结果显示的各因素的显著性与极差分析是符合的，从具体的数据看，C/E/G三个因素无统计学意义，是可以忽略的因素。其他5个因素的显著性A>D=F>B=H。

图8 方差分析

根据以上两项分析，决定采用神经网络的方法，建立数据量更多，更全面的数据模型，使用遗传算法求出各因素的最佳参数。

4 神经网络模型建立及遗传算法优化

4.1 神经网络模型

在电子科学、计算机科学、控制科学等实际应用中大部分采用BP神经网络[18-19]。图9所示为构建的神经网络模型结构示意图，根据极差分析和方差分析的结果，只采用具有统计学意义的5个因素放入分析模型，即输入层5个神经元，代表的各个工艺参数是：模具温度Tm、加热时间th、模压压力Pm、保压压力Pk、快冷时间St，中间层有两组神经元，每组25个，映射输入层与输出层之间的关系，输出层为优化目标：最大残余应力Sm、成形应力Sf、最大形貌偏差Dm，神经网络结构为8-25-25-3型。

图9 5-25-25-3型神经网络

以模压成形玻璃透镜的残余应力、成形应力和形貌偏差为优化目标，成形工艺参数：模具温度、模压力、保压力、快冷时间、加热时间为决策变量，优化数学模型如下式所示：

决策变量:

最小化：αf n(Sm)+βf n(Dm)+λf n(Sf)

约束条件：

式中：Sm为最大残余应力，MPa；Sf为成形应力；Dm为最大形貌偏差（µm）；f n为归一化函数；α、β为优化目标最大残余应力与最大形貌偏差的优化权重矩阵；Tm、th、Pm、Pk、St为模压成形工艺参数。

4.2 遗传算法优化

遗传算法是模拟生物界中遗传和进化过程的一种自适应寻优算法，直接目标函数作为搜索信息，不依赖梯度信息或其他辅助知识，只需要目标函数和适应度函数，就可以得到较为合理的寻优结果[23-24]。

在遗传算法的求解过程中，交叉概率设为0.7，变异概率为0.1，种群规模为100，进化次数为100。选择技术采用的是轮盘赌原理。个体选择的概率可表示为：

式中：f(x i)为个体x i的适应度；F(x i)为个体的被选择概率；Npop为种群规模。

利用MATLAB中GA遗传算法对构建的多目标优化模型归一化后进行求解，适配度函数如下：

遗传算法经过30次迭代计算见图10，得到最小值为2.3763e-05，其中最优的工艺参数组合为x_best=[649.7，469.9，6.6，0.7，224.1]，即模具温度（Tm）=649.7、加热时间（th）=469.9、模压压力（Pm）=6.6、保压压力（Pk）=0.7、快冷时间（St）=224.1。

图10 遗传算法适应度函数迭代过程

4.3 使用神经网络的遗传算法优化结果讨论与分析

将正交试验获得的数据作为训练样本，为了提高神经网络预测系统的计算可靠性，样本数量为32组。基于表5的样本数据，由于在630℃时，玻璃成形能力较差，需要足够的模压力与模压时间才能完成成形，如表中，成形后玻璃透镜形貌偏差达到35.9 um（未完成形变），所以在进行神经网络训练时，去掉形貌偏差很大的样本数据。图11所示为神经网络训练过程的MSE误差走势，图12所示为神经网络训练、验证、测试回归分析图，训练精度在98.093%，整体精度在百分96.45%，可以较为准确地映射模压成形工艺参数同优化目标最大残余应力、成形应力、最大形貌偏差之间的函数关系。随机挑选几组数据检验网络系统的可靠性，误差分析直方图如图13所示。

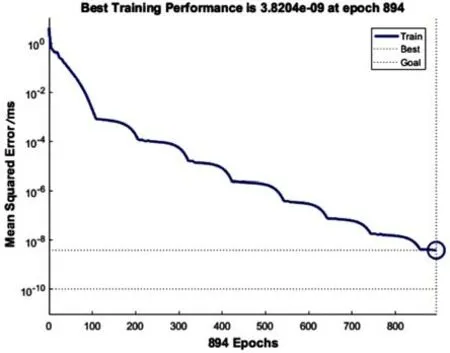
图11 神经网络MSE均方误差分析

图12 神经网络训练回归分析

图13 测试验证误差分析

5 结束语

本文提出基于有限元分析技术、正交试验方法、人工神经网络及遗传算法的BK7玻璃模压成形工艺优化方法，对双凸透镜成形工艺进行了多元优化工艺分析。以模压成形工艺参数：模具温度、保温时间、模压力、加压时间、保压力、慢冷时间、快冷时间、加热时间为决策变量，最大残余应力、成形应力、最大形貌偏差为优化目标，利用实验与仿真结合得到神经网络训练样本，采用人工神经网络系统构建成形工艺参数与优化目标件的函数关系数学模型，并验证神经网络系统的可靠性，接着利用遗传算法进行求最优解，得到可靠的工艺参数，将优化参数再反馈到仿真中，结果表明在神经网络建模的基础上结合遗传算法求最优解对玻璃模压成形工艺的优化是可行的。