结合极坐标建模与神经网络的lVUS 图像分割

刘靖雨，蔡怀宇*，郝文月，左廷涛，贾忠伟，汪毅，陈晓冬

1天津大学精密仪器与光电子工程学院光电信息技术教育部重点实验室，天津 300072；

2 乐普(北京)医疗器械股份有限公司，北京 102200；

3 鲁西南医院，山东 聊城 252325

1 引言

血管内超声(Intravascular ultrasound,IVUS)技术作为一种断层成像技术，可以提供准确描述血管复杂解剖结构的IVUS 图像，被广泛应用于动脉粥样硬化的诊断和介入式治疗[1]。其中，血管主要解剖结构的准确识别是IVUS 图像分析的重要过程之一，可为医生提供可量化的临床参数，作为评价病变程度的重要参考。血管主要解剖结构由内到外依次为管腔区域、内膜边界、斑块区域和中-外膜边界。由于外膜与周围组织的回声差异较小，没有明显边界区分，为便于描述，将中-外膜边界所包围的区域称为血管区域。

IVUS 图像分割算法可用于血管主要解剖结构的自动分割，可分为基于梯度的方法、基于主动轮廓的方法、基于概率的方法和基于深度学习的方法。1995 年，Sonka 等人提出了一种基于图像梯度信息和启发式图形搜索的算法[2]。该算法构建了一个包含图像边缘信息的成本矩阵，并设计了一个合适的成本函数来检测内膜和中-外膜的边界。此类算法的后续研究大多集中在算法自动化[3]和损失函数的设计[4]。基于主动轮廓模型的方法也受到了很多关注。Kovalski等人通过优化内部和外部能量函数，在三维下实现了基于Snake 模型的内膜和中-外膜边界检测[5]。Hernandez等人在应用Snake 模型之前加入受限的各向异性扩散过滤器对IVUS 图像进行滤波处理[6]。Giannoglou 等人则设计了不同的轮廓初始化方法[7]。与此同时，基于统计和概率的方法的效果正在逐渐被认可。研究人员使用各种轮廓建模[8]和区域编码[9-11]来寻找合适的表达血管区域的方式。然而，多数传统分割算法仍面临分割速度慢，易受血管分叉、钙化斑块等结构影响的问题。

近年来，随着卷积神经网络的发展，基于深度学习的IVUS 图像分割算法表现出更加优秀和稳健的性能，成为人们关注的目标。这类算法大多以语义分割模型为基础。Yang 等人提出了第一个 IVUS 图像分割网络，在U 型网络结构的基础上引入了细化分支来获取更丰富的图像特征，并将其命名为 IVUSNet[12]。后来他们又在此基础上进行了网络层数和卷积细节的改进，提出了DPU-Net[13]，并通过设计实时增强控制器来改善训练策略，在分割精度上取得了有效提升。Zhu 等人也从IVUS-Net 中得到启发，以UNet++为基本结构提出了IVUS-U-Net++[14]。Kim 等人则将多尺度输入应用于网络的U 形结构[15]。在文献[16]中，Xia 等人也利用了这种多尺度输入的思想，通过添加深度监控和双向卷积LSTM 模块来优化网络结构。为实现更高精度的IVUS 图像分割，Bajaj 等人将Pix2pix 条件生成对抗网络应用到IVUS 图像分割领域中，针对管腔和血管边缘的不同形态分别设计数据扩增方案并进行训练[17]。Blanco 等人将IVUS 图像进行极坐标变换，利用UNet 网络提供初步分割结果，通过高斯过程回归获得最终的管腔和血管轮廓[18]。最近，根据问题针对性的算法受到关注，Bargsten 等人将胶囊网络架构应用于IVUS 图像分割，以应对小规模数据集的问题[19]。Nishi 等人则针对性地探究了深度学习分割方法在含支架IVUS 图像上的表现[20]。

上述分割网络的研究重点多关注分割精度的提升，也确实取得了良好的效果。但以上算法均将IVUS 图像的分割问题视为对每个像素的分类任务，从像素级层面对分割准确性进行单独评估，而缺少对分割结果整体结构的评价，导致此类算法的部分分割结果无法有效保持其主要血管解剖结构的拓扑结构正确，具体情况包括但不限于：管腔或斑块连通域数量不唯一、斑块连通域未呈现闭合环状、管腔连通域内存在孔洞等。这些错误的拓扑结构不仅不利于管腔直径、斑块厚度等临床参数的准确测量，也不符合医学先验知识，影响医生的后续诊断过程。部分文献通过设计一定的后处理手段来应对这一问题。常用的方法包括ROI区域选择与填充、开闭操作、分割结果轮廓的椭圆拟合等。此类后处理的方式能够显著改善分割结果，但需要根据分割结果的表现具体定制，且计算量大，降低了处理速度。Sinha 等人尝试将后处理步骤集成到网络中[21]，使用基于VGG 的正则化网络直接预测可以代表内膜和中-外膜边界的椭圆参数，再对预测结果进行重建，得到了比较好的结果。但该算法仍然面临以下两个问题：1) 对于一些病变严重的血管，椭圆并不能很好地拟合血管的形状；2) 分开预测代表内膜和中-外膜边界的椭圆参数仍无法保证斑块区域拓扑结构的正确。针对以上问题，在一阶段实例分割模型PolarMask[22]的启发下，本文提出了一种基于极坐标建模和密集距离回归网络的IVUS 图像分割算法，用于提供准确的、符合医学先验知识的血管、管腔和斑块区域分割结果。

2 理论推导

本文算法包括以下几个部分：基于先验知识的极坐标建模、密集距离回归网络，损失函数，以及预测结果重建。

2.1 基于先验知识的极坐标建模

在深度学习分割领域，极坐标建模于2018 年首次应用于显微图像的细胞分割[23]。该方法后在一阶段实例分割方法PolarMask[22]中被证实其泛用性，具有良好的表现。这种建模理念与IVUS 成像中的超声波发射模式具有极高的相似性，原理上适用于描述IVUS 图像中的血管结构，并对整体结构具有约束作用。基于此，结合IVUS 成像原理和血管解剖结构先验知识，本文提出一种适用于IVUS 图像掩膜的极坐标建模方式，以解决IVUS 图像分割结果拓扑关系的保留问题。

2.1.1 先验知识

基于IVUS 成像原理和血管解剖结构的IVUS 图像先验知识总结如下：

1) 数量先验：属于管腔区域和斑块区域的连通域数量唯一。根据IVUS 成像原理，超声探头位于管腔内部，每次扫描仅对一根冠脉的横断面进行完整成像，因此可以理想地认为一张IVUS 图像中具有唯一的管腔区域和唯一的斑块区域。

2) 邻接先验：管腔区域一定不与非血管区域相邻，且一定包含图像中心。这由IVUS 技术成像方式和血管解剖结构所决定。图像中心即为导管中心，因此一定在管腔区域内部。而管腔区域与周围组织则由斑块区域和膜结构隔开。

3) 拓扑先验：斑块区域一定为闭合连续的环状区域，管腔区域一定为闭合的连通域。

2.1.2 极坐标建模

极坐标建模的目的是将先验知识编码成神经网络易于理解的形式。这一建模方式基于一种理想假设：内膜边界或中-外膜边界到图像中心上的任意一点均属于管腔区域或血管区域。符合理想假设的情况如图1(a)所示，不符合理想假设的情况如图1(b)所示。

图1 理想假设示意图。(a) 符合理想假设；(b) 不符合理想假设Fig.1 Ideal hypothesis diagrams.(a) The mask image that meets the ideal hypothesis;(b) The situation that does not meet the ideal hypothesis

这一假设得到了专业医生的认同。仅有极少数存在血管异常压迫或存在心肌桥时的IVUS 图像可能出现不符合理想假设的情况，但由于此类图像没有分割需求，故不在本文算法的考虑范围内。因此，本文所用数据集中的所有标准二维掩膜图像均满足上述三类先验知识及这一理想假设。

建模方式具体描述如下：模拟IVUS 图像采集过程中超声波的发射原理，以图像中心为原点，发射角度间隔均匀的n条射线，射线分别与内膜边界和中-外膜边界相交，得到 2n个交点。在各条射线上，以图像中心到内膜边界交点的距离表示管腔区域，以内膜边界交点到中-外膜边界交点之间的距离表示斑块区域，如图2 所示。通过这种方式，可以将IVUS 图像的二维掩膜图像转换为一维距离向量：

图2 建模示意图。(a) IVUS 原图；(b) 建模结果示意图。内膜边界和中-外膜边界分别用红色和绿色曲线标记，管腔区域和斑块区域建模结果分别使用红色和绿色线段标记Fig.2 Modeling schematics.(a) Original image of IVUS;(b) Schematic diagram of modeling result.The intima contour and media contour are marked with red and green curves,respectively.The modeling results of the lumen area and plaque area are marked with red and green line segments,respectively

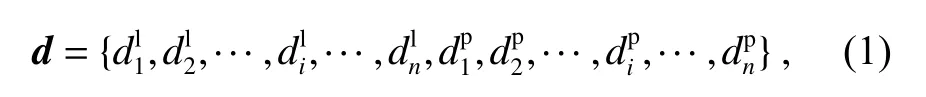
2.2 网络结构

网络结构的设计与建模方式密切相关。根据PCM-PK 特点，建模中心与射线角度和数量固定，网络仅需要对一维距离向量进行预测。因此本文将SEB 模块[24]与残差网络ResNet[25]相结合，构建一种密集距离回归网络，用于一维距离向量的学习与预测，具体网络结构如图3 所示。

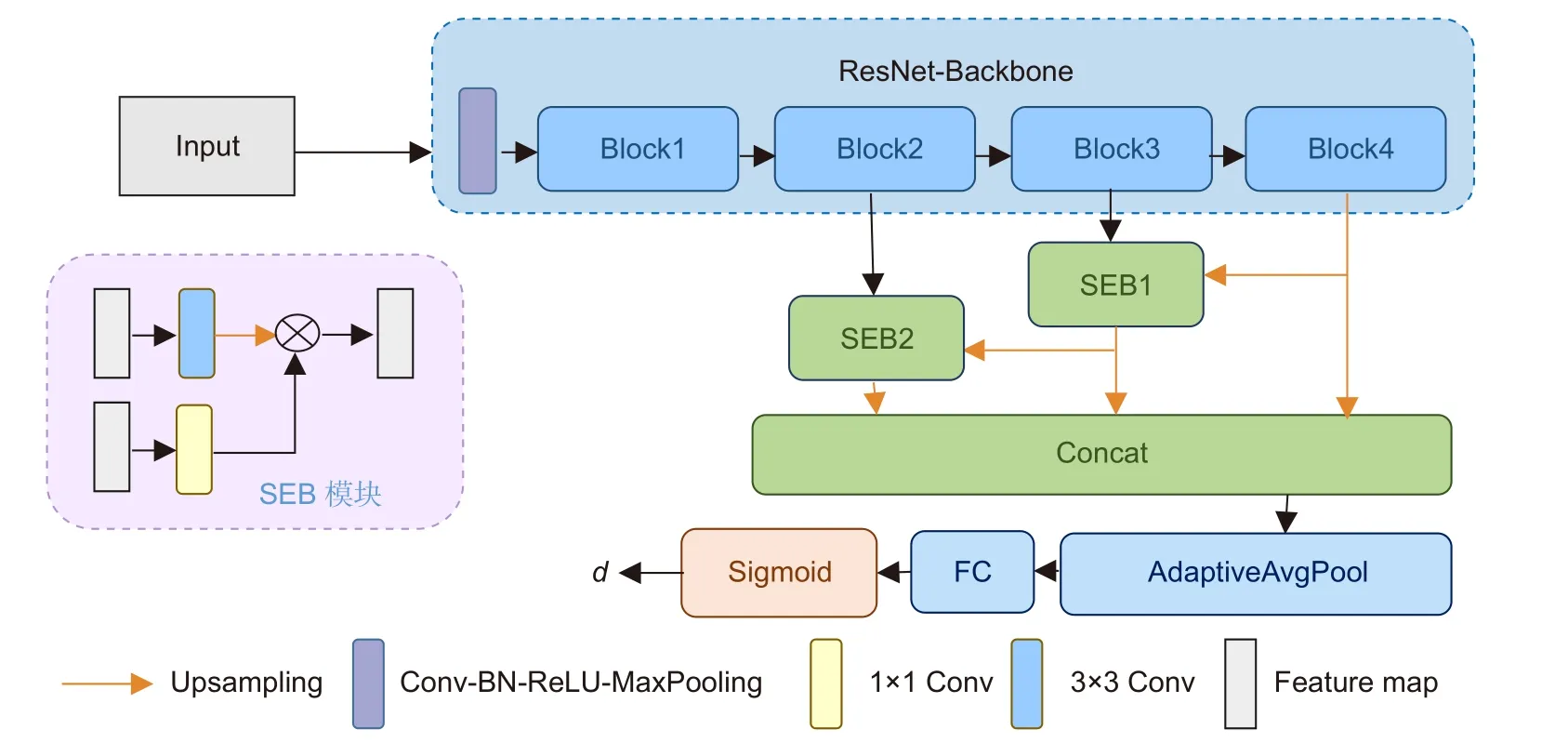
图3 密集距离回归网络结构Fig.3 The proposed dense distance of regression network

该网络选择经过预训练的ResNet 骨架作为骨架网络结构，用于图像特征提取。ResNet 骨架网络不仅通过跃层传播解决了深度网络中梯度消失的问题，还有效减少了参数量，在多项任务中被证明具有优秀的特征提取能力。另外，考虑到一维向量与空间位置息息相关，该网络引入SEB 模块[24]以提高网络对空间信息的关注能力。具体地，SEB 模块能够利用深层特征抑制浅层特征中的背景噪声，并实现二者的有效融合，为网络提供更干净的浅层特征，促使网络关注更多的浅层空间信息。SEB 模块越多，对浅层特征的关注度越高，但相应的运算量和参数量也越大。为了平衡运算速度和对浅层特征的关注程度，算法最终选择在网络中加入2 个SEB 模块。ResNet 结构和SEB模块的结合令网络兼顾了特征提取能力和对空间信息的关注，有利于预测结果准确率的提升。

2.3 损失函数

为有效衡量PCM-PK 建模方式下一维距离向量在网络学习中的损失情况，本文受到离散交并比损失函数(Polar IoU Loss)[22]的启发，构建联合损失函数IVUS Polar IoU Loss。相比于经典的l1,l2和smoothl1等回归损失函数，Polar IoU Loss 考虑了一维距离向量中属于同一对象的元素之间的相关性，能够有效表示一维距离向量管腔区域部分真值与预测结果的实际二维交并关系，因此，使用Ll表示管腔区域的损失函数。n表示建模时预设的射线数量，dl表示一维距离向量管腔区域的真值；表示一维距离向量管腔区域的预测值。

但对于一维距离向量中的斑块区域来说，使用Polar IoU Loss 形式无法准确反映真值与预测值中斑块区域的二维交并关系，某一具体情况如图4 所示,绿色区域表示真值，紫色区域表示预测值。二者相交的部分由红色阴影表示。和分别表示第i条射线上管腔真值距离和预测值距离，和分别表示第i条射线上斑块真值距离和预测值距离。尽管同一射线下真值和预测值内表示斑块区域的距离值接近，但其对应的二维掩膜在该射线方向上实际并未相交。针对这一情况，本文设置代表血管区域真值和预测值的一维距离向量dm,辅助判断。

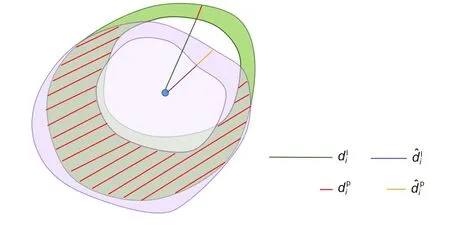
图4 真值与预测值斑块区域交并情况示意图。注：为便于观察，将真值射线与预测值射线错开一定角度表示，实际二者在同一射线上Fig.4 Schematic diagram of the intersection of the true value and the predicted value patch area.Note: For the convenience of observation,the true value ray and the predicted value ray are staggered by a certain angle,and the two are actually on the same ray

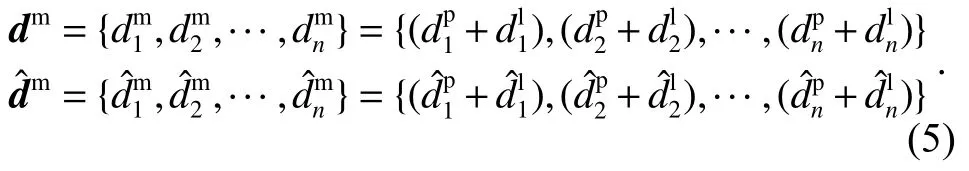
对于斑块区域真值与预测值的实际相交情况，制定如下判定原则：第i条射线上，血管区域预测值距离与真值距离中的较小值，小于管腔区域预测值距离与真值距离中的较大值时，认为斑块区域在该射线方向上不相交，反之相交。据此，斑块区域损失函数设计如下：

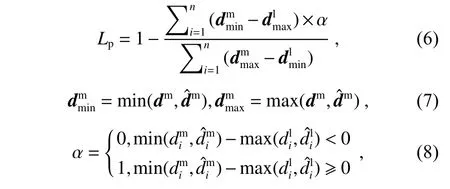
其中：n为建模过程中预设的射线数量，α表示第i(i=1,2,···,n)条射线上真值与预测值中斑块区域的二维相交情况。另外，由于斑块区域和管腔区域各自所占实际面积较小，初期收敛相对困难，为此加入血管区域损失函数Lm，以加快收敛速度。最终损失函数为管腔区域损失、斑块区域损失和血管区域损失的集合，表示为IVUS Polar IoU Loss，在公式中简写为LU。

2.4 结果重建

为便于后续观察与评价，还需对网络预测结果进行重建。本文根据预设的建模中心和射线数量，利用B 样条曲线拟合对网络预测出的一维掩膜向量进行重建，获得对应的二维管腔区域和斑块区域。

3 实验结果与分析

3.1 数据集与数据扩增

为验证所提算法的有效性，在来自4 位匿名患者的743 张临床IVUS 图像构成的数据集上进行了训练与测试评估。所有图像由市售成像系统采集，采集所用的超声换能器频率为20 MHz，采集时的检测深度为5 mm。原始图像分辨率大小为 500×500。数据集的标准管腔区域和斑块区域由两名研究人员在心血管疾病专业医生的指导下进行手动标注。考虑到数据来源受限以及相同患者间IVUS 图像的相似性，为确保算法的泛化性得到一定验证，以患者为分折依据，采用四折交叉验证作为训练与测试策略。客观评价方面，各折下验证结果评价指标以验证数据量占总数据量比例进行加权求和作为最终评价结果。患者与其图像数量关系如表1 所示。

表1 IVUS 数据集信息Table 1 Information of the IVUS dataset

为缓解模型训练过程中的训练集过拟合问题，本文对训练集进行了实时数据扩增，具体方法如下：

1) 随机翻转：包括随机水平翻转和随机垂直翻转。

2) 随机旋转：在0～360°内随机旋转一定角度。

3) 离散小波分解：将原图放大到512×512 大小，再通过离散小波分解的手段对其进行处理，将其处理为一个尺寸为256×256，通道数为4 的输入图像，每个通道分别对应离散小波处理结果的低频信息、垂直高频信息、水平高频信息和对角高频信息。

值得说明的是，前两步数据扩增的方式仅在训练时进行，而离散小波分解的处理在训练和测试时均需进行。这一处理的根本目的是进行图像缩小的同时保留原始图像的所有信息，尤其是对网络学习具有积极影响的高频部分[26]，保证IVUS 图像中的信息得到充分利用。

3.2 训练

模型训练在Windows10、Pytorch1.9.0、Python3.6的环境下进行，使用单个 NVIDIA GeForce RTX 3060 GPU 进行加速。优化器采用 AdamW，学习率设置为0.0001，训练批次大小设置为 4，根据网络宽度和深度训练200～300 个epoch 不等。

3.3 评价指标

本文采用Jaccard 测量(Jaccard measure,JM)、Hausdorff 距离(Hausdorff distance,HD)、面积比差异(percentage of area difference,PAD)[27]以及拓扑结构错误率(topology error rate,TER)[28]等4 个评价指标，对本文算法的分割性能进行综合评价。

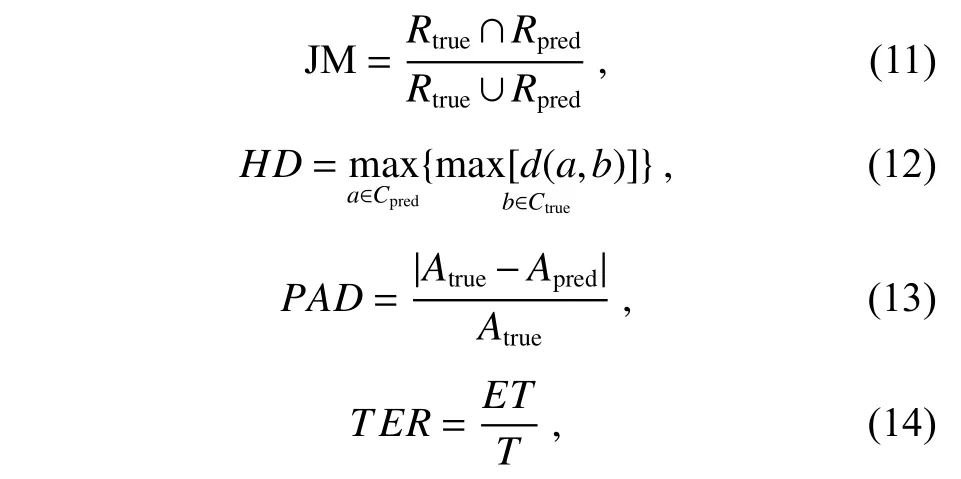
其中：JM 主要衡量分割结果和标准掩膜之间的区域差异，值越大越好。其公式中，Rtrue表示标准掩膜区域，Rpred表示分割结果区域。HD主要衡量分割结果轮廓与标准掩膜轮廓之间的差异，该结果越小越好。其公式中，a,b分别为预测结果边界轮廓Cpred上的点和标准掩膜边界轮廓Ctrue上的点。d(a,b)表示a与b之间的欧氏距离。PAD衡量的是分割结果与标准掩膜之间的面积差异，值越小越好。其公式中，Atrue表示标准掩膜的面积，Apred表示分割结果的面积。TER是衡量分割结果是否符合先验知识的重要指标，越小越好。其公式中，ET表示测试数据中具有错误拓扑结构的分割结果数量，T表示测试数据的数量。

3.4 射线数量选择与建模精度

PCM-PK 建模是将二维掩膜抽象为一维距离向量的过程，难以避免一定程度上的精度损失。其中，射线数量的选择决定了本文算法的精度上限。本文测试了从n=8到n=72 内的多个射线数量对IVUS 数据集二维掩膜的建模情况，利用JM 评估建模方式的准确度。JM 变化情况如图5 所示。

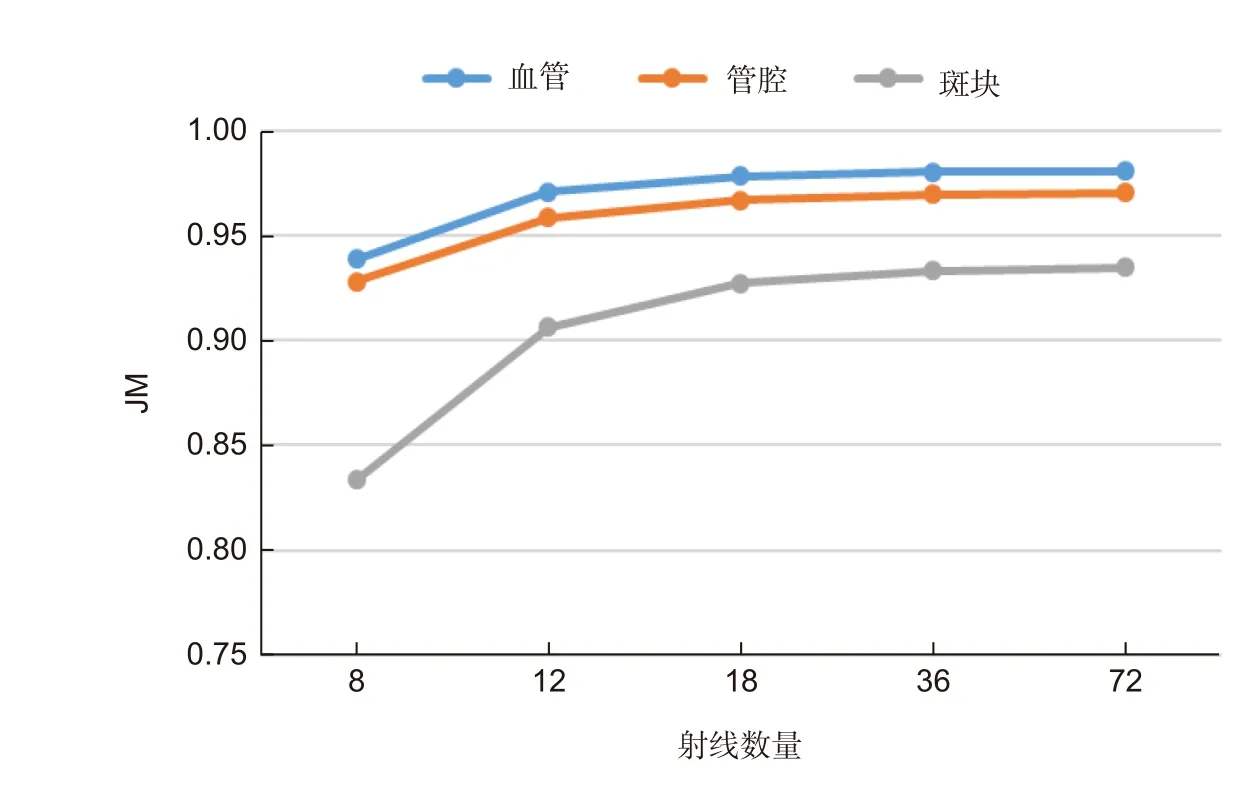
图5 JM 随射线数量变化曲线图Fig.5 The graph of JM changing with the number of rays

根据实验结果，建模准确度随着射线数量的增多而上升。当射线数量达到36 条及以上时，管腔、斑块和血管区域的建模准确度均超过0.93，重建效果良好。当射线数量超过36 条时，各区域建模准确度没有明显提升。为避免射线数量过多导致网络收敛难度加大，本文最终选择36 作为建模中预设的射线数量。

3.5 实验结果及分析

实验主要包括以下内容：比较不同深度骨架网络与不同数量SEB 模块组合的分割结果，确定最佳网络结构，并分析SEB 模块的引入对分割性能的影响；比较最佳网络结构下不同损失函数的分割结果，分析所提损失函数对网络性能的影响；比较极坐标建模与其他建模方式下的分割结果，验证极坐标建模方法的合理性；比较本文方法与其他分割网络的分割效果，验证本文算法的有效性；利用线性回归分析和Bland-Altman(BA)分析评估本文算法分割结果所提供的关键临床参数与标准掩膜所提供的关键临床参数的相关性和一致性，验证本文算法的可靠性。

3.5.1 不同深度骨架网络与不同数量SEB 模块组合的实验结果比较

为明确该密集距离回归任务对网络深度以及SEB 模块数量的实际需求，实验了多种深度骨架网络与不同数量SEB 模块的组合。一般情况下，为合理应用网络中每个block 的特征信息，当模块数量增加时，SEB 模块以深度递进的方式进行叠加。如图3 所示，当SEB 数量为1 时，仅使用SEB1，当SEB 数量为2 时，在SEB1 后叠加SEB2。当SEB 数量为3 时，将在SEB2 后继续叠加1 个SEB 模块以应用block1 提取到的特征。实验结果如表2 所示。

表2 不同深度的骨架网络与不同数量SEB 模块组合实验结果Table 2 The performance of the proposed method under different depths of backbone and different numbers of SEB modules

ResNet101 骨架网络结合2 个SEB 模块的结构取得了综合最优的效果。在血管(media)、管腔(lumen)和斑块(plaque)区域的JM 值分别达到0.8934、0.8738 和0.7430。实验结果表明，当骨架网络深度较浅时，SEB 模块的引入并无明显影响规律。当网络达到一定深度后，SEB 模块的加入表现出积极影响。分析认为，相较于深层网络，较浅的骨架网络在抽象特征的提取方面略逊一筹，即使其最深层提取到的特征信息也无法保证在关注浅层特征的同时抑制噪声干扰。但骨架网络深度并非越深越好，SEB 模块数量也并非越多越好。由于IVUS 图像信息相对单一，过深的网络结构和过多的SEB 模块也可能产生结构冗余，无法进一步提升预测性能。

3.5.2 不同损失函数的实验结果比较

根据实验一，明确最佳网络结构为ResNet101-2SEB。为验证所提联合损失函数对网络约束的有效性，分析比较了最佳网络结构下不同损失函数的实验结果，如表3 所示。其中，本文设计的联合损失函数令网络获得了最好分割效果。联合损失函数由管腔损失、斑块损失以及血管损失函数共同组成。无论缺少哪一部分，均无法获得最好的综合评价。这是因为各部分损失函数仅对其相应区域的学习方向具有约束能力，而管腔、斑块和血管区域在结构上却存在相互依赖的关系，仅考虑其中两种损失的组合无法有效保证结构间的相互关系得到有效约束。因此在该任务下，使用联合损失函数能够获得更高的综合评价。此外，无论是联合损失函数还是两两组合的其他损失函数，其综合表现均优于Smoothl1。这一结果表明，当预测结果元素之间存在相关性时，联合约束优于独立约束。

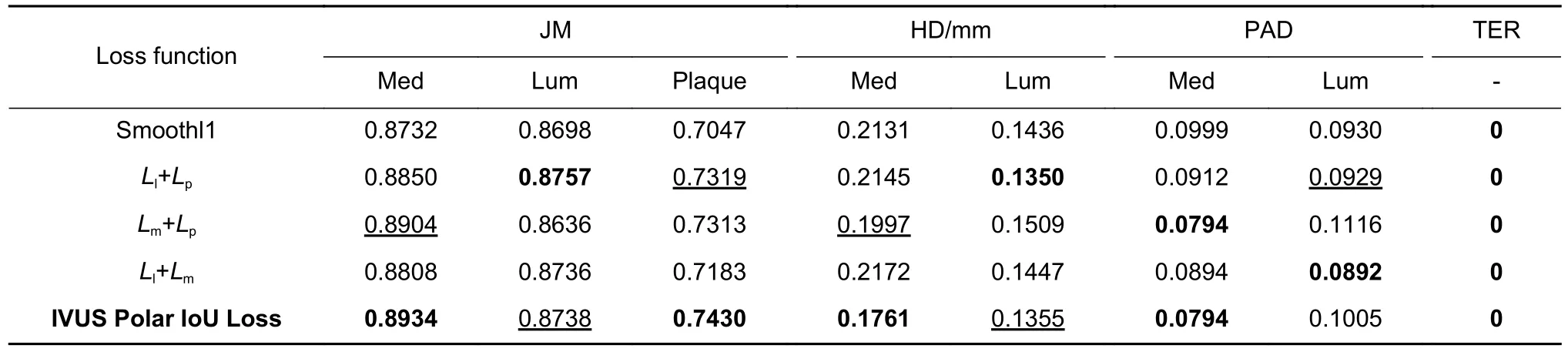
表3 不同损失函数下的实验结果Table 3 Experimental results with different loss functions

3.5.3 建模方式比较

椭圆拟合(Ellipse)是保证IVUS 分割结果拓扑结构的另一处理手段，常见于分割结果的后处理，文献[21]则将管腔与血管的椭圆拟合参数作为网络预测的直接目标。为验证极坐标建模方式的合理性，在椭圆拟合建模方式下进行网络训练并与其对比。实验使用最优网络结构与Smoothl1 损失函数，训练网络同时预测管腔和血管的椭圆拟合参数，训练策略与极坐标建模方式下相同。分割结果评价指标比较情况如表4 所示。

表4 不同建模方式下的实验结果Table 4 Experimental results with different modeling methods

PCM-PK 建模下的分割结果各指标均优于椭圆拟合的分割结果。椭圆拟合下需同时预测椭圆中心坐标、旋转角、长轴和短轴长度，导致椭圆重建结果对各参量预测结果误差敏感，造成JM 等精度评价指标不高。拓扑约束方面，椭圆拟合能够保证管腔与血管各自的拓扑结构准确，但无法实现相对位置关系的有效约束，造成部分斑块区域拓扑结构有误，如图6 所示。极坐标建模方式则解决了这些困扰，有效保留了管腔，血管以及斑块的拓扑结构。

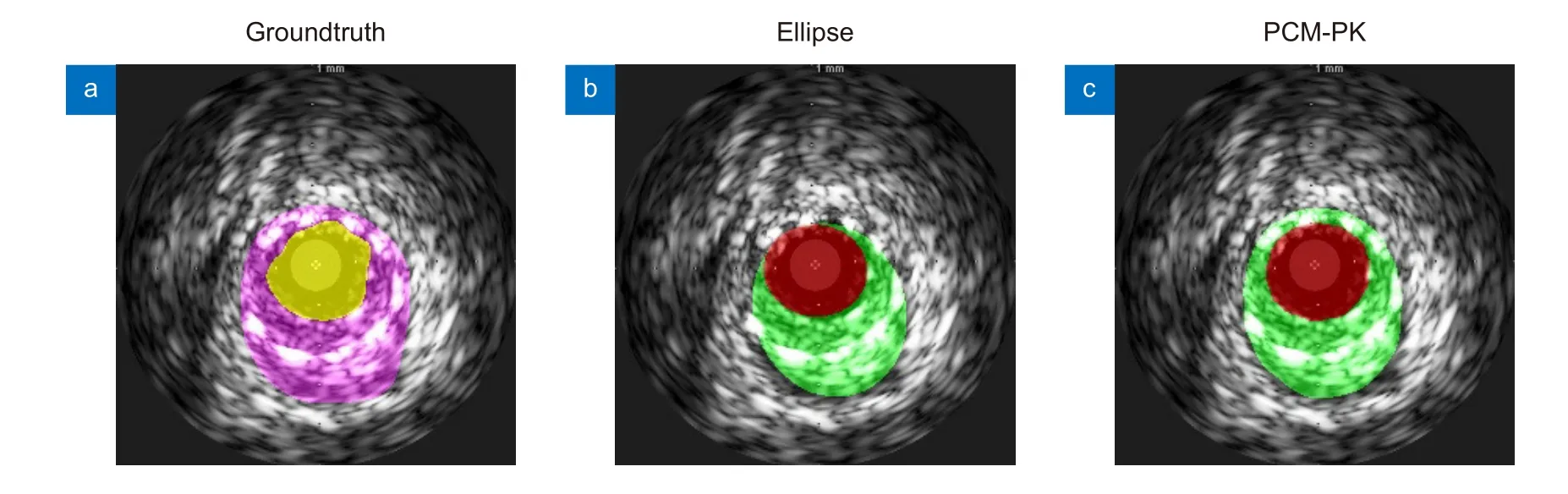
图6 不同建模方式分割结果可视化Fig.6 Visualization of segmentation results of different modeling methods

3.5.4 与其他模型比较

如表5 所示，相比于SegNet 与UNet 模型，本文算法在管腔和斑块的JM 值，管腔和血管的HD 值，管腔的PAD 值以及整体的TER 指标上的表现更加突出，尤其是TER 方面，实现了0%的拓扑结构错误率，表明所提算法的分割结果的拓扑关系完全符合先验知识。这得益于PCM-PK 建模方式对先验知识的有效编码，确保分割结果和标准掩膜具有拓扑结构一致性，解决了该任务下关注的首要问题。相比于Deeplabv3+[29]，在JM 和PAD 评价指标方面，本文算法的部分指标呈现轻微劣势，分析认为主要受到PCM-PK 建模精度损失的负面影响：抽象的表示方式造成固有损失，下降程度与建模损失成正相关。但在拓扑结构保留方面，本文算法仍占据优势。

表5 不同分割模型的性能比较Table 5 Performance comparison of different segmentation models

图7展示了标准掩膜、SegNet[30]、UNet[31]、Deeplabv3+[29]及本文算法分割结果的视觉效果对比情况。如图中箭头所指，其他基于逐像素预测的分割网络均出现了拓扑错误的问题，例如第1 行第2、3 列中出现了数量大于1 的管腔连通域和斑块连通域，第2 行第3 列出现了斑块区域的闭合环形形态被破坏，以及第3 行第3 列出现了斑块区域存在多余的孔洞等。诚然，部分拓扑错误问题可以通过一些形态学后处理方法得到解决，但是对于斑块区域的闭合形态被破坏的拓扑问题，仍没有一个通用的解决办法。而本文算法的分割结果则没有出现任何拓扑错误的问题。其中，对存在因声影或钙化影而造成局部成像缺陷的图像改善更明显，因为该算法考虑了一维向量之间的相关性，缺失部分可以通过周围没有缺陷的边缘结构进行预测。但如果缺失范围过大，导致血管区域定义模糊，算法分割性能将有所下降。此外，从视觉效果上来看，本文算法的分割结果也显示出更为平滑流畅的边缘，更符合实际血管形态。

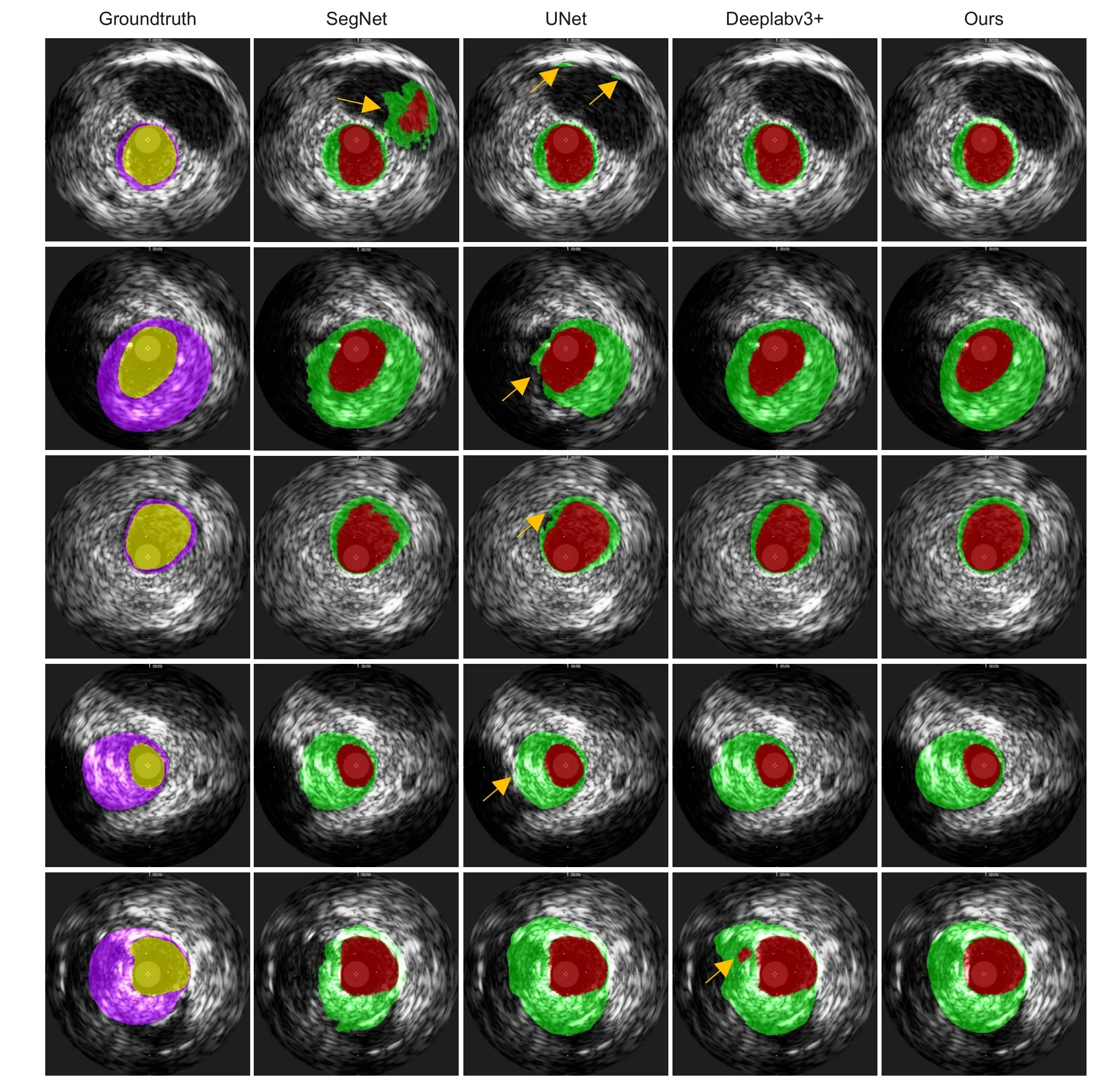
图7 分割结果视觉效果对比Fig.7 Comparison of the visual effects of the segmentation results

3.5.5 可靠性分析

IVUS 图像分割的最终目的是提供可靠的临床参数。为评估本文算法的分割结果在提供关键临床参数方面的可靠性，对所有结果进行关键临床参数计算，并与标准掩膜提供的相应参数进行线性回归分析和Bland-Altman 分析，以衡量参数的相关性和一致性。关键临床参数选择管腔横截面积(Lumen crosssectional area,LCSA)、血管横截面积(Vessel crosssectional area,VCSA)和斑块横截面积(Plaque crosssectional area,PCSA)。

关键临床参数线性回归分析如图8 所示，结果如表6 所示。LCSA、VCSA 和PCSA 的Pearson 相关系数分别为0.9427，0.9626 和0.9432，表明本文算法的分割结果能够提供和标准掩膜参数高度相关的三类关键临床参数。其中，中膜区域相关性最高，这与JM等评价指标的结果一致。

图8 关键临床参数线性回归分析Fig.8 Linear regression analysis of key clinical parameters

表6 关键临床参数线性回归分析结果Table 6 Results of linear regression analysis of key clinical parameters

Bland-Altman(BA)分析作为临床上常用的一种分析方法，能够直观反应两种测量方法的一致性程度。图9 展示了本文算法和人工标定法的关键临床参数Bland-Altman 分析，结果如表7 所示。BA 分析结果显示，本文算法对LCSA、VCSA 和PCSA 分别低估2.20%、3.56%和4.40%。分析认为，该现象主要源于PCM-PK 建模方式的固有损失趋势为重建结果面积的减小，属于建模方式造成的系统误差。但这些区域的估计误差均属于轻微偏移区间。此外，LCSA、VCSA 和PCSA 的异常值比例分别为5.25%、6.56%和7.27%，因此可以认为本文算法分割结果所提供的关键临床参数与人工掩膜的临床参数具有一致性。高度的相关性和一致性表明，本文算法能够提供可靠的关键临床参数，对心血管疾病临床诊断与研究具有积极影响。

图9 关键临床参数 Bland-Altman 分析Fig.9 Bland-Altman analysis of key clinical parameters

表7 关键临床参数Bland-Altman 分析结果Table 7 Results of Bland-Altman analysis of key clinical parameters

4 结论

针对现有分割网络无法保证IVUS 图像分割结果符合先验知识的问题，本文提出一种基于极坐标建模和密集距离回归网络的IVUS 图像自动分割方法。该方法首先利用一种基于先验知识的极坐标建模方式将IVUS 图像二维掩膜图建模为一维欧氏距离向量，然后利用一种结合了语义嵌入模块和残差网络的密集距离回归网络学习IVUS 图像与一维距离向量的映射关系，并构建了一种联合损失函数IVUS-Polar IoU Loss 约束网络学习方向。实验结果表明，相较于其他分割网络，本文算法不仅能够100%保证分割结果拓扑关系符合先验知识，并且分割结果具有良好的分割准确率和视觉效果，能够快速地提供可靠的关键临床参数作为后续诊断的参考。