横向冲击作用下圆钢管混凝土构件挠度尺寸效应研究

刘艳辉， 慈伟主,2， 赵一超， 王路明， 徐 楠， 梁嘉瑜

(1. 西南交通大学 土木工程学院, 成都 610031； 2. 安徽省交通规划设计研究总院股份有限公司, 合肥 230088)

钢管混凝土(concrete filled steel tube， CFST)结构具有承载力高、塑性好、经济方便等优越的性能，因而被广泛应用于高层、大跨和桥墩等结构中[1-3]。钢管混凝土结构在服役期间，很有可能遭受冲击荷载的作用，如列车脱轨撞击站房、船舶撞击桥墩等。冲击作为一种高频高危的极端荷载，一旦发生不仅可能对构件本身造成破坏，更有可能对整体结构造成损伤破坏，甚至引起连续倒塌。所以研究钢管混凝土构件的抗冲击性能，不仅对构件自身的抗冲击防护具有很好的实际意义，同时也对工程结构抗倒塌防护及防灾减灾等都具有重大意义。

自21世纪以来，国内外学者[4-15]对横向冲击荷载作用下的钢管混凝土结构进行了一系列研究。表1统计了近年来国内外学者进行的圆钢管混凝土构件落锤冲击试验，这些试验和研究大多都采用缩比的小尺寸模型。然而，通过对具有相似几何形状的小尺寸模型进行试验，能否确定大尺寸原型的动态响应特性，与实际工程是否存在差距，还有待验证。而目前对于钢管混凝土构件的尺寸效应研究，目前主要局限在其轴压性能上，陆新征等[16]研究了钢管混凝土短柱的尺寸效应，统计分析了252组试验数据后发现：现有的规范都未对构件的尺寸效应予以考虑，随着尺寸的增大，计算值与试验值误差逐渐增大。金浏等[17]通过建立数值模型建立了钢管横向约束作用对混凝土柱名义轴压强度及其尺寸效应的影响规律，并建立了考虑横向约束作用的混凝土柱轴压强度的尺寸效应理论公式。陈鹏等[18]对18个圆钢管混凝土柱进行了轴压试验，通过参数分析发现试件截面含钢率、钢材屈服强度及混凝土圆柱体轴心抗压强度均对峰值应力尺寸效应存在一定影响。对于钢管混凝土构件在横向冲击下的动态响应是否存在尺寸效应，目前国内外尚缺乏研究。事实上，对于大多数遭受动力荷载从而引起塑性行为的试验(如落锤冲击试验)，想要其动态响应严格遵循相似准则，是十分困难的。对于落锤冲击试验，Booth等[19]进行了13组落锤冲击试验，对1/10至全尺寸的薄板软钢结构进行了试验，结果发现全尺寸原型在落锤冲击后的无量纲挠度是缩尺系数0.25的小模型的2.5倍。Jones[20]指出落锤冲击试验中进行等比缩放时，材料的应变率敏感性、断裂、重力等情况不能进行等比缩放，因而对最终结果会产生一定的影响，即尺寸效应。为了能更好的将基于小尺寸试验的理论应用于工程实践，研究CFST构件在横向冲击试验中的尺寸效应十分重要。

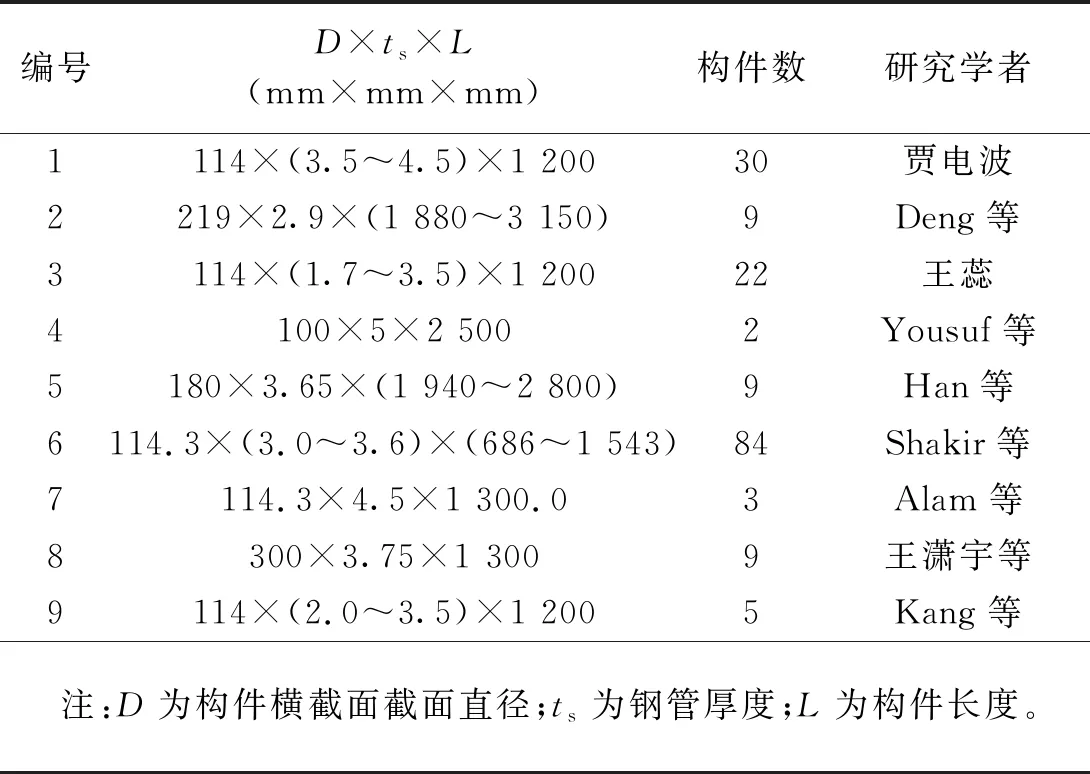
表1 统计的构件信息

本文基于相似准则，建立了圆钢管混凝土构件遭受横向冲击的相似模型，分析了冲击相似准则成立的条件。并利用有限元软件 LS-DYNA 对钢管混凝土构件在横向冲击荷载作用下的动力响应进行了数值模拟，对比分析了按照相似准则放缩的大尺寸原型和小尺寸模型构件的挠度尺寸效应，并分析了导致挠度尺寸效应的原因，对钢管混凝土构件抗冲击性能的试验研究和工程应用具有重要意义。

1 落锤冲击钢管混凝土构件的相似模型

1.1 相似模型中物理量的比例关系

为了研究横向冲击作用下钢管混凝土构件的尺寸效应，应该尽可能的保证小尺寸模型与大尺寸原型的几何相似。对于落锤冲击圆钢管混凝土的模型中相关物理量，主要基于以下两个基本条件进行分析和讨论：

(1) 满足几何相似准则，即小尺寸模型所有方向上的线性尺寸与大尺寸原型的尺寸的比例(即几何缩放系数λ)相同，为

λ=lm/lp

(1)

式中，l为长度尺寸的物理量。同时，为了满足几何相似，冲击位置在模型与原型中也应该相对应。

(2) 材料属性相同。即小尺寸模型与大尺寸原型的材料强度(fy，fc)、弹性模量(E)、泊松比(v)和密度(ρ)均相同。

基于以上两个基本条件，将根据相似准则对其他的物理量进行分析，并规定所有以p为下标的物理量为大尺寸原型的物理量；所有以m为下标的物理量为小尺寸模型的物理量，以便更好的表达。

1.1.1 质 量

根据几何相似准则和式(1)，易知小尺寸模型和大尺寸原型的体积Vm和Vp间的关系为

(2)

同时因为模型和原型的材料属性相同，密度ρ相同，可知

(3)

由式(3)可知，小尺寸模型的质量mm是中大尺寸原型的质量mp的λ3倍。

1.1.2 应 变

构件中正应变ε的定义为长度改变量δ与原长度l的比值，对于小尺寸模型，即

(4)

根据式(1)有lm=λlp和δm=λδp，代入式(4)可得

(5)

由式(5)可知，在小尺寸模型和大尺寸原型中，构件的应变是相同的，并且和材料属性无关。

1.1.3 应 力

根据虎克定律，可得应力σ和应变ε的关系如下

σm=Eεm

(6)

σp=Eεp

(7)

联立式(5)～式(7)，可知σm=σp。由此可知，在小尺寸模型和大尺寸原型中，构件的应力是相同的。

1.1.4 力

为了使构件局部平衡，施加在构件表面的力F引起的压强P应该与垂直于边界的应力σ大小相等，方向相反。于是有

Pm=-σm=-σp=Pp

(8)

根据几何相似准则和式(1)，易知小尺寸模型受力面积Sm和大尺寸原型Sp的受力面积关系为

(9)

则施加在小尺寸模型和大尺寸原型的力间的放缩关系为

Fm=PmSm=Ppλ2Sp=λ2Fp

(10)

由式(10)可知，小尺寸模型中的力Fm是中大尺寸原型的力Fp的λ2倍。

1.1.5 力 矩

力矩M的表达式为力乘以力臂，即

Mm=Fmlm

(11)

将式(1)和式(10)代入式(11)，可得

Mm=λ3Fplp=λ3Mp

(12)

由式(12)可知，小尺寸模型中的力矩Mm是中大尺寸原型的力Mp的λ3倍。

1.1.6 时 间

根据初等应力波理论，扰动在相同线弹性材料制成的几何相似的原型和模型中传播速度相同。即

cp=cm

(13)

扰动在模型和原型构件中传播对应距离的时间为lm/cm和lp/cp。因此，为了使扰动在传递对应的距离时动态响应相似，时间上应满足放缩条件

(14)

由式(14)可知，小尺寸模型的质量tm是中大尺寸原型的质量tp的λ倍。

1.1.7 应变率

应变率是表征材料变形速率的物理量，物理表达式为应变除以时间，即

(15)

将式(5)和式(14)代入式(15)，可得

(16)

由式(16)可知，小尺寸模型中的应变率是大尺寸原型中的应变率的λ-1倍。

1.1.8 速 度

速度v由位移δ除以时间t给出，即

(17)

根据式(1)有δm=λδp，将δm=λδp和式(14)代入式(17)，可得

(18)

由式(18)可知，小尺寸模型中的速度vm与大尺寸原型中的速度vp相同。

1.1.9 加速度

加速度a为速度的变化量v与发生这一变化所用的时间t的比值，即

(19)

将式(14)和式(18)代入式(19)，可得

(20)

由式(20)可知，小尺寸模型中的加速度am是大尺寸原型中的加速度ap的λ-1倍。

1.1.10 冲击能量

冲击能量由动能定理求得，即

(21)

将式(3)和式(18)代入式(21)，可得

(22)

由式(22)可知，小尺寸模型中的冲击能量Em是大尺寸原型中的冲击能量Ep的λ3倍。最终得到所有物理量在模型和原型中的比例关系，如表2所示。

表2 各物理量在模型和原型中的比例关系

1.2 量纲分析法推导相似模型

钢管混凝土在横向落锤冲击作用下的响应涉及多个物理量，可以通过量纲分析法得到各个物理量之间的关系。冲击体与钢管混凝土的相互作用示意图，如图1所示。钢管混凝土构件在冲击载荷作用下的最大挠度可作为其抗冲击性能的重要指标之一，而决定最大挠度ω的物理量主要包括：① 冲击体参数，即冲击体质量m，密度ρI，冲击面面积S，冲击速度v;② 混凝土材料属性，即密度ρc，弹性模量Ec，抗拉强度fc，泊松比μc；③ 钢管材料属性，即密度ρs，弹性模量Es，抗拉强度fy，泊松比μs；④ 构件几何尺寸，即构件横截面直径D，钢管厚度ts，冲击点距左支座距离L1，冲击点距右支座距离L2。

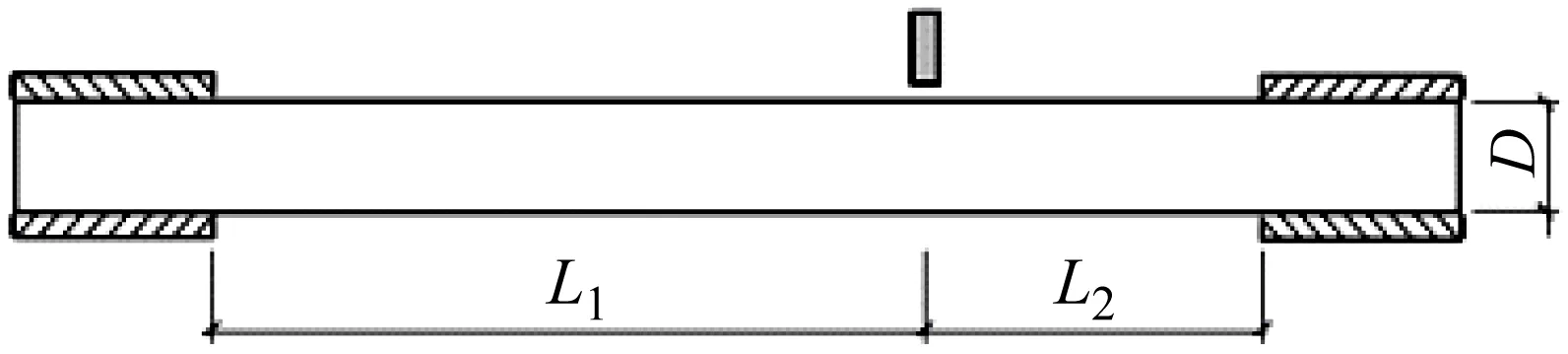
图1 落锤冲击钢管混凝土示意图

基于以上16个物理量参数，最大位移ω与各物理量之间的函数关系可写为

ω=f(m,ρI,S,v,ρc,Ec,fc,μc,ρs,Es,fy,μs,ts,

D,L1,L2)

(23)

选取构件横截面直径D、钢管弹性模量Es、钢管密度ρs3个具有独立量纲的物理参数作为基本量，根据π定理[21]，可以将式(23)改写为由13个无量纲参数决定的无量纲的因果关系

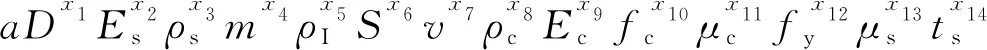
(24)

式中：a为常数；x1～x16为各物理量指数。则落锤冲击钢管混凝土的系统量纲矩阵，如表3所示。根据量纲齐次原则，可以得到3个线性齐次代数方程

表3 系统量纲矩阵

(25)

式(4)可解得

(26)

系统量纲矩阵的秩为3，则相似准则数为16-3=13。故应该前后设定13套数值，不妨设其中的一项值为1，其余相应为零，可得量纲分析π矩阵如表4所示。根据量纲分析π矩阵可得π1～π13的表达式，令π=ω/D，式(24)可化为

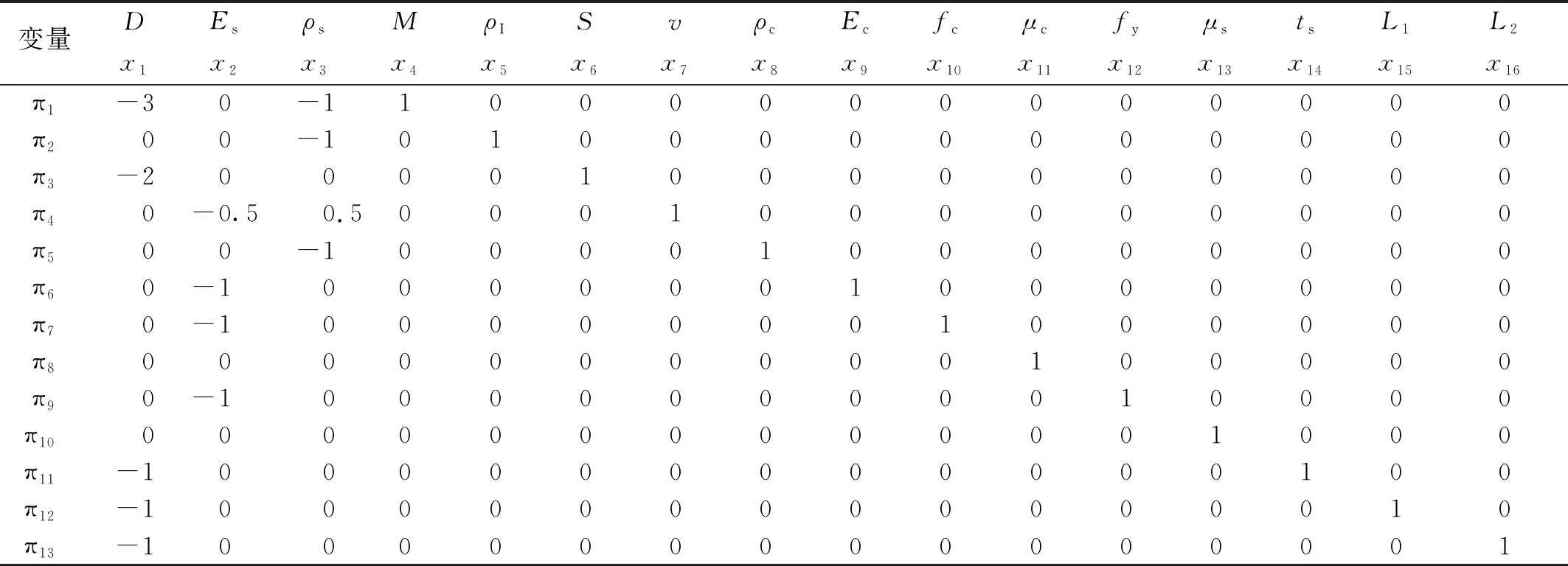
表4 量纲分析π矩阵

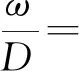
(27)

式中，a0～a13为待定实数。式(27)为此类问题的通用模型。适用于不同钢管和混凝土材料、不同几何参数、不同冲击条件下的最大挠度经验模型的建立。当试验严格按照相似准则设计，即各个物理量比例关系按照表2取值时，则原型中的无量纲挠度与模型中的无量纲挠度相等，即

(28)

即可得到几何比例为λ时，模型和原型中挠度的关系为

ωm/ωp=λ

(29)

上述相似准则是目前钢管混凝土冲击试验中用缩尺试验预测原型冲击试验，并进行后续研究的理论基础。但在冲击试验中，并不是所有的现象和参数都能严格满足相似准则，将通过数值模拟的方法分别建立相对应的小尺寸模型和大尺寸原型的建立钢管混凝土构件，研究其尺寸效应。

2 有限元计算模型

2.1 有限元模型的建立

基于有限元软件LS-DYNA对落锤冲击钢管混凝土构件开展仿真分析研究，落锤、钢管、混凝土单元属性均采用八节点实体单元SOLID164，所建立的模型如图2所示。

(a)

对于材料参数，混凝土的力学行为采用混凝土损伤模型来描述，对应LS-DYNA中072R3号材料*MAT_CONCRETE_DAMAGE_REL3，通过定义动态增强系数DIF(dynamic increase factor) (动力强度/静力强度)来考虑混凝土材料的应变率效应，应变率对混凝土动态抗压强度的影响可以在CEB-FIP模型规范[22]中找到，其中混凝土抗压强度的增强系数FCDI为式(30)

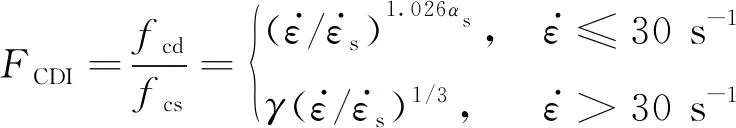
(30)

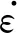
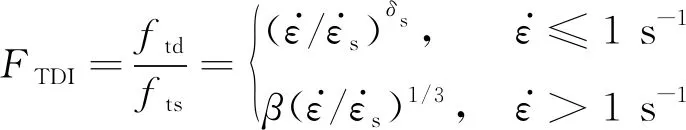
(31)

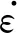
钢管的力学行为采用Cowper Symonds模型[24]来描述，对应LS-DYNA软件中的003号材料*MAT_PLASTIC_KINEMATIC，钢管的屈服强度增强系数FDIs见式(32)

(32)

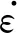
冲击体和支座均看作刚体，不考虑变形的影响，通过刚体材料*MAT_RIGID来模拟，并通过材料*MAT_RIGID关键字自带功能固定支座的各个方向的位移和转动，进而对钢管混凝土构件施加约束。通过*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE来定义冲击体与构件之间的接触、冲击体和支座之间的接触，钢管单元和混凝土单元之间设置为共节点，不考虑钢管与混凝土之间的黏结滑移。

2.2 模拟有效性验证

为了验证数值模拟所采用参数的有效性，利用Kang等研究中已有的冲击试验数据对模拟结果进行验证，试验构件信息、试验和数值模拟结果，如表5所示，验证内容为冲击时程曲线和挠度时程曲线，如图3所示。通过对比发现，各组构件的冲击力和挠度时程曲线变化趋势基本相同。最大挠度、冲击力平台值、持续时间的误差，如表6所示，均在合理范围内。综上所述，试验结果和数值模拟结果吻合的非常好，本研究所采用的参数具有有效性。

表6 仿真分析与试验结果对比

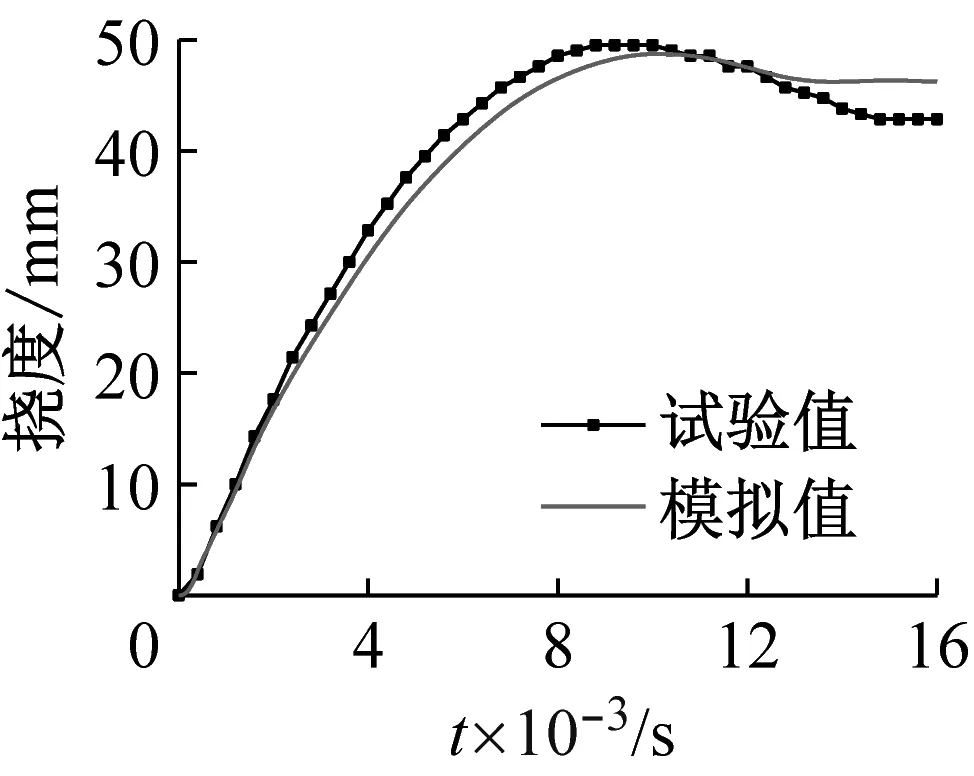
(g) YG4挠度时程曲线

3 尺寸效应分析

3.1 不同构件的尺寸效应

采用第2章建模方法，本文严格依据相似准则，建立了YG1～YG5和对应的原型构件PYG1～PYG5的数值模型(构件参数见表5)，由于YG1～YG5是按照1∶10的缩尺比例设计，根据前文的推论可知，在不存在尺寸效应的情况下，小尺寸模型的挠度和对应时间均为大尺寸原型的0.1倍，为了直观对比二者的挠度变化趋势，现在做曲线(ω/λ)-(t/λ)，如图4所示，对于未发生断裂的构件(YG1，YG4，YG5)，其小尺寸模型和大尺寸原型的挠度变化趋势基本一致(本节中的挠度和时间均指考虑几何缩放系数λ影响后的挠度ω/λ和时间t/λ)，最大挠度误差在10%以内(如表7所示)，尺寸效应较小。而对于发生开裂或断裂的构件，小尺寸模型和大尺寸原型的挠度变化趋势和动态响应则有较大的差异，在冲击过程的初始阶段，构件未发生断裂，二者挠度趋势基本相同，PYG2构件更早发生开裂，时间为47 ms，此后两构件挠度开始出现差异，YG2开裂时间为63 ms，随后YG2和PYG2构件达到最大挠度并回弹,最终趋于稳定。最大挠度误差对比未断裂构件更大，达到15.25%。对于YG3和PYG3构件，二者均发生了断裂，同样在冲击初始阶段，未发生断裂时，二者挠度趋势基本相同，而PYG3更早开裂，开裂时间为30 ms，在115 ms完全断裂，而YG3开裂时间为40 ms，在195 ms完全断裂，从构件发生开裂开始，二者挠度变化趋势明显不同，大尺寸原型构件PYG3挠度更大，随后构件发生断裂，而两者挠度差距也越来越大。在YG3发生断裂时，即195 ms时，YG3和PYG3的挠度误差达到27.77%。

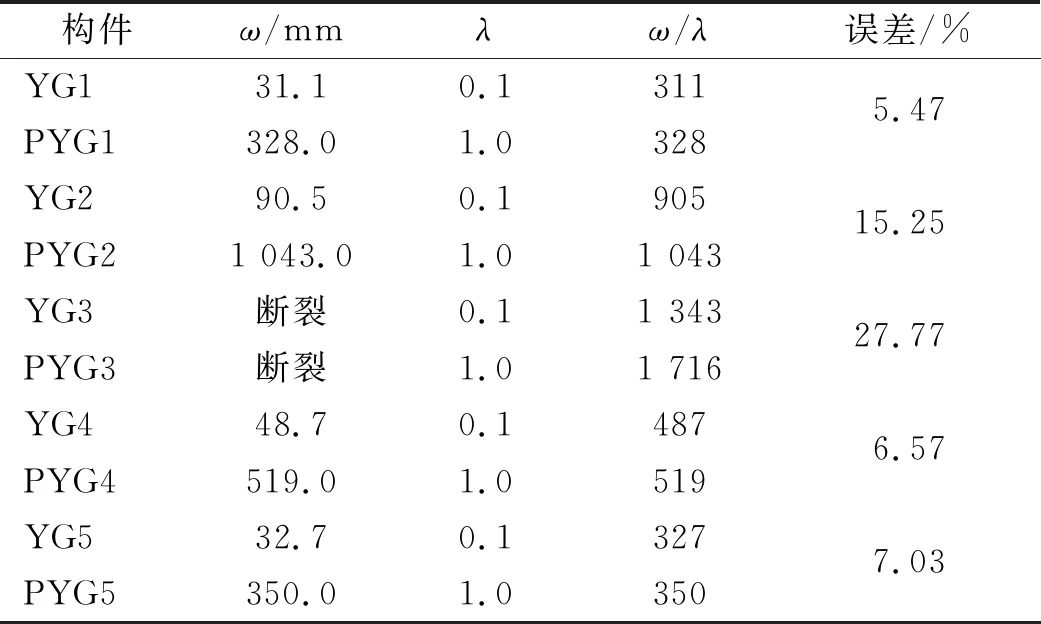
表7 最大挠度尺寸效应

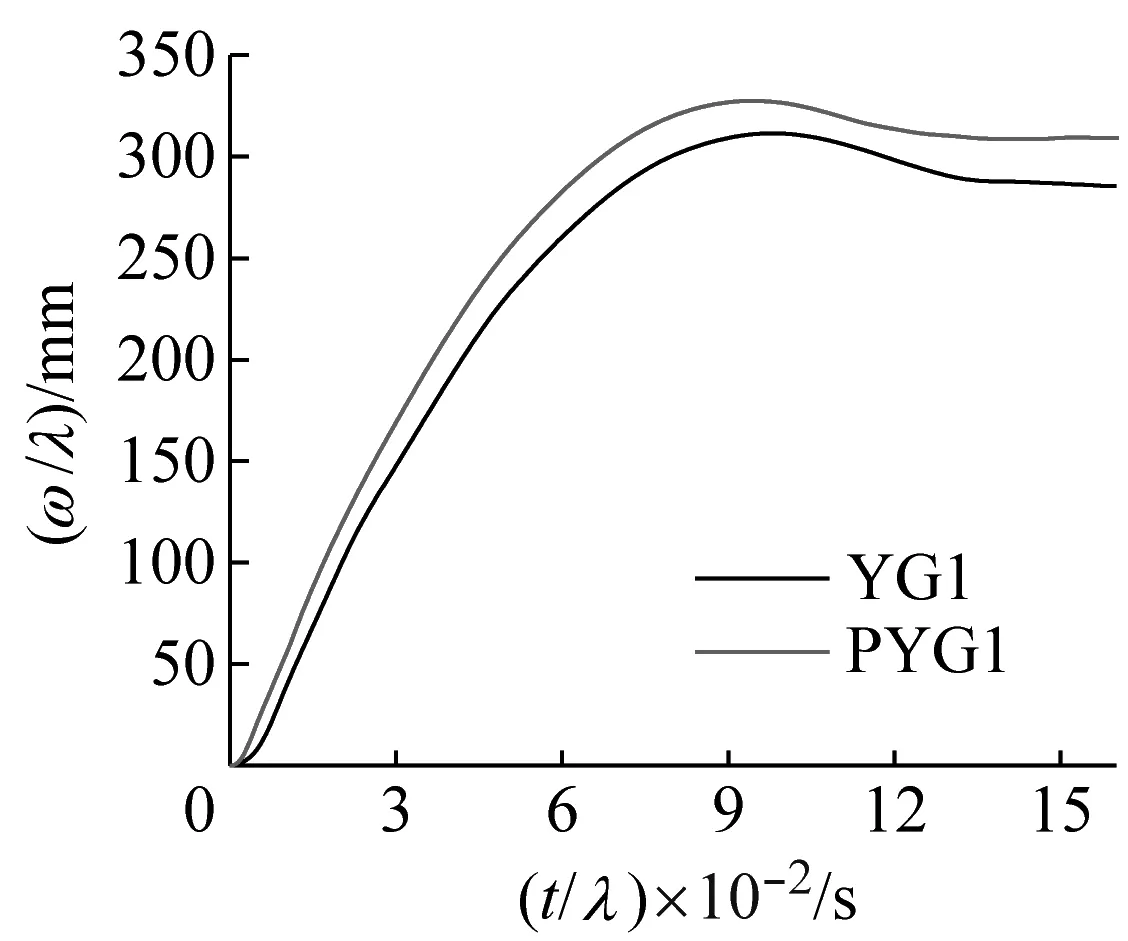
(a) YG1

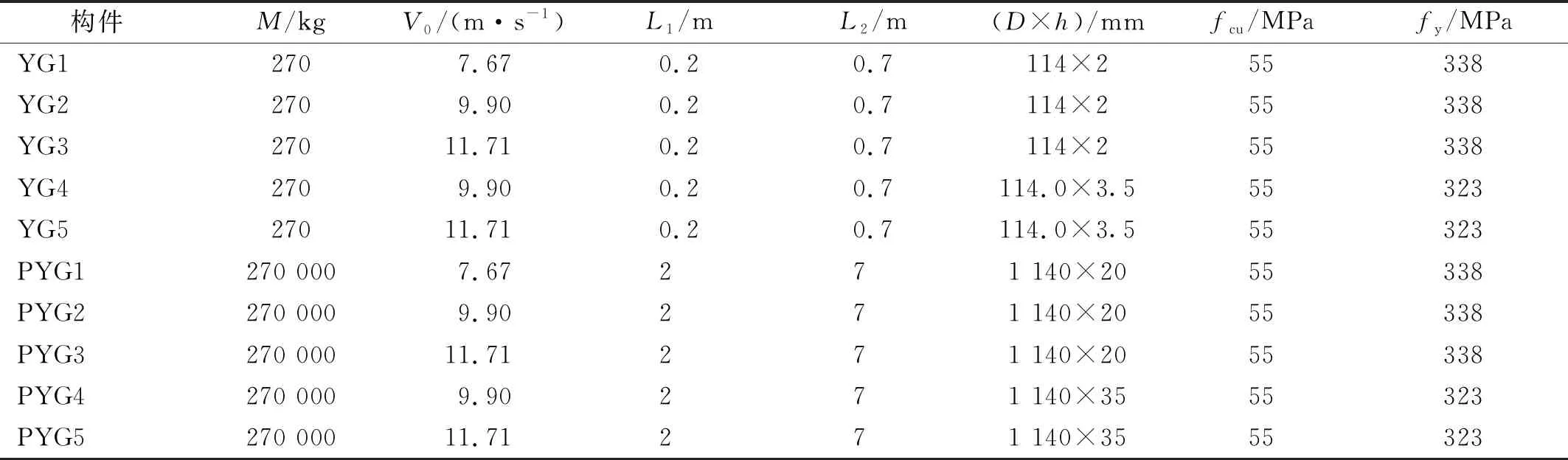
表5 算例试件信息

(a) YG1挠度时程曲线

3.2 尺寸效应原因分析

由3.1节数值模拟结果可知，相比未开裂的构件，发生开裂或断裂构件的尺寸效应更为明显。即使严格按照相似准则对表2中的参数进行设计，但仍然存在不可避免的尺寸效应。这是因为在冲击试验过程中，并不是所有的参数都能满足相似准则，Jones指出落锤冲击试验中进行等比缩放时，材料的应变率敏感性、断裂等情况不能进行等比缩放，此外，混凝土材料本身也存在一定的尺寸效应。

3.2.1 材料的动态强度

(1) 混凝土材料本身的尺寸效应

众所周知，混凝土作为一种准脆性材料，其本身存在一定的尺寸效应。Blanks等[25]系统性研究了混凝土圆柱体的抗压强度，并提出的了用于圆柱体混凝土试件的尺寸效应系数公式。

λu=1.67D-0.112

(33)

式中:λu为尺寸效应系数;D为圆柱体混凝土试件的直径，mm。由式(33)可得

(34)

对于本次研究，取λ=0.1，可得(fcd)m=1.294·(fcd)p，即小尺寸模型中的混凝土动态抗压强度比大尺寸原型中提高了29.4%。

(2) 应变率效应导致的尺寸效应

对于小尺寸模型和大尺寸原型，虽然其应变率能够满足相似准则，但应变率效应引起材料的动力强度并不能遵循相似准则，从而引起尺寸效应。在材料参数方面，混凝土的性能遵循混凝土损伤模型，并根据动态增加因子考虑混凝土的应变率效应。根据式(30)可得

(35)

对于本次研究，取λ=0.1，as=(5+9fcs/fco)-1=0.022 67，可得(fcd)m=1.055(fcd)p，即小尺寸模型中的混凝土动态抗压强度比大尺寸原型中提高了5.5%。对于钢材料，假定其力学性能遵循Cowper-Symonds本构方程，根据式(32)可得

(36)

对于本次试验，取λ=0.1，C=6 844，P=3.91，对于钢管混凝土冲击问题，其最大应变率约为1～10 s-1[26]，对于样本试验，冲击点处应变率低于3 s-1，当取应变率为3 s-1时，可得(fyd)m=1.057(fyd)p，即小尺寸模型中的钢的动态抗压强度比大尺寸原型中提高了5.7%。对于小尺寸模型，应变率效应能给材料强度的提升低于6%，因此对于未发生断裂的构件，材料动力强度带来的尺寸效应是较小的。同时，相比未断裂构件，断裂构件的应变率更大，所带来的尺寸效应也就越大，与数值模拟结果相对应。

(3) 考虑尺寸效应的挠度修正系数

为了考虑两种因素的耦合影响，现计算不同尺寸构件的塑性极限弯矩。Elchalakani等[27]提出了静力作用下塑性极限弯矩的计算方法，Qu等[28]在静力计算方法的基础上，提出的动力塑性极限弯矩的计算方法。如式(37)～式(39)所示

(37)

(38)

Myd=My×(α1×ρ1+α2×ρ2)

(39)

式中：Myd为动力下塑性极限弯矩；My为静力下塑性极限弯矩；fc为混凝土圆柱体抗压强度；fy为钢的屈服强度；D为截面直径；ts为钢管厚度；α1和α2分别为混凝土和钢的动态强度增加系数，可以由式(9)和式(11)求得；ρ1和ρ2分别为混凝土和钢管的静塑性弯矩与全截面静塑性弯矩的比值。

Qu等研究了钢管混凝土构件在横向冲击下的挠度计算公式，如式(40)所示

(40)

式中：KE为冲击体动能；L为构件净跨；Myd为动力下塑性极限弯矩。通过式(40)有

(41)

将式(34)～式(39)代入式(41)，并结合表2中的几何放缩关系，可得挠度修正系数ξ为

(42)

式中：ρ1和ρ2分别为混凝土和钢管的静塑性弯矩与全截面静塑性弯矩的比值；λ0，λ1和λ2为材料强度修正系数，按式(34)～式(36)计算。

对于未发生断裂的构件，利用式(42)即可以通过小尺寸模型的挠度ωm来预测大尺寸原型的挠度ωp。

为了验证计算方法的有效性，建立了λ分别0.1，0.2，0.33，0.5，0.75 5种比例的算例，提取构件最大挠度，并利用上述方法计算原型构件的挠度，计算结果如表8所示。由表8可知，修正后的原型挠度与数值模拟得到的原型挠度的误差非常小，均在4%以下，证明修正系数能有效的减小尺寸效应带来的影响，通过小尺寸模型构件的挠度，即可较为准确的预测大尺寸原型构件的挠度。

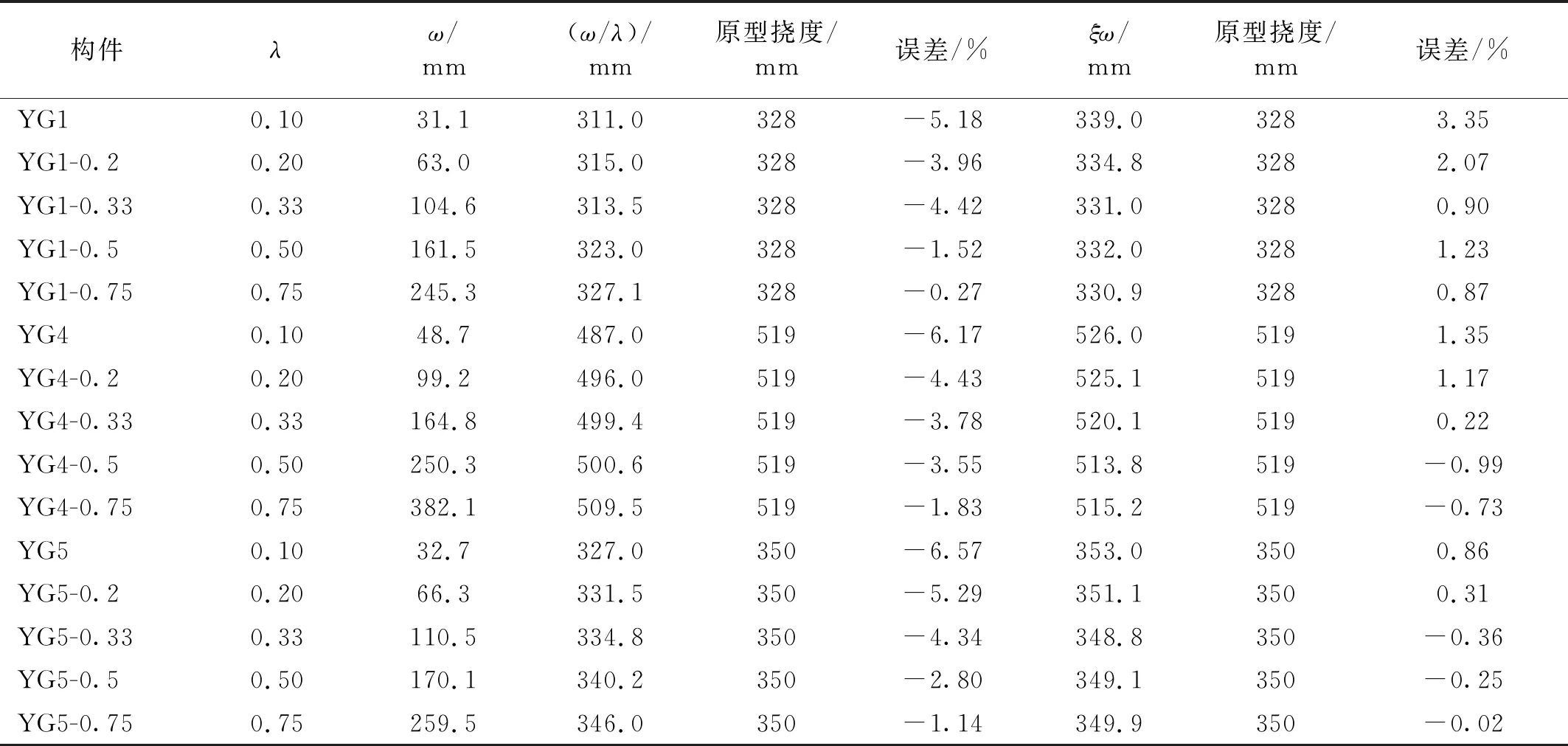
表8 未断裂构件的挠度预测

3.2.2 材料的断裂应力

对于发生断裂的构件，Mai等[29]导出了控制含裂纹结构非线弹性行为的缩放律，其断裂应力满足关系

σm/σp=λ-n/(n+1)

(43)

式中，n为非线性度，当n=1时，即为线性材料的断裂应力关系

σm/σp=λ-1/2

(44)

式(44)显然不符合基本相似准则。对于本次试验，取λ=0.1，材料的断裂应力之比大于3.16，这显然不符合相似准则中应力相同的放缩律。因此在大尺寸结构中，引起断裂的应力显然小于小尺寸结构，也对应了数值模拟中，大尺寸构件比小尺寸更早开裂的现象(见图4(b)和图4(c))。同时，这也是导致断裂构件(YG2，YG3)的尺寸效应要大于未断裂构件(YG1，YG4，YG5)的原因。

4 结 论

本文依据相似准则，建立了钢管混凝土遭受横向冲击的相似模型，确定了各个参数间的放缩比例关系，同时利用LS-DYNA有限元分析软件建立了钢管混凝土受横向冲击作用的有限元模型，对横向冲击下钢管混凝土构件挠度尺寸效应进行了分析研究，对于此类构件，可以得出以下结论：

(1) 对于严格按照相似准侧进行参数设计的构件，当构件未开裂时，其模型构件和原型构件的挠度变化趋势基本一致，最大挠度误差在10%以内，尺寸效应较小。当构件发开裂或断裂时，由于其裂缝发展难以满足相似准则，故尺寸效应明显。对于开裂构件其最大挠度误差可以达到15%以上，对于完全断裂构件，尺寸效应更为明显。

(2) 混凝土材料强度本身具有的尺寸效应和应变率效应的耦合作用会导致材料的动力强度不同，继而导致塑性极限弯矩的尺寸效应，最终导致挠度的尺寸效应。对于未断裂的构件，考虑尺寸效应的影响，提出了修正系数ξ，通过模型构件的挠度，即可预测原型构件的挠度。

(3) 断裂应力不能按照相似准则放缩是导致钢管混凝土构件在横向冲击下挠度尺寸效应的重要原因，小尺寸构件所需的断裂应力可以达到大尺寸构件的3倍以上，因此大尺寸构件更早也更容易发生断裂。