红砂岩粗粒土动力试验及颗粒破碎模型研究
2023-02-22张同文张家生肖源杰
龙 尧, 张同文, 张家生, 肖源杰
(1.湖南高速铁路职业技术学院 铁道工程学院,湖南 衡阳 421002;2.中南大学 土木工程学院,长沙 410075)
红砂岩粗粒土一般形成于白垩纪或者第三纪,广泛分布于我国华北、华东、中南以及西南地区。随着我国高速铁路建设的飞速发展,线路不可避免会通过红砂岩地区。为了避免大量弃土造成环境污染和解决路堤填料缺乏问题,红砂岩不可避免的被用作为铁路路基的填料。红砂岩在列车荷载作用下会产生动力变形和颗粒破碎,对列车稳定运营产生影响。因此,针对红砂岩粗粒土的动力学特性和颗粒破碎模型的研究,显得十分具有必须性。
针对红砂岩动力学特性的研究,目前研究方式主要从温度环境、干湿循环、加载路径、能量耗散等几个方面进行。杨阳等[1]采用分离式霍普金森压杆(split hopkinson pressure bar,SHPB)试验进行红砂岩负温试验时,发现其动态强度与冻岩的静载试验完全不同。红砂岩的动态强度随温度降低呈先增后减的变化趋势。杜彬等[2]利用SHPB试验对干湿循环下的红砂岩动态拉伸力学性能进行了探讨。研究结果发现不同加载速率下红砂岩存在一个临界加载速率。当加载速率小于临界值时,动态拉伸强度随加载速率的增加而提高;当超过临界值时,动态拉伸强度保持稳定。当加载速率一定时,动态拉伸强度随干湿循环次数的增加而逐渐下降,下降速度先快后慢。张慧梅等[3-4]对红砂岩进行冲击压缩试验时发现,动态加载下红砂岩原有结构中的孔隙很难密实,动态曲线没有显著的密实段,且饱和试样在峰后段出现特殊的软化特性。低速率扰动冲击试样破碎程度较未扰动和高速率扰动更为严重,耗散能和能量耗散密度高于较高速率扰动冲击,低速率扰动冲击下试样的能量利用率更高。金解放等[5]采用动静组合加载试验装置对红砂岩破碎和能耗进行了研究。研究发现,冲击荷载下无轴压时的红砂岩试件属于张拉破坏,有轴压时的红砂岩试件属于剪切破坏。试件耗散能随冲击速度的提升呈二次函数关系递增,而轴向静应力越高,递增幅度越小。周科平等[6]基于核磁共振技术研究了红砂岩孔隙结构演化特性。微波作用过程中,红砂岩体内部产生热应力差,内部孔隙度增大、超声波波速减小、单轴抗压强度减小。随着微波功率增大,岩体孔隙结构及强度劣化程度加大。卢振宇等[7]针对红砂岩和石灰岩在不同应变率下的压缩特性,开展了动态压缩对比试验。研究发现,在冲击荷载作用下红砂岩破碎为粉末,而石灰岩破碎呈多碎块。红砂岩试件在冲击速度足够大时,应力值会直接达到破碎阈值而破碎,并非随能量累积产生累进式破坏。
动力荷载下红砂岩粗粒土会产生破碎,导致原始级配发生改变,进而影响土体本身的物理、力学性质。许多学者针对常见粗粒土建立了考虑颗粒破碎的演化模型。郭万里等[8]基于土体两参数级配方程,将级配曲线定量表示为两参数的函数,建立了反映粗粒土在剪切过程中颗粒破碎演化规律的数学模型。蔡改贫等[9]针对岩石内部颗粒非均匀性分布、聚集的特点,采用岩石轴压破碎试验和岩石岩相分析试验,基于黏结键断裂判据,构建了反映岩石内部特征的多尺度内聚颗粒模型及其颗粒破碎演化模型。丁建源等[10]引入存活概率与破碎概率比值,采用对数几率回归方法,构建了基于对数几率回归的颗粒级配曲线演化模型。该模型能较好的对颗粒级配的演化中间过程进行预测。童晨曦等[11]基于两参数Weibull分布函数,提出了有效破碎概率概念,构建的Markov破碎模型能较好地描述多粒径组颗粒破碎演化规律。Das等[12]基于超塑性方法研究了道砟粗颗粒材料的颗粒破碎演化规律。Chen等[13]分析了残积土剪胀变形随颗粒破碎时间效应变化的规律。张宗堂等[14]开展了红砂岩室内静态与扰动崩解试验,基于Weibull分布建立了红砂岩颗粒崩解破碎级配曲线演化模型。董宗磊等[15]针对传统数值方法中子颗粒数量和粒径分布选择较为主观的不足,基于Hill分布函数构建了反映不同粒径组颗粒破碎演化规律的级配转移矩阵。
从上述研究成果可知,针对红砂岩粗粒土在循环动力荷载下的动力特性研究较少,尤其是红砂岩在反复动荷载作用下的颗粒破碎演化规律更少有研究。因此,本文采用大型三轴试验针对红砂岩粗粒土的动力特性以及破碎规律展开研究,在研究粒径大小、加载次数对粗粒土动力响应和颗粒破碎影响的基础上,构建了动力破碎概率密度函数f,并基于Markov链建立了颗粒破碎模型,期望能为红砂岩地区的铁路路基填料设计、施工以及运营监测提供理论依据。
1 试验材料、设备及方案
根据TB 10001—2016 《铁路路基设计规范》[16],实际工程中路基颗粒材料填料宜选用A、B组填料和C组碎石、砾石类填料,且路基基床以下部位填料最大粒径不宜大于300 mm。填料大多是由大小不同粒径颗粒组成,相比单一粒径颗粒,多粒径组颗粒自身性质过于复杂,比如颗粒大小,颗粒形状,风化程度等,很难分别研究每个粒径组颗粒的破碎规律。从单一粒径开展试验研究,有助于简化研究难度,为开展多粒径组破碎规律研究提供重要参考。制成单一粒径的红砂岩颗粒为不良级配,根据规范分类应为B级填料。
1.1 试验仪器
本文针对粗粒土进行动力颗粒破碎研究,考虑颗粒尺寸效应的影响,需要采用大直径试件筒的动三轴仪。为了避免颗粒尺寸效应的影响,获取真实可靠的数据,文中采用中南大学高速铁路建造技术国家工程实验室TAJ-2000大型动静三轴试验仪[17]进行红砂岩粗粒土的动强度特性研究,该三轴试验仪容许进行试验的最大粒径为60 mm,如图1所示。

图1 大型动静三轴试验仪
1.2 试验材料及方法
本文红砂岩粗粒土材料采自湖南长沙地区。采用室内动静三轴仪进行研究时,考虑消除尺寸效应的影响,一般试样直径大于材料最大粒径的5倍~6倍[18],本研究取倍数6,试件直径为300 mm,控制粒径大小为50 mm。综上考虑,为了研究粒径大小对颗粒破碎的影响规律,本文取3种单一粒径粗粒土,分别为D=31.5~45.0 mm,D=16~25 mm以及D=7.1~16.0 mm。对所采用红砂岩进行了比重瓶法和搓条法等,得到了土粒比重和液、塑限等物理参数,红砂岩相关物理力学参数具体数据,如表1所示。

表1 红砂岩物理力学参数
本文主要为了探讨红砂岩粗粒土动力条件下的破碎规律,要求在制样时不产生或者极少产生破碎,从而避免影响试验结果。根据TB 10001—2016 《铁路路基设计规范》,碎石类土路堤填料压实标准可采用孔隙率控制,其中规范要求孔隙率n(%)≤32,因此文中采用控制孔隙率的方法进行制样。红砂岩粗粒土采用天然状态含水量率进行制样,进行不排水三轴试验。试样时固结比为1.0,固结2 h,设计孔隙率为30%。

图2 振动成型过程
对于动力稳定状态,文献[19]认为稳定的标准为:若振动次数超过30 000次,塑性变形与振动次数的关系曲线趋于平缓,塑性变形的增量在作用2 000次内小于1 mm(轴向塑性应变εd<0.17%)。综合考虑,为了研究红砂岩粗粒土的动力特性以及方便数据分析,本文的荷载作用次数分别取5 000次、10 000次、20 000次、30 000次、40 000次以及50 000次。
根据现有文献研究成果,路基基床底层和路基本体填料动荷载作用主频在2~8 Hz[20],其中高速列车荷载的作用频率在2.5 Hz左右[21]。为方便研究动力特性以及后续的颗粒破碎规律,本文列车荷载取频率3 Hz。根据文献[22]对路基动应力分布情况的研究,路基基床部分的动偏应力为40~100 kPa,本文取100 kPa;粗粒土路基填料处于基床顶层以下,即约1 m深度以下。研究的路基深度范围为3~5 m,对应围压为60~100 kPa。文中取路基深度4 m为代表值,对应围压80 kPa。考虑轨道板和基床上部的质量,拟定动三轴试验静偏应力为20 kPa。
综上所述,动三轴试验参数为:围压σ3为80 kPa,动幅值σd为100 kPa,荷载频率v为3 Hz,初始静偏应力σs为20 kPa,动力试验方案如表2所示。半正弦波能较好的模拟列车荷载的作用波形[23],因此文中动三轴试验采用半正弦波形式进行加载,如图3所示。
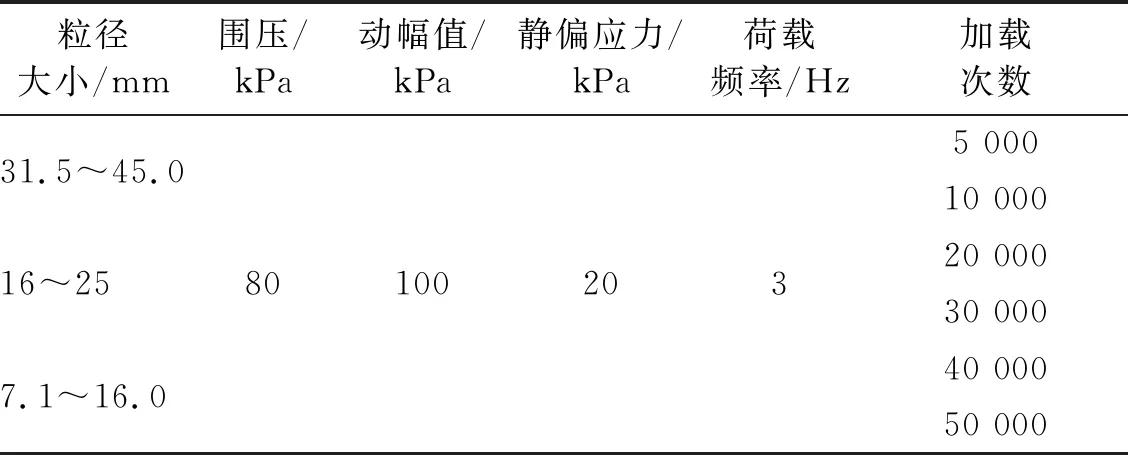
表2 动力试验方案
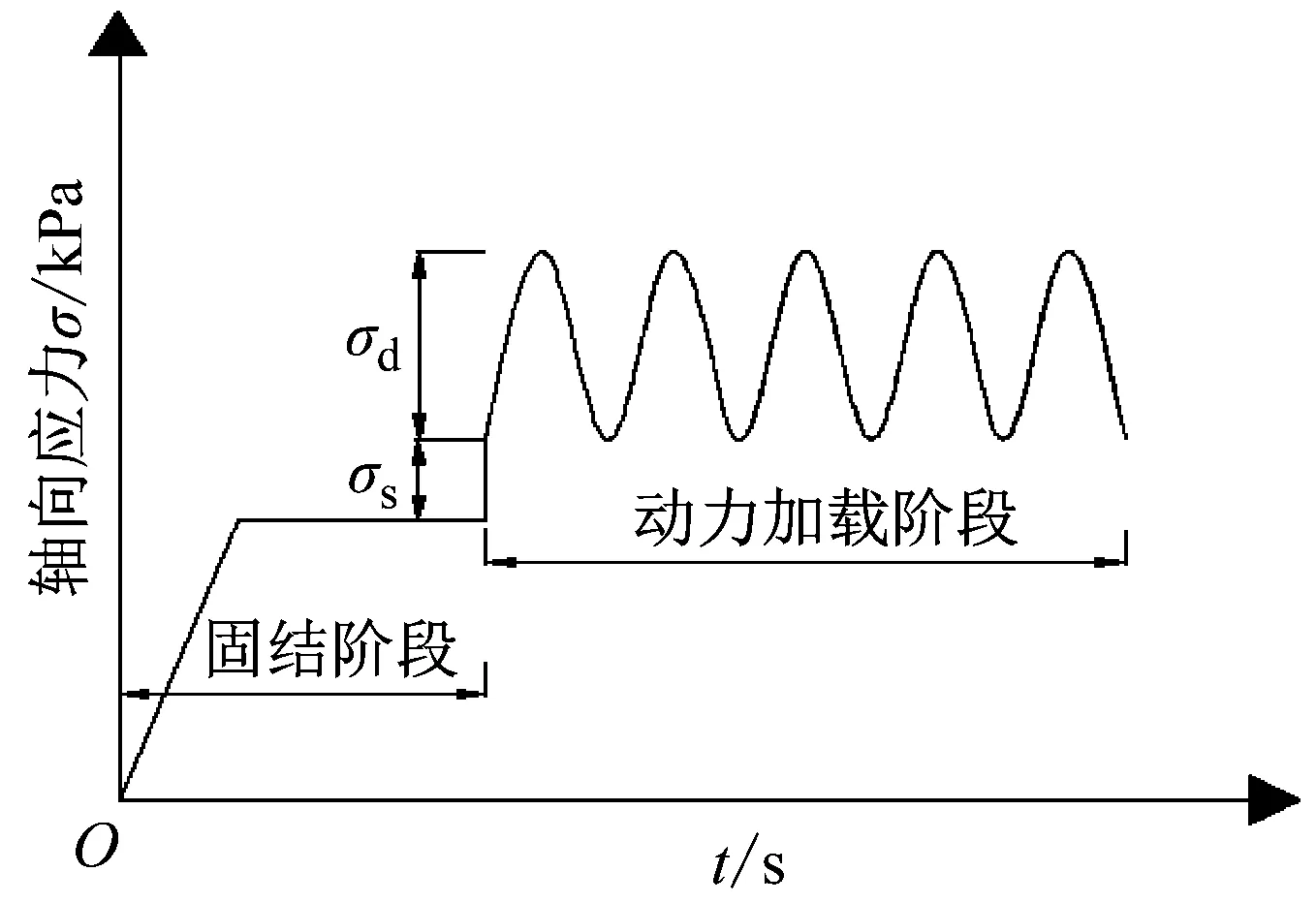
图3 动力方式加载示意图
2 试验结果及分析
2.1 粒径大小对动力变形的影响
红砂岩动力变形与颗粒破碎的程度有很大关系,为了表征颗粒破碎程度,本文采用Marsal[24]提出的Br值表征颗粒破碎率。采用试验前、后各粒组的含量差值W,然后取W的正值之和,如式(1)
Br=∑ΔWk
(1)
式中:Br为破碎率,%;ΔWk=Wki-Wkf,Wki为试验前粗粒土级配曲线上某粒径组的含量,%,Wkf为试验后粗粒土级配曲线上某粒径组的含量,%。
为了研究粒径大小与轴向应变、颗粒破碎之间的关系,采用动三轴试验得到三者之间的关系曲线,如图4和图5所示。从图4可知,整体上颗粒粒径越小,相同加载次数下轴向应变越小。当加载次数为50 000次时,31.5~45.0 mm粒径组的轴向变形值为8.7%,而粒径组7.1~16.0 mm轴向变形值仅为7.2%,31.5~45.0 mm颗粒在50 000次的轴向应变为7.1~16.0 mm的1.3倍左右。同时,图5可以得出,随着颗粒粒径的减小,颗粒破碎率随之减小。31.5~45.0 mm粒径颗粒在加载次数为40 000次时,颗粒破碎率开始趋于稳定,50 000次加载对应的破碎率为36.2%;另外,16~25 mm和7.1~16.0 mm粒径颗粒在加载次数为20 000次时,颗粒破碎率逐渐趋于稳定,50 000次加载对应的颗粒破碎率分别为25.8%和23.2%。说明小粒径颗粒土体颗粒破碎相较大粒径颗粒土体易于趋于稳定。
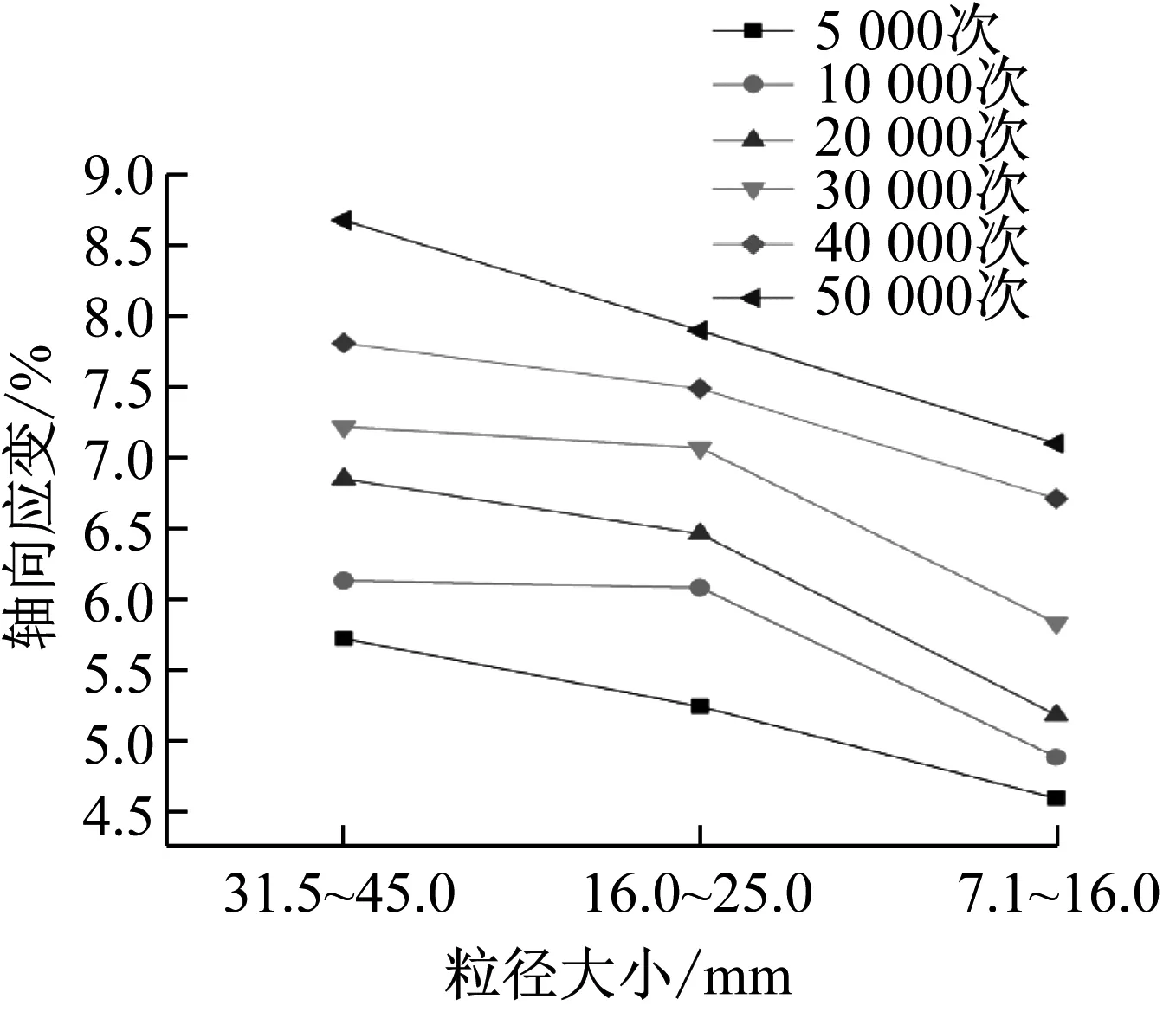
图4 粒径大小与轴向应变的关系
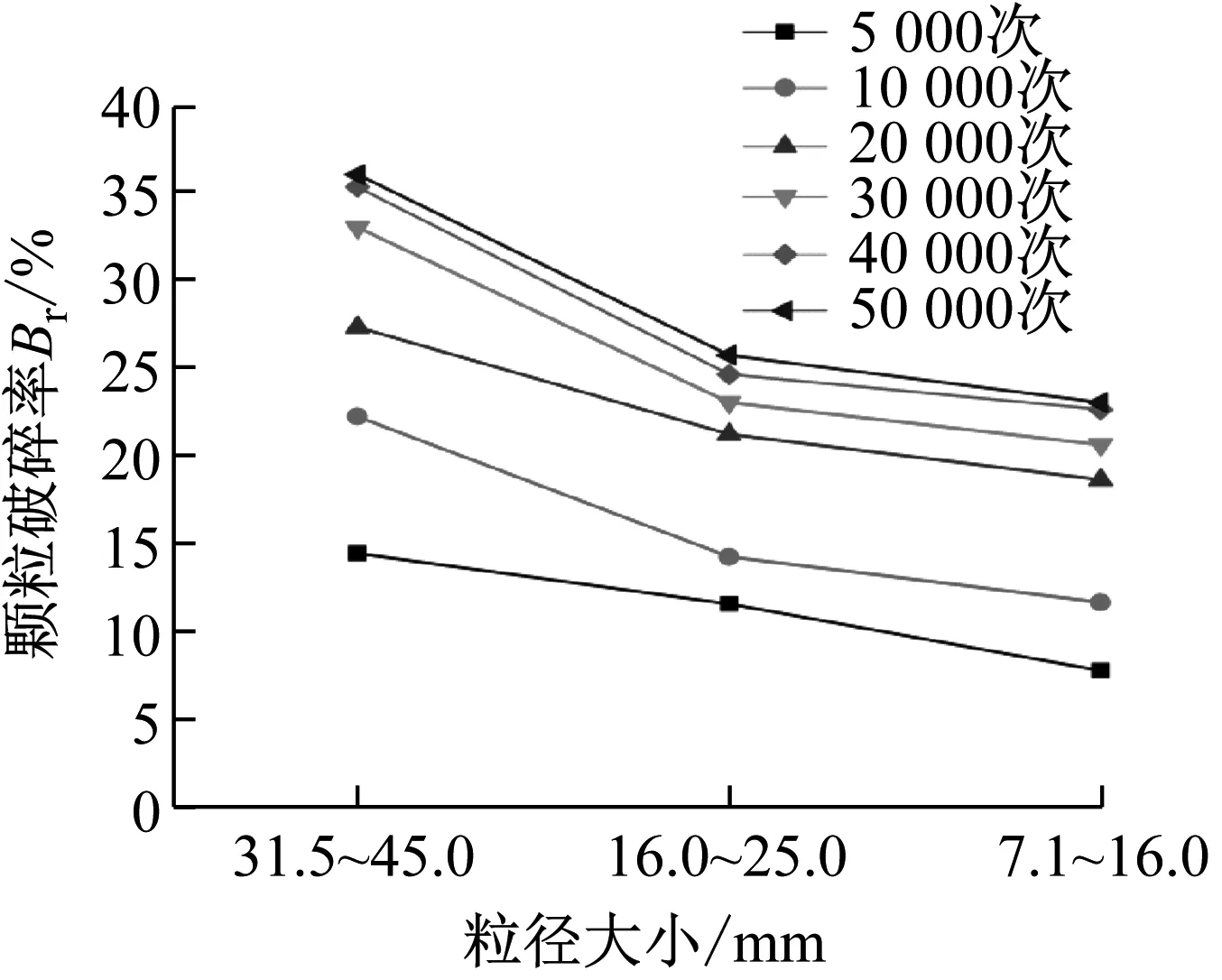
图5 粒径大小与颗粒破碎率Br的关系
此外,结合图4和图5可以得到颗粒破碎情况下动力变形主要原因为:粗颗粒土的接触方式主要为点-点接触,土颗粒所承受的平均应力与接触点的数量有关,单位体积的土颗粒粒径越小,其比表面积越大。因此大粒径土颗粒相较小粒径土颗粒,其比表面积较小,接触点数也相对较小,使得大粒径土颗粒承受的平均应力较大,从而更容易破碎。
2.2 应变软化分析
动三轴试验过程中,发现颗粒在不断破碎的同时,土体也在发生应变软化。本文的材料处于干燥状态,应变软化主要循环荷载作用下的主应力方向不断改变导致土体结构重塑,引起应变软化。参考Idriss等[25]对动力软化指数的定义,本文动三轴试验采用应力控制模式,故新定义动三轴试验条件下的软化系数,如式(2)
(2)
式中:Gs1和Gsn分别为第1次和第N次的割线动应变率;εdn和εd1为作用次数Nn和N1对应的累积动应变。加载次数与软化系数的关系,如图6所示。软化系数为累积轴向应变曲线上作用N次的割线斜率与作用第1次的割线斜率的比值。软化系数越小说明土体初始轴向应变越大,颗粒破碎程度越大,曲线初始割线斜率相对较大,而加载后期轴向应变相对较小,颗粒破碎程度越小,曲线割线斜率较小。
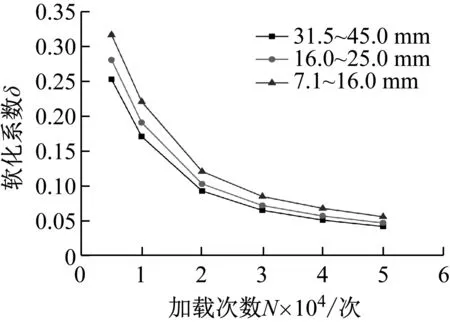
图6 加载次数与软化系数δ的关系
从图6可知,在加载初期软化系数衰减较快,当加载达到20 000次后,软化曲线逐渐趋于平缓。说明,20 000次之后大部分的颗粒破碎已经完成,土体结构重新分布基本完成。此外,随着加载次数的增加,粗粒土土体的软化程度越高,两者成半对数曲线形式,这与Matasovic等[26]研究的黏土软化指数随加载次数增加而线性减小结果不同。这是因为粗粒土在颗粒破碎过程中,级配产生自适应调整,试样结构强度不断趋于稳定,软化系数并不会呈线性持续衰减,而是呈半对数曲线并趋于一个极限值。
此外,当加载次数一定时,随着粒径的增大,软化系数越小,说明大粒径颗粒相对小粒径颗粒初期破碎更快,初始轴向应变较大。而随着加载次数的增大,不同粒径的软化系数之间的差值减小,软化系数趋于稳定值,说明加载后期不同粒径大小的颗粒都基本破碎完成,累积应变曲线趋于缓和。
2.3 土体级配和破碎率变化分析
2.3.1 级配变化分析
动力作用下红砂岩粗粒土不断破碎,土体级配发生变化。对不同荷载次数下的土体进行筛分,得到加载次数与各档粒径质量百分数的关系,如图7所示。从图7可知,动力荷载作用下,随着加载次数的增加,最大粒径档的质量百分含量减小;其余粒径档的细颗粒质量百分数随着加载次数的增加而增加,但是当增加到一定程度时,颗粒含量保持稳定,不再大幅增长,存在一个极限含量。动力荷载作用下,大粒径的破碎量主要分配到下一级粒径当中,其余较小粒径的分配比例较少。说明在动力作用下,颗粒破碎初始状态在不断演变,初始粒径在动力下产生细小颗粒以及大部分本体,这部分细小颗粒来源于颗粒边角的断裂以及颗粒表面的研磨。随着加载次数不断增加,大粒径颗粒除了不断磨耗和边角断裂,其本身内部先天缺陷——裂缝不断发生,使其主要断裂成下一级的粒径档。
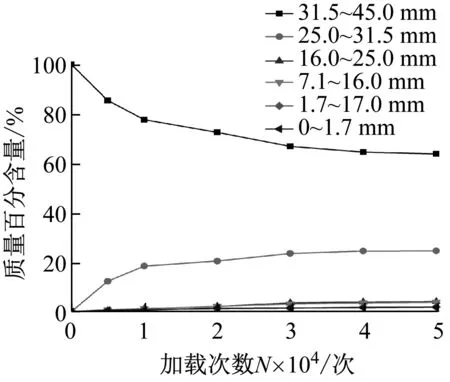
(a) 粒径31.5~45.0 mm
2.3.2 颗粒破碎率变化分析
不同粒径颗粒破碎率Br变化情况,如图8所示。从图8可知:粒径越大对应的破碎率越大,随着荷载作用次数的增加,31.5~45.0 mm的破碎率与其他两组粒径破碎率值差值变大。7.1~16.0 mm和16~25 mm粒径达到20 000次的时候,曲线出现拐点,颗粒破碎率基本完成70%;而31.5~45.0 mm的粒径达到30 000次之前,曲线基本为直线,30 000次时才出现拐点,说明在其他同等试验条件下,大粒径破碎状态达到稳定相比小粒径需要更大的加载次数和作用功,大粒径破碎后级配达到稳定需要更长时间。
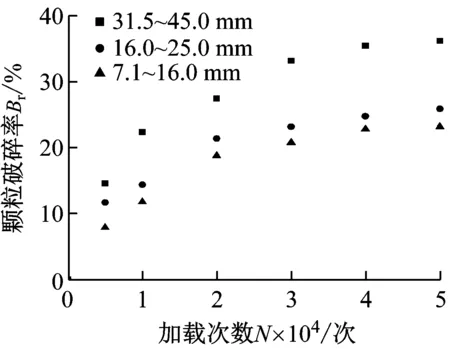
图8 不同粒径颗粒破碎率Br变化情况
7.1~16.0 mm和16~25 mm粒径的作用次数达到20 000次之前,颗粒破碎增长率较大;当作用次数超过20 000次后,颗粒破碎率趋于稳定,破碎率增长率减小,31.4~45.0 mm 的颗粒破碎率稳定在35%,16~25 mm和7.1~16.0 mm的破碎率稳定在24%。说明动力作用下,红砂岩粗粒土不是永无止境的破碎,在级配演化过程中存在一个极限级配。
3 颗粒破碎演化模型
3.1 动力破碎函数构建
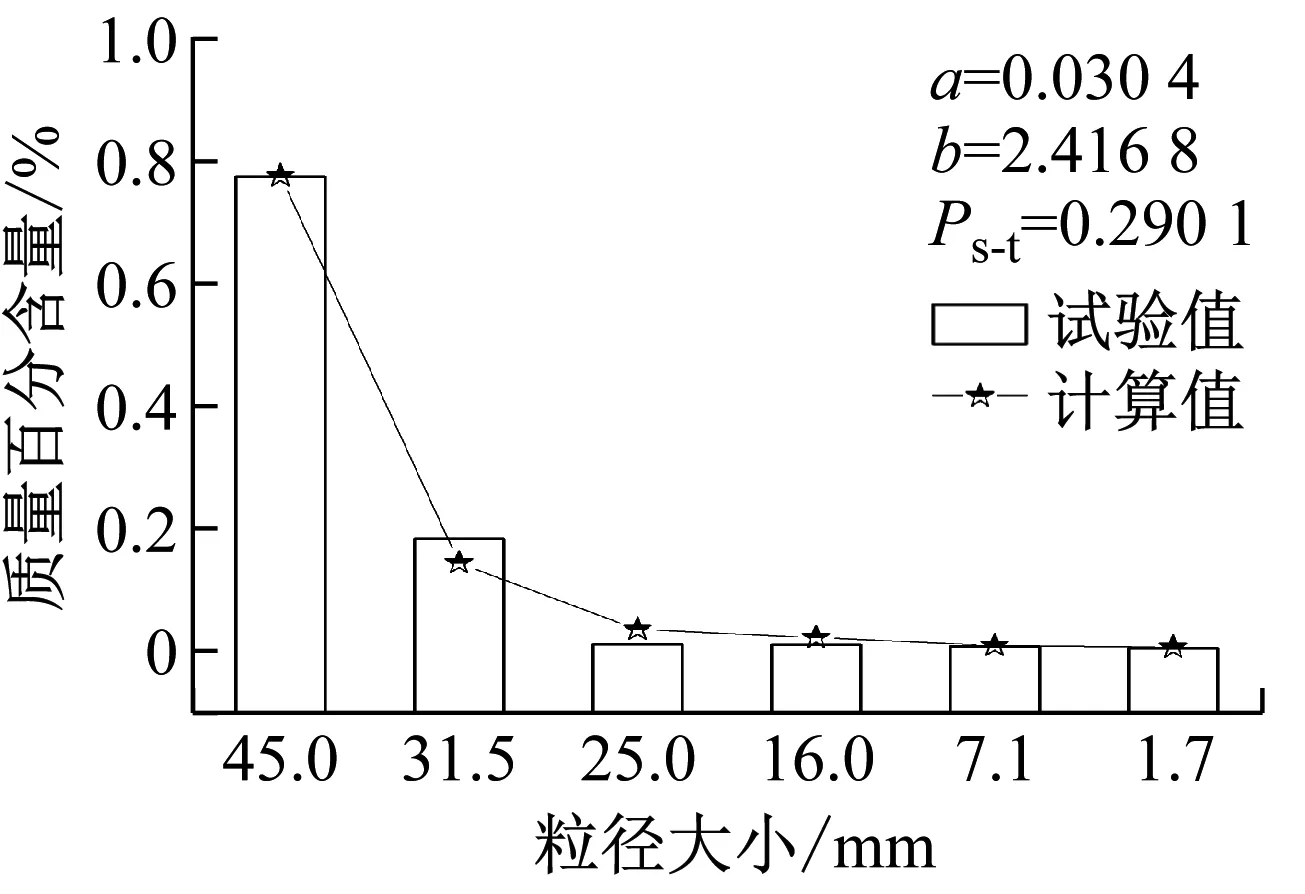
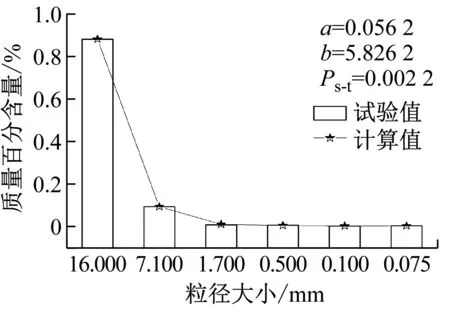
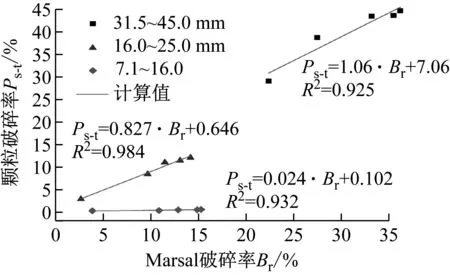
由文中动力破碎试验可知,颗粒破碎是一个由大粒径颗粒破碎为小粒径颗粒的不可逆过程,对于任意由单一粒径组Di(粒径范围为Di~Di-1)组成的材料,其将破碎到较小粒径组Dj(1≤j≤i-1)。定义小于Dj的颗粒累积质量占总破碎质量的百分数为F,即破碎百分率。同时,令粒径比xij=Dj/Di-1,则在xij与F的关系中,0 对动力破碎级配的变化进行分析,这里根据动力试验图7的数据,得到粒径比xij与破碎百分率F在坐标系中的关系,如图9所示。 (a) 粒径31.5~45.0 mm 从图9可知,粒径比xij与破碎百分率F可以用指数分布函数进行描述,如式(3) F=a·eb·xij (3) 式中:a与b为指数分布函数的参数;F为破碎百分率,%;xij为粒径比。对式(3)两边进行求导,可以得到指数分布函数的概率密度函数f,如式(4) f=F′=a·b·eb·xij (4) f的物理意义为该档粒径组破碎至较小粒径组的概率密度,粒径比xij的范围即为积分区间。从式(4)中可以看出,概率密度函数f根据a,b的不同而发生变化,a,b值对f曲线的影响如图10所示。 (a) 参数b为1时 从图10可知,a值和b值共同决定了概率密度函数f的峰值大小和曲线弯曲程度,但是当b值在小范围内变化时,曲线形态变化较大,因此b值的影响明显较a值要大。说明b值对颗粒破碎总量和各档粒径破碎分配比例的变化比较敏感,a值的敏感性相对较弱。 对式(3)两端取对数,得到式(5) ln(F)=lna+ln(eb·xij) (5) 即转化为式(6) ln(F)=lna+b·xij (6) 其中,令Y=ln(F),X=xij,c=lna,可得式(7) Y=c+bX (7) 由动力试验数据能够得到式(7)中的Y和X值,反演得到式(3)中的a和b值,最终确定描述动力破碎状态的指数函数式。 根据童晨曦等的研究,多粒径组破碎与单一粒径组不同,多粒径组颗粒破碎最显著的特点就是各粒径档的破碎概率很难确定,基本不可能得到各粒径的补偿量和破碎量。而实际情况中,很多时候只需弄清楚岩土材料总体破碎情况即可。多粒径组由有限个单一粒径组构成,单一粒径颗粒破碎形式符合指数分布函数的特点,因此多粒径组颗粒破碎可以看成是有限个指数分布函数的叠加,为了简化模型,根据动力试验结果可以假定不同粒径颗粒破碎符合相同的指数函数分布。 图11 颗粒破碎概率示意图 根据自然界岩土材料的特点,将颗粒材料的界限粒径分为i档,粒径从小到大为D1,D2,…,Di。同时,定义Markov链{Xn,n∈T},状态空间I={D1,D2,…,Di}。此外,条件概率Pij(n)=p{Xn+1=Dj|Xn=Di}为Markov链{Xn,n∈T}在时刻n的一步转移概率,且Dj,Di∈I。RT(0)=[r1(0),r2(0),…,ri(0)]为颗粒初始各级配百分含量向量,即初始概率向量;RT(n)=[r1(n),r2(n),…,ri(n)]为颗粒破碎后n时刻对应的各级配百分含量向量,即终止概率向量。根据破碎试验特征,颗粒破碎一般为试验一次后的破碎情况,即n=1。从上述可知,Markov链的一步转移概率矩阵,如式(8) (8) 式中,ηij为破碎概率系数,指粒径为Di粒径颗粒破碎到Dj粒径颗粒的量与Di粒径颗粒总破碎量的比值,如式(9) (9) 此外,由颗粒破碎矩阵可知 (10) 由式(3)可以得到 ηij=F(xij)-F(xij-1),xi0=0 (11) 初始概率向量和终止向量之间存在以下关系,如式(12) RT(n)=RT(0)P (12) 通过式(12)即可得到破碎后的各粒径质量百分含量。RT(0)和RT(n)分别为初始概率向量和终止概率向量,P为一步破碎概率矩阵。式中含有3个参量,即指数函数参数a,b和死亡概率Ps-t。a,b值可以通过式(7)得到,Ps-t可以通过最小二乘法得到。通过实际破碎后的终止概率向量与式(12)得到的计算终止概率向量之间无限逼近,采用最小二乘法构造以下目标函数,如式(13) (13) 对目标函数求导,即可求得相应的死亡概率Ps-t,代入式(12)即可得到破碎后各粒径质量百分数的计算值。 3.3.1 颗粒破碎模型有效性验证 为了验证所提出的Markov链破碎模型,采用文中动力三轴试验数据进行验证。参数a,b以及Ps-t如图12~图14所示。其中:a,b值由最终状态决定;Ps-t由初始状态和最终状态共同决定。 (a) 加载5 000次→10 000次 (a) 加载5 000次→10 000次 (a) 加载5 000次→10 000次 从图12~图14可知,本文提出的Markov链破碎模型能较好地描述不同粒径大小颗粒在动力作用下的颗粒破碎演化规律。对于原始粒径的减少以及次级粒径的增加都能进行较好的预测,充分证明了所提模型的有效性。该模型参数较少,只有3个参数,且容易从试验中获取,使得该模型能够较为简便的应用。为了进一步验证模型的有效性,采用文献[27]的碳酸盐砂环剪试验数据进行验证,如图15所示。 (a) 剪切应变9 040%→23 900% 从图15可知,该模型同样较好地描述了环剪试验的小粒径钙质砂的破碎演化过程,得到了多粒径组的不同初始状态和终止状态的级配变化过程。但是由于应力状态和岩性的不同,预测准确度相比动力试验还需提高。 从上述试验结果与计算值的对比可以得出,该破碎模型为多粒径组的破碎演化预测提供了一种可行的方法,适用于不同岩质的颗粒破碎材料的破碎演化预测。同时,该模型不仅可以描述破碎材料动力破碎状态,其他应力状态下的多粒径组破碎状态演化也可以进行描述。但是,由于颗粒破碎受多种因素的影响,模型针对不同岩性、应力状态等破碎材料的预测准确性有待提高,需要进一步研究。 3.3.2 Marsal破碎率Br与颗粒死亡率Ps-t的关系 此外,Marsal破碎率Br也是表征颗粒破碎的量化指标,其可以通过筛分试验直接得到,为了研究Marsal破碎率Br与颗粒死亡率Ps-t之间的关系,针对31.5~45.0 mm,16~25 mm和7.1~16.0 mm 3种粒径,以加载5 000次对应的质量百分数为初始状态,结合图8依次分析了不同动力加载次数后Br与Ps-t之间的关系,如图16所示。 图16 Marsal破碎率Br与死亡率Ps-t的关系 从图16可知,Marsal破碎率Br与死亡率Ps-t的关系可以用线性函数进行拟合,如式(14) Rs-t=A·Br+B (14) 式中:31.5~45.0 mm对应的A和B分别为1.06和 7.06;16~25 mm对应的A和B值分别为0.827和0.646;7.1~16.0 mm对应的A和B值分别为0.024和0.102,三者相关关系R2达到0.92以上。将式(14)代入式(8),即可得到关于Marsal破碎率Br的颗粒破碎模型。 本文采用动静三轴试验系统,针对红砂岩粗粒土进行了不同粒径大小和加载次数下的动力破碎试验,研究了红砂岩粗粒土的动力破碎现象和颗粒破碎演化规律,构建动力破碎概率密度函数,建立了颗粒破碎模型并进行了验证,模型预测有效性较好。得到以下结论: (1) 粒径组颗粒越大,动力变形值越大;7.5~16.0 mm和16~25 mm粒径加载至20 000次时,颗粒破碎达到稳定,而31.5~45.0 mm粒径加载至30 000次时,颗粒破碎达到稳定,小粒径组比大粒径组土体颗粒破碎完成较早,土体结构易于趋于稳定。 (2) 粗粒土软化系数与加载次数的关系与黏土的不同,粗粒土呈半对数关系,而黏土呈线性关系。粒径组颗粒越大,软化系数越小。 (3) 动力作用下粗粒土破碎率存在一个极限值,颗粒组存在一个极限级配。大粒径颗粒破碎后主要演化呈下一档粒径颗粒和细小粒径颗粒,其余粒径组颗粒分配量较少。 (4) 建立的颗粒破碎模型能对不同应力状态下的多粒径粗粒土破碎演化进行描述,但是由于破碎影响因素的多样性,对于不同岩性和应力状态下的颗粒破碎预测准确性还需进一步提高。 (5) 构建了常用破碎指标Marsal破碎率Br与颗粒死亡率Ps-t之间的关系,两者呈线性关系,相关关系R2达到0.92以上。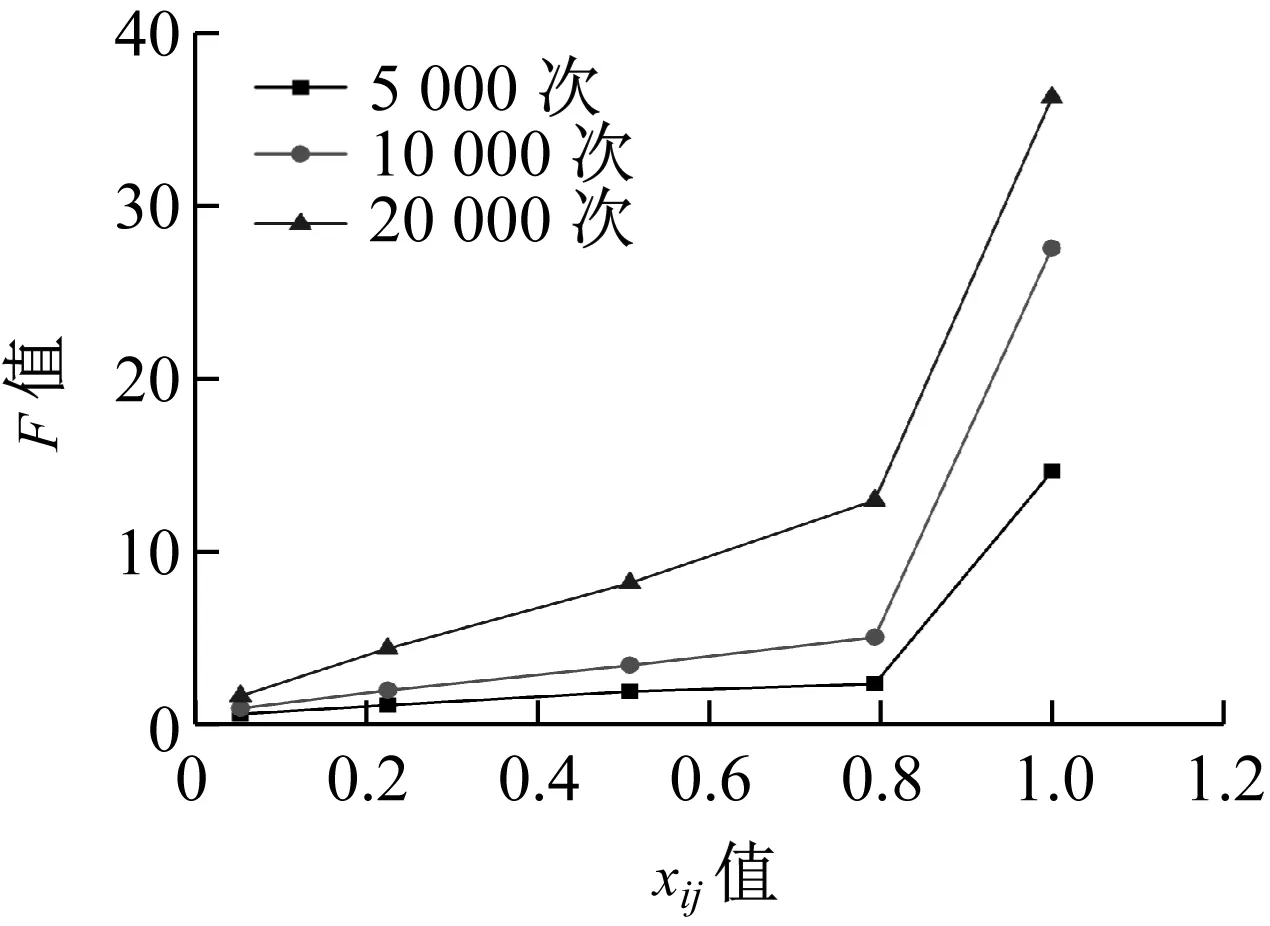

3.2 多粒径组破碎模型

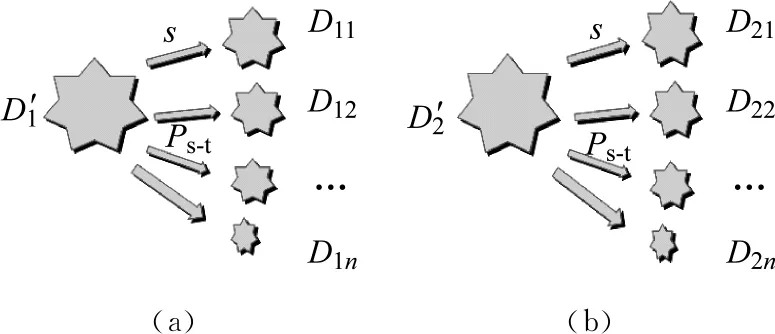
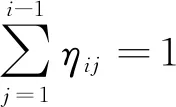
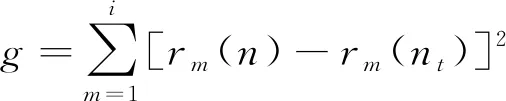
3.3 颗粒破碎模型验证


4 结 论
