颗粒自激式冲击-振动耦合力学试验方法及试验研究

李飞胤， 马少杰， 张 合

(南京理工大学 机械工程学院，南京 210094)

生产生活中的许多核心零部件工作在连续冲击-振动耦合力学作用环境下，典型如冲击钻活塞部件、发动机气门结构、矿山减速机和采煤机核心部件等；此外，军事应用中的拦截导弹机动变轨飞行时，其姿轨控制发动机间歇点火横向脉冲冲击与飞行器自身振动同样在弹体结构上产生冲击-振动耦合环境[1]；侵彻弹药高速侵彻多层硬目标结构过程中，其引信机构及控制组件等不但直接承受穿层过程的连续高冲击过载，且由于结构响应振动及冲击应力波的加载与传递，也使得弹体结构上耦合了大量的振动响应，其力学环境同样呈现冲击-振动耦合作用特征[2-3]。科学技术人员早已认识到耦合力学环境会对系统及结构间相互作用产生额外影响，在耦合条件下不同力学环境因素之间往往具有极为复杂的交联关系，且各独立参数之间也存在不同程度的非线性化现象[4-5]，因此，对于此类产品及结构的考核测试，单一力学作用分离考核可能无法有效分析故障问题的根本规律和本质机理，耦合力学环境作用下的产品及结构件等应采用耦合力学试验手段进行测试验证[6]。

现有的连续冲击力学考核测试中，常用空气炮、马歇特锤等单次冲击手段重复加载实现，不但连续冲击频率难以控制，且冲击幅值也存在较大散布；此外，对于本文研究中所需的耦合振动加载，已有的气动、液压、偏心连杆等振动加载方式激振频率有限，而电磁振动虽可实现较高的加载频率，但振动加速度幅值通常较为有限，且其动圈结构也难以承受高冲击载荷作用，与冲击加载作用之间存在固有矛盾。由上述分析可知，不但现有的各类连续冲击、振动加载方法难以满足高动态测试需求，并更是缺乏一种有效的连续冲击-振动耦合力学试验技术，可实现苛刻环境下结构件的耦合力学作用等效考核，迫切的应用需求使得亟需开展新体制力学试验技术研究。

本文针对冲击-振动耦合力学试验需求，设计了基于旋转式连续冲击加载及颗粒体自激振动加载的耦合力学试验系统。为有效实现所需的耦合振动响应，根据本文系统动力学特征，基于EDEM软件和VC++二次开发建立了离散元耦合仿真模型，通过仿真结果确定了自激振动结构的优化选择方案，在此基础上开展试验研究，验证力学试验系统的实际工作性能。

1 冲击-振动耦合力学试验系统设计

设计的冲击-振动耦合力学试验系统方案，如图1所示。试验系统主体为大质量的高强度转台，等间隔安装有多组冲击组件，通过电机带动转台旋转实现对被冲击件的冲击加载，冲击组件具有阻尼转轴结构，冲击发生后可绕轴旋转快速退让，并在转台旋转离心力的作用下快速复位，有效突破了现有连续冲击试验体制冲击频率的限制。

图1 力学试验系统方案

匹配转台旋转式冲击方案设计的自激振动加载机构，如图2所示。主要由立方体基座及其端盖，试件夹具，可拆卸颗粒体腔，重荷弹簧，振动杆，压帽和复位弹簧等部分组成。立方体基座及其端盖提供被冲击部分的结构限位和支撑，试件夹具用于安装测试对象并直接承受冲击组件的连续冲击载荷作用，夹具底部设计有可拆卸的颗粒体腔，通过置入颗粒体的方式，在激励作用下产生复杂的受激碰撞作用，形成多频自激振动加载，振动杆与外部主动激振装置连接，通过主动激振加载进一步增加被冲击结构上的振动响应，重荷弹簧为冲击加载和主动激振相互作用提供柔性连接，其受激振荡运动也可进一步增加颗粒体的振动响应，形成频率更丰富的多频振动加载；压帽和复位弹簧共同为振动杆提供结构复位。

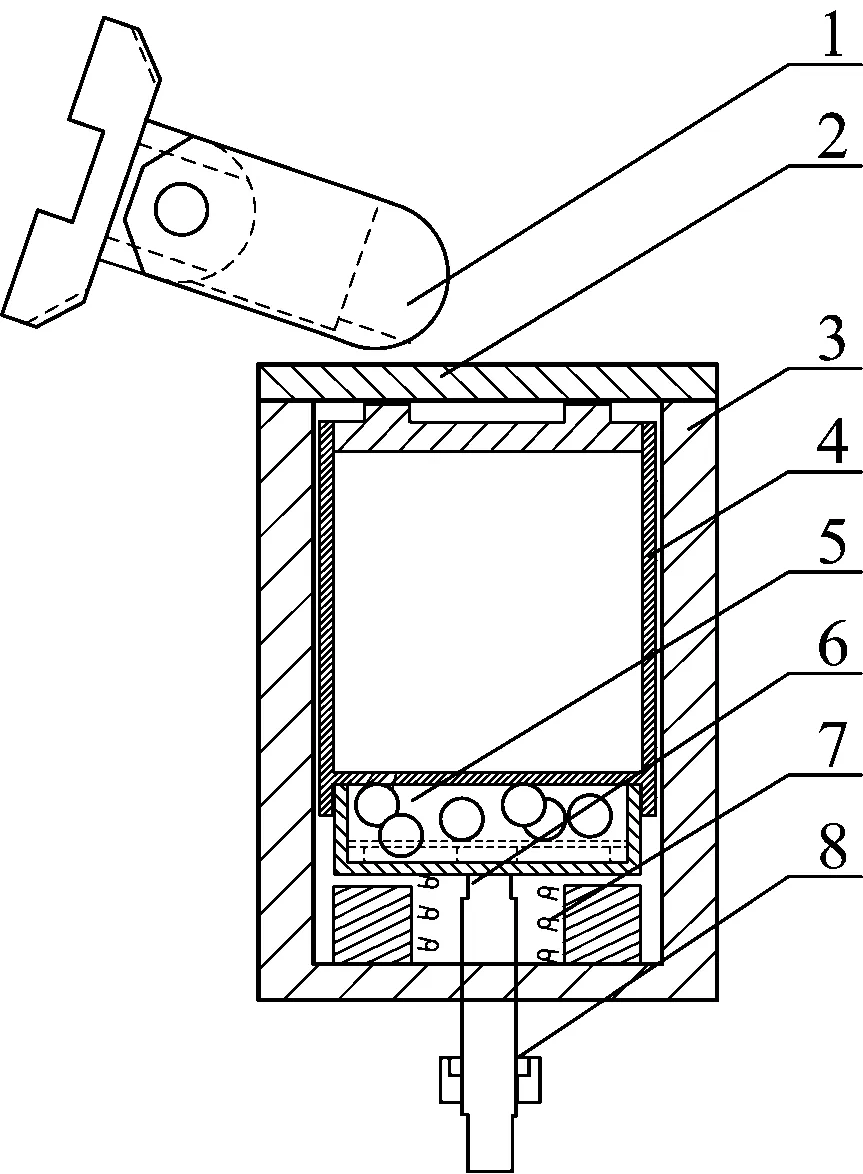
1.冲击头;2.端盖;3.立方体基座;4.试件夹具;5.可拆卸颗粒体腔;6.振动杆;7.重荷弹簧;8.压帽和复位弹簧。

2 力学试验系统离散元耦合仿真建模

2.1 离散元方法基础模型

对于所研究的冲击-振动耦合力学试验系统，冲击组件与主动激振的力学作用及动力学响应通常较为直观清晰，而对于本文重点关注的颗粒体多频自激振动加载，其作用效果依赖于离散元系统在激励加载下的动力学响应，根据第1章的分析，该部分振动分量源自于自激振动结构中颗粒体间以及颗粒体与结构间的复杂碰撞接触作用，对于此类动力学问题，有限元分析方法计算耗费极高，求解较慢，多体动力学分析方法建模复杂，且对不同条件情形进行分析时更需重新建模，工作量繁重。离散元方法则是面向于非连续介质力学的有效数值分析方法，充分避免了对离散单元的网格划分等，直接通过分离结构间的力学方程进行求解计算，具有较好的分析精度和计算效率，因此被广泛应用于各类离散单元系统动力学问题的分析[7-9]，对于本文中的应用情形同样具有较好效果。

离散元方法的基本原理是将分析系统视为离散单元的结合，以时间步长为单位，计算步长时间内离散单元间以及离散单元与结构间的接触作用力，基于牛顿定律建立并求解每个离散单元的运动方程，以此更新离散单元的运动状态和空间位置等，并在此基础上进行迭代计算，获得系统完整时间历程的动力学响应。由过程原理可知，离散元方法中涉及到的分析建模方法主要包含两部分，分别为离散单元的接触问题和动力学问题，根据离散元方法基础理论，通常定义如下的接触力方程描述离散单元之间以及离散单元与结构之间的相互接触作用[10-11]

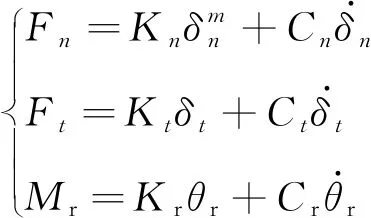
(1)

当切向接触力或转动力矩大于接触部位最大静摩擦力时，离散单元之间将产生滑动，此时切向接触力或转动力矩等应按摩擦力进行修正，即有[12]

(2)

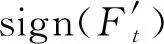
根据上述离散单元接触模型，则可基于牛顿定律建立如下的参考单元运动方程

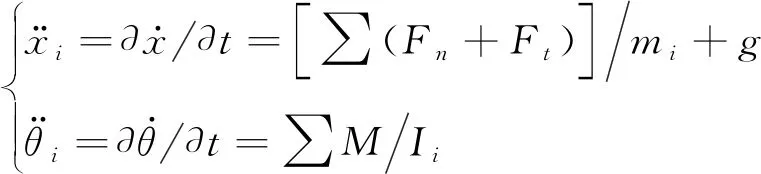
(3)

由中心差分法可得半时间步长的离散单元运动方程

(4)

将式(3)代入式(4)可得

(5)

对式(5)进行积分可得位移方程

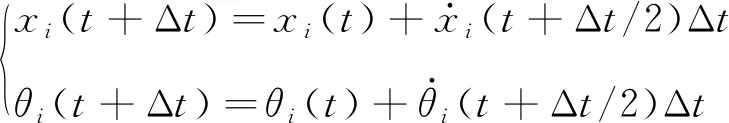
(6)

将该位移方程代入接触模型中，如此循环计算，即可实现离散元系统动力学问题的分析求解。

2.2 离散元-动力学耦合仿真建模

在一般的离散元问题分析建模中，通常仅能够为结构或离散单元添加简单的动力学参数，不符合本文力学试验系统在冲击及激振加载下结构运动所产生的颗粒体复杂自激振动响应特征，因此，为有效获得符合本文应用情形的动力学仿真条件，研究中进一步分析并建立离散元-动力学耦合仿真。对于本文的力学试验系统，转台驱动多组冲击组件的连续冲击加载和振动杆的激振加载是颗粒体产生自激振动的主要激励，因此，耦合仿真中通过自定义函数导入上述激励参数，作为颗粒体的动力学输入。结合离散元软件的二次开发，得到颗粒体在上述激励下动力学响应的一般规律，为自激振动方案的选择提供研究支撑。

根据给出的离散元方法基本原理，基于VC++二次开发力学试验系统的离散元-动力学耦合仿真程序，耦合程序块如图3所示，该程序主要流程结构如下：① 声明耦合编程所需的函数库及头文件等；② 定义结构体类，声明其属性变量；③ 配置仿真时长、步长、数据交换率等，并给定几何体参数；④ 建立C程序与EDEM耦合仿真接口间的连接；⑤ 仿真主循环，以步长时间为单位，获取颗粒体对结构体的作用力，结合导入的冲击及激振作用力数据，求解结构体的运动参数，并传递至EDEM中完成结构体的动力学参数更新；通过该过程的循环计算实现整个时间历程动力学问题的求解。主要耦合计算流程，如图4所示。

图3 耦合计算程序块

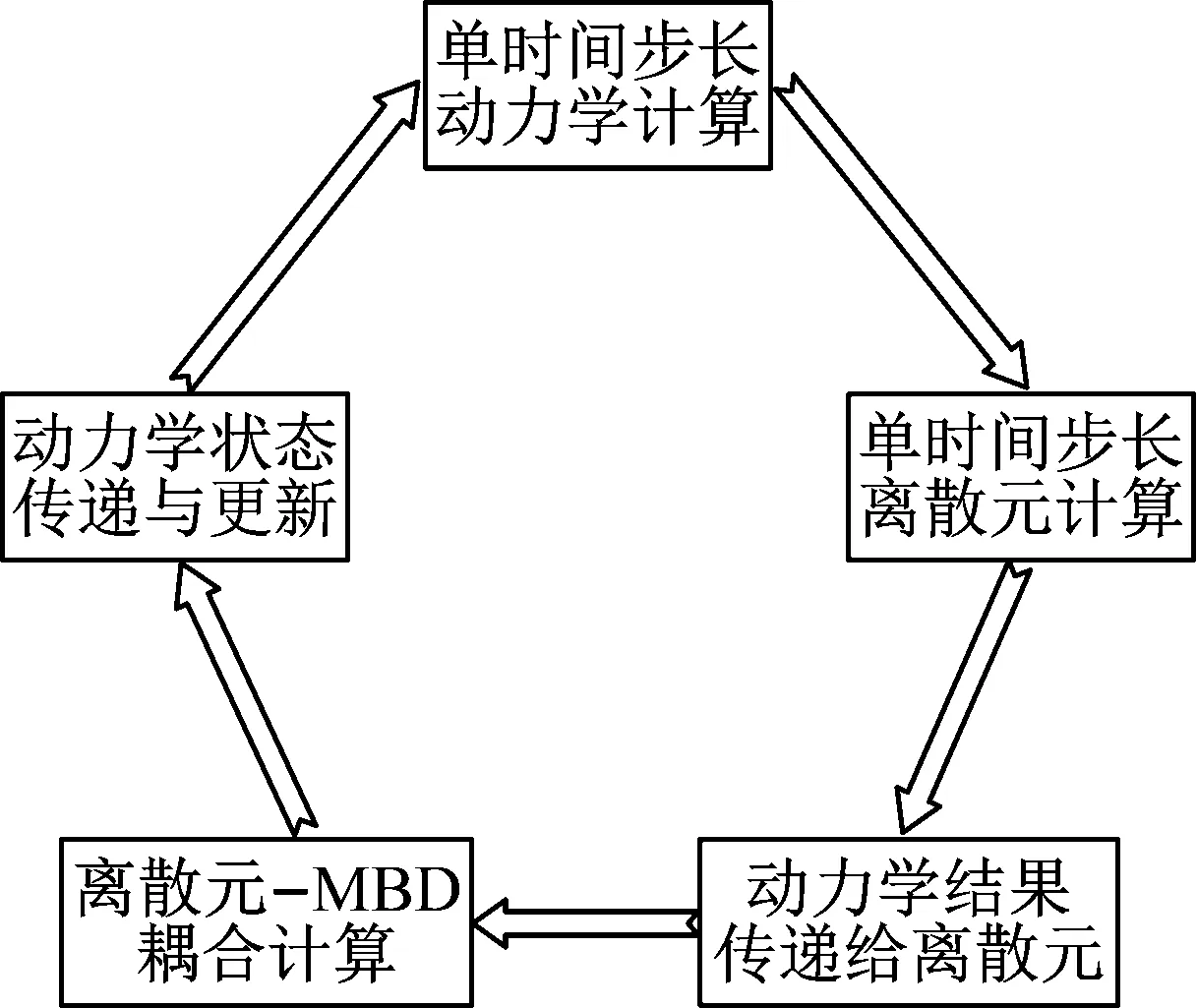
图4 耦合计算流程

提取自激振动加载结构三维模型，在EDEM软件中建立离散元仿真模型，如图5所示。建模中对原模型的螺纹连接结构进行合并简化，并以颗粒体腔作为离散元仿真的颗粒体生成单元，根据设计参数配置模型几何材料为45钢，并给整个仿真域添加重力加速度-9.8 m/s2，颗粒体参数则根据仿真条件给出。

图5 离散元建模

3 动力学响应仿真分析

基于建立的离散元-动力学耦合仿真模型，分析不同条件下的颗粒体自激振动响应规律。

3.1 颗粒材质

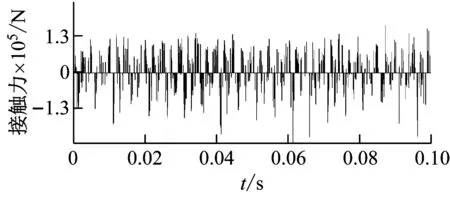
分别选择3种不同密度的颗粒体材料进行仿真分析，材料特性参数如表1所示，统一给定颗粒体粒径为10 mm，数量为12。仿真获得的颗粒体对结构整体的冲击力时域波形如图6所示。

(a) Al

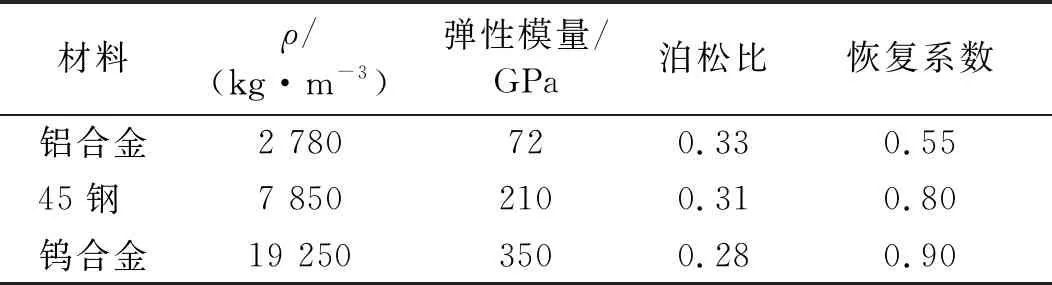
表1 颗粒体材料及属性

从仿真结果可以看出，本文提出的颗粒体自激振动加载方案在结构上产生了多频振动加载效果，在冲击幅值方面，随着材料密度的增大，颗粒体质量增加，因此获得的自激振动冲击力也随之增加；此外，从曲线的时域特征还可进一步看出，不同材质颗粒体获得的等效自激振动加载频率也并不相同，该现象的出现与材料的弹性模量和碰撞恢复系数有关，弹性模量和碰撞恢复系数越大，获得的自激振动频率响应特征也越复杂；总体来看，颗粒体材质差异最主要影响获得的冲击力幅值，实际应用中，可根据所需的振动幅值参数，对颗粒体材料进行选配。

3.2 颗粒数量

选择颗粒体材质为45钢，并给定颗粒体粒径为10 mm，分析颗粒体数量分别为6，12，18和24等4组条件下颗粒体对结构整体的冲击力时域波形，如图7所示。

(a) n=6

从仿真结果可以看出：相同材质和粒径情形下，不同数量颗粒体获得的自激振动冲击力幅值范围基本较为一致；在响应频率方面，当颗粒体数量较少时，随着颗粒体数量的增加，等效冲击频率增加，但当颗粒体数量超过一定数值时，自激振动响应频率随着颗粒体数量的增加出现下降趋势，这是由于在有限的自激振动结构空间内，随着颗粒体数量的增多，颗粒体的有效行程空间减小，造成颗粒体对结构的碰撞作用下降，等效降低了自激振动的响应频率。

3.3 颗粒粒径

选择颗粒体材质为45钢，数量为12，分析颗粒体粒径分别为5 mm，10 mm，15 mm和20 mm等4组条件下颗粒体对结构体的冲击力时域波形及其频率分布，如图8所示。

(a) 5 mm

从仿真结果可以看出:自激振动冲击力幅值基本随粒径增加而增大，但其增幅相比较于材料变化较为有限；自激振动响应频率随着粒径的增加而增加，超过一定数值后，则随着颗粒体粒径的增加而减小，这是由于在颗粒体数量一定的情形下，粒径较小时颗粒体的质量较轻，体积占比也较小，因而在腔体结构内的分布较为稀疏，使得颗粒体间动能交换的概率较小；随着颗粒体粒径的增加，质量相应增加，体积占比也随之增加，从而增加了相互间碰撞作用概率，使得自激振动冲击力幅值和响应频率增加；而当颗粒体粒径超过一定数值后，颗粒体在结构腔内的行程空间极为有限，且力链方向也逐渐集中归一，使得等效自激振动响应频率降低。

3.4 混合粒径

选择颗粒体材质为45钢，数量为12，分析颗粒体粒径分别为10 mm-15 mm组合、15 mm-20 mm组合以及10 mm-15 mm-20 mm组合等3组条件下颗粒体对结构体的冲击力时域波形及其频率分布，如图9所示。

(a) 10 mm-15 mm

从仿真结果可以看出:自激振动冲击力幅值随着颗粒体总体粒径量级的增加而增加，这是由于自激振动冲击力幅值主要与颗粒体质量相关，因此最大粒径颗粒体决定了等效冲击力的峰值；自激振动响应频率则先随着粒径的增加而增加，超过一定数值后，则会随着粒径的增加而减小；并且，对比单一粒径仿真结果，相同情形下混合粒径时的自激振动冲击力幅值和响应频率相对较低，这是由于颗粒体粒径相互补情况下，受激运动过程中更多能量交换发生在颗粒体系统内部，导致颗粒体对结构的碰撞作用效果相对较弱，使得等效自激振动冲击力频率下降。

基于上述仿真结果，配置颗粒体自激振动加载方案。根据力学试验系统应用需求，在自激振动冲击幅值方面，选择45钢材料颗粒体即可满足需求，而响应频率方面，尽量在有限空间颗粒体腔情形下获得更为丰富的振动频率，因此，选择单一粒径颗粒体方案，粒径为15 mm，数量为18，可获得最为理想的自激振动效果。

4 仿真及试验验证

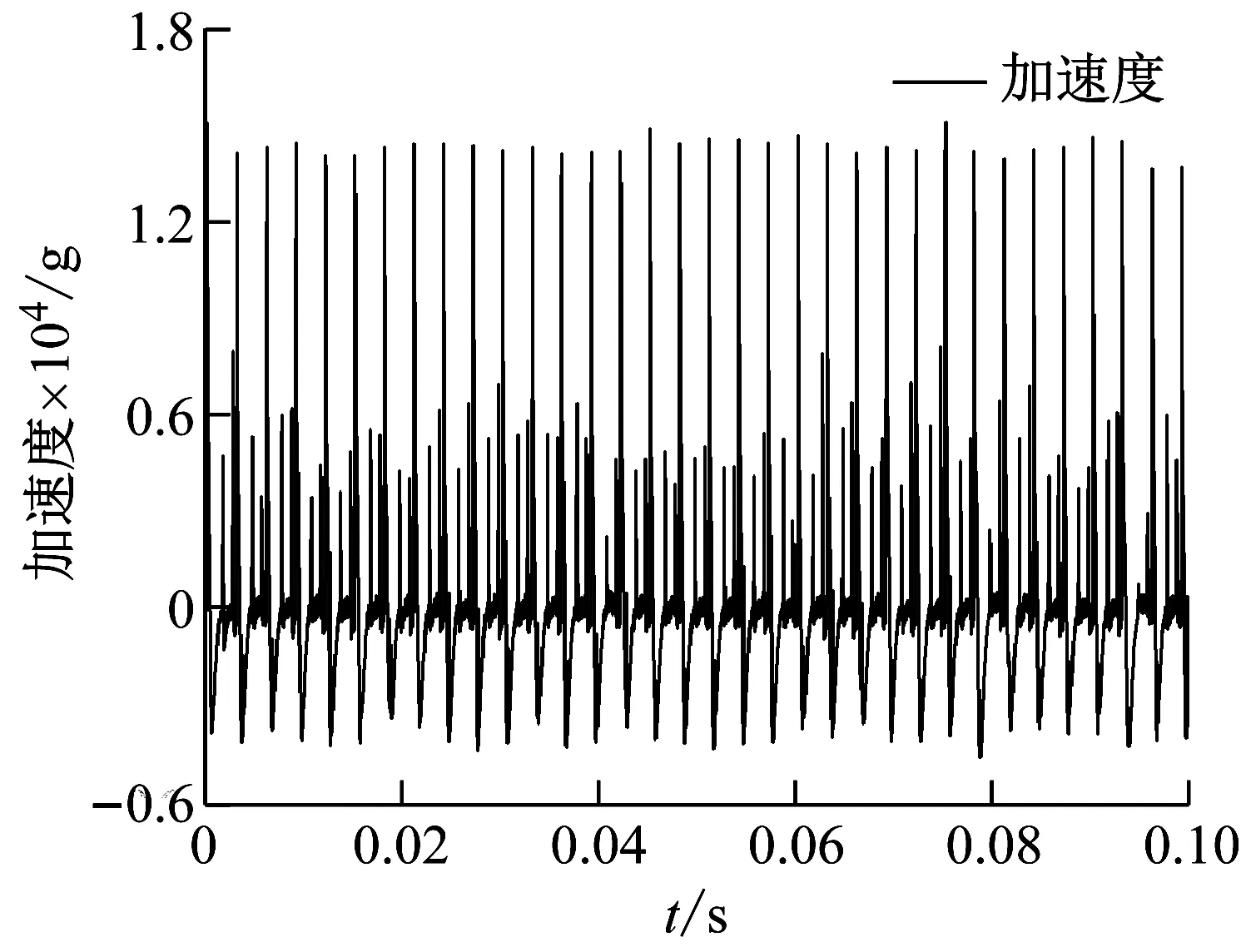
根据第1章的分析，力学试验系统受冲击头连续冲击、振动杆主动激振以及颗粒体自激振动的复合加载作用。为进一步分析对比系统响应，研究并建立系统整体的动力学仿真。根据典型应用条件，仿真中配置冲击加载间隔3 ms，振动杆主动激振加载间隔5 ms，分别对不加载颗粒体单元和加载颗粒体单元两种情况进行对比分析，仿真结果如图10所示。

(a) 连续冲击-主动激振加载响应加速度

图10(a)为连续冲击-主动激振加载作用下被冲击件的响应加速度，图10(a)可明显看出该响应加速度主要由两部分组成，其中连续冲击加速度主要在13 000g左右，幅值变化较小；主动激振加速度通常在3 000～8 000g，幅值变化较大，与高冲击加载引起的被冲击件运动位置、速度等不一致，导致的冲击状态变化有关；但总体来看，不加载颗粒体单元情形下，被冲击件上获得的响应加速度较为单一，未能产生理想的冲击-振动耦合力学响应特征。图10(b)为加载了颗粒体单元后被冲击上获得的响应加速度，从图10(b)可以看出，原本较为规律的响应加速度中叠加了大量极为复杂的扰动分量，该扰动分量的幅值和频率均无明显规律，且与主动激振加载的响应加速度发生了混叠粘连，并进一步影响到了冲击加速度正负形幅值的一致性，体现出复合了颗粒体自激振动加载后，系统动力学响应的复杂性。

在此基础上开展试验研究，试验方案设计如图11(a)所示;完成试验件安装的系统平台如图11(b)所示。

(a) 自激振动方案设计

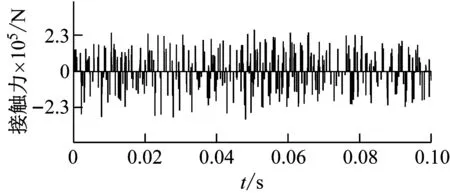
分别开展无颗粒体的连续冲击加载试验和置入颗粒体的冲击-振动耦合加载试验进行对比验证，通过转台转速闭环控制稳定连续冲击加载间隔3 ms，采用加速度传感器采集被冲击结构的响应，试验结果如图12所示。

图12(a)为连续冲击加载下被冲击结构的响应加速度波形，图中的6组加速度脉冲对应于连续6次冲击加载过程，从图12(a)可以看出:该加速度波形轮廓特征清晰，每组加速度脉冲由碰撞接触所形成的峰值加速度和衰减的结构响应振荡加速度所构成，不同组加速度脉冲之间辨识特征清晰，无交联耦合现象；试验获得的主要冲击加速度幅值在11 000g左右，间隔3 ms，不同组冲击加速度峰值存在一定波动，这是由于连续冲击试验中，被冲击结构在高动态加载作用下，存在较为复杂的动态运动响应，由此引起连续冲击作用时接触对的相对速度大小、方向、接触部位等不一致所导致的。

(a) 连续冲击响应加速度

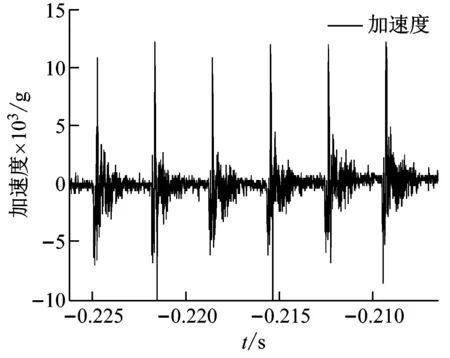
图12(b)为配置了颗粒体自激振动加载后得到被冲击结构响应加速度波形，结合试验时相同的冲击加载条件和加速度响应的时域聚集特征可一定程度上分辨出连续6次冲击作用过程，但从图12(b)可以明显看出:置入颗粒体后的冲击-振动耦合作用下，主要响应加速度幅值增加至13 000g左右，间隔3 ms，加速度峰值的波动也更为剧烈，并产生了若干极高幅值的扰动分量；从时域过程上看，不但每次冲击作用时刻附近产生了极为复杂的响应加速度，且相邻冲击间隔过程中也存在大量的响应加速度脉冲，加速度时域信号出现粘连现象。

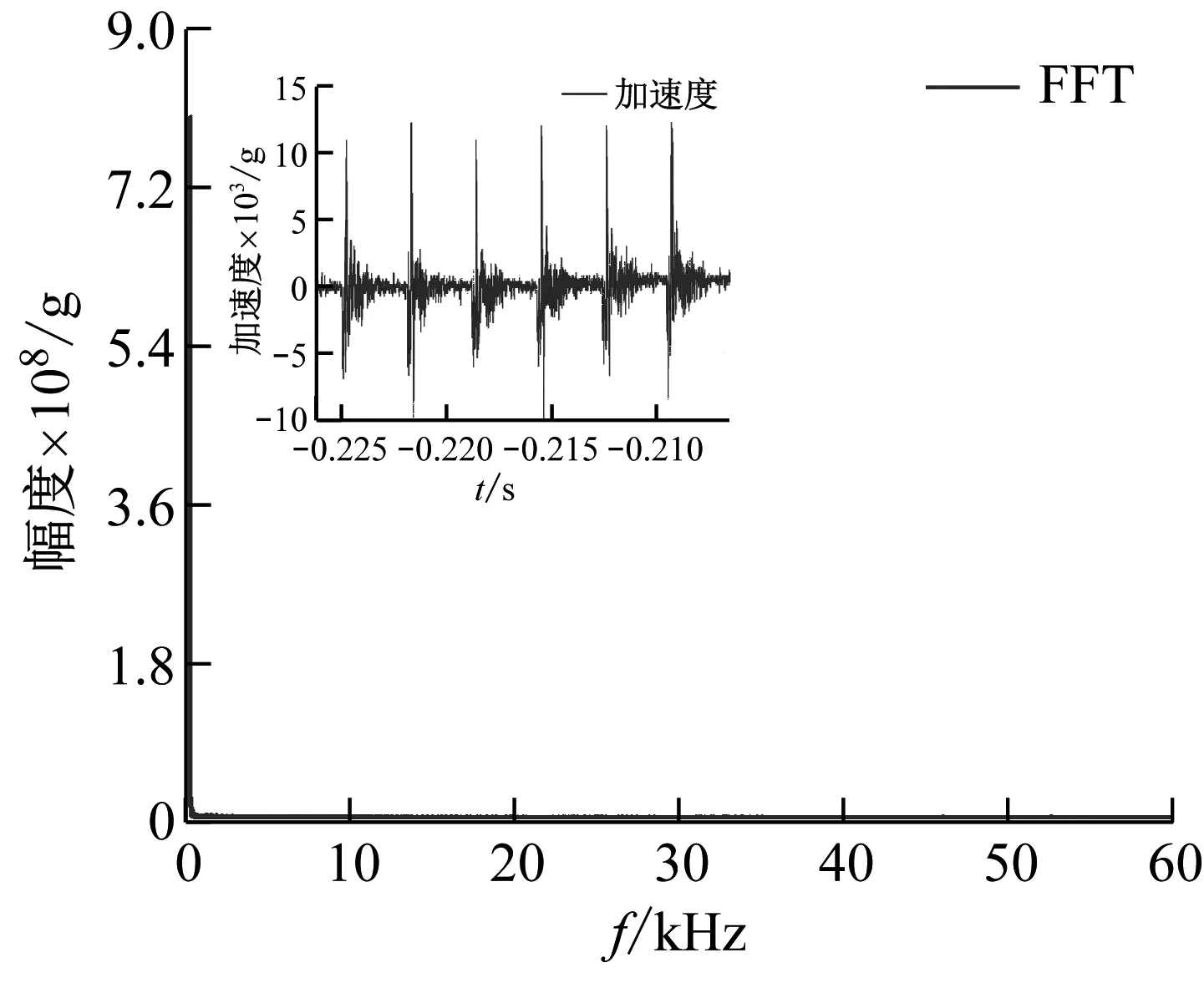
对于本文中连续冲击与冲击-振动耦合两种加载方式的对比分析，重点关注的是加速度响应中频率组成差异。分别提取图12中的连续冲击响应加速度和冲击-振动耦合响应加速度，进行快速傅里叶变换，获得加速度信号的幅度谱特征如图13所示。对比图13(a)和图13(b)可以看出，连续冲击试验响应加速度的频率成分较为单一，主要集中在基频段，且仅在临近基频的低频段存在少量频率分布，而置入颗粒体的冲击-振动耦合试验中，响应加速度则具有极为复杂的频率分布，涵盖了从低频至高频的宽频带范围，且幅度特征也极为复杂，无明显规律性，该对比分析结果更进一步验证了，在设计的连续冲击加载方案基础上，结合仿真结果配置的颗粒体自激振动加载方案，可获得频率丰富的响应加速度，验证了本文所设计的颗粒体自激振动加载方案的有效性。

(a) 连续冲击加速度频域分析

5 结 论

本文针对现有冲击-振动耦合力学试验手段的不足，提出了一种连续冲击与多频振动耦合的力学试验方法，设计了试验系统样机，通过转台驱动旋转自退让冲击组件实现连续高幅值冲击加载，通过主动激振加载和颗粒体自激振动实现复杂多频振动耦合加载，可满足苛刻环境下的冲击-振动耦合试验需求。

(1) 根据试验系统的工作原理和结构参数，基于EDEM和VC++二次开发建立了适用于本系统的离散元-动力学耦合仿真模型，获得了颗粒体自激振动响应规律，并根据仿真结果和应用需求，配置了颗粒体自激振动加载方案。

(2) 基于设计的试验系统样机和配置的颗粒体自激振动加载方案，开展试验研究，在连续冲击试验中获得了主要幅值11 000g，间隔3 ms，时域轮廓清晰，波形峰值波动较为平缓的响应加速度；在冲击-振动耦合试验中获得了主要幅值13 000g，间隔3 ms，时域信号粘连，波形峰值波动剧烈的响应加速度。

(3) 结合频域分析结果进一步得出，连续冲击试验主要频率成分集中在基频附近，并仅在临近基频的较窄频段范围存在有一定的频率分布；而冲击-振动耦合试验则具有极为复杂的频率分布，不但频率范围覆盖低频至高频的全部频段，且分布特征复杂，无明显规律性。

通过上述对比试验及结果分析可知，本文所设计的力学试验系统和配置的颗粒体自激振动加载方案，可实现典型连续冲击和冲击-振动耦合等力学作用环境的等效模拟，该试验系统不但可用于一些关键零部件或材料的性能测试，还可根据测试需求，配置不同的颗粒体自激振动加载方案，模拟高速多层侵彻过程的加速度信号粘连力学环境特征，实现对侵彻弹药结构强度和计层起爆控制策略的实验室等效验证，研究具有较好的科学意义。