利用声信号基于HHT方法识别螺旋桨模态参数

刘正浩， 丁 举， 毛献群

(1. 中国船舶及海洋工程设计研究院， 上海 200011； 2. 喷水推进技术重点实验室， 上海 200011)

随着对螺旋桨静音性能的要求愈加严格，在设计中对螺旋桨的动力响应特性更加重视[1-2]。螺旋桨的模态参数是进行动力响应分析的前提和基础[3]，在这方面，黄政等[4-7]开展了螺旋桨模态的数值与试验研究，这些研究中，分别是通过加速度传感器和电阻应变片对桨叶动态响应进行测量，得到固有频率和模态阻尼比等参数。吴武辉等还进一步研究了传感器质量效应对于频率测量结果的影响，说明随着传感器数量增加，试验得到的固有频率有明显的降低。实际上，螺旋桨模态试验常常针对缩尺模型展开，对于缩尺桨模，单桨叶和传感器的质量对比并未达到可忽略传感器质量效应的程度，并且，高阶模态由于模态有效质量更小，对于传感器的质量效应更加敏感，试验结果可能带有更大误差。由于接触式测量方法用于螺旋桨模态试验的弊端，本文研究了利用声信号并基于希尔伯特-黄变换(Hilbert-Huang transform，HHT)方法识别螺旋桨的模态参数。HHT包含经验模式分解和希尔伯特变换两步，是一种处理非线性、非平稳信号的方法[8-9]。目前，该方法在水利和建筑等行业有应用的先例。范兴超等[10]使用该方法针对飞机模型的加速度响应信号进行了模态参数的识别；针对位移响应信号，魏博文等[11]基于HHT识别拱坝的固有频率和阻尼比。在利用声信号并基于HHT方法识别结构模态参数方面，夏茂龙等[12]研究了利用近场声信号并基于HHT方法识别结构模态参数，并通过数值算例说明了该方法的准确性。本文基于声学外场边界元理论，推导了结构物在冲击作用下的声辐射信号与模态参数的数学模型，突破了进行模态参数识别必须采用近场声信号的限制，并通过数值模拟进行验证，证明了所建立数学模型的准确性，同时还验证了该方法在较低的信噪比(signal-noise ratio，SNR)下仍具有足够高的识别精度。在此基础上，本文将该方法应用到螺旋桨模型的模态参数识别试验中，成功通过该方法识别得到螺旋桨模型的前两阶模态频率和阻尼比，明确该方法在实际工程中实用、有效。

1 理 论

1.1 结构振动声信号与模态参数的关系

自由空间中，结构物振动声辐射的过程可通过基尔霍夫-赫姆霍兹方程进行描述[13]，如式(1)是无空间分布声源的情况，空间中一点的声压PF(r,t)可通过振动结构表面的声压和速度分布积分得到

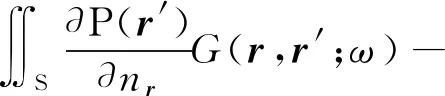
(1)

式中：r′为位移矢量；nr′为结构表面法向；S为结构物表面；P(r′)为结构表面的声压分布；G(r,r′;ω)=exp(ik·|r-r′|)/4π|r-r′|为三维空间格林函数。对式(1)，通过边界元方法，可表示成矩阵方程的形式，首先将场点布置于结构物表面，并作边界元离散，得到矩阵方程式如下

(2)

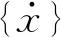
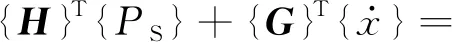
(3)

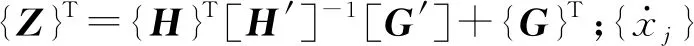
(4)

结构物的振型方程可以采用有限元形式表示如下

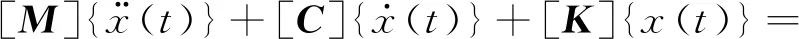
{F(t)}

(5)

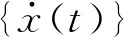
{x(t)}=[Φ]{q(t)}

(6)

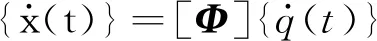
(7)

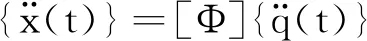
(8)

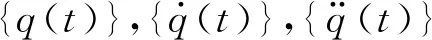
[Mr]-1[Φ]T{F(t)}

(9)

式中：[Cr]=[Mr]-1[Φ]T[C][Φ]，其中[C]为阻尼矩阵；[Kr]=[Mr]-1[Φ]T[K][Φ]，[K]为刚度矩阵；[Mr]=[Φ]T[M][Φ]，[M]为质量矩阵，这些都是对角矩阵。矩阵方程式(9)中，第j阶模态节点的振动方程可为

(10)

式中，{F(t)}为作用于结构物表面作用力向量，假设在k节点作用一个冲击载荷fk(t)=δ(t)并且其他节点上没有作用力，则式(10)可表示成

(11)

式中:ωj为第j阶固有频率；ζj为第j阶模态的阻尼比；φjk为j阶振型向量的第k个元素。

对于式(11)，可求解得到

(12)

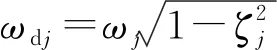
由式(7)有

(13)

其中，第p个节点的速度响应可以表示为

(14)

其中

(15)

表示第j阶模态振型对于节点p速度响应的贡献。φpj,k为j阶振型中节点p和k的相位差，Bpj,k=φpj/mωdj。将式(15)代入式(4)，则由于结构物第j阶模态响应引起的空间中场点F的声压可以表示成

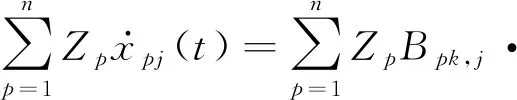
(16)

式(16)建立了场点F的声信号与结构物模态参数之间的关系。

1.2 HHT方法识别模态参数

1.2.1 经验模态分解方法

经验模态分解方法(empirical mode decomposition, EMD)认为任何复杂的信号都是由一些不同尺度的本征模态函数(intrinsic mode function, IMF)构成。每个IMF具有以下特征：极点和零点的数量相等或者相差一个，极点之间形成的上下包络线的平均值始终为零。由于具有这样的性质，IMF具有良好的希尔伯特变换特性。其分解过程表达如下

(17)

式中：P(t)为原始信号；Pj(t)为从原始信号分解出来的m阶IMF；r(t)为原始信号中的常量。对于式(3)所表示的声信号，经EMD分解之后的每一个IMF并不和每一阶模态响应一一对应。文献[14]证明，先以某一阶模态频率为中心频率对原始信号进行带通滤波，再进行EMD，得到的第一阶IMF就是结构的对应阶模态响应数据。在带通滤波处理上，文献[15]和夏茂龙等的研究采用Chebyshev I 类带通滤波器，本文工作中经过实践，从减小滤波信号相位延迟考虑，采用有限脉冲响应(finite impulse response，FIR)线性滤波器。

1.2.2 模态参数识别

对采样得到的声压进行希尔伯特变换及化简过程可参考Huang等的研究和文献[16]。最后得到声压解析信号的瞬时幅值和瞬时相位如下

(18)

(19)

对于式(18)等号两边取对数，得到

(20)

即瞬时幅值的对数和时间之间存在线性关系，斜率就是-ζjωj。并且从式(19)可见瞬时相位和时间成线性关系，斜率是ωdj。假设

-ζjωj=k1

(21)

ωdj=k2

(22)

斜率k1和k2可通过线性拟合得到，联立

(23)

就可以计算得到第j阶模态的固有频率ωj和阻尼比ζj。

经以上分析，利用结构物的冲击声辐射信号并基于HHT方法进行模态参数识别的流程总结如图1所示。

图1 模态参数识别流程图

2 数值模拟

在本章，通过数值模拟首先对目标桨模进行模态分析，得到桨模的前两阶固有频率，在此基础上，分别基于瞬态振动分析方法和瞬态声学边界元方法进行桨模在冲击载荷作用下的振动响应和声辐射仿真，最后提取一段时间的声信号进行HHT分析，从而从数值仿真的角度评估HHT方法识别螺旋桨模态参数的精度。在桨模的瞬态振动分析中，为验证基于声信号的HHT算法识别模态阻尼比的准确性，人为设定前两阶模态阻尼比都为0.01。需说明的是，0.01并非是真实的阻尼比，人为设定该参数只是为了验证算法的准确性。螺旋桨模型直径为240 mm，盘面比约为0.74，带有30°侧斜角，材质为铝合金，根据质材检测报告，弹性模量为59 GPa，密度为2.7 t/m3。

2.1 桨叶的模态分析

通过有限元方法对桨叶进行正则模态计算，桨模叶根处采取刚固约束。计算结果如表1及图2所示。可见桨叶的第一阶模态振型是轴向弯曲振型，第二阶模态振型是弦向扭转振型。

表1 桨叶的前两阶固有频率

(a) 第一阶振型

2.2 桨叶在冲击振动下的近场噪声

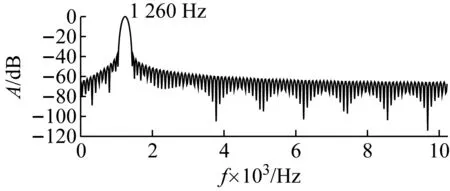
在桨叶正则模态分析的基础上，基于有限元瞬时振动响应计算方法，数值模拟桨叶中部受到单位冲击作用时的振动响应。在完成桨叶的瞬态振动计算之后，以桨叶表面的速度分布作为声学边界元的边界条件，进行瞬态声学边界元计算。计算总时长设置为0.05 s，计算时间步长为1/20 480 s。之后，在距离桨叶表面任意位置垂直距离2 mm处取场点1，提取声压信号，并通过HHT方法处理并识别模态参数。场点1采集到的声压信号的时域和频域曲线如图3所示。由于进行数值计算的总时长为0.05 s，经FFT之后的频率间隔最小为20 Hz，从图3中可见前两个峰值分别位于1 260 Hz和1 800 Hz，考虑频率分辨率，可大致确定前两阶固有频率分别处于1 240～1 280 Hz和1 780～1 820 Hz内。

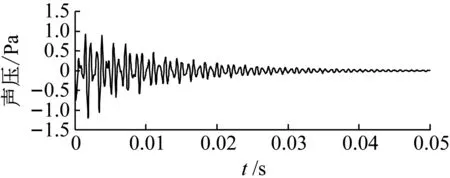
(a) 时域曲线

2.3 基于桨叶声信号的模态参数识别

在大致确定桨叶的前两阶固有频率的范围之后，通过Kaiser窗函数设计法设计有限脉冲响应(FIR)滤波器。FIR滤波器具有稳定及线性相位的优点[17]。针对桨叶第一阶固有频率，设计带通范围为1 240 Hz～1 280 Hz，对于桨叶第二阶固有频率，设计带通范围为1 780～1 820 Hz，设计阶数都为200。两个滤波器的幅值曲线如图4所示。

(a)

通过所设计的滤波器，分别对场点1的声压信号进行滤波处理。由于滤波后的信号存在相位延迟，还需要根据阶数进行相位的修正[18-19]。场点1的声压信号分别经过以上两个数字滤波器滤波及相位延迟修正之后结果如图5所示。

分别对滤波后的信号进行经验模态分解(EMD)，EMD分解后的第一阶固有模态函数(IMF)就是对应该阶模态的响应数据。分别对图5中的两组滤波后的信号进行EMD之后得到的第一阶IMF，如图6所示。

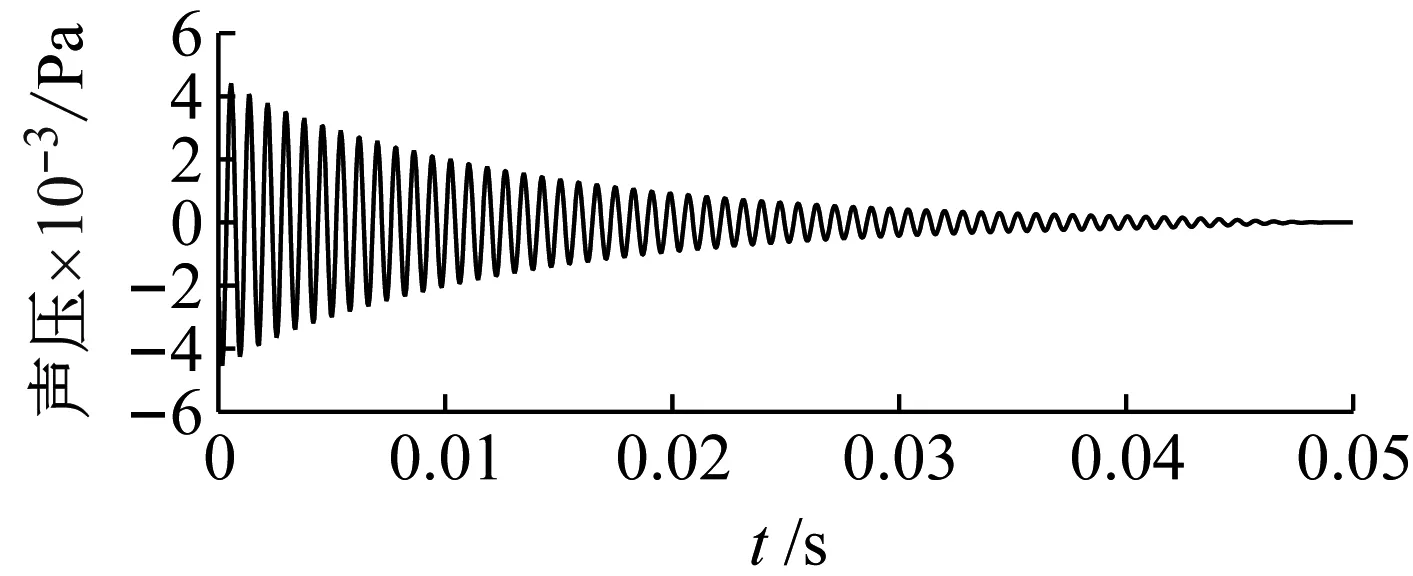
(a) 第一阶固有频率滤波结果

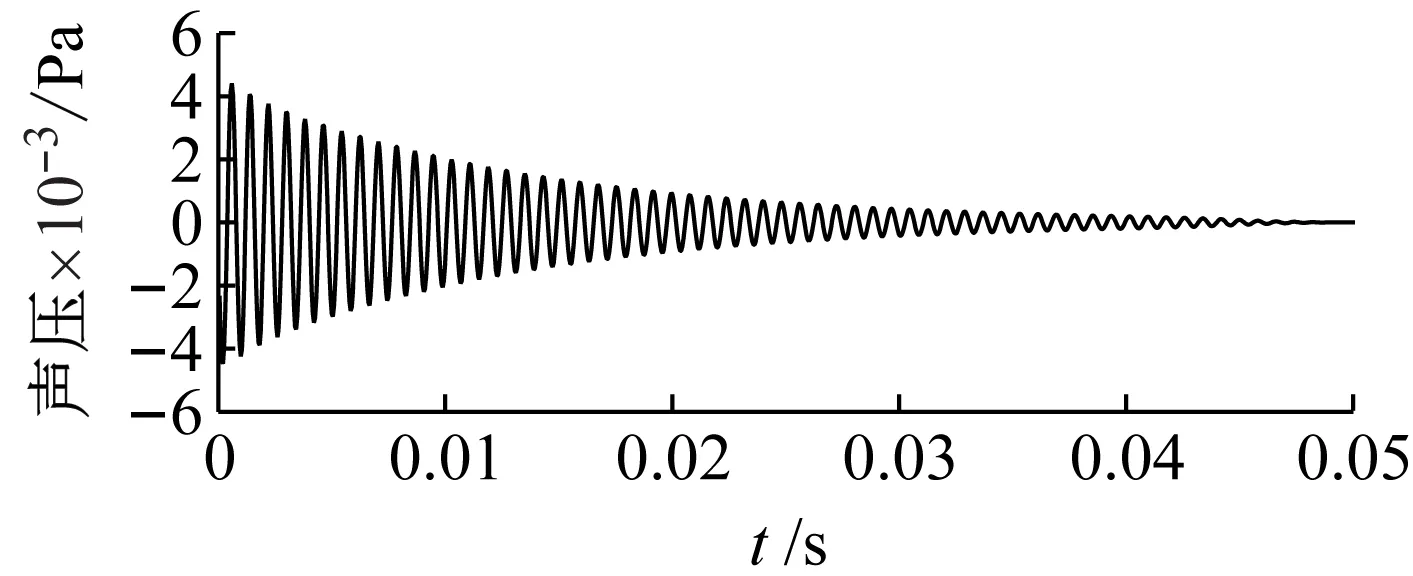
(a)

分别对图6中的前两阶模态响应信号进行希尔伯特变换(Hilbert transform，HT)，获得桨叶前两阶模态响应信号的瞬时幅值谱和瞬时相位谱，并对瞬时幅值谱取对数，绘制成曲线，并以最小二乘法线性拟合，结果，如图7所示。

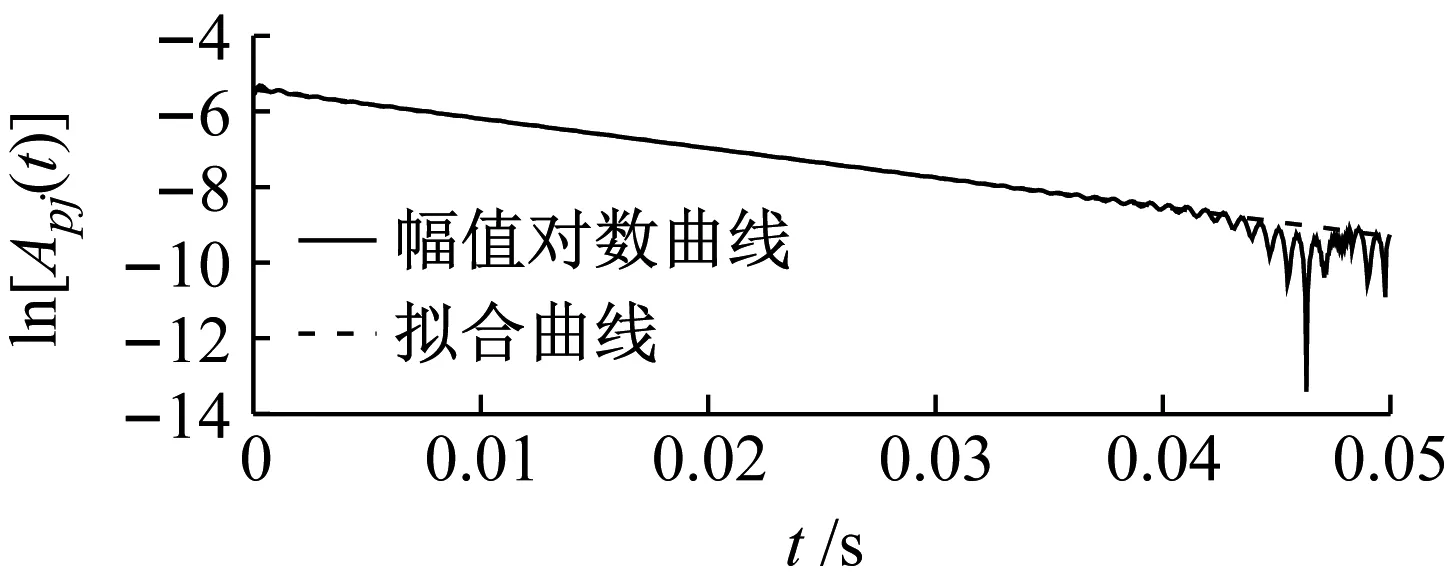
(a) 第一阶

由图7可见，瞬时幅值和瞬时相位曲线的端点存在严重的端点效应，这是由于前述数据的端点效应累计造成，包括使用FIR滤波器造成的端点数据失真和使用EMD分解造成的端点数据失真。对此，在进行最小二乘拟合时，去掉尾端部的一段数据，最终得到桨叶的前两阶模态参数如表2所示。

表2 桨叶前两阶模态频率与阻尼比

从计算结果可见，HHT方法可以很准确地识别桨叶前两阶固有频率和模态阻尼比，相比FFT方法，固有频率识别准确度更高，说明该方法具有很好的频率分辨率自适应性。此外，阻尼比识别结果非常准确，和数值解一致。

场点1位于表面附近，其声压信号主要受到邻近单元的影响，在文献[20-21]中，使用点声源模型表示其声压信号，其中源强为单元体积速度。本文中，式(16)建立了空间中任意场点和结构模态参数的关系，采样点不必要布置在近场。下面在距离桨叶较远的位置选取编号2～6共5个场点，分别是场点1沿着轴线方向平移100 mm，200 mm，300 mm，400 mm，500 mm得到(见图8)。以场点2～6的声压信号进行结构物的模态参数识别，结果如表3所示。

图8 距离桨叶较远的场点

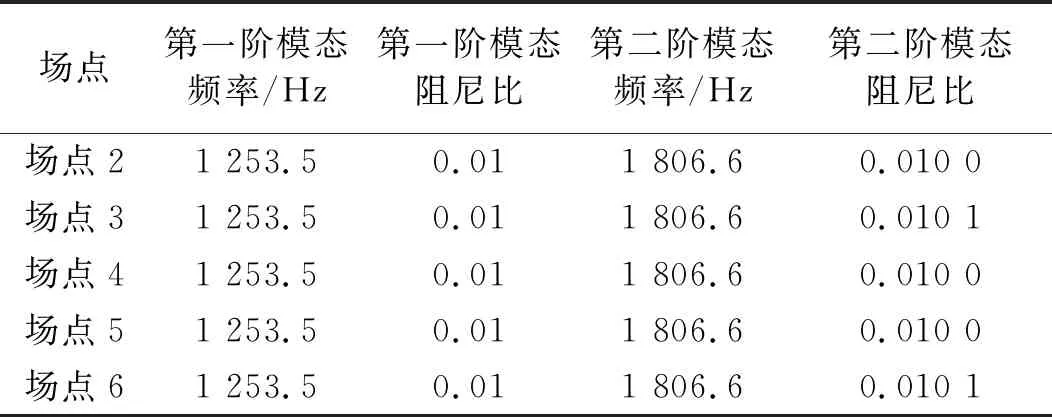
表3 场点2～6声压信号的结构模态参数识别结果

由表3可知，基于远场点的声压信号识别的桨叶模态参数依然具有非常高的准确度，其中固有频率的误差小于1‰，阻尼比最大误差为1%。当然，以上数据只是基于数值模拟，所采样的声压信号都是理想状态下的，不受实际环境噪声影响。为将该方法推广到实际工程应用中，还需要对环境噪声的影响进行评估。

2.4 环境噪声对于模态参数识别结果的影响

为评估环境噪声对于模态参数识别结果的影响，以桨叶的第一阶固有频率f1=1 253.5 Hz以及ζ1=0.01的阻尼比构建一标准衰减信号，表达式如下

(24)

以20 480 Hz的采样频率对该信号进行采样，采样时长0.05 s，得到一组标准衰减信号，另外，通过添加高斯白噪声方式来模拟环境噪声，并定义信噪比为1～10 240 Hz频带内的目标信号和噪声信号的总能量之比，如下

(25)

式中：ST为目标信号；N为噪声信号。通过设置白噪声信号的幅值，可将SNR大概限制在某一数值，可定量地评估信噪比对于模态参数识别精度的影响。以下研究信噪比分别为9 dB，6 dB，3 dB，0，-3 dB，-6 dB，-9 dB，-12 dB，-15 dB情况下模态参数的识别结果。需要说明的是：由于白噪声通过随机数算法产生，因此，对于某个信噪比，不一定能够精确达到，例如，目标信噪比为3 dB，实际信噪比可能是3.1 dB。由于白噪声的偶然性，因此，对于每一个信噪比下的模态参数识别仿真，都重复100次，取结果的平均值。以上不同信噪比下模态参数识别结果如表4所示；部分信噪比的时域曲线如图9所示。

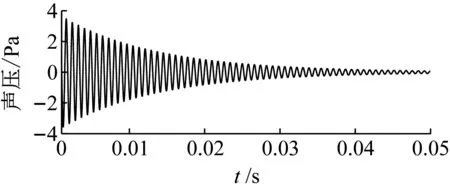
(a) 9 dB

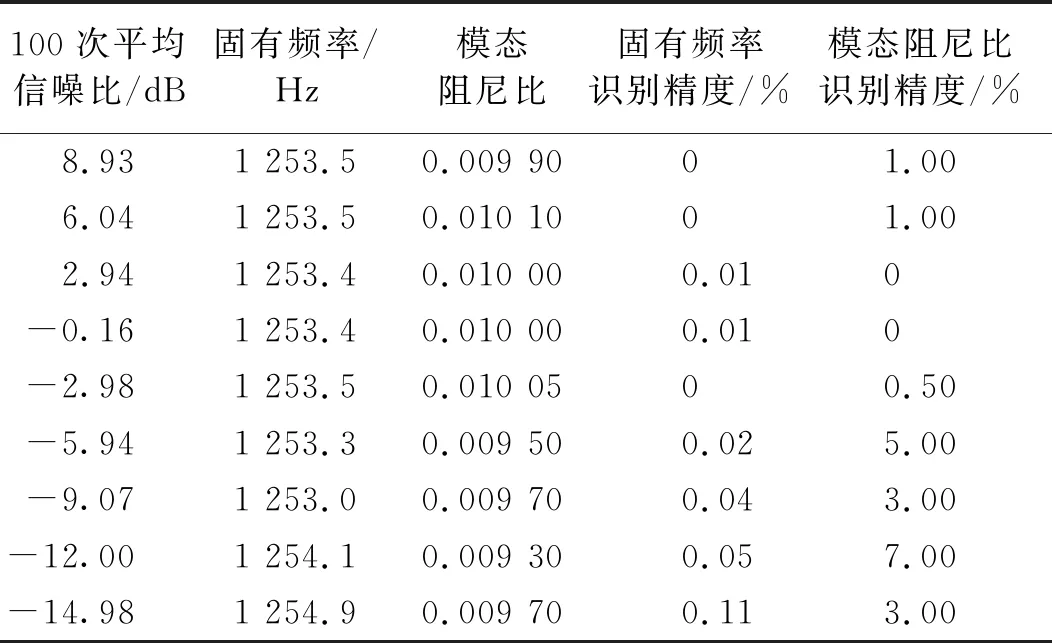
表4 不同信噪比的模态参数识别结果

由表4可知，随着信噪比降低，固有频率和模态阻尼比的识别结果精度都随之降低。其中，模态阻尼比的误差相对较大，相比之下，即使在较低的信噪比(-15 dB)下，固有频率的识别结果依然可以保证比较高的精度(0.11%)。相对而言，在低信噪比下，模态阻尼比存在较大的误差，这是因为模态阻尼比的数值比固有频率小5个数量级，在运算过程中，同样绝对值的误差会对模态阻尼比的计算精度造成更大的影响。

实际工程环境中，由于无法保证测量环境的全自由场属性以及无法避免背景噪声，所测量得到的信号会存在一定的噪声污染，本数值算例说明在相当低的信噪比之下，基于HHT方法依然可以较为准确地识别模态参数，证明该方法在工程应用中的实用性。

3 模型试验

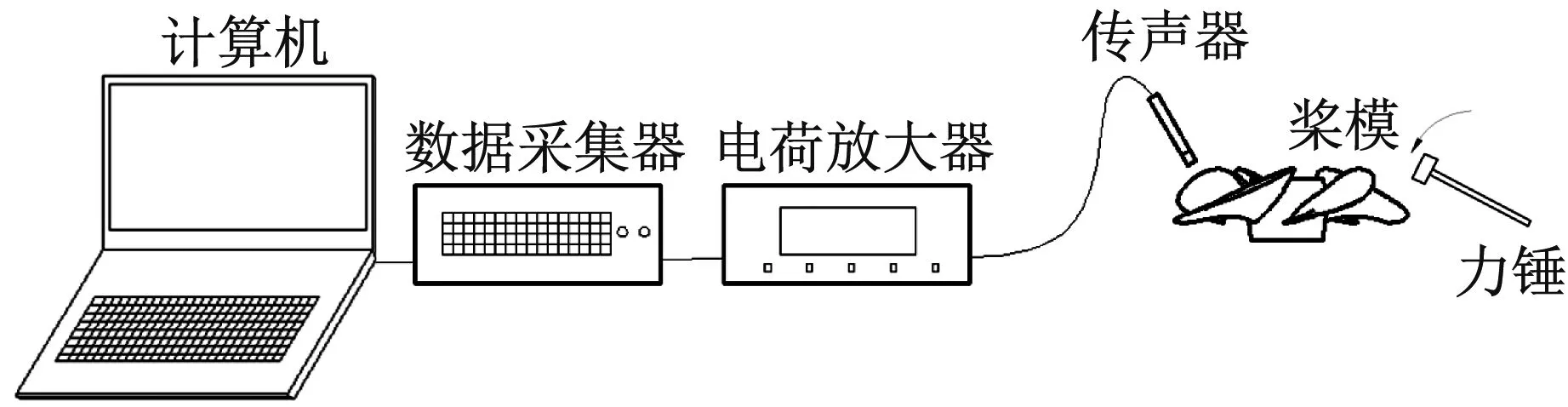
下面从试验角度对HHT方法识别模态参数的实用性进行验证。试验过程中，为实现较高的信噪比，传声器布置于桨叶压力面0.7倍半径弦长中部，与表面的垂直距离约为5 mm，通过力锤敲击桨叶梢部并同时记录声压信号。试验示意图和实景图如图10所示。传声器采集的声压信号如图11所示，采样频率为25 600 Hz，采样时长为1 s。

(a)

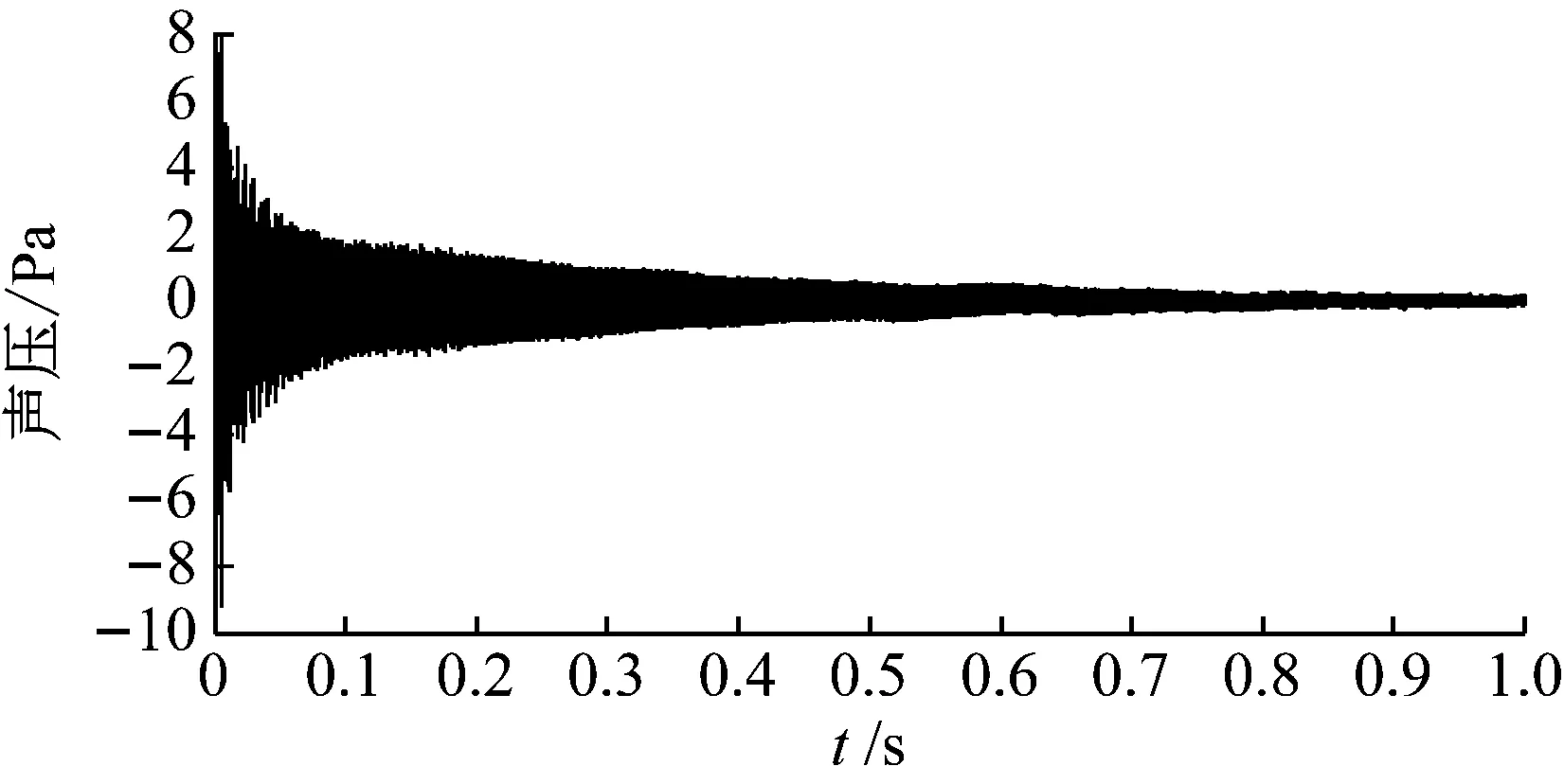
图11 传声器采集的声压信号

从原始信号中间位置截取一段进行分析，截取段样本长度为2 048。对于所截取的信号，通过1.2节中罗列的步骤进行处理，最终得到桨叶第一、第二阶固有频率和模态阻尼比，如表5所示。表5中将试验测量的固有频率和模态数值计算结果(见表1)进行了对比，结果显示试验和数值结果比较接近，第一、第二阶的差异分别为0.9%和2.7%。桨叶第一阶模态识别数据处理过程的部分曲线图如图12所示，由图12可知，对数幅值曲线存在小振幅的波动，而相位曲线则具有非常高的线性度，第二阶模态识别过程的相关曲线与第一阶类似。

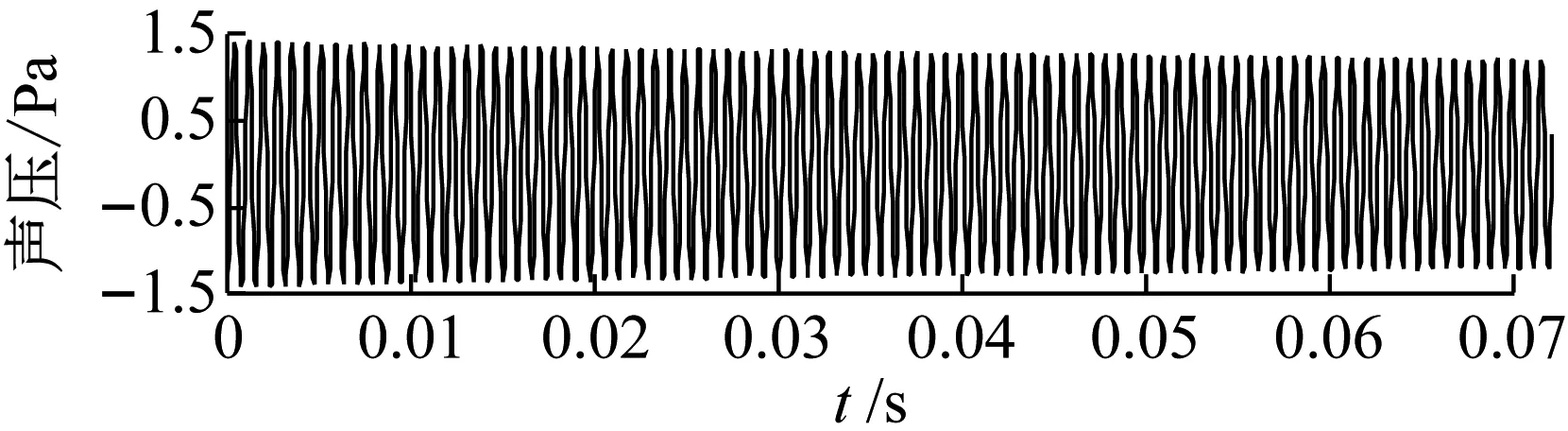
(a) 截取的信号段

表5 螺旋桨模态参数识别结果

4 结 论

本文通过自由场环境下外部直接声学边界元方法的推导，建立了结构振动时外场辐射声压和结构物模态参数之间的关系，相比于夏茂龙等和Xu等的研究在结构物近场提取声压信号进行模态参数的识别分析，从理论上阐明了在远场采集的声信号同样可以进行结构物模态参数的识别。在此基础上，通过数值仿真手段验证了所建立理论模型的远、近场适用性以及在较低信噪比下的准确性。最后，将该方法应用在一桨模的模态参数识别试验中，成功识别桨模的前两阶固有频率及模态阻尼比。本文的工作表明基于HHT算法的声信号模态参数识别方法可为桨模等精细结构的模态参数识别提供一种新的途径。