切丝机清洗设备超高压缸体的应力计算研究

杨光露，宋俊奇，吴会营，姚建松，鲁中甫，刘穗君

(1.河南中烟工业有限责任公司，河南 郑州 450000)(2.郑州轻工业大学电气信息工程学院，河南 郑州 450002)

切丝机铜排链清洗是烟草设备维护的棘手问题[1]，铜排链在使用一段时间后，表面会粘附一层烟草的汁液，如何高效地去除这层黏附的汁液是现场作业人员面临的问题。经过试验发现，采用超高压水冲击洗刷铜排链的表面效果良好。超高压缸是铜排链清洗高压泵的关键部件，超高压缸体缩套式结构采用的是工程上常用的能提高缸体承压能力、减小缸体厚度、提高缸体安全性的方式，其他还有用钢丝缠绕、整体结构自增强产生预应力的方式来提高缸体的承压能力[2-3]。国内外很早就对超高压缸进行了一些研究，张于贤等[4]基于弹塑性超高压缩套缸体理论，建立了存在同轴度偏差的双层缩套缸体数学分析模型；王红等[5]根据相关自增强理论，对超高压缸进行了优化设计，在质量、外观及应力分布等方面进行了较大的改进；Lee等[6]对自增强复合材料圆筒进行了残余应力分析，通过提高高压缸体的残余应力来提高其承载能力和疲劳寿命。但目前对双层缩套式超高压缸的有限元分析和数值计算的研究较少。

本文以超高压缸为研究对象，结合有限元分析和数值求解的方法，得出双层缸体在预应力状态和工作状态下的应力分布情况。研究表明，双层结构套合的缸体与单层缸体相比，其承压能力增加两倍，对多层组合圆筒进行自增强加工，可使其承受更高的工作压力。

1 高压缸体理论分析

超高压清洗机需要的水柱压力高、冲击力大，因此对高压缸体提出了较高的设计要求[7-8]。高压缸体要承受250～600 MPa的内压，且水的流量较大，传统方法采用单层缸体制造，需要较厚的缸体，体积大、质量重、应用不便。若采用双层缩套式超高压缸体，可有效减小缸体的厚度[9]。

1.1 挤压筒内孔型腔基本理论研究

挤压筒在挤压过程中承受三种力，即径向压力、周向压力和轴向压力，挤压过程中沿轴向的应力分布相对均匀，因此可以将挤压筒简化为等壁厚圆筒，采用解决平面应变问题的方法，基于弹性力学计算得出双层缸体的接触应力和受内压时的应力应变[10]。

1.2 高压缸体弹性力学基本方程

壁厚相同且较长的圆筒，其内表面和外表面承受径向均匀分布的压力，假设沿筒轴方向的压力相同。根据轴对称的弹性力学平面应变理论，由于压力和物体都具有对称性，变形后的圆筒轴线也是对称的，因此当采用极坐标时不存在切向位移和剪应力。受内压的单层缸体如图1所示，受外压的单层缸体如图2所示。

图1 受内压的单层缸体

图2 受外压的单层缸体

在极坐标系下，受压缸体应变与位移的微分关系式为：

(1)

式中：εr为径向应变分量；εθ为周向应变分量；γrθ为切向应变分量；u为位移；r为半径。

弹性力学中圆形平面问题的平衡微分方程简化式为：

(2)

式中：σr为径向应力；σθ为周向应力。

由于圆筒轴线对称，采用极坐标时不存在切向位移和剪应力，此时轴向应力σz=0，受压缸体应力应变关系式(1)可整理为：

(3)

由式(3)整理可得到：

(4)

式中：μ为圆筒材料的泊松比；E为弹性模量；τrθ为切向应力；G为剪切模量。

将式(4)代入式(2)中计算得：

(5)

将应变与位移的微分关系式(1)代入式(5)计算得：

(6)

经计算得到最终解为：

(7)

(8)

式中：C1,C2为积分常数，由边界条件决定。

经过以上推导，得到预应力状态和工作状态下的理论计算公式：

(9)

式中：pi为单层缸体所受内压力；po为单层缸体所受外压力；R1为内筒内径；R2为外筒外径；R12为双层缩套缸体的分界半径；p12为内外筒体间的缩套界面压力；GY为过盈量；K1为内筒外径与内筒内径之比；K2为外筒内径与内筒外径之比。

2 高压缸体数值计算及结果对比

2.1 建立有限元模型

双层缩套式圆筒模型为轴对称模型，为了避免绘制模型时出现交叉封闭区域，直接使用Workbench附带的Design Modeler模块完成对双层缩套式圆筒的参数化建模。以某公司生产的超高压缩套式缸体为例，其双层圆筒尺寸参数见表1。

表1 双层圆筒尺寸参数 单位：mm

定义材料参数：在Engineer Data 中设定材料特性，缸体材料为0Cr17Ni4Cu4Nb，泊松比λ=0.26，弹性模量E=211 GPa，屈服强度σs=863 MPa，抗拉强度σb=990 MPa。对于双层套筒，当通过加热外筒体将其套到内筒体上，温度下降后，在内外筒体之间会产生一定的压力，此压力即为缩套压力pc。该压力使内筒体受压缩，外筒体受到拉伸。因此界面处外筒内壁由于界面压力的作用产生的径向扩张量u0加上内筒外壁受界面压力的外压作用产生的径向收缩量ui，即为内外筒总的变形量，此变形量称为缩套过盈量Δ，Δ=ui+u0。通过这些关系可求得缩套界面压力。

模型的内筒和外筒相互接触，可以形成有限元接触对，接触的方式为面对面接触，目标面为内筒外壁，接触面为外筒内壁。将惩罚系数设定为0.2，能够获得更好的收敛性，接触刚度矩阵为对称矩阵。利用Frictionless Support指令对内筒施加边界条件，内筒沿Y方向的自由度为零。在完成模型的材质定义后，可以使用自由网格对模型进行网格划分，充分考虑模型求解的精度和速度，令Element Size为0.000 7 mm，超高压缸体有限元模型分为3 260个单元，10 219个节点。双层超高压缸体有限元模型如图3所示。

图3 双层超高压缸体有限元模型

2.2 加载和求解

将加载求解过程分为两个载荷步：预应力状态和工作状态。位移、压力加载曲线如图4所示。第一步，对外筒施加位移载荷，使内外筒之间产生预设的过盈量，打开大变形效应和自动时间步，然后展开求解；第二步，对内筒按载荷步有序施加610 MPa的内压力，有效模拟超高压缸体的工作状态。程序设置如下：载荷子步为40，最小子步为15，最大子步为 55。按以上参数设置进行求解。

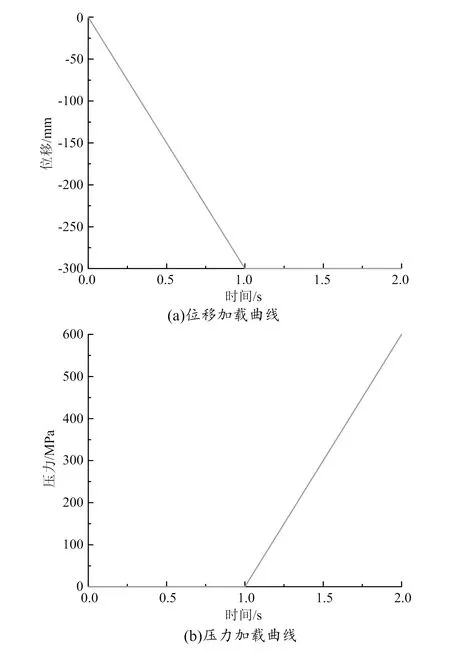
图4 位移、压力加载曲线

2.3 数值计算

预应力状态下等效应力线如图5所示，由图可以看出，内筒内壁到内筒外壁的等效应力是逐渐减小的，在内筒外壁和外筒内壁相互接触的位置突然发生变化，外筒内壁到外筒外壁的等效应力也是逐渐减小的。

图5 预应力状态下等效应力线图

工作状态下等效应力线图如图6所示，由图可以看出，工作状态下的等效应力从内筒内壁到内筒外壁是逐渐减小，在内筒外壁和外筒内壁相互接触的位置突然发生变化，外筒内壁到外筒外壁等效应力也是逐渐减小的。

图6 工作状态下等效应力线图

2.4 理论计算和数值分析结果

表2和表3所列为预应力状态下缸体不同位置周向应力和径向应力的理论计算和有限元仿真结果，由表可看出，预应力状态下有限元仿真和理论计算的结果几乎是一致的。表2～表5中应力值为负代表压应力，对应压应变；应力值为正代表拉应力，对应拉应变。

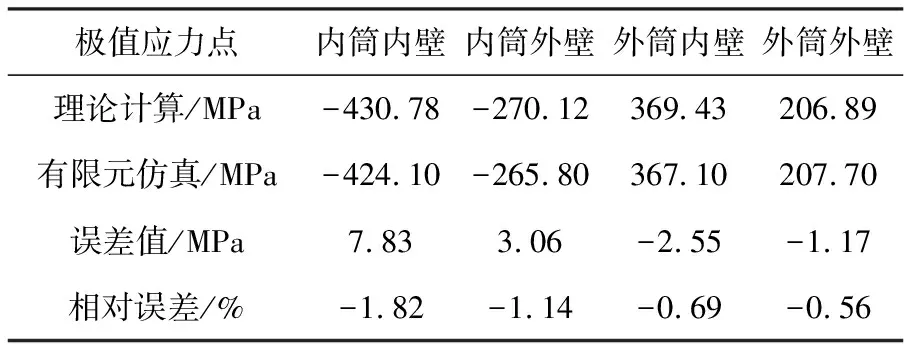
表2 预应力状态下缸体不同位置周向应力值对照

表3 预应力状态下缸体不同位置径向应力值对照

表4和表5所列为工作状态下缸体不同位置周向应力、径向应力的理论计算和有限元仿真结果，由表可看出，工作状态下有限元仿真和理论计算的结果几乎是一致的。

表4 工作状态下缸体不同位置周向应力值对照

表5 工作状态下缸体不同位置径向应力值对照

从表4和表5可以看出，在工作状态下，无论是周向应力还是径向应力，缸体内筒内壁和外筒内壁一直为应力集中位置，从内筒内壁到外筒内壁应力的变化率为0.789 MPa/mm，即超高压缸体的应力分布不均匀，因此在设计超高压双层缸体时需要考虑对缸体结构进行优化。

2.5 实验结果

在进行切丝机清洗设备超高压缸体研究过程中，设计了一种测定超高压缸体应力的实验方法。通过溢流阀、压力表、加压设备等的配合作用，测出了预应力状态下缸体相应位置的周向应力和径向应力，见表6和表7，工作状态下缸体相应位置的周向应力和径向应力，见表8和表9。

表6 预应力状态下缸体不同位置周向应力值 单位：MPa

表7 预应力状态下缸体不同位置径向应力值 单位：MPa

表8 工作状态下缸体不同位置周向应力值 单位：MPa

表9 工作状态下缸体不同位置径向应力值 单位：MPa

该实验数据与理论计算、数值分析的结果基本吻合，说明模型可以用于实际工程。

3 结束语

本文以超高压清洗设备的关键部件超高压缸为研究对象，采用有限元分析和数值求解方法，求出双层缸体在预应力状态和工作状态下的应力分布情况，并对两种方法获得的结果进行比较和验证。结果显示，两种方法的计算结果高度吻合，表明所建立的有限元模型是合理的，求解方法是正确的。

双层缸体相比单层缸体能够有效降低应力峰值，使缸体内部的应力分布更为均匀，缸体材料得到更有效的利用。在同样的工作压力下，能够以更薄的缸体厚度保证使用的安全性，减少材料的用量和缸体体积，是降本增效的设计方向。