一种保细节特征的点云多尺度三角网格重建算法

吴 科，姜晓通,，邓 昊，程筱胜，崔海华，刘宁钟

(1.常熟理工学院机械工程学院，江苏 常熟 215500)(2.南京航空航天大学计算机科学与技术学院，江苏 南京 210016)(3.南京航空航天大学机电学院，江苏 南京 210016)

三维点云三角网格重建是数字化技术的重要组成部分，在许多领域有着广泛的应用。物体表面的三维缺陷通常是微小的，表面微小缺陷检测是计算机视觉技术在工业领域里的重要应用，如何从扫描得到的点云数据重建出这些微小缺陷是网格重建技术的难点。

根据三角网格重建技术的原理，现有的网格重建技术主要分为基于隐式曲面的网格重建和基于计算几何的网格重建。基于隐式曲面网格重建是借助隐式函数对点云数据局部或全局进行拟合或插值[1-2]。隐式曲面重建算法具有较强的鲁棒性，然而其重建原理决定该方法对数据细节特征的表达具有先天的缺陷。基于计算几何的网格重建是从几何的角度出发实现点云数据的三角网格化，通过构造点云的Delaunay三角剖分来构建点与点之间的拓扑关系。实现Delaunay三角剖分的方法有很多，最具代表性的算法有Voronoi/Delaunay算法[3-4]和区域增长法[5-7]。Voronoi/Delaunay算法由于时间复杂度和空间复杂度较高，因此该算法并不适合商业应用。区域增长法是目前商业软件中最常用的三角网格重建算法，该算法从种子三角形开始逐层向外扩张，直到完成整个点云数据的三角网格重建为止。旋转球算法[5](ball-pivoting algorithm，BPA)是最经典的区域增长法，该算法生成的三角网格满足Delaunay剖分。然而由于旋转球的半径是定值，该方法在重建时会产生很多孔洞或出现局部细节丢失等情况。Digne等[6]利用平均曲率移动(mean curvature motion，MCM)算法将点云从高频点云数据空间变换到低频点云数据空间中，实现细节特征的高保真重建；张长东[7]采用变半径搜索方法有效地避免了由于点云数据局部不均导致的孔洞问题。

本文结合文献[6]和文献[7]的优点，提出了一种多尺度、自适应半径的网格重建算法，在实现点云数据细节特征高保真重建的同时，减少了网格孔洞的出现。

1 算法流程

图1所示为本文三角网格剖分过程的二维示意图。首先在网格重建前，将点云数据从高频尺度空间变换到低频尺度空间中，如图1(b)所示；然后在点云数据的低频尺度空间中，利用自适应半径的区域增长法实现点云数据的三角网格化，如图1(c)～图1(e)所示；最后在保持网格拓扑不变的情况下，将低频尺度空间数据映射回高频尺度空间，完成点云的三角网格化，如图1(f)所示。

图1 三角网格剖分算法流程

2 低频点云数据获取

2.1 平均曲率移动

如图2所示，假设S是在i3空间中R2连续的光滑曲面,p是曲面上一点，其法矢为n(p)。垂直于点p处的切平面，t(p)是位于该切平面内且通过点p的一个切向量。n(p)和t(p)张成一个平面Q，平面Q与曲面S相交形成一条曲线l，曲线l在点p处的曲率为k。由于在曲面S上过p点有无数个切向量，其对应无数条曲线，这些曲线在点p处的曲率必定有一个最大值kmax和最小值kmin，分别称为最大主曲率和最小主曲率，则曲面S在点p处的平均曲率为H(p)，H(p)=1/2(kmax+kmin)。

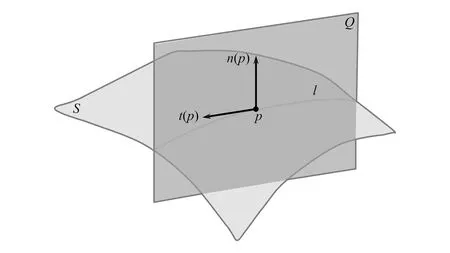
图2 曲面S上一点的主曲率

对于一组点云数据，文献[6]采用MCM对该组点云数据进行光顺，MCM可以表示为：

(1)

式(1)的几何意义为点p以与该点处平均曲率H(p)成正比的速度沿着该点的法矢(n(p))方向移动。

2.2 离散点云数据平均曲率移动

文献[8]提出了针对MCM的近似算法，该算法将点云中的每一个点通过多次迭代投影到该点所在的局部“退化”平面上，该迭代投影能够保证得到鲁棒的几何信息。算法1为离散点云数据MCM的计算方法。

算法1 一次MCM移动

输入：P，为一组点云数据；p，为点云中的一个点；r，为半径；n，为给定的正整数

输出：p′，为点p经MCM计算后的结果

1)以r为半径，计算点p的一组邻域点Nr(p)；

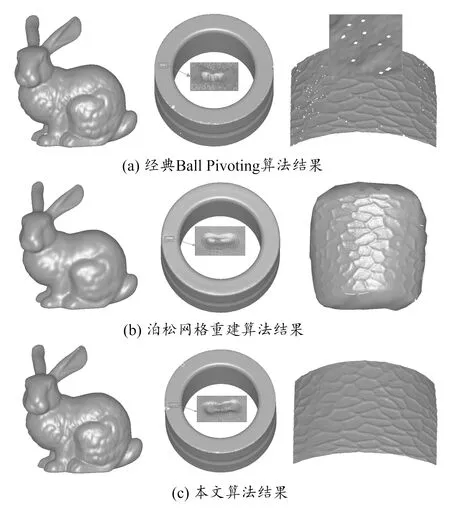
2)if|Nr(p)|

3)Removep;

5)Calculating eigenvectorv0, who corresponding to the least eigenvalue ofC；

7)n(p′)=v0·sign(v0·n(p))。

算法1在对点云数据进行MCM操作前，需要对点云数据法矢n(p)进行初始化，并保证法矢方向连续。下面介绍算法1中的关键步骤：

Line 1)：采用八叉树搜索点的邻域，在计算邻域点时，要考虑邻域点的个数，保证后续法矢计算及移动方向的准确。

Line 2)和3)：如果一个点周围邻域点的个数小于n，则在计算时将不考虑该点，本文n取值4。

Line 4)：ω(q)为点p邻域点q的权重，其计算公式为：

ω(q)=exp(-‖p-q‖2/(2r2))

(2)

Line 7)：经过MCM移动后，更新点p移动后的点p′的法向量n(p′)，n(p′)应与v0平行，方向与点p的法矢n(p)方向的夹角应该小于90°，由sign(v0·n(p))保证。

在实际计算过程中，本文算法通过4次迭代，将点云数据从高频空间转换到低频空间，计算结果用于后续的三角网格重建，以提高重建质量。

3 自适应半径区域增长法网格重建

区域增长法是最常用的一种三角剖分算法，其重建过程中没有费时的迭代过程，算法效率高，适用于数据量大的点云数据，很多商业化逆向工程软件都采用该方法进行网格重建。

3.1 种子三角形定义

种子三角形是区域增长法的起始三角形，确定合适的种子三角形是区域增长法的第一步。种子三角形选取的方法有很多，大多数方法是在点云数据中随机选取一个点及其邻近两个点来构造种子三角形[5, 9-10]，这些方法简单易行，但在处理不均匀或存在噪声的点云数据时，种子三角形有可能位于异常区域，导致三角网格重建质量难以保障[7]。Li等[11]在点云数据中随机选取多个种子三角形，通过判断每个种子三角形周围三角形法矢的变化情况，将法矢变化最小的种子三角形作为起始三角形。该方法虽能在一定程度上保证种子三角形的质量，但较为繁琐。本文采用文献[7]中的方法定义种子三角形，该方法的流程如下：

1)从点云中随机选定一点pi。

2)利用八叉树算法查找与点pi距离小于r的点集N(pi)，若N(pi)为空，则重新选取随机点，继续查找。查找半径通过计算点云的平均点距得到，即：

(3)

式中：(xmax,ymax,zmax)和(xmin,ymin,zmin)分别为点云数据包围盒的两个极值点；m为点云中点的个数。

3)从邻近点集N(pi)中选取两个点pj和pk，满足以下条件：

①pi,pj和pk不在同一条直线上；

②过pi,pj和pk三点的球内不包含N(pi)中的任意其他点；

③N(pi)中的任意其他点都在Δpipjpk的同一侧。

4)若上述步骤执行完毕后仍未找到合适的种子三角形，则返回1)重新选择。

3.2 计算最佳点

在确定种子三角形后，从种子三角形开始，以种子三角形的一边为基础，计算最佳点，形成新的三角形。在计算新的三角形时，记种子三角形的一条边为活动边，搜索该活动边的邻域点，作为形成新三角形的候选点集。候选点集的数量会影响网格重建的效率及质量，若候选点集过多，会降低重建效率，同时也会在网格边界产生狭长三角面片，降低重建质量；若候选点集过小，容易产生较多的孔洞。现有的方法大多采用固定半径搜索方法[12]，但当点云数据不均匀时，在点云密度较小的区域极易出现孔洞。为了解决这一问题，本文提出了一种自适应半径搜索方法。假设计算包含边pipj的新三角形，该方法的具体步骤如下：

1)在已三角化的网格中，搜索包含点pi和点pj的所有边，如图3(a)所示，并计算所有边的长度；

在确定搜索半径后，以pipj的中点pm为球心、r为半径画球，则位于球内且没有被网格化的点或位于边界上的点作为新三角形的候选点，图3(a)中虚线内的点即为候选点。

图3 最佳点计算

在确定候选点后，需要确定最佳的候选点，与当前活动边生成新的三角形。为了保证重建网格的质量，所确定的最佳候选点应该尽量满足Delaunay三角剖分准则，同时最佳候选点所确定的三角形的法矢应与其相邻三角形法矢的变化尽可能小。本文采用文献[12]中代价函数评价每个候选点的代价，在计算完所有候选点的代价后，按照代价从小到大的顺序依次对新的三角形进行质量检测，直到新的三角形符合要求为止，则代价最小且符合要求的候选点即为所确定的最佳点。在进行质量检测时，主要检测新的三角形是否存在非流行及自交的情况。确定新的三角形后，将新的三角形加入到存储网格数据的特定拓扑结构中。

4 实验结果

为了验证算法的有效性，本文主要从网格质量及重建效果的角度来对算法进行评估。网格的质量通过网格孔洞数和自交三角形个数来进行评估，重建效果则通过点云数据重建率(网格重建后点的数量与原始点云中点的数量之比)及重建后细节特征来评估。测试数据包括经典的Bunny数据、轴承表面点云数据、玻璃器皿表面点云数据。其中，轴承表面点云数据中包含轴承表面微小三维缺陷，玻璃器皿表面点云数据包含浅浮雕花纹。对比的算法分别为经典的Ball Pivoting算法和泊松网格重建算法。

图4分别为上述3种算法的重建结果。从图可以看出，经典的Ball Pivoting算法在重建微小细节特征时，若球半径较大，细节特征丢失较严重，如图4(a)第二幅图片所示；若球半径过小，则会出现较多孔洞，如图4(a)第三幅图片所示。泊松网格重建算法因为其重建是以局部逼近拟合的方式来重构表面网格数据，因此其细节特征丢失较为明显，如图4(b)第一、二幅图片所示，同时由于其重建结果是水密的网格，因此在重建曲面点云时会生成封闭网格，如图4(b)第三幅图片所示。本文算法是在点云数据的低频尺度空间中进行网格重建后再映射回高频尺度空间，因此本文算法对细节特征的重建结果较好。

图4 算法比较

表1为本文算法与经典的Ball Pivoting算法重建质量及效果比较，评价指标分别为网格孔洞数a、自交三角形个数b以及点云数据重建率c。由于泊松网格重建算法的原理决定其重建结果中不会出现孔洞、自交三角形，并且重建后网格中点的个数主要取决于其重建过程中点云空间划分最小单元格的大小，因此本文不做比较。从表中可以看出，与经典的Ball Pivoting算法相比，本文算法点云数据重建率较高、网格孔洞数较少。但本文算法在网格重建完成后需要从低频尺度空间映射回高频尺度空间，映射可能会导致在点云移动较多的区域产生三角面片相交的情况。因此在进行点云MCM操作时，如何保持点云中点的邻域信息不变是防止产生三角面片自交的关键。

表1 不同算法三角网格重建质量及效果比较

5 结束语

本文提出了一种多尺度、自适应半径的网格重建算法，在点云数据的低频尺度空间中进行三角网格重建，结合自适应半径的区域增长算法，实现点云数据高质量的重建。实验结果表明，与经典Ball Pivoting算法、泊松网格重建算法相比，本文算法的重建质量较高，并且能够较好地保持网格细节特征。

本文算法虽然在重建质量上有较大提高，但该方法在向低频尺度空间变换时，可能会改变点的邻域，邻域的改变会导致网格在映射回高频尺度空间后，网格局部三角面片自交。因此，如何在进行MCM操作后仍保持点云数据中点的邻域信息不变，减少重建后网格的自交，是后续研究的重要内容。