带法向约束的圆平均非线性细分曲线设计

刘艳，寿华好，季康松

浙江工业大学理学院，杭州 310023

0 引 言

在CAGD(computer-aided geometric design)和CG(computer graphics)中，点云曲线曲面重建是一个广泛研究的问题。通过采样设备获取测量数据，并对其进行数据拟合，可以实现对原模型进行大致的重建及功能恢复。但有些情况下，获取的数据点可能不只是简单的坐标信息，可能包含一些几何约束(任浩杰 等，2022)，如在光学工程领域对带法向约束的数据点进行光学反射面设计。

与NURBS(non-uniform rational B-splines)相比，细分允许设计高效的、分层的、局部的和自适应的算法，用于建模、绘制和操作任意拓扑的自由形状的对象。细分是不断插入新的顶点，更新旧的顶点，从而得到光滑曲线曲面。根据细分规则，细分曲线可分为线性细分与非线性细分。经典的线性细分曲线有Chaikin割角曲线(Chaikin，1974)、4点插值细分法(Dyn等，1987)及其推广(Hassan等，2002；郑红婵 等，2004)和单参数3点ternary插值细分(郑红婵，2003)。线性细分通常易于实现，细分规则较为简单，易分析其收敛性与光滑性，但是产生的极限曲线易有拐点，曲率变化大，并且很难重现圆。

为了克服线性细分法的缺陷，非线性细分法得到广泛关注。Ding和Hua(2000)提出具有保凸性的非线性4点插值曲线。Yang(2006)提出非线性基于法向量的曲线细分法，Dyn和Hormann(2012)以及Zhang和Zhang(2010)在此基础上做了改进。Deng和Wang(2010)提出一种基于双圆弧插值的中心细分法，Deng和Ma(2012，2014)对其进行了改进。Mao等人(2016)利用三次Bézier 曲线提出了基于法向量的快速曲线曲面插值细分方案。在此基础上，Lipovetsk(2022)提出了基于Bézier平均的非线性细分法。Zhang等人(2020)提出一种带张力参数的任意度非线性广义细分法。Bellaihou 和 Ikemakhen(2020)提出一种在空间单位球上生成曲线的非线性几何细分法。Lipovetsky和Dyn(2016，2019)提出一种新的基于圆平均的4点非线性细分法和L-R(Lane-Riesenfeld)算法，并证明了它们的收敛性与连续性。李彩云等人(2019)提出基于圆平均的带参数4点插值细分与3点逼近细分。在此基础上，本文提出基于圆平均的双参数4点binary细分法与单参数3点ternary插值细分法。其中，基于圆平均的双参数4点binary细分法是基于圆平均的带参数4点插值细分的推广(李彩云 等，2019)，增加了偏移参数μ。此外，本文首次提出将圆平均应用到ternary插值细分，这使得细分过程中控制顶点的增加速度更快。

本文针对有法向量的初始控制顶点，将线性细分法改写为点的重复binary平均，并用圆平均代替线性平均，用加权测地线平均(Dyn和Sharon，2017)算出的法向量作为新插入顶点的法向量，从而得到两种基于圆平均的非线性细分法，并给出了收敛性与连续性的证明。数值例子表明，本文的4点细分法比李彩云等人(2019)提出的4点细分更加灵活，与相应的线性细分相比，具有更强的曲线造型能力，同时具有圆的再生力；本文的3点ternary细分法在实现插值的同时，每一次细分获得的控制顶点是上一次控制顶点的3倍，这使得细分过程中控制顶点的增加速度更快，同时，也具有圆的再生力。

1 理论与方法

1.1 圆平均

1.2 加权测地线平均

在圆平均中构造的新点的法向量nω是n0与n1的加权测地线平均(Dyn和Sharon，2017)。对于单位法向量n0=(cosα,sinα)与n1=(cosβ,sinβ)的加权测地线平均定义为G(n0,n1;ω)=(cosγ,sinγ)，其中，α，β，γ是与直角坐标系横坐标轴的夹角且γ=(1-ω)α+ωβ。

本文的带法向约束的圆平均非线性细分法均是在点—法向量对上进行操作，且法向量是基于测地线平均的，独立于点的平均。证明本文细分法的收敛性即证明点和法向量的收敛性，主要依据下面的引理1(Dyn和Sharon，2017)与引理2(Lipovetsky和Dyn，2016)。

引理1 设T为适用于流形数据的测地线细分法。如果T有收缩因子，那么T是收敛的。

引理2 细分法的加细顶点对于任意的控制顶点收敛，如果任何顶点序列满足：

2 基于圆平均的双参数4点binary细分法

2.1 本文的双参数4点binary细分法

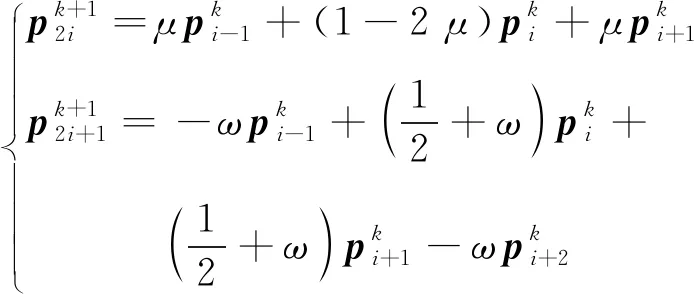
(1)

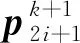
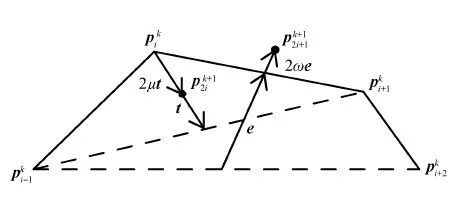
图1 线性双参数4点binary细分法的细分过程

(2)

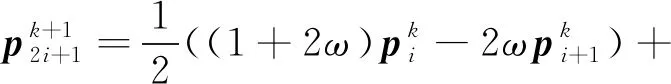
(3)

可以看出，线性双参数4点binary细分法每一次细分由偏移步与张力步两步骤组成。用圆平均代替式(2)和式(3)的线性平均，可以得到基于圆平均的双参数4点binary细分法。与线性双参数binary细分法类似，本文的双参数4点binary细分法每一次细分也是由偏移步与张力步两步骤组成，如图2所示。本法μ=0时的细分法是李彩云等人(2019)提出的基于圆平均4点插值细分法的一个特例。

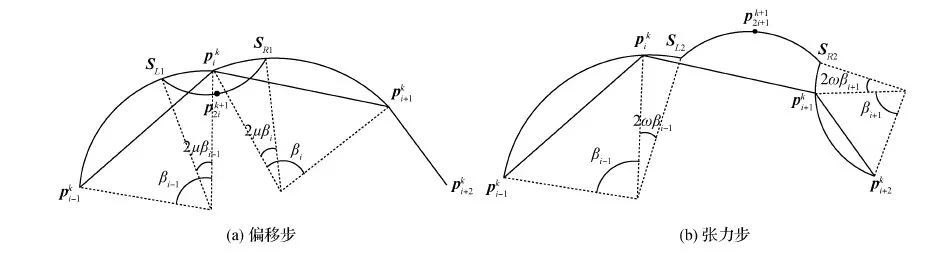
图2 本文的双参数4点binary细分法的细分过程

算法1 基于圆平均的双参数4点binary细分法。

输入：初始控制点及其法向量Pi=(pi,pi),i∈Z。

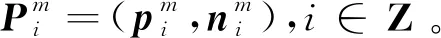
2)对于k=0,1,2,…,m;

执行∀i∈Z;

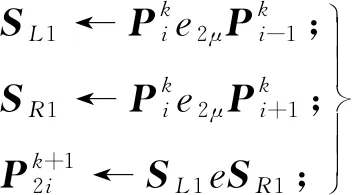
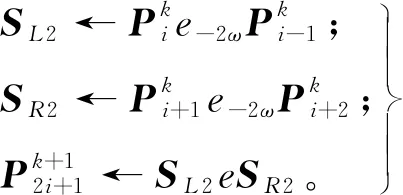
2.2 收敛性

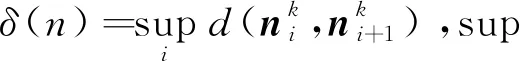
由三角不等式，有

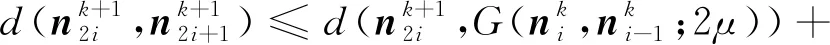
(4)

式中，

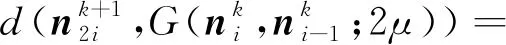
(5)

(6)

(7)

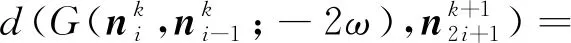
(8)

对式(5)和式(8)再次应用三角不等式，有

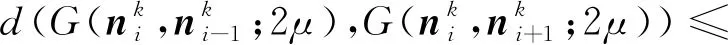
(9)

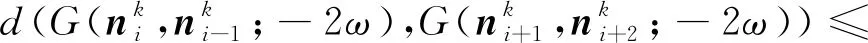
(10)

由式(4)—(10)，有

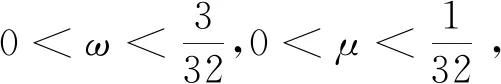
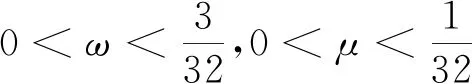
由三角不等式，得

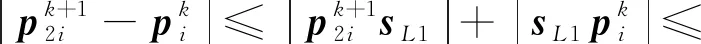
(11)

(12)

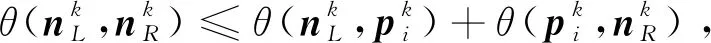
下面对|sL1sR1|进行估计

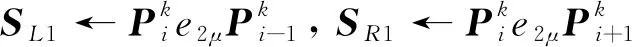
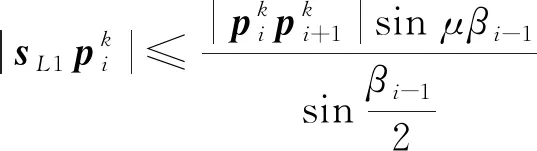
因此

(13)

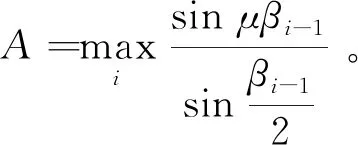
将式(13)代入式(11)，有

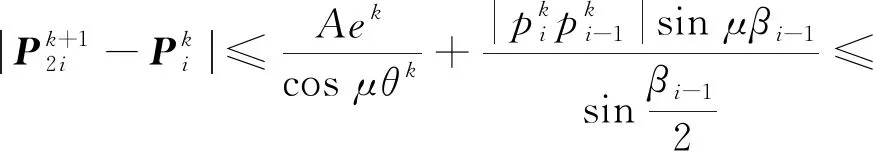
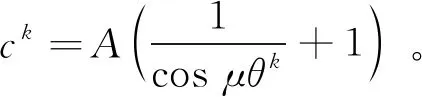
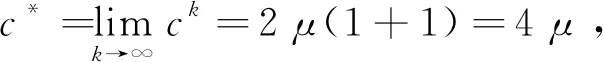
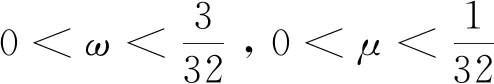
证明：由三角不等式，得

(14)

式中，

|sL2sR2|≤ek(1+2B)(李彩云 等，2019)

(15)

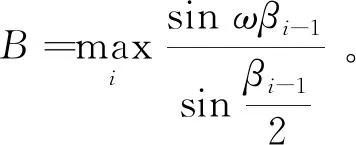
将式(13)和式(15)代入式(14)，得

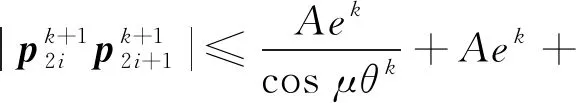
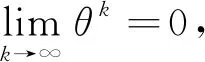
(16)

证明：由引理4和引理5可以得到点的收敛性，再由引理3，可以得到本文的基于圆平均的双参数4点binary细分法是收敛的。证毕。

2.3 连续性

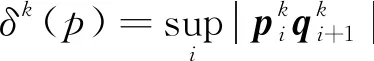
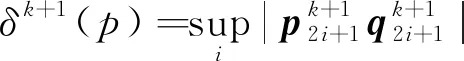
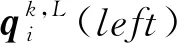
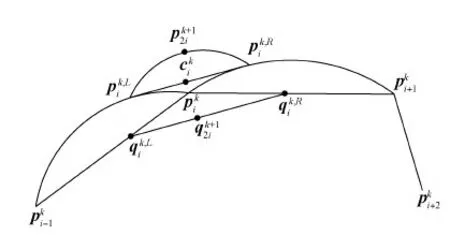
图3 本文的双参数4点binary细分法偏移步中新点与对应线性细分的新点之间的距离

由三角不等式，得

(17)

由Lipovetsky和Dyn(2019)中引理3.2，得

由Zhang等人(2020)中引理4，得

(18)

(19)

将式(12)和式(16)代入式(18)，得

(20)

将式(19)和式(20)代入式(17)，有

又由式(12)和式(16)，可知

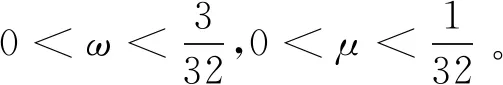
(21)

由于当张力参数ω以及偏移参数μ满足max{4|μ+2ω|,4ω+|1-4μ-4ω|}<1时，线性双参数binary 4点细分C1连续，因此本文提出的细分法是C1连续的。证毕。

2.4 数值图例

图4—图6为基于圆平均的双参数4点binary细分法的数值图例。张力参数ω刻画的是新点靠近控制多边形边的程度。ω越小，生成的极限曲线越接近初始控制多边形，如图4所示。偏移参数μ刻画的是细分过程中第k+1层的新点偏移第k层控制点的程度。μ越小，生成的极限曲线越接近初始控制顶点，如图5所示。这也充分体现了李彩云等人(2019)的方法是本文基于圆平均的双参数4点binary细分法的特例，当位移参数μ=0时，本文方法即为李彩云等人(2019)提出的基于圆平均4点插值细分法。由于该细分法在细分过程中新点的位置与法向量有关，所以初始控制顶点不同的法向量也会影响极限曲线，如图6所示，在初始控制顶点相同，改变其中一个控制顶点的法向量的情况下，在初始控制顶点的法向量与相邻2个控制顶点的法向量相比均变化很大时，极限曲线出现了自交的情况。因此，选择合适的法向量可以避免产生的极限曲线。

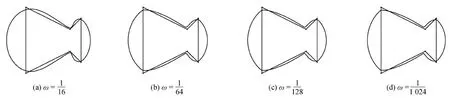
图4 不同张力参数下的基于圆平均的双参数4点binary细分法的极限曲线

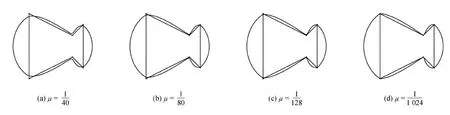
图5 不同偏移参数下的基于圆平均的双参数4点binary细分法的极限曲线

图6 不同初始点法向量对基于圆平均的双参数4点binary细分法极限曲线的影响

3 基于圆平均的单参数3点ternary插值细分法

3.1 本文的3点细分法

线性单参数3点ternary插值细分法的细分规则为

(22)

式中，ω为形状参数，细分进程如图7所示。

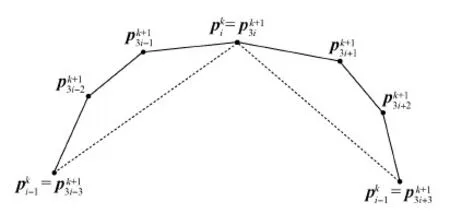
图7 线性单参数3点ternary细分法的细分过程

可以看出，每次细分过程均由一个左插步、一个右插步和一个插值步组成。当1/6<ω<1/3，线性单参数3点ternary细分法是收敛的(Zheng，2003)。式(22)可改写为

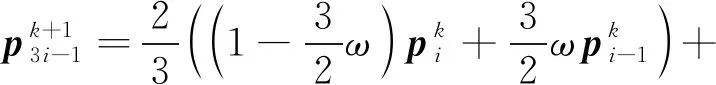
(23)

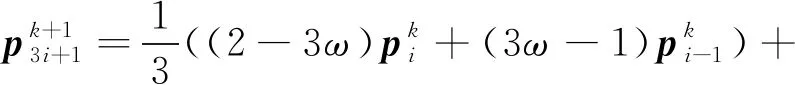
(24)

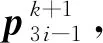
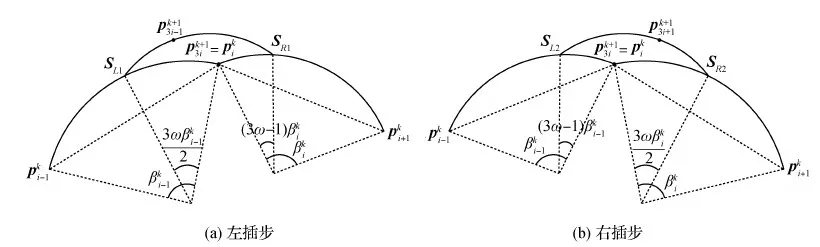
图8 本文单参数3点ternary细分法的构造

算法2 基于圆平均的单参数3点ternary细分法

输入：初始控制点及其法向量Pi=(pi,ni),i∈Z。

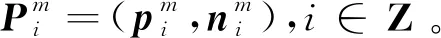
2)对于k=0,1,2,…,m;

执行∀i∈Z;

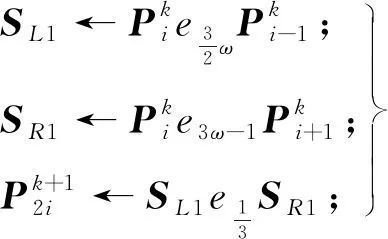
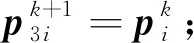
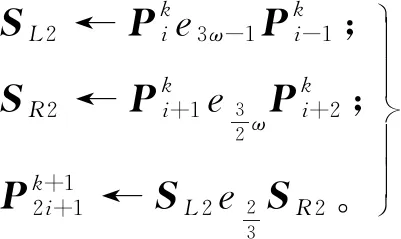
3.2 收敛性

证明：对于该细分法法向量的收敛性的证明可参考Dyn和Sharon(2017)与本文引理3的证明，不再给出详细证明。下面给出该细分法点的收敛性证明。

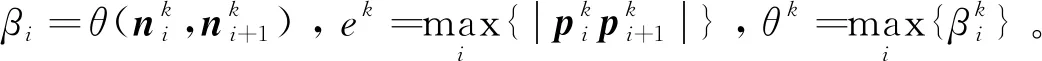
由三角不等式，得

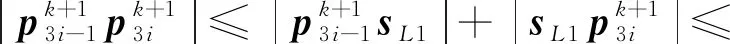
(25)

利用三角不等式对|sL1sR1|进行估计，有

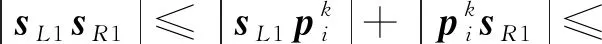
(26)

对θ(sL1,sR1)进行估计，有

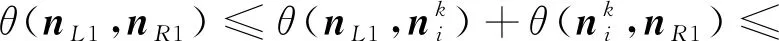
(27)

由式(25)—(27)，得

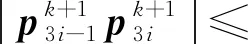
因此，ek+1≤ηkek。其中，

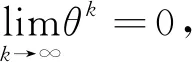
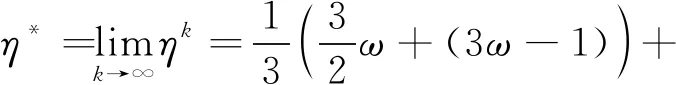
(28)

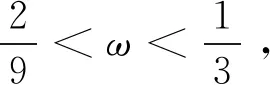
综上所述，本文的基于圆平均的单参数3点ternary插值细分法是收敛的。证毕。

3.3 连续性

定理4 当形状参数满足2/9<ω<1/3时，基于圆平均的单参数3点ternary细分法是C1连续的。

证明：与定理2证明过程类似。线性单参数3点ternary细分法的每次细分中，左插步和右插步均可以看做由两个内插步和一个平均步组成，如图8所示。

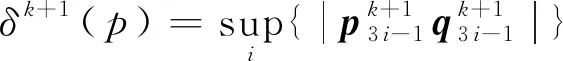
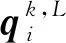
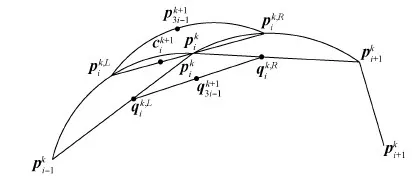
图9 本文的单参数3点ternary细分法左插步中新点与对应线性细分的新点之间的距离

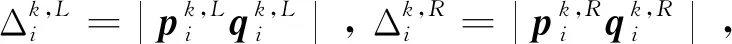
(29)

由Lipovetsky和Dyn(2019)引理3.2，得

再由引理5，得

(30)

(31)

(32)

将式(26)和式(27)代入式(30)，得

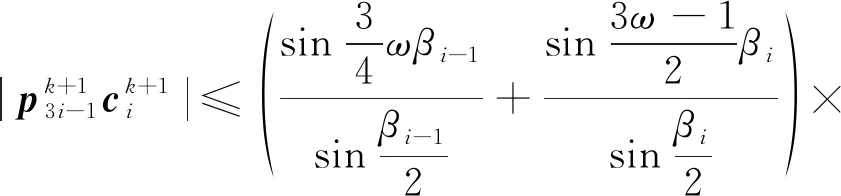
(33)

由式(29)—(33)，有

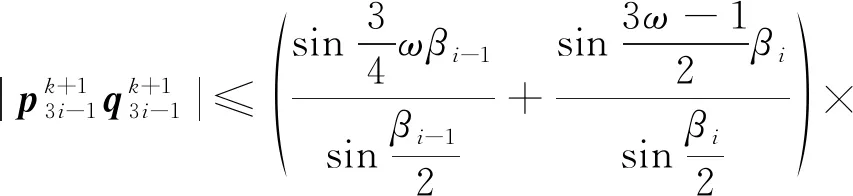
(34)

由式(27)和式(28)可知

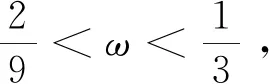
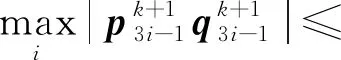
(35)

3.4 实验与比较

图10是基于圆平均的单参数3点ternary插值细分实例。如图10所示，当形状参数ω分别取0.25，0.275，0.3，0.32时，基于圆平均的单参数3点ternary插值细分生成的极限曲线也不同。该细分法与初始控制顶点的法向量有关，如图11所示，初始控制顶点相同，改变其中一个控制顶点的法向量，会出现自交情况，所以选择合适的法向量可以避免产生极限曲线自交。

图10 不同参数ω下的基于圆平均的单参数3点ternary插值细分极限曲线

图11 初始点的法向量对基于圆平均的单参数3点ternary插值细分极限曲线的影响(ω=0.325)

实验将线性双参数4点binary细分法与线性单参数3点ternary插值细分法作为线性细分方案1和线性细分方案2与本文的两种细分法进行比较。结果表明，本文的细分法具有圆再生力，且生成的极限曲线与传统方法相比更光滑。

如图12所示，当初始控制顶点从圆采样，对应的法向量为从圆心到顶点指向圆外。方案1与方案2细分产生的极限曲线都不能重现圆，而基于圆平均的双参数4点binary细分法与基于圆平均的单参数3点ternary插值细分均能再生圆。

本文提出的基于圆平均的4点细分与3点细分的造型能力均比对应的线性细分方法好。实验选取3个曲线模型实例进行不同细分法的曲线重建比较。3个实例均是从连续曲线上采样获得的初始控制点及其法向量，生成的曲线均是细分8次所得。图13是例1凹形曲线模型的重建，其中，图13(a)是初始采样点及其法向量，图13(b)—(e)分别是线性双参数4点binary细分法、本文的4点细分法、线性单参数3点ternary插值细分法与本文的3点插值细分法。图14是例2的曲线模型重建比较，图15是例3手型曲线模型的重建比较，各子图含义同图12。从图13—图15可以看出，方案1、方案2和本文方法均能重建曲线，但方案1和方案2生成的曲线都有尖锐点，而本文的4点细分和3点细分法生成的曲线都比较光滑，特别是例3，初始控制点与法向量杂乱无章，但用本文方法生成的曲线可更好地重现一张光滑手的形状。

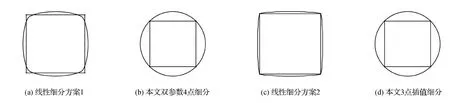
图12 不同细分方法的圆的再生力比较

图13 例1曲线模型

图14 例2曲线模型

图15 例3曲线模型

4 结 论

本文针对带法向约束的离散点集重建问题，提出基于圆平均的双参数4点binary细分和单参数3点ternary插值细分两种非线性细分法，利用引理1与引理2 证明了本文两种细分法的收敛性与C1连续性。对基于圆平均的双参数4点binary细分，当偏移参数μ=0时，可以实现插值。这也是李彩云等人(2019)提出的基于圆平均的带参数4点插值细分的推广。对基于圆平均的3点ternary插值细分，在实现插值的同时，每次细分获得的控制顶点是上一次控制顶点的3倍，这使得细分过程中控制顶点的增加速度更快。本文的两种方法与对应的线性细分法相比，本文方法可以得到更加光滑的曲线，图像编辑能力强，且具有圆的再生力，克服了线性细分法容易产生尖锐点、难生成圆的问题。对从3个封闭连续曲线实例上采样获得的初始控制点及其法向量的数据集，均可以很好地重建。理论证明与数值实验表明，本文方法可以较好地解决带法向约束的离散点集的曲线重建问题。

但是，本文方法仍存在不足之处。当离散点集的法向量发生突变时，生成的曲线往往会自交，因此需要选择合适的法向量避免极限曲线自交。此外，本文方法的参数满足什么样的范围可达到C2连续与C3连续以及将本文方法推广到曲面，值得进一步探究。