基于拓扑绝缘体纳米线约瑟夫森结的反常临界超流增强和半整数夏皮洛台阶

侯延亮 王翔 孙晓培 吕力3)†

1)(中国科学院物理研究所,北京凝聚态物理国家实验室,北京 100190)

2)(中国科学院大学物理科学学院,北京 100049)

3)(松山湖材料实验室,东莞 523808)

基于拓扑绝缘体材料的约瑟夫森结是寻找马约拉纳零能模的候选器件,因而受到拓扑量子计算研究领域的关注.这方面实验的关键之一,是制备具有优质结区的约瑟夫森器件.本工作在三维拓扑绝缘体Bi2Te3和Bi2(SexTe1–x)3 纳米线上制作了约瑟夫森结器件,研究了其结区的超导邻近效应、多重安德列夫反射和超流-相位关系,观测到了约瑟夫森结的临界超流随磁场增大而反常地增大、其交流约瑟夫森效应出现半整数的夏皮洛台阶的实验结果.本文还讨论了这些反常现象的可能来源,特别是与结区界面处超导电极的Ti 缓冲层和拓扑绝缘体纳米线中的Te 元素形成TiTe 铁磁性合金层的关系.

1 引言

2008 年,Fu 和Kane[1]从理论上提出,拓扑绝缘体表面态在s 波超导体的邻近效应诱导下,能够表现出类p 波超导电性,从而产生满足非阿贝尔统计的马约拉纳零能模.这一想法一经提出,引起了科研工作者的广泛兴趣.马约拉纳零能模受拓扑保护,对外界干扰免疫,可以大大提高量子态的退相干时间,为量子计算的实现提供了新的思路.基于拓扑绝缘体的超导邻近效应设计、制备可行的拓扑量子器件,寻找并验证马约拉纳零能模的存在,可以为下一步实现拓扑量子比特及其编织操作打下实验基础,具有重要的意义.

为了制备出高质量的约瑟夫森器件,需要解决两个方面的问题:一是选用高质量的拓扑绝缘体材料,二是控制好超导电极与拓扑绝缘体的界面.在材料质量方面,现有拓扑绝缘体材料的一大问题是体态的导电成分占比较大,导致表面态信号较弱.解决的方法是生长多元的材料,并对成分进行调控,通过改变费米面的位置而提高表面态的占比[2−5].常用的生长拓扑绝缘体纳米材料的方法有分子束外延生长法[6,7]、气-液-固化学气相沉积生长法[8,9]、马弗炉生长法[10,11]等.目前已生长出了不同元素组分的拓扑绝缘体材料,在此基础上制作的约瑟夫森结器件,其结区的透射系数高达0.85[12,13].在电极材料与拓扑绝缘体界面的控制方面,选择合适的电极材料可以有效避免出现复杂的界面情况.例如,如果选择Pd 膜作为超导电极与含Te 拓扑绝缘体之间的缓冲层,在界面处会生成PdTe 和PdTe2超导合金相,从而增加了系统的复杂度[14−17].

本工作构筑了基于三维拓扑缘体纳米线的约瑟夫森结器件,观测到了两个反常的实验现象:1)临界超流随外加磁场的增强而反常增大;2)在交流约瑟夫森效应中出现半整数夏皮洛台阶.为了探寻其背后的物理机理,对器件界面进行透射电子显微镜(transmission electron microscope,TEM)观察、能谱表征分析以及磁矩测量等.实验结果表明,器件界面处形成了有别于电极缓冲层材料Ti 和纳米线的铁磁性TiTe 合金层.通过讨论这一铁磁性合金层与所观察到的反常现象的关系,认为铁磁性的引入破坏了约瑟夫森结系统的时间反演对称性,使其超流-相位关系(current-phase relation,CPR)不同寻常,由此可能导致了临界超流随磁场增强而反常增大的行为;并且,由于铁磁性的引入,结区形成了超导-铁磁金属-超导(superconductorferromagnetic metal-superconductor,SFS)结和超导-正常金属-超导(superconductor-normal metalsuperconductor,SNS)结的混合系统,使得存在π 周期的CPR,导致半整数夏皮洛台阶的出现.目前,还没有关于器件界面效应引起类似反常现象的报道和讨论.本文工作将有助于下一步改善器件界面、从而制备出基于拓扑绝缘体纳米线的高质量拓扑量子器件.

2 实验

2.1 材料生长

采用三温区的化学气相沉积管式炉,以气-液-固生长机制的原理,在不同温度的硅基片上长出了不同组分的三维拓扑绝缘体纳米线材料.实验过程中,首先将Bi,Se,Te 等单质粉末源料放置于管式炉第一温区的中央区域,再将准备好的表面附有离散分布金颗粒的10 片5 mm×5 mm 硅基片,按顺序排布放置于管式炉第二、三温区之间的过渡区域;其次,密封管路,向炉内通入比例为4∶1 的氩气和氢气,维持炉内气体氛围压强在100 mbar(1 bar=105Pa);然后,设置升温程序,使3 个温区最终的温度分别为580 ℃,580 ℃,380 ℃,在基片上沉积材料40 min 后,将管式炉降温至室温,取出带有样品的基片;最后,对生长出的材料进行扫描电子显微镜(scanning electron microscope,SEM)形貌观察和能谱分析(energy dispersive spectroscopy,EDS)等.结果表明,长出的材料为三维Bi2Te3纳米线、Bi2(SexTe1–x)3纳米线等,纳米线的长度处于5—10 µm 范围内,宽度处于20—300 nm范围内.

2.2 器件制作

首先,挑选合适的三维拓扑绝缘体纳米线,将其转移到表面附有300nm厚SiO2层的硅基片上;其次,以4000rad/min的速率在基片上旋涂950PMMA A4 胶,并用加热台将其在120 ℃下加热2 min 使胶固化;然后,利用电子束曝光的方法在样品上实现微纳加工图形设计,经显影、定影等步骤后,分别在Ar/O2和Ar 环境下各离子束刻蚀40 s,以去除曝光区域的残胶;最后,再用高真空的PLASSYS 镀膜设备在基片上蒸镀Ti/Al 薄膜(3/80 nm)后,取出样品,将其泡在丙酮溶液中完成去胶操作.至此,完成了多个基于三维拓扑绝缘体纳米线的约瑟夫森结器件的制作.器件设计的结区间距在50—200 nm 范围内.

2.3 器件测量

将制备好的约瑟夫森结器件放置于环境温度为20 mK 的干式稀释制冷机系统中进行测量.测量系统主要包括滤波和接地系统、吉时利(Keithley)源表和锁相放大器等数据采集系统、微波传输系统等.其中,滤波系统为三级滤波,包括RC 滤波、π 型滤波、铜粉滤波等;采用Keithley 2400 源表对超导磁体施加电流来实现外加磁场的精确控制,用LI5640 锁相放大器采集约瑟夫森结器件的微分电阻信号,测量约瑟夫森结器件临界超流随磁场的变化;用斯坦福SG384 射频信号发生器通过微波传输线在约瑟夫森结器件附近施加微波辐射场,测量约瑟夫森结的交流约瑟夫森效应.

3 结果和讨论

3.1 临界超流反常增大行为和半整数夏皮洛台阶现象

首先,对器件表面施加了垂直磁场,测量了结区临界超流随磁场变化的关系.图1(a)和图1(b)中的SEM 图分别对应基于三维拓扑绝缘体Bi2(SexTe1–x)3纳米线和Bi2Te3纳米线的约瑟夫森结器件实物图.通过对这两个器件进行测量,观测到临界超流随磁场增强而反常增大的现象,如图1(a)和图1(b)中的数据图所示.为了验证实验现象的重复性和可靠性,测量了另外5 个基于拓扑绝缘体纳米线的约瑟夫森结器件,同样观测到了这样的反常实验现象.

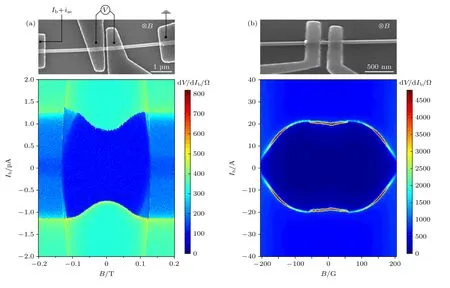
图1 (a),(b)分别为基于Bi2(SexTe1–x)3 纳米线和Bi2Te3 纳米线约瑟夫森结器件的SEM 图,以及各自对应的微分电阻随偏置电流和磁场而变化的实验数据,其中Ib 为直流偏置电流,iac 为低频交流电流,V 为结区电压,B 为施加的磁场Fig.1.(a)and(b)Scanning electron microscope images of two Josephson junction devices based on Bi2(SexTe1–x)3 nanowire and Bi2Te3 nanowire,respectively,together with their differential resistance as a function of bias current and magnetic field.Ib,iac,V andB represent dc bias current,low-frequency ac current,voltage drop across the junction,and applied magnetic field,respectively.

随后,又测量了图1(b)中的器件在微波辐射下的交流约瑟夫森效应,希望得到该约瑟夫森结超流-相位关系方面的信息.图2(a)和图2(b)分别为0 G 和100 G(1 G=10–4T)垂直磁场下的微分电阻随微波功率和偏置电流变化的实验数据.微波频率为3.33GHz,微波功率从–60dBm增至–20dBm.实验数据呈现出交流约瑟夫森效应和夏皮洛台阶.白色数字标注的深蓝色区域是整数夏皮洛台阶出现的区域.除了整数夏皮洛台阶之外,还观测到了半整数的夏皮洛台阶,如红色箭头所标示.图2(c)和图2(d)分别为图2(a)和(b)局部的放大图,与0 G 垂直磁场下的半整数的夏皮洛台阶相比,100 G垂直磁场下n=±1/2,±3/2 的半整数台阶更清晰,同时还出现了n=±5/2 的半整数台阶.图2(e)为图2(a)图中几个不同微波功率处的微分电阻随偏置电压的变化关系曲线,红色箭头标记的是半整数台阶出现的位置,蓝色箭头标记的是整数台阶出现的位置,台阶对应的偏置电压位置V(n)和台阶序号n很好地符合了V(n)nhf/2e的关系,其中h为普朗克常量,f为给约瑟夫森结施加微波的频率,e为电子电荷.

图2 图1(b)中的器件在微波辐射下出现整数和半整数的夏皮洛台阶(a),(b)分别为0 G 和100 G 垂直磁场下的微分电阻随微波功率和偏置电流而变化的实验数据,白色数字标示的深蓝色区是对应序号的整数台阶出现的区域,红色箭头标示的是半整数台阶出现的位置;(c),(d)是(a),(b)局部的放大图,展示在100 G 的垂直磁场下,半整数台阶比零磁场下更为清晰;(e)图(a)中几个不同微波功率处的微分电阻随偏置电压的变化关系曲线,红色箭头标记的是半整数台阶出现的位置,蓝色箭头标记的是整数台阶出现的位置Fig.2.Integer and half-integer Shapiro steps under microwave irradiation for the device shown in Fig.1(b):(a),(b)The differential resistance as a function of microwave power and bias current under the perpendicular magnetic field of 0 G and 100 G,respectively,showing Shapiro steps.Integer steps appear in the dark blue regions indicated by the white numbers.And,half-integer steps appear in the positions indicated by the red arrows.(c),(d)Details of(a)and(b),showing that the half-integer steps can be more clearly seen in a perpendicular magnetic field of 100 G than in zero field.(e)Line-cuts in panel(a)at several different microwave powers and converted to bias voltage.Integer and half-integer Shapiro steps are marked with blue and red arrows,respectively.

3.2 讨论3.2.1 多重安德列夫反射和器件基本参数

接下来讨论出现临界超流反常增大和半整数夏皮洛台阶两个实验现象的原因.首先分析器件的一些基本参数,包括过量电流(excess current,Ie)、结区诱导的能隙大小Δ′、界面透射系数t等.

以图1(b)中Bi2Te3纳米线约瑟夫森结器件为例,测量得到了如图3(a)所示的Ib-V曲线.当约瑟夫森结处于大偏置下的正常电阻态时,将此位置的曲线沿其切线方向延长,得到与纵轴相交的截距为50 nA,即为过量电流Ie.另外,该约瑟夫森结在大偏置下的正常态微分电阻Rn为1300 Ω,其临界超流值Ic为20 nA,由此可知该器件的eIcRn=26 µeV.

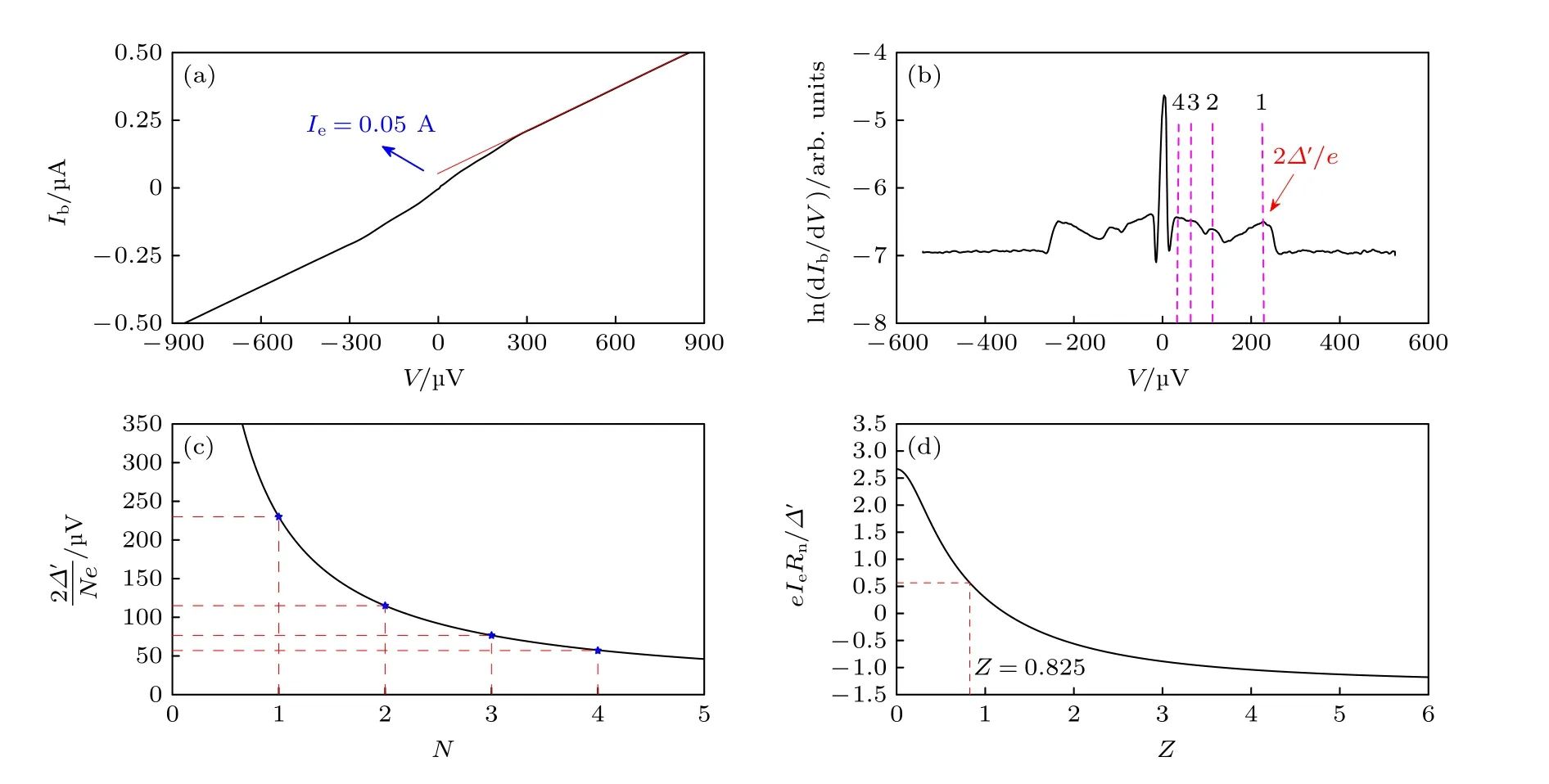
图3 多重安德列夫反射(a)基于图1(b)约瑟夫森结器件的Ib-V 曲线,过量电流为50 nA;(b)多重安德列夫反射导致的电导峰;(c)电压峰的电压位置与电导峰的序号符合理论预计;(d)根据OTBK 理论得出的eIeRn/Δ′ -Z 的曲线[18]Fig.3.Multiple Andreev reflection:(a)TheIb-V curve of the Josephson junction device shown in Fig.1(b),the excess currentIe is 50 nA;(b)the conductance peaks caused by multiple Andreev reflections;(c)the peak positions follow the expectation of the theory;(d)theeIeRn/Δ′ -Z curve derived from OTBK theory[18].

图3(b)为其多重安德列夫反射(multiple Andreev reflection,MAR)数据图,MAR 出现在电导峰对应的偏置电压位置.可观测到的MAR 的阶数有四阶,如图中N=1,2,3,4 序号标注所示.发生一阶MAR 时对应的结区偏置电压位置为2Δ′/e=230 µV,即诱导的超导能隙Δ′为115 µeV.如图3(c)所示,发生MAR 时对应的结区偏置电压值和阶数能够很好地与MAR 的理论公式(1)吻合:

根据Octavi-Tinkham-Blonder-Klapwijk(OTBK)理论可以得到结区界面的势垒强度Z、诱导的能隙Δ′、过量电流Ie、正常态电阻Rn之间的关系,即[18]:

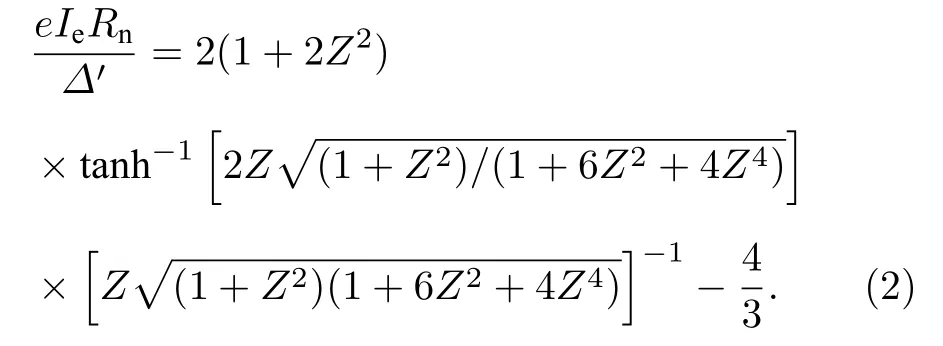
其关系曲线图展示在图3(d)中.根据前面已知的参数Ie=50 nA,Rn=1300 Ω,Δ′=115 µeV,可知eIeRn/Δ′=0.525.那么,根据图3(d)可得到结区界面的势垒Z为0.825,如图中的红色虚线标注所示.由此得到器件界面的透射系数t1/(1+Z2)=0.595.

根据以往以Al/Pt 作为超导电极的Bi2Te3和Bi2Se3约瑟夫森器件的研究报道,eIcRn可达到Al 超导能隙的60%以上,界面的透射系数可高达0.85[12,13].而在本文的多个器件中,eIcRn不到Al超导能隙的20%,界面透射系数也比较低(0.55—0.65).这从侧面表明本文器件界面有可能比较复杂,实验中出现的反常现象也可能与此有关.

3.2.2 器件界面效应:铁磁性的TiTe

为了探究器件界面的复杂情况是否与发生的反常现象有关,对器件进行TEM 观察、能谱分析以及磁矩测量等.实验结果表明,器件界面处形成了有别于电极缓冲层材料Ti 和纳米线的铁磁性TiTe 合金层.

图4(a)为基于三维Bi2Te3纳米线约瑟夫森器件的结区截面TEM 图以及能谱分析.元素成分分析表明,在结区界面处黄色虚线标示的范围内Ti 元素和Bi 元素重叠很少,而Ti 和Te 元素重叠较多.因此,可以确定在此区域内形成了Ti 和Te的合金.

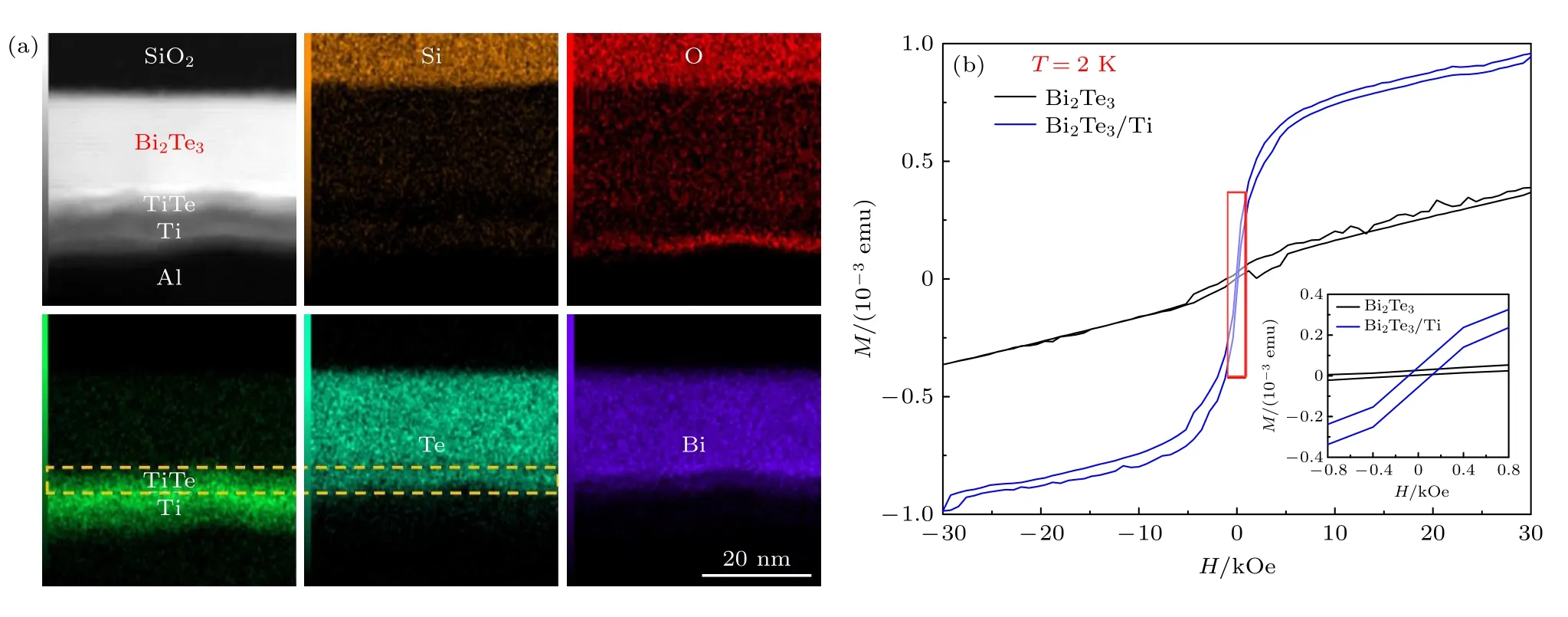
图4 (a)基于三维Bi2Te3 纳米线约瑟夫森器件截面的TEM 图以及能谱分析的元素成分面扫描图,Bi2Te3 与电极缓冲层Ti 的界面处产生了TiTe 合金层,位置如图中黄色虚线框所示;(b)Bi2Te3 薄片样品和蒸镀Ti 后的Bi2Te3/Ti 异质结样品在2 K 温度下的M-H 曲线数据图(1 emu=10–3 A·m2),插图为红色方框区域实验数据放大图Fig.4.(a)Transmission electron microscope image on the cross-section of the Josephson junction device composed of a three-dimensional topological insulator nanowire Bi2Te3 and superconducting electrodes with buffer layer Ti at the interface.Also shown are the elemental mappings at the interface by energy dispersive spectroscopy.The two dashed yellow lines indicate where TiTe alloy is formed at the interface;(b)theM-H curves measured at the temperature of 2 K on a Bi2Te3 flake before and after Ti film deposition,the inset shows the enlarged details in the red box.

有研究报道,单层或几层的TiTe 材料为铁磁性的狄拉克半金属,Ti 原子层和Te 原子层间会存在鲁棒性的铁磁序交换耦合机制,使得TiTe 具有强铁磁性[19].为了判断器件界面处的Ti 和Te 合金相是否是TiTe 合金相、是否具有铁磁性,在Bi2Te3薄片(厚度为30 nm)上蒸镀Ti 膜(厚度为3 nm)之前和之后的样品上,分别测量2 K 温度下的M-H曲线,结果如图4(b)所示.与蒸镀Ti 前的结果相比,蒸镀Ti 后的Bi2Te3/Ti 异质结样品的M -H曲线在2 K 的低温下呈现出了铁磁性回滞,矫顽力在100 Oe(1 Oe=103/(4π)A/m)左右,说明Bi2Te3/Ti 异质结样品具有铁磁性磁矩.因为Bi2Te3和Ti 膜本身都不具有铁磁性,所以可认为,在器件界面处,电极的缓冲层Ti 膜与拓扑绝缘体材料的Te 元素发生了化学反应,生成了具有铁磁性的TiTe 合金层.铁磁性TiTe 层的出现,为揭示两个反常实验现象的物理机理提供了重要线索.

据报道,基于InAs、石墨烯的约瑟夫森器件可以形成高透射系数的结区和重倾斜的CPR,使得CPR 出现高阶谐波,导致微波辐照下整数和半整数夏皮洛台阶的出现[20,21].而本文器件具有较低的界面透射系数t=0.595,其CPR 更接近于正弦函数,因此可以排除本实验中半整数夏皮洛台阶的出现是由重倾斜CPR 导致的.另外,库珀对中电子塞曼分裂导致的Fulde-Ferrell-Larkin-Ovchinnikov(FFLO)超导态[22,23]产生非零动量的超导配对机制,形成空间分布的p 波,亦有可能导致本实验中反常现象出现,但目前尚未有足够的实验证据验证.

另一方面,在基于SnTe,NiFe 等的约瑟夫森器件上,也观察到了临界超流随磁场增强而反常增大的行为和交流约瑟夫森效应中出现半整数夏皮洛台阶的行为[24,25],基于此,结合本实验的具体情况,对所观察到的反常现象给出如下可能的物理机理解释.

有研究认为,时间反演对称性破缺可导致出现临界超流随磁场增强而反常增大的行为[24].在本文器件的界面处形成了铁磁性的TiTe 合金,铁磁性的引入打破了系统的时间反演对称性,从而导致了临界超流随磁场增强而反常增大的行为.

另有研究报道,在SFS 结和SNS 结混合的Nb-NiFe-Nb 约瑟夫森结中存在着0 结和π 结的竞争机制,使得CPR 中含有π 周期的二阶谐波相,导致在交流约瑟夫森效应中出现了半整数的夏皮洛台阶[25].在本文的器件中,界面处产生了铁磁性的TiTe 合金层,同样可能使得结区形成SFS 结和SNS 结的混合系统,导致CPR 中也含有π 周期的二阶谐波相,因此在微波辐射下的交流约瑟夫森效应中出现了半整数的夏皮洛台阶.另外,与0 G的情况相比,100 G 垂直磁场下出现了更高阶和更清晰的半整数夏皮洛台阶(图2).这可能与在100 G下TiTe 铁磁性更强有关.

4 总结

综上所述,约瑟夫森器件中电极缓冲层Ti 膜与拓扑绝缘体的Te 元素化合形成了具有铁磁性的TiTe 合金.铁磁性TiTe 层的出现,不仅打破了系统的时间反演对称性,导致出现临界超流随磁场增强而反常增大的行为,同时还使得结区构成了SFS 结和SNS 结的混合系统,致使CPR 含有π 周期的二阶谐波相,在交流约瑟夫森效应中出现半整数的夏皮洛台阶.本文基于拓扑绝缘体纳米线的约瑟夫森器件,首次观察到可能由器件界面效应引起的类似反常现象,这为以后改善结区界面,制备出高质量可行的拓扑量子器件做了良好的铺垫,也为后续在拓扑量子计算领域中研究马约拉纳零能模打下实验基础.