紧凑式离轴三反光学系统设计

蒋成斌，陈智利，王肖同，张 媛，成姗姗

西安工业大学 光电工程学院，陕西 西安 710021

1 引言

离轴反射系统因其无色差、无中心遮挡和紧凑结构等特点，在现代空间光学遥感领域广泛应用于对地遥感观测[1-2]和星载激光雷达探测[3-4]等场景。特别是离轴三反光学系统在满足高像质和轻量化设计需求方面具有明显优势，相较于离轴两反和离轴四反系统更具潜力[5]。随着空间遥感技术的不断发展，关于离轴三反光学系统的分辨率、工作波段和紧凑性的要求也随之不断提高，以便满足高分辨、宽光谱和轻小型的设计目标。

随着技术的发展，离轴三反光学系统在空间光学领域得到广泛应用和认可。参考文献[6]设计了一款多谱段推扫式的离轴三反光学系统，工作波段为0.47 μm 至0.87 μm，有效口径为20 mm，视场达到36°×6°，在轨道高度为600 km，地面像元分辨率GSD 为50 m。整体结构为主镜、三镜使用高次非球面，次镜使用二次曲面，在奈奎斯特频率71 lp/mm处MTF 值大于0.6，成像质量良好。参考文献[7]设计的大视场推扫式光学系统在非球面三反系统的基础上，对主镜和三镜采用了Zernike 自由曲面，分析了不同项对像差的影响，最终设计的离轴三反系统焦距为1300 mm，视场为35°×2°，在轨道高度为650 km，地面像元分辨率为4.4 m，系统在50 lp/mm 处MTF大于0.5，最大畸变为2.9%。参考文献[8]设计的星载高分辨率红外双谱段遥感器光学系统，在轨道高度为500 km，地面像元分辨率达到了5 m，相对孔径1/4，视场角2.3°，在空间频率25 lp/mm 处MTF 大于0.32，其视场角较小，成像范围有限。参考文献[9]设计了一款大视场离轴三反光学系统，其视场角为10°，相对孔径1/4.5，系统在轨道高度为400 km，地面像元分辨率为4 m，在71.4 lp/mm 处各视场MTF 均大于0.28，畸变小于0.1%。虽然离轴三反光学系统已得到普遍应用，但在现代空间光学领域的快速发展下，其系统结构、分辨率和工作波段的要求也在不断提升，而紧凑式离轴三反系统能够有效地压缩系统体积，从而节省材料和降低成本，并实现系统性能的提升。参考文献[6-9]所设计的系统成像质量都基本满足需求，但其结构仍不够紧凑，不能满足空间光学系统的尺寸小型化要求，且分辨率普遍不高，因此需要对紧凑式系统结构进行深入研究。

本研究旨在实现离轴三反光学系统结构的紧凑化并提高系统的分辨率，以满足空间光学轻小型的要求并获取细节更为丰富的图像数据，为各种遥感应用提供更精确的信息服务。通过对系统进行优化，实现可见光及近/中红外波段的高性能光学成像，有助于提高遥感图像的信息量，为地球观测和资源调查等领域提供更全面的数据支持[10]。可见光波段可用于地形检测、泥沙检测、植被检测、海洋监测等领域，近红外波段可应用于大气校正等领域[11]。针对空间遥感领域的特殊需求，本研究将致力于实现轻量化和紧凑性的优化设计，实现一种近圆形布局的离轴三反结构，以降低系统的质量和体积，为星载激光雷达探测等应用提供更为实用的解决方案。

2 指标需求分析

2.1 指标确定

本文设计的紧凑式离轴系统的指整体指标要求分别为：系统有效焦距800 mm，F 数为4，在400 km轨道高度上，可见光、近红外和中红外的地元分辨率分别为1.5 m、2.5 m、8.5 m。离轴三反系统的设计指标，包括入瞳直径、工作视场大小、探测器像元尺寸和奈奎斯特频率可由下列公式给出：

其中：D为光学系统入瞳直径，f为光学系统有效焦距，TFOV为光学系统的视场角，W为横向/纵向幅宽，H为卫星在轨高度，s表示像元大小，d为地元分辨率，φ表示像素的尺寸。

根据式(1)～(3)计算可得到本文设计的紧凑式离轴三反系统的具体设计指标如表1 所示。

2.2 系统方案选择

常见的光学系统有折射式、折反射式和全反射式系统三类[12]。全反射系统利用多个镜面来纠正光线的折射和散射，从而有效减少球差、彗差和像散等像差问题。这种设计方案可以提供更清晰、更准确的图像，同时提高望远镜的观测能力和性能。采用全反射系统还可以灵活地调整和优化光学参数，以满足特定的技术要求[13]。通过选择合适的镜面形状、曲率半径和镜面材料，可以实现更高的光学效率和更广泛的波段覆盖。

本设计采用全反射式非共轴结构(如非共轴孔径、非共轴视场等)，实现避免主镜与次镜之间的相互遮挡，以及三镜与次镜之间的相互遮挡。相对于共轴系统，非共轴系统不仅可以提供较大的视野，而且可以消除中间的遮挡。常见的离轴三反式光学系统设计有Cook 型三反系统，如图1 所示。它具有平坦的视场，其中二级和三级镜面呈球形，简化了制造[14]。这种布置的视野为7°×12°。由于该系统是共轴结构，三镜和主镜之间只存在口径上的偏心，而无倾斜，因此便于后期的装调工作。

图1 Cook 型三反系统Fig.1 Cook type three reverse system

而本文设计的紧凑型三反系统，其特点是三面反射镜的位置近似围成一个圆，像面位置位于第一面镜子和第二面镜子之间。直观的结构如图2 所示。此系统结合了孔径离轴和视场离轴的优点，既避免了中心遮挡，又实现了较大视场。在这种系统中，光线通过非中心孔径进入，并在非中心区域形成视场。这样的设计可以进一步优化系统性能，适用于对成像质量和视场要求较高的应用场景[15]。

图2 紧凑式结构示意图Fig.2 Compact structure diagram

3 紧凑型三反系统初始结构计算

在实际应用中，一般采用求解基础像差方程的方法来确定系统的初始构型。在此基础上，提出了一种利用视场角度离轴和XY坐标离轴的三反系统。随后，通过逐步增加视场优化来得到最终的结构。因此，一个良好的初始结构对于后续的优化过程起到至关重要的作用。

同轴三反系统的初始结构如图3 所示。

图3 同轴三反结构图[16]Fig.3 Triaxial structure diagram

根据图3，同轴三反光学系统的起始结构参数可以被确定，包括：一镜、二镜和三镜尺寸的半径R1、R2和R3；d1、d2作为所述主反射镜与所述辅助反射镜、所述辅助反射镜与所述第三反射镜的间距。得到了，这3 个二次曲线的系数，其中e表示偏心率。此外，还有 α1、α2、β1、β24 个相关参数。将这4 个相关参数引入到塞德尔像差公式中，可以得到一阶像差S1、S2、S3、S4的计算公式。取S1=S2=S3=0，可得三个非球面的非球面系数在消除了球差、像散、彗差的值，令S4=0可以消除场曲，最终得到四个轮廓参数的关系，通过高斯光学理论得R1、R2、R3、d1、d2。

为简化计算，取一二面厚度互为相反数，通过f′=−800 mm，α1=0.2，α2=1.8，可得到一组初始结构参数，如表2 所示。

表2 初始结构参数Table 2 Initial structure parameter

理想结构的初始离轴倾角计算公式为[17]

图4 理想结构示意图Fig.4 Ideal structure diagram

第一步根据系统参数f、R和dbf确定路径配置。结构可由上述6 个构造参数di和 θi描 述。焦距f和系统大小设置为800，即f=2R=800，需要的F 数为4，由图5 可得dbf/f=2，dbf可设置为1600，同时可知θ2的大小为1 35°。根据定义，d1=2αR=800。其他的构造参数d2、d3、θ1和 θ3即可通过式(5)～(8)计算得到，最终得到的初始参数如表3 所示。

图5 dbf/f 与部分参数的关系[17]Fig.5 Relationship between dbf/f and some parameters

表3 初始结构的倾斜和偏心Table 3 Tilt and eccentricity of the initial structure

4 系统优化与分析评价

首先是最基础的系统参数控制，如EFFL、WFNO 等操作数，按照设计所需要求直接设置。通过COVA、ABLT 操作数来限制圆锥系数。并运用FCGT、FCGS、TRAY、SPHA 及相关数学操作数来控制像差。基于上述求出的同轴三反光学系统对其优化并进行离轴操作，利用点到直线的距离公式来调控三面反射镜之间的距离，使三面镜子近似抵在一个圆上，来确保光学系统总体结构符合提出紧凑型结构。具体过程为：首先通过读取物面(面1)上边缘点以及主镜(面3)上边缘点的yz坐标信息，来确定一条直线，利用直线的斜截式y=kx+b来计算斜率k和截距b，然后获取次镜(面5)下边缘点的yz坐标信息，将这些坐标视为点，最后根据式(9)来求出点到直线的距离。图6 为对该方法的直观解释，图中红线为控制的距离。

图6 距离控制示意图Fig.6 Range control diagram

利用此方法对次镜到像面和三镜连线的距离进行约束以控制光学结构和遮拦，并对三镜到主镜和次镜连线的距离进行控制，避免三镜过度靠近主镜，从而导致两镜体互相嵌入无法正常生产安装。并通过PMVA、ABGT、ABLT 操作数将离轴量控制在预想范围内。

在初期三反射镜的面型选择为偶次非球面，并设置了4、6 阶系数为变量进行优化，获得了焦距为800 mm、视场为10°×6°、入瞳直径为150 mm 的非球面光学系统，发现成像质量并不符合要求，在−5度到0 度的视场范围内，MTF 值较低，无法满足成像要求。此外，系统存在一定程度的遮拦，需要进一步进行优化。通过像质评价可以得知，系统的MTF均匀一致性较差，MTF 频率为100 lp/mm 时的最大值为0.527，最小值为0.07，平均值为0.364。系统的RMS 半径为6.213 μm，畸变在边缘视场最大，达到1.4%。整个10°×6°的视场范围内，系统未能满足成像要求。

考虑到如果只采用偶次非球面或二次型反射镜，则由于其可优化的自由度太少，很难满足高阶像差的校正要求和设计结构的要求以及系统分辨率的要求。因此为消除离轴反射系统中的离轴像差、倾斜角度、不对称高阶像差等问题，本设计采用了自由曲面的Zernike 多项式表征的非球面，应用于三反结构中。该方法是在原有结构的基础上，通过向抛物面、双曲面等曲面中加入高阶项，使其具有柔性可调性。从而实现对结构的灵活调整。通过采用这种表征方式，设计能够满足结构紧凑和高分辨率要求，同时有效地校正高阶像差。这样系统能够优化设计自由度，满足高分辨率要求，并有效校正离轴反射系统产生的高阶像差[18]。

Zernike 多项式[19]是一种在光学和图像处理中常用的函数，它在自由曲面设计中也有重要的应用。具体来说，Zernike 多项式的形式为

式中：N为Zernike 多项式的项数，Ai为第i项的系数，c为顶点的曲率，r为径向口径，ρ为极坐标半径，φ为极坐标角。

本文将一个Zernike 自由曲面引入到偶次非球面体系中。在此基础上，我们对Zernike 多项式的Z1-Z5 项目首先进行了优化，后续在系统无法达到理想成像效果的基础上每次增加5 项，然后逐步将X-轴向的视野扩展每一次0.1 度。同时，通过每次采取微小变化，避免因Zernike 系数变化而引起的评价函数和系统失效，从而避免引起系统的崩坏。在优化过程中，对反射镜的倾斜度、偏心度、视场的离轴角、RMS 半径进行了人工同步监测，从而保证了设计的准确性和合理性。经过反复优化最终得到自由曲面推扫光学系统焦距为800 mm、视场为12°×6°、入瞳直径为200 mm 和畸变小于1%的紧凑式离轴三反光学系统。结构示意图如图7 所示。

图7 最终设计系统结构图Fig.7 Final design system structure diagram

其中Zernike standard 自由曲面系数由表4 给出，可见光、近红外和中红外波段的MTF 图如图8、图9 和图10 所示。可见光、近红外和中红外波段的RMS 点列图如图11、图12 和图13 所示。通过像质评价可以得知，在可见光、近红外、中红外波段，系统的MTF 均匀一致性较好，可见光波段、近红外和中红外波段衍射MTF 值分别在截止频率为160 lp/mm、100 lp/mm 和30 lp/mm 时均大于0.2。系统的点列图的RMS 半径平均为2 μm。畸变在边缘视场最大，达到0.996%，如图14 所示，不超过指标要求的1%。整个12°×6°的视场范围内，该系统的成像质量良好，所设计的系统满足设计要求。

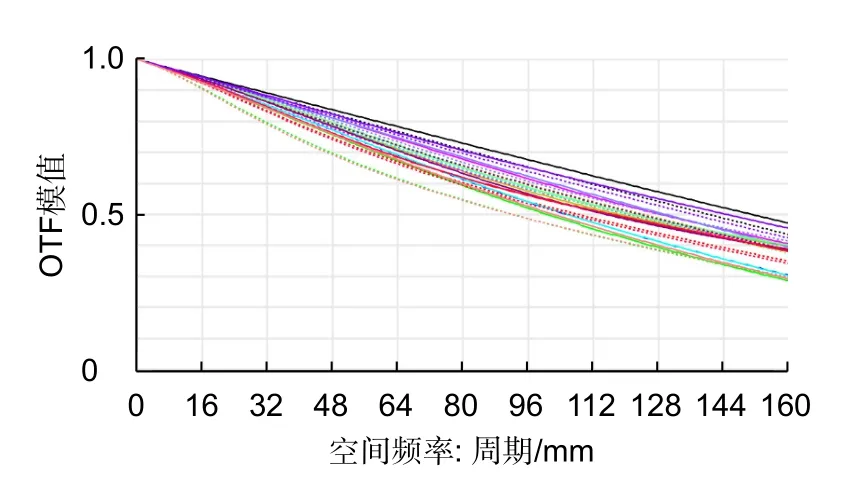
图8 系统可见光波段MTF 图Fig.8 MTF diagram of the system in visible band

图9 系统近红外波段MTF 图Fig.9 MTF diagram of near infrared band of the system

图10 系统中红外波段MTF 图Fig.10 MTF diagram of mid-infrared band of the system

图11 系统可见光波段点列图Fig.11 System visible light band point diagram

图12 系统近红外波段点列图Fig.12 System near infrared band point diagram

图13 系统中红外波段点列图Fig.13 System middle infrared band point diagram

图14 系统畸变图Fig.14 System distortion diagram

表4 Zernike standard 自由曲面系数表Table 4 Zernike standard free-form surface coefficient table

5 公差分析

曲面的形状误差主要包括光阑的直径容差、曲面的特定尺寸和参数容差、曲面的不平整容差。对于Zernike 自由曲面，需要单独考虑使用Zernike 的标准面不规则度，因此对于偶次非球面和自由曲面分析主要是利用PV 分析，使用TEXI 公差操作数独立地在非球面和自由曲面表面上随机产生矢高偏差峰值-谷值(PV)波动，为加工表面形状引入一种随机误差。利用ZEMAX 内置容限评定工具，并选择敏感性分析。以RMS 数值和MTF 数值作为判断准则，设定最大取样点数目20 个。在一定的上下容许范围内，采用蒙特卡罗算法，以正态分布为随机样本。在调试过程中，先把第三反射镜固定好，因为在离轴测试中第三反射镜的移动和倾斜是导致系统性能下降的主要原因，所以把它当作安装基准。表5 为公差分配表。

表5 误差分配表Table 5 Error distribution table

依据目前装配公差的实际情况，通常MTF 的降低一般是0.1 或者更少。基于RMS 半径的平均值和MTF 的平均值，进行容限分析。选取对系统有较大影响的10 个公差项目，对其进行模拟调试的困难程度及关键因素进行了分析。利用蒙特卡罗方法，通过累计叠加计算，获得了RMS 和MTF 累计统计概率。

其中，装调过程中倾斜度误差造成整个系统的性能降低最为明显，是导致整个系统性能降低的主要原因，所以必须对其进行严格的公差控制。为了获得预定的性能，在安装调试时需要严格把控移动和倾斜，对安装调试提出了挑战。此处给出了此设置下RMS半径和MTF 在150 lp/mm 的蒙特卡罗累计概率如表6所示。

表6 蒙特卡罗累计概率统计表Table 6 Monte Carlo cumulative probability statistic

6 结论

空间光学是基础科学的应用前沿。在现代遥感技术中，空间光学系统的分辨率与视场对于获取高质量的图像至关重要。本文利用近圆形的三反结构的构造，对视场进行了偏心和倾斜，提出了一种基于偶次非球面反射镜的设计方案。在此基础上，为增加成像质量，提出了一种基于Zernike 自由曲面的紧凑式离轴三反光学系统，并满足了长焦距、大视场和宽光谱的要求。最终所设计的系统为12°×6°，焦距为800 mm，像方F 数为4，视场角为12°×6°，畸变为0.996%，工作波段为0.486～0.656 μm 和0.78～2.5 μm 和3～5 μm，该系统点列图最小为1.6 μm，MTF 达到成像要求，能够在较大视场范围内，得到较佳的像质。