基于“数形结合”探索学生数学核心素养的形成

朱倩

【摘要】在数学学习中，数形结合是一个重要的数学思想，也是一种常用的数学方法.数学课堂需要在师生的互动中呈现“数形”的学习策略，让学生学会用“图形”来解题，见数拟形，见数思形，见数成形.文章通过例题切入，让学生在解题过程中树立“图形”意识，感受数形结合的好处，理解从“数形”到“塑型”的数学思想形成，培养学生的数学素养，从而使数学学习更具“数学味”.

【关键词】数形结合例题；数学素养

在小学数学教学中，若赋予数量关系、抽象概念和解析式几何意义，往往会使相关内容变得非常直观，若通过数量关系研究一些图形的属性，则会使图形的性质更丰富、更深刻.但是，在学习初学数学时，很多学生往往没有对“数”的含义进行深度思考，常常出现见数就用，从而做错题的现象.同时，很多老师也是就题讲题，忽略了学生数学素养的培养，没有合理运用策略.教师如果合理利用“数形”结合思想，并加以引导，学生很容易发现解题途径，并在操作中形成“模型”，这样就避免了复杂的计算与推理，简化了解题过程，更有助于学生形成好的解题习惯，使学生在练习中掌握知识和技能，在探究中获得经验，在实践中形成素养，使学生体验“获得”的快乐.

一、结合例题，引发思考

教师要经常鼓励学生从简单问题出发，积极引导思考，鼓励“学有疑”的学生走上讲台，大胆提问，把时间留给学生.评讲如下例题时，笔者更关注学生的主动思考.

例：一根木料锯成4段要12分钟，如果每锯一段所用的时间相同，那么锯成7段要花多少分钟？

对于平时就不爱动脑筋的学生，解这道题时，见数就用，很少动手操作去发现解法.而作为教师，一无锯二无木，如何生动形象、妙趣横生地讲给学生听呢？经过考虑，决定把题目出示在黑板上，看看学生有什么反应.

二、积极引导，解决问题

小学生思维发展的基本特点是由以具体形象思维为主要形式逐步过渡到以抽象逻辑思维为主要形式，但是这种抽象逻辑思维在很大的程度上仍然是直接与感性经验相联系的，仍然具有很大成分的具体形象性.在实际教学中，利用好的案例，积极鼓励学生参与操作，引发思考，有助于学生形成好的学习习惯，形成好的数学素养.

（一）初探：撕

例题一出，课堂由安静变得热闹起来，由无声到窃窃私语，再由私语渐变成激烈讨论.有两名同学争论得尤为激烈，一名同学左手拿着一张小纸条，右手高高扬起，好像在做“撕”或“切”的动作，另一名同学也是不甘示弱，喋喋不休，其他同学也是跃跃欲试.笔者在一旁静观其变，看着他们“演示”，眉头舒展，这不就是自己想要的课堂吗？

只见其中一名同学拿了纸条，匆匆走上来，左手将小纸条扬起，嘴里念叨：“这好比木头.”右手轻轻一撕，一节掉在地上，再一撕，又掉了一节.

笔者进一步提示：“撕的动作像什么？”

同学们异口同声：“锯木头.”

“锯了几次？”

“两次.”

“分成了几节？”

课堂上出现了两种声音：2和3.

“到底是几节？”笔者见缝插针，然后环视课堂.

教室出现短暂安静，引起了短时间沉思……

此时，只见撕纸条那名同学高高扬起左手，“我手上还有一节呢！”他响亮的声音在班上响起.

（二）验证：切

笔者趁热打铁：“还可以用什么学习用具来分一分？”话音刚落，学生一个个忙得不亦乐乎！有人找橡皮，有人找小刀，连平时不爱发言，思考不那么积极的学生也参与进来了，忙着用小刀把橡皮切成4小块……

笔者悄悄凑过去，轻轻问：“通过操作验证，得到4块，你切了几次？明白段数与次数的数量关系了吗？”

笔者转身追问：“考试没有纸、小刀怎么办？”

（三）演示：比

在笔者的鼓励下，一名同学脱口而出：“五个指头人人有，五指之间有四空.”边说边张开右手，小手举得高高，接着又说：“指头是段数，空是次数.”这是笔者想看到的，在操作中，学生有了体验，也有了想法.

（四）深究：画

接下来，笔者不急于点评和讲解，而是鼓励学生继续思考：“段数多，手指不够用怎么办？”引导学生通过画图来解决问题.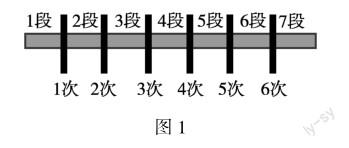

“由图可知，段数=次数+1.”

“真是这样啊！”一片赞许目光投向这名同学.

随即质疑：为什么要加1？

学生声音洪亮：我们是通过数来确定的.

“真的吗？”接着反问，环顾四周，全堂哑然.笔者举起左手，张开五指，进行示范.同学们也情不自禁地效仿起来，伸出左手，张开五指.

笔者接着举起右手，伸出食指，先点在左手的大拇指上，慢慢移到指缝处，再将食指点在左手的食指上，慢慢移到指缝处进行演示……提示：从大拇指开始，有第一个指缝与大拇指对应，有第二个指縫与食指对应，以此类推，无名指对应第四个指缝，它们是不是都是一一对应的？

“一一对应.”学生们大声附和.

“那么小手指有没有指缝与它对应？”

“没有.”

追问：“怎么办？”话音未落，“加1”，声音响起.

此时，笔者赶紧趁热打铁：再来看黑板上的这个图形，你们有什么发现？扫视课堂，同学们个个摩拳擦掌，手举得一个比一个高.笔者指名回答.“下面的1次对应的是上面的第1段，以此类推，6次对应的是上面的第6段，7段就没有对应的次数了.”

追问：怎么办？

“加1.”铿锵有力的声音在教室里回响！

“通过一一对应地数手指与指缝、段数与次数，同学们有什么体会或发现？”

“体会到它们之间是一一对应的.”

质疑：它们之间有什么关联？

“没有对应的，就要加1.”同学们脸上露出会心的笑容.

请同学们闭上眼睛，想象自己正在听一段自己最喜欢的悠扬音乐，然后想一想段数与次数的对应关系以及数量之间的内在联系.

“现在同学们都会了吗？”

学生们纷纷点头，齐刷刷地写出答案：4-1=3（次）；12÷3=4（分钟）；7-1=6（次）；6×4=24（分钟）.

（五）拓展：型

通过师生间的互动，学生们有了初步的想法，也有了由“数”到“形”，再由“形”到“型”的体验.接下来，引导学生思考：是不是可以用上面的方法去解决楼梯、时间、栽树等一系列问题？

1.有了初体验，可以出几个相关题目，让学生练一练.

（1）如果每上一层楼梯需要1分钟，那么从一层到四层需要多少分钟？

（2）时钟4点钟敲4下，12秒敲完，那么6点钟敲6下，几秒敲完？

（3）在一块三角形的空地边上栽树，每边栽5棵，那么最少栽几棵？

2.要求：学生根据题目意思，动手画一画图形.

從以上成果中不难看出学生学会了将数学文字转变为数学图形，会运用数形结合方法去解决问题.

笔者由数入手，引出“图形”概念，通过图形“形象”，让学生辨析出锯木头中的数量关系，找出一一对应的关系，然后通过三个相关题目拓展训练，让学生找到解决一般性问题的策略，由点到面，实现形象思维向抽象思维的突破，帮助学生建立数学模型，给学生渗透“数形结合”思想.

三、重视体验，融入思想

如何让学生形成模型概念，逐渐萌生“数形结合”思想？笔者设置了撕、切、比、画、型五个教学环节，前四个环节设计四个问题串：“撕”有几节？“切”有几块？“比”有几空？“画”有几段？引导学生运用演示、自主操作、验证、绘制图形四种方法，使学生的思维层层递进、步步深入，从感知开始形成表象，再由表象逐步发展为抽象思维.有了前面的铺垫，最后上升到第五个环节“型”，将抽象思维推向数学模型.这个过程既促进了知识的形成和生长，又助力了思维的发展，使学生的学习兴趣被激发，既独立思考、主动探究，又合作交流、积极参与，让学生思维的火花发生碰撞，在自我探究中体验成功的快乐.

（一）从分到“数形”———启发思维，见数“拟形”

解题的关键：让学生找到段数与次数之间的数量关系.“授人以鱼不如授人以渔”，通过两名学生的争论，通过“撕”或“切”的动作，做出“锯”的行为，将数学上如何“分”在讲台上演示出来，这样的“具象”过程符合小学生具体形象思维的特点，为“数”做好铺垫，之后小达人陈同学的“五个指头人人有，五指之间有四空”，为“形”做出展示，“指头是段数，空是次数”，为“形”做出结果，对“分”进行验证.这样像电影画面一样一幅一幅展现，可启发学生的思维，使学生学会“见数拟形”，从而渗透“数形结合”数学思想.数学思想的渗入离不开“形”.

（二）从画到“数形”———助力思维，见数“思形”

良好的开端是成功的一半.看见“潜力生”和“无力生”都参与进来，一个个都张开思维的翅膀，课堂探究的气氛如此热烈，笔者抓住学生认知的生长点，赶紧趁热打铁，一句“段数多，手指不够用怎么办？”的追问，立马达到“抛砖引玉”的效果，智慧星李同学的回答“这还不简单吗，我可以画图呀！”像一只巨手，不知不觉地把学生的思维向前推进了一大步.学生透过文字和数字可以想到图形，画出“图形”，然后阅读“图形”，辨析出数量关系.学生通过“画图”找到一条由具体题目拓展延伸到一类数学题目的解决路径.这个人人思考、层层探究的过程为学生提供一个“高德地图”，使学生在遇到同类题型的不同数量关系时就会“按图索骥”“见数思形”，进而提升思维能力.数学思想的生长离不开“形”.

（三）从想到“数形”———升华思维，见数“塑型”

数学思想是人们对数学理论与内容的本质认识.对于数与形，我国著名的数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微.”小学阶段是数学教育的启蒙阶段，向小学生渗透一些数学思想是必要的.学生运用数学方法解决问题的过程就是感性认识不断积累的过程，当这种量的积累达到一定程度时就会产生质的飞跃，从而上升为数学思想.

相比教师枯燥抽象地“说”，学生不停地“想”更有效！“想”就是一个人的大脑的思索过程.学生通过数手指与指缝，体会手指与指缝、段数与次数的一一对应关系，通过进行拓展练习，在解决问题中经历“想”的过程，发现并运用这种“一一对应关系”.“想”就是对这种“一一对应关系”进行抽象的过程，抽象出结果的过程恰恰是数学模型形成的过程.这里“一”可以代表1个人、1盆花、1棵树、1面旗、1个间隔……通过数形结合，学生发现了规律，形象思维升级成抽象思维.在解决不同题目时，“具象”到“抽象”的思维活动得到复制与粘贴，推动学生思维能力的升华，使学生在脑海里自然而然地树立起模型意识，做到“见数塑型”，从而形成模型意识.数学思想的形成更离不开“型”.

在小学数学教学过程中，学生在自助、互助、师助中体验学习乐趣，教师鼓励学生在交流、碰撞中掌握知识和技能，使学生在探究中获得成功的喜悦，帮助学生建立模型意识，促进学生形成与发展数形结合思想.

【参考文献】

[1]张颖.基于数形结合思想的小学数学“四画”教学策略研究[J].数学教学通讯，2023（7）：43-44，47.

[2]范东萍.数形结合思想在低年级数学的实践研究[J].教学管理与教育研究，2023，（5）：85-87.

[3]赵红莉.立足核心素养感悟数形结合思想[J].试题与研究，2023（5）：141-143.

[4]张卫星.数形结合让数学学习可视化[J].教学与管理，2020（26）：34-36.