Ansys_Workbench优化模块结合极限载荷分析在工程设计中的应用
2023-02-18左安达赵媛媛
左安达 赵媛媛
(1.惠生工程(中国)有限公司 上海 201210)
(2.济南惠成达科技有限公司 济南 250100)
目前压力容器设计方法中,基于弹性失效准则的规则设计占据主导地位,也能够解决绝大部分常规设备的设计任务,但随着石油化工行业的发展,承压设备越来越大型化和复杂化,在工程设计中,经常会遇到结构比较特殊,且缺少设计理论和设计方法的问题。近些年来,随着数值方法尤其是有限元法的不断发展和完善,基于有限元法和各种先进设计理论的发展研究,分析设计作为一种先进的设计理念和方法在压力容器行业中得到越来越广泛的应用。其一,分析设计可以解决规则设计无法解决的问题;其二,分析设计采用更为符合实际的弹塑性失效准则和塑性失效准则,其先进性在设备设计上的优势主要体现在可将原本粗大笨重的设备进一步的优化,能大大减少设备材料浪费,降低制造成本。目前分析设计理念中最为广泛应用的是基于弹性计算结合塑性失效理论的应力分类法,但这种方法存在其固有的自身缺陷,在工程设计中往往会出现或保守或冒进的弊端[1,2]。分析设计作为一种不断进行技术更新的方法,随着塑性理论和非线性有限元方法的日趋成熟,相继又推出了更为先进的极限载荷分析法,极限载荷分析可避免应力分类法的缺陷,在评定准则和结果的准确性方面也优于应力分类法,在特定时候可作为应力分类法的一种弥补验证方法[3]。大型有限元软件的发展和成熟为这些先进的方法提供了便捷、有效、准确的实现途径,本文便基于有限元软件Ansys_Workbench中的Direct Optimization直接优化模块,提出了一种将其与应力分类法、极限载荷分析相结合的结构优化方法,结合工程实际对一台圆筒体上开有非径向偏心大接管的设备进行局部特殊结构的优化分析。在工程设计中,结构优化设计一直是研究者和工程技术人员最为关注的问题之一,本文提出的方法便为工程设计提供了一种可实现的优化思路。
1 设计性能参数及有限元模型
1.1 设计性能参数
某项目一台设备圆筒体上开有一个非径向偏心大接管,此接管为工艺管线并与外部管道连接,由于热膨胀产生了较大的附加管道载荷作用在设备筒体上。本设备无疲劳工况,设计压力较低,仅在设计压力作用下满足筒体和接管刚度、强度所需的初始壁厚较小,但因非径向偏心大开孔的存在,使得筒体强度极大的削弱,需要对筒体进行开孔补强计算,另外因外部附加管道载荷的存在还需对接管与筒体连接处的局部应力进行校核,但此接管开孔率过大且非径向,已超出了所有开孔补强和局部应力计算方法的适用范围,因而只能采用有限元软件,综合考虑设计压力、开孔补强要求及附加管道载荷的影响进行分析计算,并最终确定筒体和接管所需壁厚[4]。根据设计压力初步试算结果,在满足刚度需求的前提下将筒体和接管初始厚度取为10 mm,根据JB 4732—1995《钢制压力容器——分析设计标准(2005年确认)》标准中应力分析法对接管根部圆角半径的要求,筒体与接管连接处外倒圆角初始半径取为20 mm、接管根部内倒圆角初始半径均取为5 mm,用于有限元模型的初始建模和后续进一步的优化分析[5]。本设备详细设计参数、结构尺寸见表1。

表1 设计参数和结构尺寸
1.2 有限元模型
本设备采用有限元软件Ansys_Workbench建模,有限元模型为圆筒体上开孔接管的局部模型,除需考虑设计压力、附加管道载荷外,其余载荷如设备自重、液柱静压力、风载荷、地震载荷及内装物料重量等均不需要考虑。本计算模型几何结构非对称,采用局部全模型建模,筒体和接管的伸出长度均远大于边缘应力衰减长度的要求,选择Solid 186单元并划分全六面体网格,局部高应力区网格加密,网格平均质量为80.6%,能够保证模型求解的准确性和精度要求。边界条件和载荷的施加:筒体和接管内表面均施加设计压力;筒体一端施加轴向和环向位移约束,另一端施加相应等效压力;接管端面施加相应的等效压力;采用质量点耦合法在接管根部施加管道载荷[6]。需指出的是,在后续优化分析过程中,接管与筒体的厚度会发生变化,端部的等效压力也应随之变化,但基于工程经验可知,等效压力的变化对最终计算的应力结果影响甚微,因而在优化分析中将施加的等效压力作为定量来考虑。有限元初始模型网格划分、边界条件和载荷的施加如图1所示,计算及应力评定所需的材料性能参数见表2。

表2 材料性能参数

图1 有限元初始模型网格划分、边界条件和载荷的施加

图1 有限元初始模型网格划分、边界条件和载荷的施加(续)
2 直接优化分析确定最优结构尺寸
2.1 基于应力分类法确定优化准则
基于有限元初始模型的计算结果,可知最大应力点值为455.34 MPa,位于接管与筒体近切向连接处外倒圆角面附近,通过最大应力点自定义一条路径(Path,如图2所示),得到此路径上的薄膜应力为296.33 MPa、薄膜+弯曲应力为435.35 MPa。根据应力分类法的评定原则,对于无疲劳工况的设备,需对由薄膜应力、弯曲应力构成的SI、SⅡ、SⅢ、SⅣ逐级进行强度评定。根据此模型中应力产生的原因、特点及危害性,可判断出此路径上的薄膜应力性质应为局部薄膜应力SⅡ,根据标准要求需将其控制在SⅡ≤1.5Sm范围内;而对于此处弯曲应力性质的判断,多年来一直难以确定,一种常见的做法是将弯曲应力全部归类为二次应力按SⅣ≤3.0Sm进行评定,直接忽略SⅢ不评定,对于本文非径向偏心大开孔接管模型,筒体与接管连接处弯曲应力成分既有一次应力又有二次应力(而有限元软件中无法区分),那么仅按SⅣ评定而不评SⅢ可能会存在着很大的不安全性,但若全部归类为一次应力按SⅢ≤1.5Sm进行评定,此时是安全的但又被指过于保守。本文目的是为对模型进行优化分析,不能按激进的方法进行评定,否则就失去了优化的意义,故选择按偏保守的评定方法SⅣ≤3.0Sm对初始结构进行优化分析。本初始模型计算结果按应力评定原则:SⅡ=296.33 MPa≥ 1.5Sm,SⅣ=435.35 MPa≥3.0Sm,应力强度评定均不通过。因此需对该初始模型进行优化以满足强度评定的要求,并确定优化准则:SⅡ≤1.5Sm,SⅣ≤3.0Sm。在优化分析过程中最大应力点位置可能会因接管与筒体相对厚度的变化而发生变化,通过最大应力点定义的路径也会有偏差,但为更好地应用本文的优化方法,需忽略这些影响较小的次要因素,计算误差在工程可接受范围内即可。

图2 有限元初始模型计算结果及通过最大应力点的路径
圆筒体非径向开孔接管连接处应力复杂且在管道载荷的作用下无明显规律,但多年研究表明,该处应力在结构方面主要由接管相对于筒体的开孔率、接管与筒体的绝对厚度、接管与筒体的相对厚度比、连接处外倒圆角半径及接管根部内倒圆角半径有关。本设备圆筒上接管开孔率一定,因而分离出4个对应力有影响的因素:筒体壁厚、接管壁厚、圆筒与接管连接处外倒圆角半径及接管根部内倒圆角半径。由前文表述可知,本设备并非由设计压力决定,更多是由开孔补强计算要求、管道载荷引起的局部应力要求来决定的,正常情况下采用有限元计算,需要通过人为调整这4个因素不断进行试算并最终确定所需壁厚及倒圆角半径,以降低应力实现对结构的优化,但这种方法人为地造成了工作量的极大增加,且难以寻求到最优的平衡解。而有限元软件Ansys_Workbench自带的Direct Optimization模块可直接自动优化,本文便基于此优化模块,提出了一种将其与应力分类法、极限载荷分析相结合的结构优化思路,为工程设计寻求结构最优解提供了可实现的方法。
2.2 优化流程及结果
Direct Optimization(直接优化)模块是根据输入输出参数设计函数关系来筛选出最佳设计点,内置有多种算法。基于本文多自变量、多目标函数的优化需求,采用MOGA(多目标遗传算法)进行优化分析:该法是一种迭代的多目标遗传算法,支持多种目标和约束,要求输入连续的参数,非常适合用于计算全局最大值或最小值,其目的是找到全局最优,同时可以规避局部最优的陷阱[7-8]。
基于上述分析,本文将筒体壁厚T、接管壁厚t、连接处外倒圆角半径R及接管根部内倒圆角半径r这4个影响参数作为设计自变量,根据有限元初始模型的计算结果、相关标准中的规定及工程经验将自变量变化范围分别定为:10 mm≤T≤30 mm,10 mm≤t≤60 mm,5 mm≤R≤60 mm,1 mm≤r≤5 mm;将路径Path上提取出的SⅡ和SⅣ作为目标函数建立优化模型:SⅡ≤1.5Sm=187.35 MPa和SⅣ≤ 3.0Sm=374.7 MPa。为更直观地探究4个参数对目标函数SⅡ和SⅣ计算结果的影响,先进行单因素多目标分析,即分别将其中1个参数作为自变量,其余3个参数作为定量来分析,以考察各个参数对SⅡ和SⅣ应力强度的影响规律。MOGA算法设置中,将初始样本容量设定为100,每次迭代产生的样本数为50,最大迭代次数为20次,迭代收敛后提取并优化数据得到SⅡ和SⅣ应力强度随每个参数变化趋势,如图3所示。

图3 优化分析后SⅡ和SⅣ应力强度随每个参数变化趋势
由图3的变化趋势图可直观地看出各个参数对SⅡ和SⅣ应力强度的影响规律。由图3(a)分析可知:筒体壁厚T的增加可显著降低局部薄膜应力强度SⅡ和局部薄膜+弯曲应力强度SⅣ的值,因为筒体壁厚的增加直接增加了筒体的强度和刚度,可使得连接处筒体端局部薄膜和弯曲应力直接降低缓解,但同时也可看出筒体壁厚并非越厚越好,当筒体壁厚增加到一定值时,对降低应力强度值的作用越来越小,相反还会造成应力的进一步增大。原因在于筒体壁厚过大时,与接管的相对比值越来越大,两者的刚度比过大造成变形协调性越来越差,使得连接区域局部薄膜和弯曲应力不减反增。由图3(b)分析可知:接管壁厚t的增加可使得接管的强度和刚度增加,在连接处接管端可起到一定的降低应力的作用,但因接管直径较小,对应力值降低程度有限,幅度较小,随接管壁厚继续增加到一定程度,会造成接管刚度过大,而筒体刚度过小,也会出现两者的刚度比过大造成的变形协调性越来越差,使得连接区域的局部薄膜和弯曲应力都转移到筒体端,造成筒体端的应力值幅度增加较大,最终造成连接处局部薄膜和弯曲应力同样不减小、反而大大增加。由图3(c)分析可知:连接处外倒圆角半径R的增大,可缓解连接处的总体结构不连续性,使得变形协调性得到一定的缓解,应力值有小幅降低,但作用有限。因为外倒圆角的增大,主要作用是能降低连接处的峰值应力,而对降低局部薄膜和弯曲应力的作用很小,但通过计算结果可知,本模型最大应力点位置处(近乎切向)的峰值应力本身就很小。由图3(d)分析可知:接管根部内倒圆角r的改变无论对局部薄膜还是对弯曲应力的影响都很小,一方面是因为本模型最大应力点在外倒圆角处,另一方面同样是因为内倒圆角的大小仅对降低峰值应力有一定作用,而对降低薄膜和弯曲应力的作用很小。
通过分析上述4个参数对有限元初始模型中局部薄膜和弯曲应力的影响规律,可知增加内、外倒圆角半径对降低该模型最大应力位置处局部薄膜和弯曲应力值所起的作用很小,而增加筒体和接管壁厚是最直接有效的方法,但也并非越厚越好,而应该选取合适的绝对厚度和相对厚度比(刚度比不能过大),才能在不盲目增加厚度、成本的前提下,以达到最优最有效的降低应力的作用。基于上述分析,便可将有限元初始模型进一步调整为:接管根部内倒圆角半径r保持不变,仍为5 mm,圆筒与接管连接处外倒圆角半径R由20 mm调整到40 mm,并将这2个参数调整为定量参数,而将筒体壁厚T和接管壁厚t仍作为自变量参数,便将原本的4个自变量参数变为2个,再次采用MOGA算法和同样的目标函数进行1次2因素2目标函数的优化分析,以寻求到满足目标函数的最优解。经过多次迭代求解后收敛,并提取部分优化后的数据列于表3。
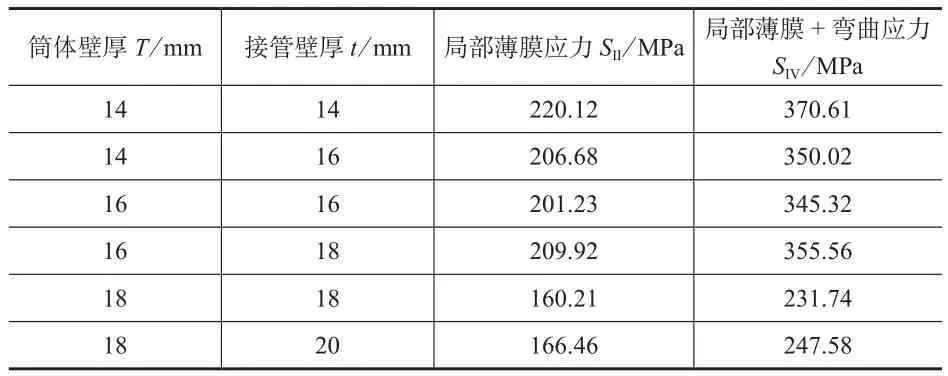
表3 优化后选取的10组数据
根据应力强度评定准则,SⅡ≤1.5Sm=187.35 MPa和SⅣ≤3.0Sm=374.7 MPa,并由表3分析可知:当筒体厚度T=18 mm、接管壁厚t=18 mm时,局部薄膜应力为160.21 MPa,满足SⅡ≤1.5Sm的强度评定要求;局部薄膜+弯曲应力值为231.74 MPa,满足SⅣ≤3.0Sm的强度评定要求。同时可看出,当接管壁厚增大到t=20 mm时,局部薄膜应力和弯曲应力值反而有微小增大,也进一步验证了前文的观点:接管与筒体的相对厚度比不宜过大,否则会使得应力产生不减反增的相反效果。需特殊说明的是,虽然本文模型在筒体和接管壁厚均取18 mm时按SⅡ和SⅣ评定均合格,但基于本文2.1节的分析,此非径向偏心大开孔接管模型筒体与接管连接处弯曲应力成分既有一次应力又有二次应力,且如果一次弯曲应力占比很大,那么将弯曲应力全部归类为SⅣ来评定而不评SⅢ可能会存在很大的不安全性,会有发生塑性垮塌失效的风险;若全部归类为SⅢ=231.74 MPa则不满足SⅢ≤1.5Sm=187.35 MPa的评定要求,则还需继续对本模型筒体和接管调整加厚以满足要求,但又可能会偏保守造成材料成本的浪费。基于此,本文对此优化后的模型采用极限载荷法进一步分析验证以保证不会发生塑性垮塌失效,以避免应力分类法因无法区分一次弯曲和二次弯曲应力成分的缺陷可能带来的误判。
3 极限载荷分析的进一步验证
本文极限载荷分析采用在工程应用中直接可靠的载荷系数法,根据载荷系数法的设计准则,本模型需按载荷组合工况1.5(P+Ps+D)进行计算和评定,合格评定准则为计算结果收敛。其中,P为设计压力,Ps为液柱静压力,D为容器自重、内装物料、附属设备及外部配件的重力载荷。本模型中液柱静压力、容器自重、内装物料等对所考虑的接管部位应力影响极小,可忽略不计;管道外载荷可看作外部配件的重力载荷予以考虑。极限载荷分析中采用双线性等向强化模型,将切线模量设置为0并定义屈服强度为187.35 MPa[9]。有限元软件经过53次迭代后收敛,极限载荷分析计算的等效应力/应变云图和载荷位移曲线分别如图4和图5所示。

图4 极限载荷分析计算的等效应力/应变云图

图5 载荷-位移曲线
由图4可看出,载荷组合1.5(P+Ps+D)计算工况下,本模型最大等效应力值为200.93 MPa,稍大于材料屈服强度,理论上计算值是不应该超过屈服强度的,原因在于有限元软件计算的应力精确值是在高斯积分点上,而云图中显示的则是单元节点上的应力值,该值是由高斯积分点上的应力值通过插值外推到节点上的,故云图上的应力值与屈服强度会略有差别[10]。本模型计算最大等效塑性应变为0.0010048 mm,由图5中载荷-位移曲线也可看出,其斜率几乎未有变化,表明在此位置区域结构虽已进入塑性变形阶段,但塑性变形极其微小。基于上述分析:1)极限载荷计算的结果是收敛的,则按评定准则表明该结构强度是能够保证的;2)本模型只在接管根部局部区域产生极其微小的塑性变形,不足以使整个结构发生塑性垮塌失效,故本模型的极限承载能力是完全能满足设计条件的。通过上文一系列的优化和分析确定本模型最终优化后的工程设计尺寸取值为筒体壁厚T=18 mm,接管壁厚t=18 mm,筒体与接管连接处外倒圆角半径R=40 mm,接管根部内倒圆角半径r=5 mm,是满足强度和刚度需求最优、最经济合理的设计方案。
4 结论
本文基于有限元软件Ansys_Workbench中的Direct Optimization直接优化模块,提出了一种将其与应力分类法、极限载荷分析相结合的结构优化方法,结合工程实际对一台圆筒体上开有非径向偏心大接管的设备进行局部结构优化分析,并对此方法的优化流程和步骤归纳如下:
步骤1:根据设计压力采用常规计算方法进行初步试算,在满足强度和刚度的前提下,结合相关标准的要求确定结构的初始模型尺寸,用于后续有限元模型的初始建模和进一步的优化分析。如本文中将筒体和接管初始厚度取为10 mm,筒体和接管连接处外倒圆角初始半径取为20 mm,接管根部内倒圆角初始半径取为5 mm。
步骤2:根据结构的几何特性、载荷作用等情况分析,准确合理地建立有限元初始模型,划分高质量的网格,并设置准确的载荷和边界条件,以符合工程实际并获得准确的有限元计算结果。如本文中采用局部全模型建模,选择Solid 186单元划分全六面体网格并在局部高应力区网格加密等系列设置。
步骤3:基于有限元初始模型的计算结果,通过最大应力点定义一条路径,得到此路径上的薄膜应力、薄膜+弯曲应力,结合应力分类法的基本原理和评定准则,确定优化准则。如本文中通过分析将路径上的薄膜应力按SⅡ≤1.5Sm,薄膜+弯曲应力按SⅣ≤3.0Sm作为优化准则,以达到优化目的。
步骤4:基于理论知识和经验认知,分析出会影响结构应力的影响因素,并确定为自变量参数,将优化准则SⅡ≤1.5Sm和SⅣ≤3.0Sm作为目标函数,采用MOGA算法,先进行单因素多目标分析。如本文中将4个影响因素T、t、R、r作为自变量参数,将其中1个因素作为自变量,其余3个作为定量,以探究各个参数对SⅡ和SⅣ应力强度的影响规律。
步骤5:基于单因素多目标的优化分析结果,判断出哪些因素对应力影响较大,哪些因素对应力影响较小,将影响较小的因素调整为定量参数,减小自变量个数,而影响较大的因素仍作为自变量参数,进一步采用多因素多目标分析,以寻求满足目标函数的最优解。如本文中分析出R和r对应力影响很小,便将此2因素调整为定量参数,而T和t仍作为自变量参数,将原本的4个自变量参数变为2个,再进行1次2因素2目标函数的优化分析,最终得到最优的T值和t值。
步骤6:根据优化后的结构尺寸修改有限元模型,采用极限载荷分析对优化后的模型进一步分析验证,如果极限载荷分析评定通过,则可确定为最终优化尺寸,如不满足则还需对模型进一步优化调整。原因在于:本模型中非径向大开孔接管连接处弯曲应力既有一次成分又有二次成分,优化准则中仅采用SⅣ≤3.0Sm对薄膜+弯曲应力评定,存在很大的不安全性。如本文中模型通过极限载荷分析验证,便可最终确定出满足强度和刚度需求的最优尺寸为:T=18 mm,t=18 mm,R=40 mm,r=5 mm。
本文提出的优化方法的准确性、可靠性、实用性还需要更多的理论和实际案例进行进一步验证,更为重要的是为工程设计提供了一种可实现的优化思路。
