基于图神经网络的复杂网络关键节点检测算法

陈 娜

(山西工程科技职业大学 计算机工程学院，山西 晋中 030619)

0 引言

关键节点[1]在复杂网络中处于重要地位，其行为对复杂网络中的信息传播具有极大的影响，分析并预测大规模复杂网络的关键节点在舆情传播、政策宣传和商业营销等领域均具有巨大的应用价值[2]。目前主流的关键节点挖掘方法根据技术差异可分为4类[3]：基于评分规则的方法、基于复杂网络图的方法、基于影响传播模型的方法以及多维融合的方法。其中复杂网络图[4]包含了丰富的网络结构信息，通过拓扑结构寻找关键用户，具有准确、高效的优点。度中心性[5]、接近中心性[5]、中介中心性[6]可从不同角度评估节点在网络中的重要性，但这3种评价方法的可靠性均不足。PageRank算法[7]是一种迭代的节点关键性评估指标，该指标基于特征向量中心度(Eigenvector Centrality)提高了评估的可靠性，但其计算量大，难以适用于大规模复杂网络。

研究者们尝试通过图计算理论[8]挖掘复杂网络图的隐含信息，以分析复杂网络中节点与连接的关键性。然而，图计算理论不具备自主学习的能力，因此可扩展性与可靠性均较弱。近年来，图神经网络(Graph Neural Network，GNN)的出现促使人工智能步入“认知智能”时代[9]，现已被成功用于求解推荐系统[10]、数据聚类[11]以及图像处理[12]等问题，并展现出极大的发展潜力。通常，复杂网络中节点的邻居节点影响力越大，其自身影响力也越大，而GNN的核心思想是借助神经网络的权重参数将邻居节点信息纳入当前节点，因此GNN可自动考虑节点相关的复杂网络拓扑信息。由现有的相关研究成果可知，虽然GNN能自主学习输入图模型的拓扑信息，且具有较强的可扩展能力，然而，GNN在大规模数据上的训练难度较大，且无法自适应地处理动态变化的网络问题。

诸多学者将强化学习(Reinforcement Learning，RL)技术[13]引入到深度神经网络的训练阶段，通过RL提高深度神经网络的自学习能力。目前利用RL成功训练的神经网络模型主要有：循环神经网络[14]、递归神经网络[15]和径向基函数神经网络[16]等，RL技术不仅能增强神经网络的自学习能力，而且提高了神经网络在不同任务上的应用效果。受上述研究成果启发，本文利用RL技术训练GNN，增强GNN的自学习能力，进而提高复杂网络关键节点检测算法的可扩展性与可靠性。

本文将复杂网络建模为图模型，采用双重鲁棒性指标作为节点的关键性评价标准，然后利用GNN的节点嵌入模块学习复杂网络节点的拓扑结构信息，利用回归模块推理节点的关键性评分。此外，提出了基于RL的GNN训练方法，该方法通过奖励函数学习GNN的超参数并输出一个动作序列，该动作序列对应该复杂网络关键节点识别的GNN模型。实验结果表明，本算法使用GNN检测的关键节点具有较高的准确性，且检测速度较快。

1 网络模型

假设G=(V,E)表示一个图，V与E分别为图的节点集与连接集，关键节点检测问题可描述为搜索一个关键节点子集Vc，该子集对图的鲁棒性具有极大的影响。假设u为复杂网络的一个节点，v=N(u)为u的邻居节点集，那么u的关键性评分函数可表示为：

ru=f(hu,hv)，

(1)

式中，hu，hv分别为节点u与v的特征向量；ru为关键性评分。GNN在训练过程学习复杂网络的关键性评分关系f()，输出预测的关键性评分关系f′()。

2 基于GNN的关键节点检测模型

GNN在复杂网络关键节点检测问题上的模型包括3部分：① 选取图鲁棒性指标评价节点的关键性，节点的关键性越高成为关键节点的可能性则越大。② 使用GNN的嵌入模块学习包含邻居信息的节点关键性评分。③ 使用GNN的回归模块推断未知节点的关键性评分。

2.1 节点关键性评估

系统鲁棒性指标在图理论中反映了某个节点缺失对图产生的影响，为了提高本算法的兼容性与鲁棒性，采用2个图鲁棒性指标评价节点的关键性：

① 有效图抗。定义为图中每对节点的有效阻抗总和。有效图抗Rg的计算方法为：

(2)

式中，λi为图G的拉普拉斯矩阵特征值；c为G包含的连接总数量。

② 加权谱。定义为图中n-圆环的正则化总和。将n-圆环定义为一个节点序列u1,u2,…,un，其中ui与ui+1相邻。加权谱Ws的计算方法为：

(3)

式中，n为圆环形状，例如，n=3表示图中的三角形数量，本文复杂网络问题中将n设为4。

2.2 节点嵌入模块

GNN第1个子模块基于图拓扑结构信息与节点关键性评分学习复杂网络每个节点的嵌入向量。如果节点在复杂网络中距离越近，那么节点在嵌入空间中距离也越近。GNN将复杂网络节点映射到嵌入空间的流程如图1所示。

图1 GNN的节点嵌入模块Fig.1 Node embedding module of GNN

节点嵌入模块包含2个步骤：

步骤1：根据每个节点及其邻居节点学习一个描述符。假设邻居跳数为K，例如，K=2表示目标节点2跳距离以内的节点为该节点的邻居。节点u的邻居节点可表示为：

N(u)={u:D(u,v)≤K,∀u∈G}，

(4)

式中，函数D()计算2个节点之间的最小跳数；u为目标节点；v为图中的其他节点。

步骤2：通过聚合函数为每个节点创建一个邻居嵌入，并为每个邻居嵌入分配一个权重。通过注意力模块自动学习每个邻居节点的权重，该步骤的数学模型可定义为：

(5)

图G中全部节点的嵌入可定义为：

(6)

算法1描述了节点嵌入表示的处理流程。

算法1 节点嵌入表示算法输入:图G,输入节点特征Xv,组合权重W,聚合权重Q。输出:节点嵌入向量zv。1.h0v=Xv;∥初始化阶段2.foreach l from 1 to L do3. foreach v from 1 to V do4. hlN(v)=Att(Qlhl-1k);5. hlv=ReLU(Wl[hl-1v‖hl-2v‖hlN(v)]); ∥ ‖.‖表示聚合运算6. endfor7.endfor8.return hlv;

2.3 回归模块

图2 GNN的回归模块Fig.2 Regression module of GNN

(7)

2.4 节点关键性评分预测模块

GNN预测复杂网络中节点关键性示意如图3所示。GNN模型预测输入复杂网络各节点的关键性评分，将复杂网络的节点按关键性降序排列。

图3 复杂网络节点的关键性预测示意Fig.3 Cruciality prediction diagram of complex network nodes

3 GNN的训练方法

在训练阶段需确定GNN的超参数，包括GNN的深度、每层的神经元数量以及激活函数。GNN在复杂网络上的训练流程如图4所示。

图4 GNN在复杂网络上的训练流程Fig.4 GNN training process on complex networks

3.1 传统GNN训练方法

GNN的激活函数设为ReLU(Rectified Linear Units)函数，使用Adam优化器[17]对节点的关键性排名损失进行优化，Adam优化器的参数设为TensorFlow-Keras框架[18]的缺省值，在TensorFlow框架中使用Stellargraph作为图计算的库。

算法2描述了传统的GNN训练流程。每次迭代将节点嵌入与邻居嵌入作为输入数据，运行GNN节点嵌入模块计算每个节点的嵌入向量；然后，GNN回归模块基于上述嵌入向量计算节点的关键性评分。根据节点关键性评分估计值与实际值之间的差异来训练GNN。重复运行上述程序，产生训练的GNN模型。

算法2 GNN的传统训练方法输入:复杂网络图G,最大迭代次数I,GNN的深度空间与每层的节点数量空间。输出:GNN超参数1.计算G每个节点的实际关键性评分值;2.foreach i from 1 to I do3. 运行GNN节点嵌入模块产生节点的嵌入表示;4. 运行GNN回归模块估计节点的关键性评分;5. 更新式(7)的权重;6. 更新GNN的深度;7.更新GNN每层的节点数量;8.endfor9.在复杂网络测试集G'上运行GNN;10.输出G'的top-N关键节点;

3.2 基于RL的GNN训练方法

借助RL框架训练GNN，训练目标是最小化节点关键性评分估计值与实际值之间的差异。RL的状态为GNN的预测性能，动作为GNN超参数，RL通过奖励函数寻找预测最准确的GNN模型。

3.2.1 RL框架

RL框架主要由状态S、动作A与奖励R三个元素构成，其目标是Agent通过执行不同的动作来最大化总奖励。Agent在每个时间步重复执行如下的步骤：若Agent在时间步t的状态为S，此时Agent选择执行动作A，然后从当前环境获得一个奖励R。本文采用Q-learning作为RL框架，若当前Agent的最优策略为π:S→A，那么环境奖励可表示为：

q(st,at)=γRt+γ2Rt+…+γnRn，

(8)

式中，γ为折扣因子；t为当前时间步；s与a分别为Agent的状态与动作。

Q-leaning在每个时间步结束更新Q-table的奖励，更新的奖励可定义为：

(9)

Q-learning使用GNN预测Q-table中的奖励，即GNN作为Q-learning框架的Q-函数。给定一个输入状态S，GNN输出所有“状态-动作”的Q-值，原Q-learning在每个时间步结束更新Q-table。本文对Q-learning框架的Q-table机制进行修改，保存过去全部时间步的状态、动作与奖励值，记为Q-matrix，对Q-matrix随机采样产生一个子集，将该子集作为GNN的训练集以减少训练数据量。

3.2.2 RL奖励函数

若排除节点v导致复杂网络的鲁棒性发生大幅降低，那么节点v的关键性评分应较高。对复杂网络的有效图抗与加权谱差分值做加权调和运算，其结果作为RL的奖励。Q-learning的奖励函数可定义为：

(10)

3.2.3 RL随机采样训练

Q-matrix中保存了Q-learning所有时间步的状态、动作与奖励数据，假设Q-matrix共有M个Q-value，Q-learning训练阶段对Q-matrix随机采样K次，产生包含K个Q-value的训练集。基于欧氏距离度量实际Q-value与期望Q-value之间的距离，由此可获得每对数据的损失函数：

(11)

式中，rt表示在时间步t的第i个Q-value。

将每对训练数据的损失累加，产生训练集的总损失：

(12)

式中，i表示训练集中Q-value的索引；M表示训练集中Q-value的总数量。

4 实验与结果分析

文中使用Gephi version 0.9.2软件分析复杂网络数据，使用Python 3.6实现文中相关算法，编程环境为Pycharm与Eclipse集成的开发平台。PC机的配置为Intel Core i7-11700，主频为2.5 GHz，内存为16 GB，操作系统为Windows 10。

4.1 数据集

采用wiki vote数据集[19]作为实验的真实数据集，共包含7 115个节点与103 689条连接。数据集包含了一个用户对另一个用户的投票信息来推选Wikipedia上的关键节点。网络模块度(Network Modularity)是由Newman提出的一种衡量复杂网络中社区强度与稳定性的常用评价方法，模块度的范围为[-1，1]。wiki vote数据集的模块度为0.428，说明该复杂网络包含密集的社区结构。网络的平均集聚系数度量了复杂网络中顶点之间结集成团的程度，具体而言，反映了复杂网络中用户与相邻用户之间的密切程度。wiki vote数据集的平均集聚系数为0.140 9，说明该复杂网络中封闭三角形拓扑结构较少。综合分析wiki vote数据集的模块度与集聚系数可知，该复杂网络的社区内连接较密集，而社区之间的关系较稀疏，这也体现了当前主流大规模复杂网络的拓扑结构特点。

4.2 评价指标

本文使用中介中心度(Betweenness Centrality，BC)、度中心度(Degree Centrality，DC)与接近中心度(Closeness Centrality，CC)评估每个用户在复杂网络中的声望。此外，通过Page Rank(PR)指标评价节点在复杂网络中的重要性，PR的计算方法可参考文献[20]中的实现实例。

BC的计算公式为：

(13)

式中，c(i, j)(x)表示经过节点x的路径总数量；节点i与j表示路径的两端。

DC的计算公式为：

(14)

式中，d(x，y)表示节点x与y之间的最短路径长度；n表示与x建立路径的节点数量。

CC的计算公式为：

CC(x)=dig(x)，

(15)

式中，dig()函数为节点x的度。

节点i在复杂网络中的声望可定义为：

(16)

式中，BC(x)，CC(x)，DC(x)与C(x)分别表示节点x的中介中心度、接近中心度、度中心度与集聚系数；D为用户x与社区中心位置的距离。声望RP(x)越大，表示用户x成为关键节点的可能性越大。

4.3 GNN训练

从wiki vote数据集的7 115个节点中随机选择60%(即4 269个)作为训练集，剩余的40%(即2 846个)作为测试集。首先采用第3部分中基于RL的方法训练GNN，GNN的超参数范围如表1所示。经过训练输出的GNN超参数如下：① 节点嵌入模块的深度为4，每层的神经元数量为128，64，32，16；② 回归模块的深度为3，每层的神经元数量为12，8，1。下文采用训练的GNN网络预测测试集的社交领袖。

表1 GNN训练阶段的参数范围Tab.1 GNN parameters during training

4.4 对比算法

采用多个关键节点检测算法来构建对比实验，以全面评估各复杂网络关键节点检测算法的有效性。所考虑的对比算法包括：

FFA算法[21]：该算法是一种基于萤火虫优化算法(Firefly Algorithm)的复杂网络关键节点检测算法，先使用Louvain方法将复杂网络划分成社区，并在节点重要性评估标准中考虑了局部社区的拓扑信息，然后利用萤火虫优化算法搜索复杂网络中重要性最高的节点。

PCP算法[22]：该算法是一种基于多阶段分簇的复杂网络关键节点检测算法，通过先分簇后排名的关键节点检测策略筛选候选关键节点子集，由此避免了对网络全部节点的搜索。

OLMiner算法[23]：该算法是一种基于两阶段聚类的复杂网络关键节点检测算法，第一阶段采用社区检测技术解决社区间的影响力重叠问题，同时缩小候选子集的规模；第二阶段进一步搜索准确的关键节点。

FTS算法[24]：该算法是一种基于模糊信任系统的复杂网络关键节点检测算法，先采用模糊系统建模网络的社交关系，再利用模糊理论推断网络中最受信任的节点，从而获得复杂网络中的关键节点。

4.5 实验结果与分析

4.5.1 复杂网络关键节点检测性能实验

wiki vote数据集的复杂网络共有28个社区，首先对复杂网络全部测试集运行关键节点检测算法，输出排名最高的10个节点。表2统计了BC，DC，CC与PR对应的top10节点及其结果值。由表2可知，基于不同评价指标在同一数据集上产生的关键节点排名存在差异。为了分析各指标的综合排名结果，将每个排名中出现次数最多的节点作为该排名的正定节点，最终产生的top10节点序号分别为{3 461，568，1 725，2 896，772，3 397，3 180，6 713，5 421，4 220/5 421/75}，其中排名第10的节点中4 220，5 421和75各出现一次。

表2 wiki vote数据集各评价标准的关键节点Tab.2 Crucial nodes detected with all evaluation criterions on wiki vote dataset

各关键节点检测算法输出的top10关键节点如表3所示。

表3 各算法检测的关键节点Tab.3 Crucial nodes detected by all algorithms

由表3可知，FFA算法成功预测的关键节点排名为{1,3,7,8,9,10}，PCP算法成功预测的关键节点排名为{1,4,5,6,7,8,10}，OLMiner算法成功预测的关键节点排名为{1,2,4,6,9}，FTS算法成功预测的关键节点排名为{1,2,3,5,6,7,8,10}，GNN算法成功预测的关键节点排名为{1,2,3,4,5,6,7,8,9,10}。从各算法预测的排名结果可以看出，FTS与GNN预测的排名较可靠，FFA，PCP与OLMiner预测的排名可靠性较低。

为评估各对比算法识别全网复杂网络中关键节点的性能，建立一组对比实验：先采用各算法分别搜索复杂网络测试集top200的节点列表，再通过准确率、召回率、精度与F1-score评价识别结果与正定结果之间的匹配度，结果如图5所示。从图5可以看出，OLMiner算法的准确率、召回率、精度与F1-score均明显低于其他4种对比算法，该算法是一种基于两阶段聚类的复杂网络关键节点检测算法，其优势是通过聚类处理降低了社区间连接对关键节点识别的干扰，然而对于全网关键节点的识别性能较差。FTS算法采用模糊系统建模网络的社交关系，再利用模糊理论推断网络中最受信任的节点，其推理效果明显好于FFA算法与PCP算法。本文借助GNN的权重参数将邻居节点信息纳入当前节点，因此GNN可自动考虑节点相关的复杂网络拓扑信息，GNN的信息包含了复杂网络的全局拓扑信息与局部社区信息，因此其性能较好。观察表2的结果可知，不同评价标准所选出的关键节点存在不可忽略的差异，因此很难产生统一的关键节点集。综合而言，本文算法的关键节点命中率明显高于其他对比算法。

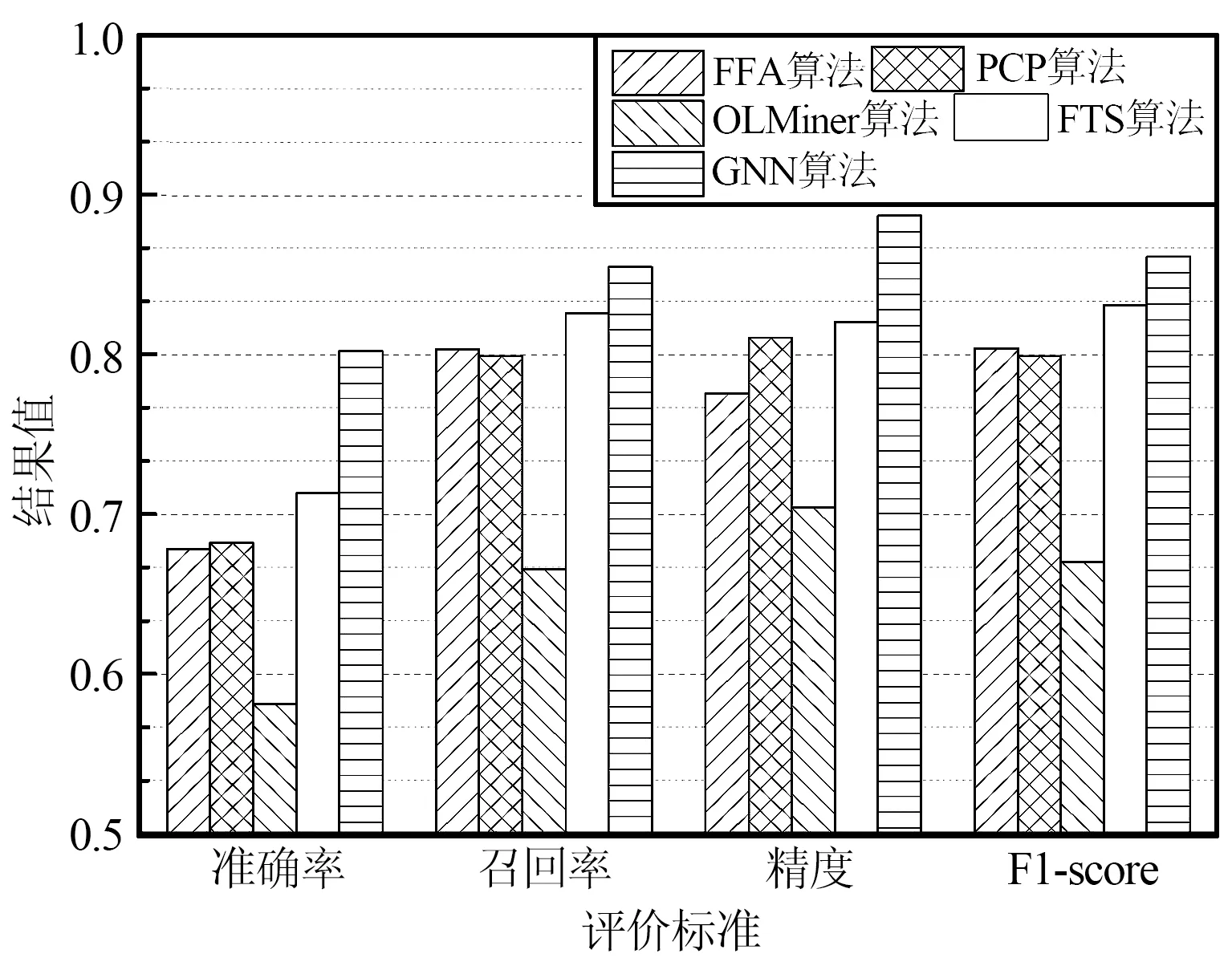
图5 复杂网络top200的关键节点识别性能Fig.5 Top200 crucial nodes recognition performance in complex networks

4.5.2 社区关键节点检测性能实验

目前，大规模复杂网络通常呈现出社区性拓扑结构的特性，节点在社区内关系紧密而在社区间关系稀疏，每个社区内的关键节点对该社区内节点的影响力较大，而对其他社区内节点的影响力较小，因此识别每个社区的关键节点也是关键节点检测算法的一个重要研究目标。wiki vote数据集的测试集共有28个社区，表4统计了BC，DC，CC与PR识别的各社区关键节点。由表4可知，基于不同评价指标产生的社区关键节点存在差异。为了分析各指标的综合识别结果，将每个社区中出现次数最多的关键节点作为该社区的正定关键节点，最终产生的top10节点序号分别为{7452233 0661 089，3 397，165，6 713，28，72，4 2204 434，75，4 4402 268，2 896，772，1 373，522，3 461，3683 398，2 849，2 990，1 725，8 493，128，5 421，1 9841 5786 8232 748，568，47}。

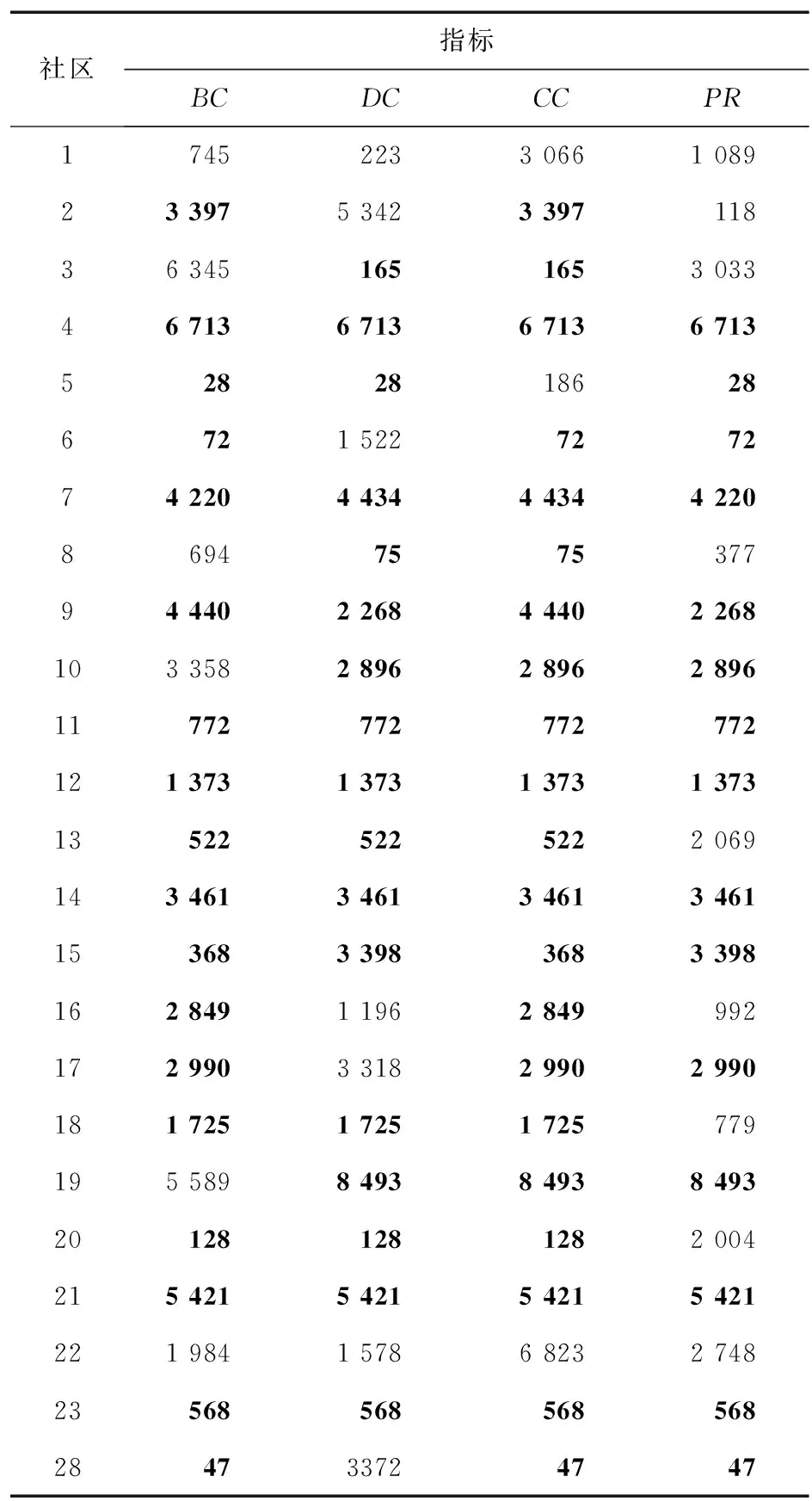
表4 wiki vote数据集各评价标准的社区关键节点Tab.4 Crucial community nodes detected with all evaluation criterions on wiki vote dataset

为了评估关键节点检测算法对社区关键节点的识别性能，运行各算法分别处理每个社区的局部数据，各算法识别的社区领袖如表5所示。由表5可知，FFA算法正确预测的社区领袖数量为17，准确率为70.83%；PCP算法正确预测的社区领袖数量为17，准确率为70.83%；OLMiner算法正确预测的社区领袖数量为15，准确率为62.5%；FTS算法正确预测的社区领袖数量为16，准确率为66.67%；GNN算法正确预测的社区领袖数量为21，准确率为87.5%。FFA算法与PCP算法均为基于社区的关键节点挖掘算法，其性能优于OLMiner算法与FTS算法。此外，GNN对全局网络与局部网络的学习能力均较强，因此GNN算法正确预测的社区社交领袖数量最多，高于其他4个对比算法。观察表5的结果可知，不同评价标准所选出的关键节点存在不可忽略的差异，因此很难产生统一的关键节点集。综合而言，本文算法的关键节点命中率明显高于其他对比算法。

表5 wiki vote数据集各评价标准的关键节点Tab.5 Crucial community nodes detected with all evaluation criterions on wiki vote dataset

4.5.3 算法效率实验

由于复杂网络具有动态变化的特点，因此计算效率是影响相关算法是否具备可扩展能力的重要因素。实验中每个算法在wiki vote数据集上独立运行10次，计算每个算法的平均运行时间，结果如表6所示。观察表6中的结果可知，OLMiner算法的平均计算时间最短，其原因主要是OLMiner算法在第1阶段采用社区检测技术以缓解社区间的影响力重叠现象，该措施大幅减小了候选子集的数据规模，有效缩短了第2阶段搜索关键节点的计算时间。然而，FTS算法先采用模糊系统建模网络的社交关系，再利用模糊理论推断网络中最受信任的节点，由于模糊系统在大数据上的工作效率较低，因此FTS算法的平均计算时间最长。本文GNN算法的平均计算时间为次优值，略慢于OLMiner算法，但明显快于FFA算法、PCP算法与FTS算法。

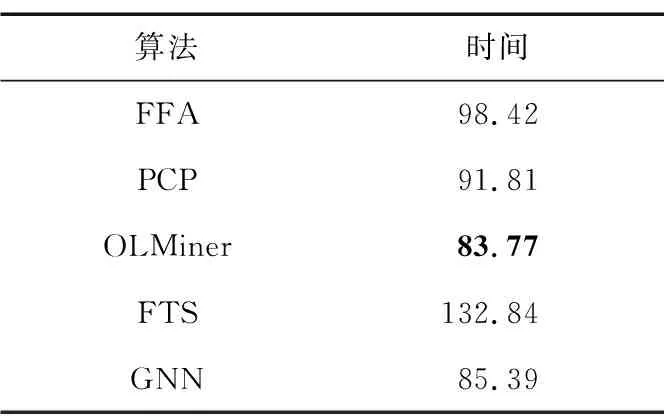
表6 关键节点检测算法的平均计算时间Tab.6 Average computation time of crucial nodes detection algorithms 单位：ms

5 结束语

为了解决传统复杂网络关键节点检测算法准确性低以及可靠性不足的问题，结合GNN模型提出了一种可扩展复杂网络关键节点检测算法。将复杂网络建模为图模型，利用GNN评估网络中节点与连接的关键性评分。在GNN训练方面，为了改善关键节点检测算法的可扩展性及可靠性，采用RL搜索GNN的超参数。通过GNN的权重参数将邻居节点信息纳入当前节点，GNN的信息包含了复杂网络的全局拓扑信息与局部社区信息，因此GNN对全局网络与局部网络的学习能力均较强，对全局复杂网络与局部社区的关键节点识别问题均达到了较好的效果。