多约束的无人机动态路径规划算法研究
2023-02-18罗银辉李荣枝潘正宵王星怡
罗银辉,李荣枝,潘正宵,王星怡
(中国民用航空飞行学院 计算机学院,四川 广汉 618370)
0 引言
多旋翼无人机具有体积小、机动性高和速度快的特点,在航拍、搜救和巡检工作中具有广泛应用。得益于智能移动设备的发展,斯坦福大学通过在无人机上搭载微机电系统(Micro-Electro-Mechanical System,MEMS)传感器加嵌入式机载电脑的方式[1],首次实现了无人机的自主飞行,此后,无人机的自主飞行研究迅速发展。无人机在自主飞行过程中,最重要的功能是路径规划与避障,即实现导航。与机器人相似,导航的目的在于找到从起点到终点具有避障能力的最优或次优路径[2]。现实中的环境是复杂多变的,无人机在飞行的过程中除了要面对静态的障碍物如树木、灯柱等,还需要面对动态的障碍物如飞鸟和其他无人机等,如何使无人机在动态环境中实现灵活的自主避障,是研究的重要方向。
本文对基于轨迹优化的动态重规划方法进行研究,采用利于重规划的高阶B样条曲线,结合提出的3项飞行约束方程,动态重规划路径;采用基于时间的再分配策略,实现无人机动态避障,解决动态重规划路径算法的实时性问题。
1 算法流程
无人机要实现自主飞行,需要通过感知系统估计出自身的状态信息,以及周围的环境地图[3]。传统的做法是将障碍物的点云图收集并转换为在三维地图中的占用栅格地图,再通过路径搜索算法计算无人机的可通行路径[4]。但这类地图在路径规划算法的应用过程中效率较低,为了更高效地获取环境信息,采用包含了梯度信息的欧式有符号距离函数(Euclidean Signed Distance Functions,ESDF)地图。基于梯度的运动规划是当前主流的无人机局部路径规划方法,该方法将问题表述为无约束线性规划。Ratliff等[5]率先将ESDF地图引入机器人的路径规划,实现了ESDF地图使用上的突破。沿着这一思路,后续研究中,许多框架直接利用梯度信息进行优化配置空间中的轨迹[6],有非常好的效果。
在路径搜索这一问题上,A*算法是一种经典的路径搜索算法,在使用A*算法进行路径规划时,虽然能找到最短路径,但A*算法不考虑无人机的动力学可行性,在实际飞行过程中,无人机可能会面临危险[7],且在面对动态环境时,A*算法并不适用[8]。文献[9]采用高阶B样条曲线进行路径规划,该方式的优点在于预规划的路径更为平滑,且有助于动态重规划。为了实现动态重规划,文献[5-6]就平滑、碰撞和可行性创建惩罚项,以此设计约束方程,对轨迹进行动态规划。
然而,部分动态规划算法会将时间这一维度抽离[10],用离散的时间进行轨迹优化。这样的方式并不适用于无人机,因为它对动态约束更加敏感。为此, Oleynikova等[11]提出了一种用于无人机规划的连续时间多项式轨迹优化方法。本文借鉴这一思想设计时间再分配策略。
文中的路径规划算法采用B样条曲线进行预规划路径,根据飞行约束方程,结合ESDF地图提供的梯度信息,实现路径搜索。在飞行的过程中,结合时间再分配策略,进行无人机飞行轨迹的动态规划,实现动态避障。算法流程如图1所示。
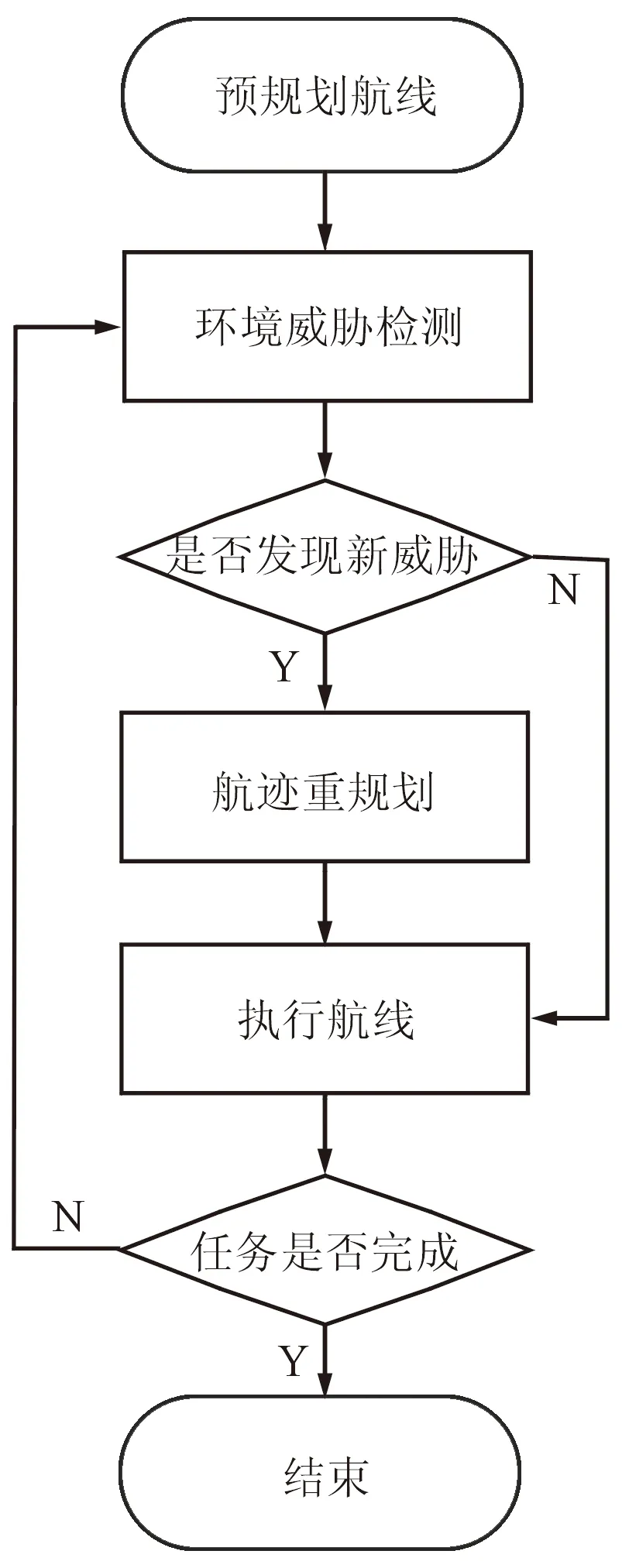
图1 算法流程Fig.1 Flow chart of algorithm
2 算法实现
2.1 ESDF地图
进入21世纪,ESDF被用于从传感器中过滤嘈杂的数据,并构建对象[12],而Ratliff等[5]带来了新的思路,将ESDF用于机器人的运动规划。ESDF在运用初期,不适用于增量构建,而在四旋翼无人机飞行过程中,需要不断对场进行动态更新。为此,Han等[13]提出增量ESDF生成方式,实现并验证了ESDF的动态更新。
ESDF源于TSDF(Truncated Signed Distance Functions),TSDF对距离信息进行了截断,即远离障碍物曲面一定距离后,视为无限大。这样的处理方式导致路径信息在穿过无限大的区域时,无法获取梯度信息。当控制点在障碍物里面时,无法被排斥出来。ESDF不对距离信息进行截断,可以很方便地对当前位置到障碍物表面的距离和梯度信息进行查询。采用开源工具FIESTA的原理[13],可以快速生成并动态更新ESDF地图。其流程如图2所示。
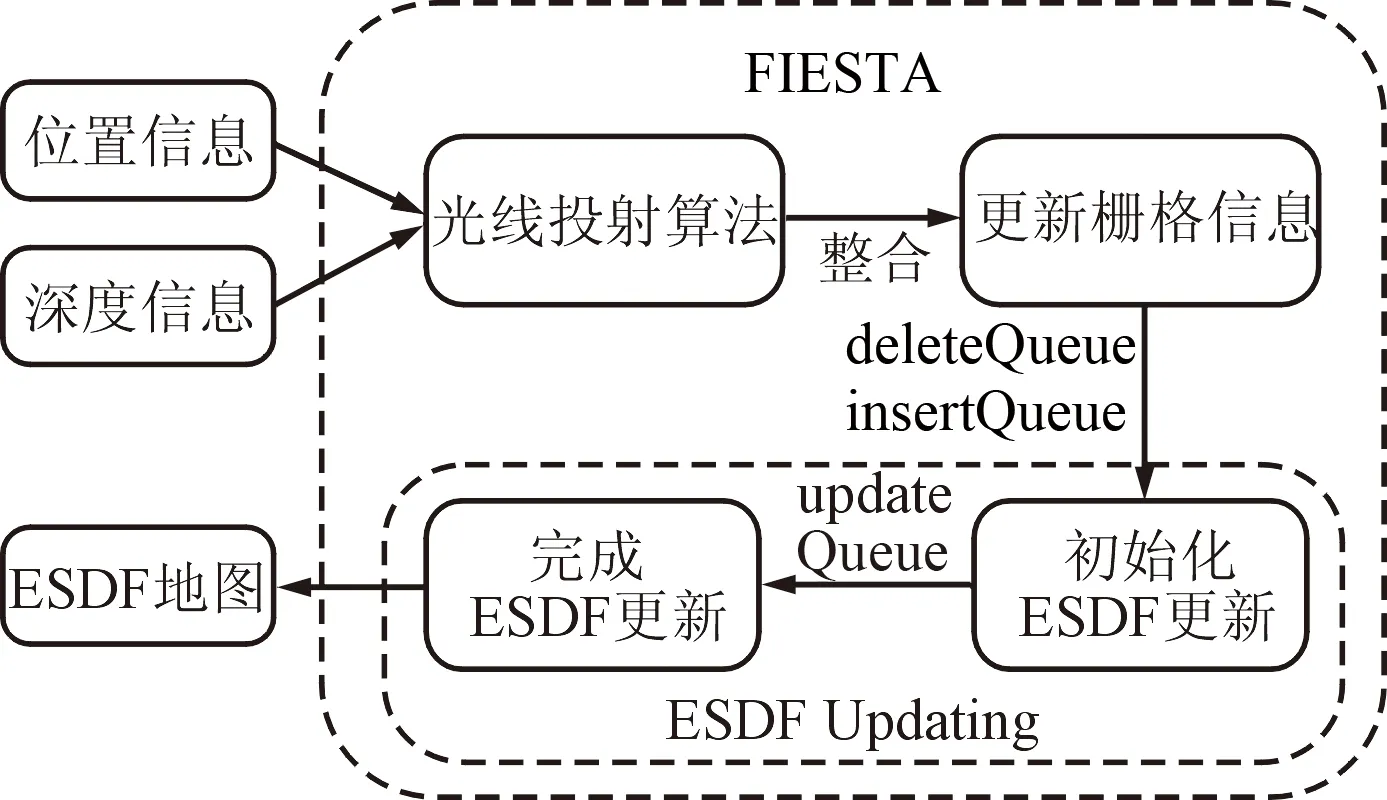
图2 FIESTA流程Fig.2 Flow chart of FIESTA
第一步,由传感器获取周围环境的位置信息和深度信息。
第二步,使用光线追踪法将点云叠加到占有的栅格地图中,然后将所有占用状态发生改变的体素分别添加到insertQueue和deleteQueue两个队列中。
第三步,初始化ESDF,将前2个队列合并到updateQueue队列中,并使用基于广度优先搜索算法的ESDF更新算法更新所有可能更改的体素。
2.2 B样条曲线
传统寻路算法如A*算法等,在生成路径时,部分路径段存在尖锐拐点。为了保障无人机飞行的安全性,采用B样条曲线进行路径优化可获得平滑路径[14]。B样条曲线的核心在于节点的划分,在无人机的路径规划中,B样条曲线的节点就是一个个的控制点Q。控制点作为决策变量,影响一段曲线的形状。B样条曲线的数学表达式如下:
(1)
式中,Ni,k(x)是k次B样条基函数,又称调和函数,是一个递归函数。其递归表达式如下:
(2)
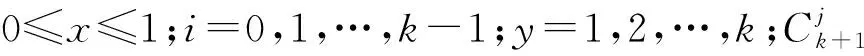
(3)
Dk=(x+k-i-y)k。
(4)
路径规划过程中,先生成初始控制点,并通过迭代的方式检测路径信息,对于迭代中检测到的每个碰撞段,生成无碰撞路径Г。之后,每个控制点Qi将在障碍物表面上分配一个锚定点Pij,并具有相应的排斥方向向量vij,如图3所示。
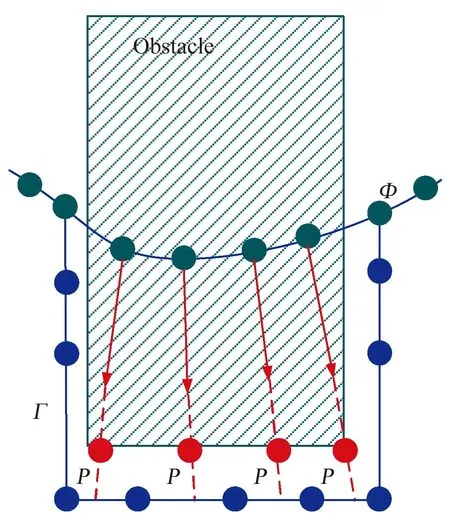
图3 控制点与锚定点Fig.3 Control points and anchor points
图中,i为控制点的个数,j为锚定点的个数,每一个锚定点和它的方向向量组合成一个(P,v)对,一个(P,v)对只对应一个控制点Qi。一个控制点到第j个锚定点的距离,即控制点到障碍物表面的距离可定义为dij,计算如下:
dij=(Qi-Pij)·vij。
(5)
2.3 飞行约束方程
为了将环境信息融入路径规划中,需要构造一个目标函数,即飞行约束方程,使轨迹可以远离障碍物。为了提高轨迹评估效率,算法中使用的B样条曲线,每一个控制点的时间间隔(Δt)是相同的。约束方程参照Faster-planner中对于四旋翼无人机局部路径规划的框架[13],每个控制点的速度Vi,加速度Ai和加加速度Ji表示如下:
(6)
参考文献[15],将控制点的优化问题抽象为:
(7)
式中,Js表示平滑惩罚项;Jc表示碰撞惩罚项;Jd表示可行性惩罚项;γ表示各惩罚项的权值。
2.3.1 平滑惩罚项
平滑惩罚项用于控制无人机的加速度,保障无人机在飞行过程中不会出现急加速。受益于B样条曲线的凸包性,最小化控制点的加速度及加加速度,就可以最小化曲线的高阶导数,使整条曲线更加平滑,因此,平滑惩罚项的可表示为:
(8)
式中,N表示控制点的个数。
2.3.2 碰撞惩罚项
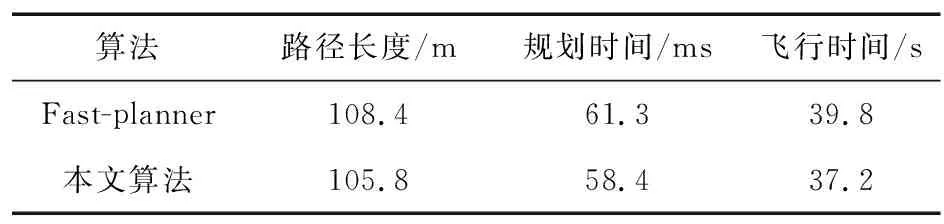
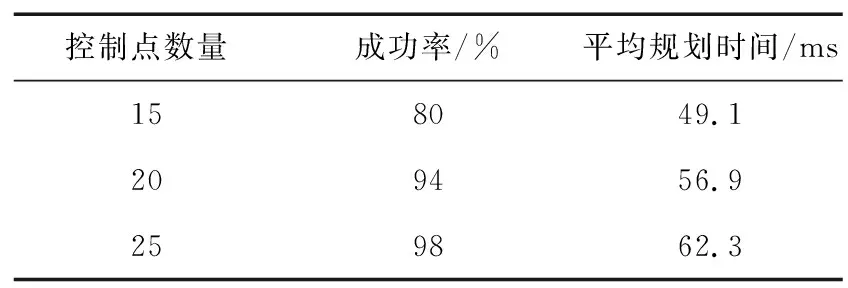
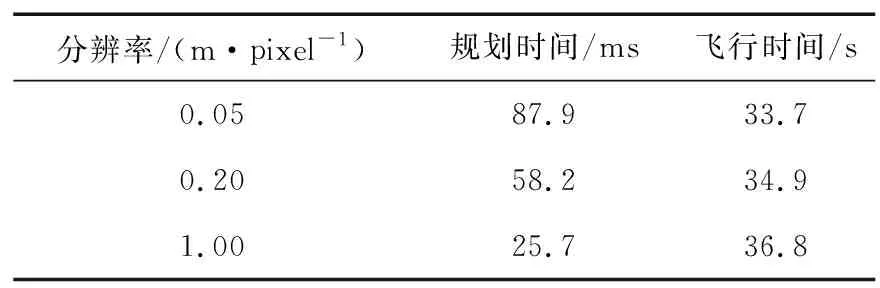
碰撞惩罚项用于将控制点通过场的作用推出障碍物。通过定义一个安全通道Sf,将控制点中dij (9) 由于每一个控制点单独计算碰撞惩罚项,曲线上整体的碰撞惩罚项的计算如下: (10) 2.3.3 可行性惩罚项 为确保轨迹的可行性,需要在曲线的每个维度上限制其高阶导数,即确保Vi,Ai和Ji都是可计算且有意义的。由于B样条曲线的凸包性,约束每一个控制点的导数,即可约束整条曲线。则可行性惩罚项Jd可表示如下: (11) 式中,w为相应的权值;函数F()是控制点的二次连续可微度量函数: (12) f(cr)的计算为分段函数: (13) 式中,cr∈C∈{Vi,Ai,Ji};a1,b1,c1,a2,b2,c2用来满足函数二阶连续性;cm为导数限制;cj为二次和三次函数的交界;λ<1-ε(ε≪1)为弹性系数,使得最终的结果满足约束。 目标函数J在飞行过程中自适应地根据新发现的障碍物进行改变,这个过程就是动态重规划。动态重规划中,时间间隔是一个关键变量,但在优化之前分配一个精确的时间间隔是不合理的,因为在初始化时不知道关于最终轨迹的信息。因此,额外的时间重新分配策略对于确保动态可行性至关重要。文献[16]将轨迹参数化为非均匀B样条曲线,并在某些线段超过导数极限时,迭代地延长属于一个时间间隔的控制点子集。 然而,时间间隔会影响多个控制点,且在开始状态附近调整时间间隔时,会导致前一段轨迹的高阶不连续性。使用各向异性曲线拟合方法[17],根据约束方程计算生成安全轨迹Φs。通过合理的时间重新分配,重新生成均匀的B样条轨迹Φf,使Φf自由优化其控制点,以满足高阶导数约束,同时保持与Φs几乎相同的形状。 需要比较控制点在改变后的变化情况,计算超过限制的比例re,即相比于Φs,Φf需要多分配多少时间。re的计算如下: (14) 式中,i∈{1,2,…,N-1};j∈{1,2,…,N-2};k∈{1,2,…,N-3};r∈{x,y,z};Vi,Aj,Jk分别与Δt的一次,二次,三次成反比。计算出re后,就可以计算出属于Φf的新的时间间隔Δt′: Δt′=reΔt。 (15) 控制点通过椭球度量(Spheroidal Metric)进行移动,该方法借助椭圆的性质来使同一球体表面的位移产生相同的惩罚,保障控制点移动过后,生成的Φf依然符合飞行约束。为了实现控制点的移动,需要建立模型Jf来表示从Φf到Φs的各项异性位移的积分。将Φf和Φs分别细化为αT′和αT(T′和T分别为轨迹Φf和Φs的时长,α∈[0,1]),由于初始曲线Φs已经符合飞行约束方程,实现了无碰撞,因此,对于需要生成的新曲线,使用带有低权重的轴向位移da来放宽光滑调整限制,用高权重的径向位移dr来防止碰撞。时间再分配示意如图4所示。 图4 时间再分配示意Fig.4 Schematic diagram of time reallocation (16) 由椭圆体的长半轴a和短半轴b计算轴向位移da和径向位移dr的积分,获得Jf: (17) 用新的Jf代替原目标函数中的Jc,实现了动态规划过程中的时间再分配,对原目标函数的实时性进行优化。 在Ubuntu20.04环境下的ROS系统中,使用Gazebo进行环境仿真,并在Rviz平台上展示路径规划过程。实验对比了在不同环境下不同路径规划算法的性能,并针对算法中的个别参数,进行对比实验。通过实验,分析算法的可行性和实用性。 在简单的环境中,设置了数量较少的障碍物,地图大小为20 m×20 m×5 m,设置统一的起点和终点,设置无人机的最大飞行速度为3 m/s,采用不同的算法进行实验。实验飞行轨迹如图5所示。由图5可以看出,动态规划的路径与传统的A*算法在路径规划上有很大区别。相较于A*算法,采用了B样条曲线的方法,规划的路径更为平滑,能更好地适应无人机的动力控制。 图5 简单环境飞行轨迹Fig.5 Flight path in simple environment 实验记录了采用不同算法时无人机的飞行轨迹长度、规划时间和飞行时间,如表1所示。由表1可以看出,传统的A*算法[18]在路径规划的计算速度上有很大的优势,且能找到最短飞行路径。本文算法性能上与Fast-planner[13]相当,但相比于Fast-planner,可以找到更短一些的路径。 表1 算法对比Tab.1 Comparison of algorithm 为了更直观地比较飞行过程中无人机状态的区别,记录了采用不同算法时,无人机飞行过程中的速度,如图6所示。可以看出,采用A*算法时,无人机的速度波动较大,Fast-planner和本文算法能更好地控制无人机匀速飞行。 图6 无人机速度变化对比 Fig.6 Comparison of UAV speed changes 将地图扩大,变为50 m×50 m×5 m的大地图,且在地图中随机生成200个障碍物,其中存在少量速度为0.5 m/s做巡回运动的动态障碍物。对采用动态规划思想的2种算法进行对比,飞行轨迹如图7所示。 图7 复杂环境飞行轨迹Fig.7 Flight path in complex environment 无人机在规避动态障碍物时的路径改变如图8所示,图中绿色方块为移动中的障碍物,图片中的曲线变化展示了无人机在遇到动态障碍物时,根据约束方程进行避障的过程。 图8 动态避障轨迹变化Fig.8 Trajectory change for dynamic obstacle avoidance 与前面的实验相同,记录飞行的路径长度与时间等信息,动态规划算法对比如表2所示。由表2可以看出,本文算法在复杂环境下仍能快速找到合适的路径,且寻路能力相较于Fast-planner有所提升。在面对动态障碍物时,也能及时改变飞行轨迹,实现动态避障。 表2 动态规划算法对比Tab.2 Comparison of dynamic planning algorithms 针对控制点的个数对飞行质量的影响,在复杂地图中随机选取起点和终点位置,就控制点数量,各进行50次实验,记录实验的成功率和平均规划时间,如表3所示。针对ESDF地图分辨率对算法的影响,做同类型对比实验,改变地图分辨率,以相同的起点和终点进行飞行,记录飞行时间和规划时间,实验结果如表4所示。 表3 控制点数量对比Tab.3 Comparison of number of control points 表4 地图分辨率对比Tab.4 Comparison of map resolution 由表3可以看出,控制点的数量会影响飞行的成功率,控制点越多,说明提前规划的路线越长,越能提前找到合适的路径,但规划所需的时间也随之增长。地图分辨率对于算法的影响在于规划时间上的区别。由表4可以看出,高分辨率的情况下,需要更长的时间进行规划,但能找到更贴近障碍物安全面的路径,减少路径上的消耗。 本文提出的B样条曲线结合时间再分配的无人机动态避障算法,可以做到根据无人机飞行过程中动态生成的ESDF地图,迅速规划一条平滑、安全的路径。该路径中各控制点均符合无人机的动力学模型,有利于无人机的飞行控制。 基于Gazebo和Rviz的模拟仿真环境的实验,验证了算法的有效性。在面对外界干扰如动态障碍物时,算法依然保证了无人机选择合理的路径。算法具有良好的实时性,拥有广泛的应用前景。 本文提出的方法,依赖于ESDF地图,在地图的构建中消耗了大量计算时间,如何提高计算速度,减少对ESDF地图的依赖,是后续研究的方向。2.4 时间再分配策略


3 算法实验
3.1 在简单环境下的实验对比
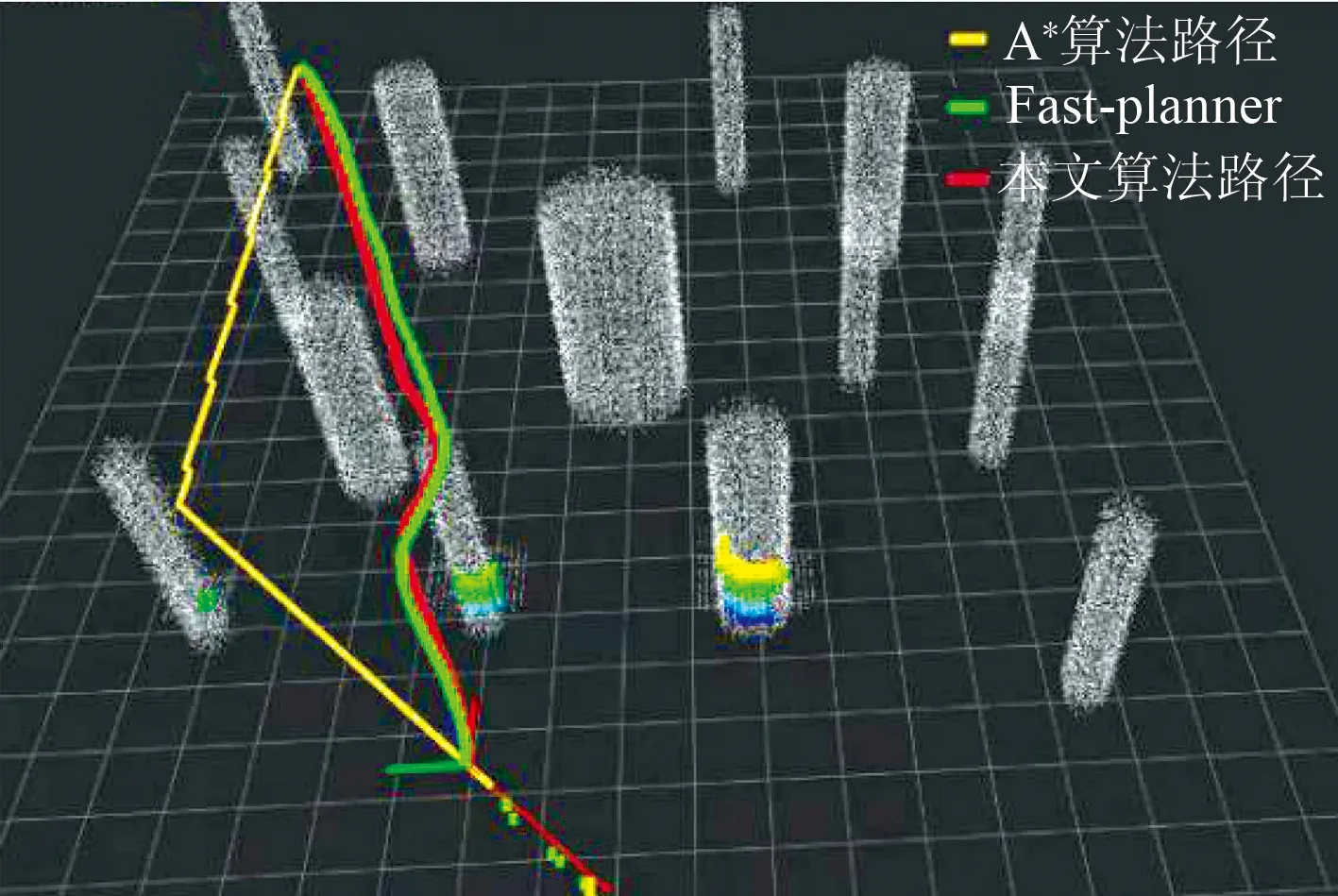
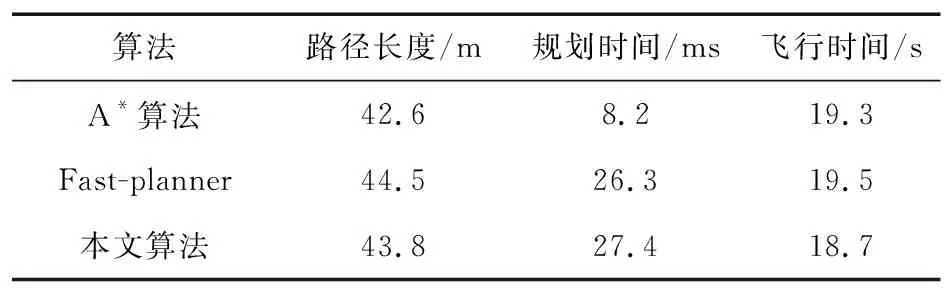
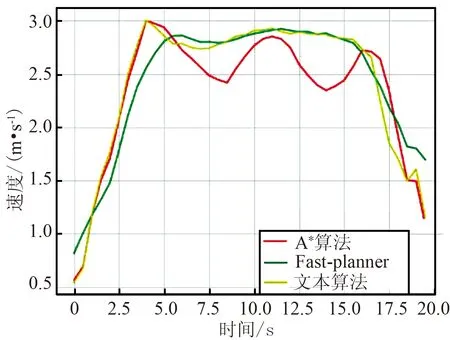
3.2 在复杂环境下的实验对比

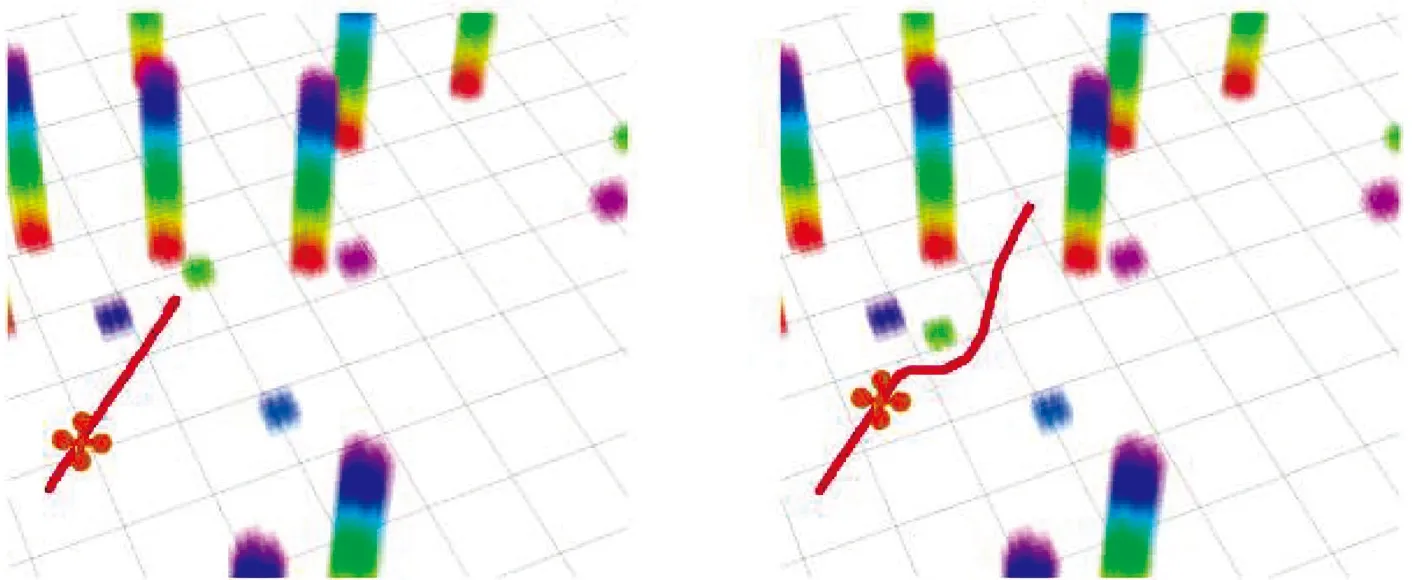
4 结束语
