数据驱动的双通道CNN-LSTM调制分类算法

葛 战,孙 磊,李 兵,蒋鸿宇,周 劼

(中国工程物理研究院 电子工程研究所，四川 绵阳 621900)

0 引言

通信信号的调制分类是指能够在具有极少先验信息的情况下正确确定目标信号的调制类型，在各领域均有相当大的应用需求[1]，作为信号盲处理相关领域的重要研究内容，仍有许多问题亟待研究[2]。近年来，深度学习方法由于其在图像识别等领域表现出的优异性能，被引入到调制分类这一问题的研究当中[3-4]。

基于深度学习的调制分类方法能够直接对信号进行学习，与传统基于信号特征的方法(如瞬时特征[5]、高阶累积量[6]以及循环谱等[7])相比，无需人工提取分类特征，减少了信号预处理步骤，具有一定的应用优势。文献[8]首先提出采用二维卷积神经网络(Convolutional Neural Network，CNN)直接从时域数据中学习信号的调制类型，但识别结果不甚理想。文献[9]采用一维CNN实现信号的分类，与二维CNN相比有效降低了训练时间。文献[10-11]采用长短时记忆(Long Short-Term Memory，LSTM)网络对时域数据进行训练实现调制分类，有效提升了识别率，但训练时间相对较长，同时文中考虑的信号长度仅为128，若信号过长会造成LSTM网络出现梯度消失等问题。

1 信号模型及信号表示

1.1 信号模型

假设接收信号已经经过预处理、匹配滤波等步骤，其解析形式可表示如下：

r(n)=αe-j(2πf0+θ0)x(n)+ω(n)，

(1)

式中，r(n)为接收符号；x(n)为发送符号，来自某一调制样式，假设服从独立同分布并进行了能量归一化；ω(n)是功率为σ2的加性高斯白噪声；α，f0和θ0为信号的幅度、频率估计误差和相位估计误差。

1.2 信号表示

由于深度神经网络一般需采用实值作为输入，而接收信号经过预处理后为复序列数据。因此，在采用深度神经网络直接从接收数据中学习时，首先需要确定合适的数据表示形式，以满足网络对输入数据格式的要求。根据复序列数据的特点，可以把接收信号分解为由实部(I路)和虚部(Q路)组成的实序列。

假设一个符号周期内的接收信号为r(k)=[r(1),r(2), …,r(N)]，其实部和虚部分别表示为R(r(k))和I(r(k))。按照上述描述可以将r(k)表示为N×2维(N为信号长度)的矩阵数据(IQ数据)作为深度神经网络的输入，即：

(2)

2 算法设计

2.1 CNN-LSTM模型

提出的用于调制分类的CNN-LSTM模型结构如图1所示。模型主要由输入数据、CNN模块、LSTM模块以及分类模块组成。

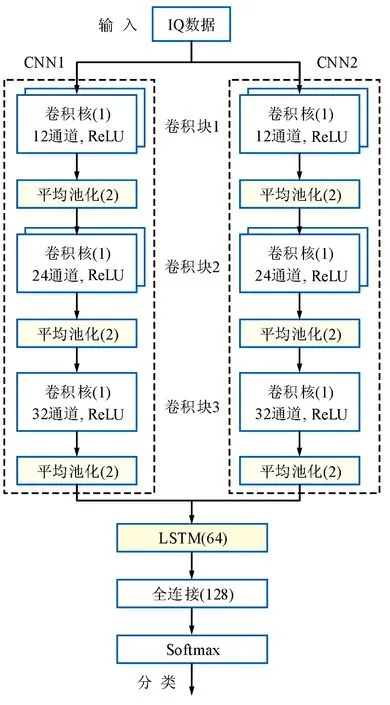
图1 提出的CNN-LSTM模型结构Fig.1 Proposed CNN-LSTM network structure

输入数据：信号被转换为由实部(I路)和虚部(Q路)组成的实序列，即IQ数据，表示形式为N×2，然后被送入至CNN模块。

CNN模块：用于提取信号的空间特征信息[13]。模块由2个CNN子模块组成，每个子模块均由3组一维卷积层和3个池化层串联组成。图1中卷积块1～3的通道数依次为64，32和24，卷积核大小均为1，激活函数为ReLU。池化层采用大小为2的平均池化，用于进一步缩减网络参数。

从研究进程来看 我国深度学习的真正研究始于2005年，2010年后相关研究日渐增多，2013—2017年一直保持逐年增长的研究态势。随着国内外深度学习的专注度及学习科学的发展，从近几年的研究成果可以看出，国内深度学习研究从初期关于学习概念、内涵的技术研究，到目前实践与应用研究，研究主题呈现本土化，包括基于翻转课堂、移动教学、MOOC、SPOC等个案探索实验，均体现了深度学习在国内的持续发展。

模型中2个CNN模块采用相同的参数，其中卷积操作和池化过程为[9]：

(3)

(4)

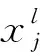
2个CNN模块同时从输入IQ数据中各自提取空间特征信息，经过融合后被送入LSTM模块。

LSTM模块：用于提取信号的时序特征信息[14]。LSTM网络中采用存储单元代替常规神经网络中的神经元，每个存储单元通常由多个记忆细胞ot和3个控制门组成(分别为输入门it、遗忘门ft和输出门ot)[15]。本文采用一层LSTM网络从双通道CNN模块提取的空间信息中进一步提取时序信息，有效利用了2种网络的各自优势。LSTM网络各状态的更新过程为[16]：

(5)

式中，wi，wf，wo和bi，bf，bo分别表示输入门、遗忘门和输出门的权重和偏置；σ为Sigmoid激活函数。

分类模块：采用单层全连接层实现(神经元为128)，以Softmax作为激活函数，通过对整个网络训练得到调制分类结果。

2.2 训练过程

实验中网络结构由TensorFlow2.4深度学习框架搭建，优化器为ADAM。训练过程中会将分类器的输出与样本对应的标签信息进行比较，采用反向传播法迭代更新网络参数以使得损失函数最小，其中损失函数由交叉熵确定：

(6)

式中，m，j，k分别为样本数量、样本标签以及调制种类；q(·)为指示函数；lnp(·)为样本zi的概率。

模型训练的初始学习率、批处理大小和迭代次数分别设置为0.001，100和50。训练中采取变更学习率和提前终止策略，当网络模型在验证集上的损失变化连续5个epoch小于0.001时学习率缩减10倍，连续10个epoch小于0.001时则停止训练，上述策略有助于提升训练精度并减少训练时间。

3 算法仿真及分析

3.1 数据集构建

采用深度神经网络解决分类问题时，需要产生训练所需的训练样本、验证样本和测试样本。其中，训练样本和验证样本用于模型的训练和验证，测试样本用于模型训练完毕后分类性能的测试。本次仿真共产生5种经过标注的信号(BPSK，QPSK，8PSK，16QAM，64QAM)。信噪比为0～20 dB，每种信号每隔1 dB产生1 000个样本，其中800个样本用于训练，200个样本用于验证。信号样本标签采用one-hot编码格式。测试样本按照上述形式单独产生，每种调制样式每隔2 dB产生600个测试样本。

3.2 整体性能分析

对提出的调制分类算法进行仿真实验，假设信号频偏和相偏已被准确估计，但信噪比未知。信号长度分别为128，256和512，实验结果如图2所示。可以看出，随着信号长度的增加，识别率也在提升。在0～20 dB,3种不同信号长度对应的平均识别率依次为84.6%，86.3%和88.3%，表明信号长度的增加有助于神经网络特征的提取。

信号长度为128时，各信号的识别率如图3所示。可以看出，BPSK和QPSK在低信噪比时仍具有较优的识别性能，即使0 dB时BPSK的性能依然为100%，而QPSK在4 dB时也能够接近100%。此外，在低信噪比时，64QAM相比16QAM得到了较高的识别性能，说明本文提出的算法能够从64QAM中学习到更加明显的分类信息。

图3 各信号的识别性能Fig.3 Classification performance of each signal

3.3 存在估计误差时的性能分析

考虑到实际信号预处理过程中可能存在相位偏移和频率偏移等估计误差，将验证该条件下提出算法的识别性能。设信号的信噪比为4 dB，相偏为-20°～20°，频偏为0～3×10-4。重新生成测试集，其中相偏的间隔为5°，频偏的间隔为5×10-5。采用3.2节中已训练完成的模型对存在估计误差的测试样本进行测试。图4和图5分别为存在相偏和频偏时不同信号长度的识别性能。

图4和图5中，相偏在-10°～10°及频偏小于1×10-4时，识别性能所受影响不大，说明提出的深度神经网络算法对相位和频率偏移有一定的冗余度。图4中随着相偏的继续增加，识别性能开始大幅下降，此时模型对信号估计误差的适应能力逐渐变差。图5中随着信号长度的增加对频偏的容忍度则越差，主要是由于信号长度的增加使得信号旋转更为明显，造成识别困难。

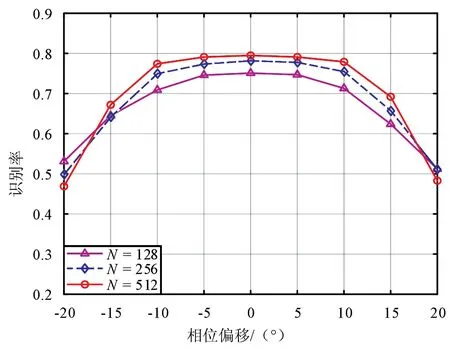
图4 存在相偏时的识别性能Fig.4 Classification performance in the presence of phase offset

3.4 不同深度神经网络的性能分析

将提出的算法(采用C-L表示)与现有几种深度神经网络方法进行对比。文中C-L模型为了同时利用CNN与LSTM分别在空间和时序上的特征提取能力，采用了由双通道一维CNN和LSTM相互串联的形式，因此一个比较直观的想法是，验证所提出模型与模型组成中的CNN和LSTM相比有多少性能的提升。同样，文献[17]为了利用2种网络的各自优势，提出了一种由CNN和LSTM相互并联的结构实现调制分类，本节也将其引入进行性能对比。综上，将提出的C-L方法与图1中的CNN子模块、LSTM以及二者并联的方法(采用C&L表示)进行对比，3种模型中CNN和LSTM的参数与C-L模型一致。

4种网络结构在0～20 dB的平均识别率如表1所示。从表1可以看出，C-L在识别性能上优于其他几种深度神经网络方法。由此可见，采用CNN和LSTM串联的网络结构相比单独采用CNN或LSTM，能够同时利用二者的特征提取能力，有效提升了调制分类的性能，而同样采用二者相结合的并联结构(C&L)性能上则相对较差。

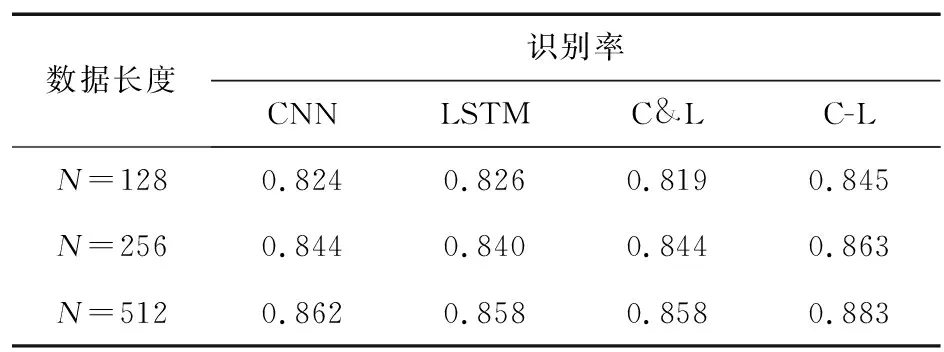
表1 不同深度神经网络的平均识别率Tab.1 Average classification performance of different deep neural networks

表2列举了4种网络模型的计算复杂度，包括模型的参数量、浮点计算次数以及迭代时间。从表2可以看出，由双通道CNN和LSTM组成的C-L模型在参数量和浮点计算次数上均小于单独的CNN模型，但迭代时间相对较高。主要原因是C-L模型中CNN提取出的空间特征会被送入至参数较少的LSTM，相比较直接送入全连接网络减少了网络连接数量，但双通道CNN结构以及LSTM均会使得迭代时间有所增加。同时可以得到，与同样采用2种网络相结合的C&L并联结构相比，C-L串联结构不仅具有识别性能上的优势，同时还具有计算复杂度上的优势。

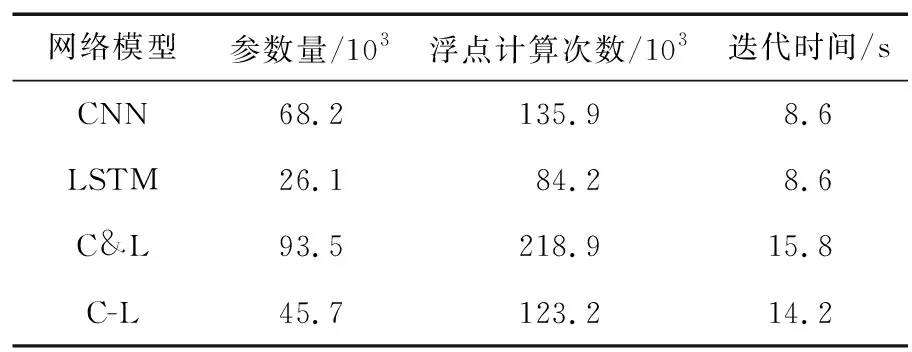
表2 不同深度神经网络的计算复杂度Tab.2 Computational complexity of different deep neural networks

3.5 网络参数对识别性能的影响

本节验证了深度模型的网络参数对识别性能的影响。现有文献采用一维CNN对IQ数据进行学习时，常采用的卷积核大小为3[9]，本文根据IQ数据的特点(其形式为N×2)，采用大小为1的卷积核，这样每个卷积核会与每个数据执行卷积操作，达到提取输入数据完整信息的目的。同时与单通道CNN-LSTM结构进行比较，验证了双通道的有效性。基于上述描述，得到了4种具有不同参数的网络模型，其实验结果如表3所示，其中“C1-L-k3”表示单通道，卷积核大小为3，“C2-L-k3”表示双通道，卷积核大小为3，其他2种表示以此类推。

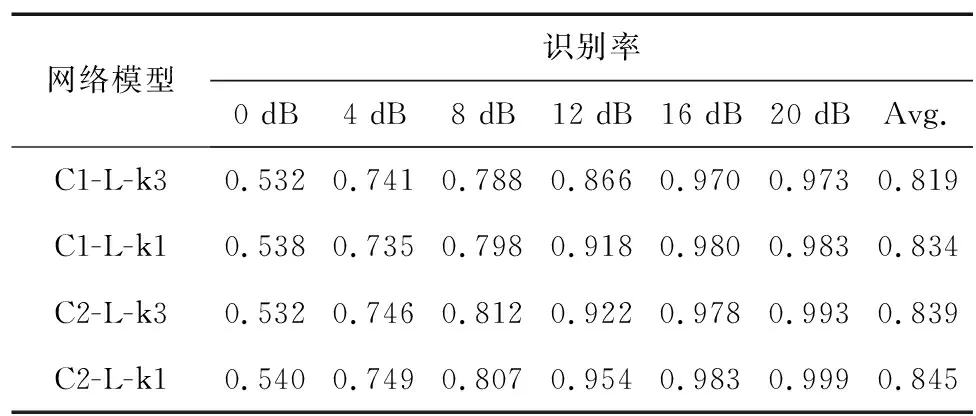
表3 网络参数对识别率的影响(N=128)Tab.3 Influence of network parameters on classification performance (N=128)

由表3可以看出，双通道结构的识别性能优于单通道结构，表明2路CNN组成的双通道结构能够提取出更多不同的特征信息，有助于分类。卷积核大小为1时优于大小为3时，其中双通道结构性能提升0.6%，单通道提升1.5%。实验结果表明，本文提出的方法能够有效改善调制分类性能。

3.6 与传统方法性能对比

为进一步验证C-L方法的分类性能，将其与现有的传统方法进行比较。文献[18]给出了理想环境下信号调制样式分类的理论极限，称为极大似然方法(记为“ML”)，常作为其他方法的比较标准。文献[19]采用模糊C均值聚类算法和全连接神经网络实现了对5种信号进行分类(记为“FCM”)。本节实现了上述2种方法，同时参照文献[6]采用4阶和6阶累积量以及全连接神经网络实现了对本文调制样式的分类(记为“CUM”)。信号长度为512，信噪比未知时，4种方法的识别性能如图6所示。

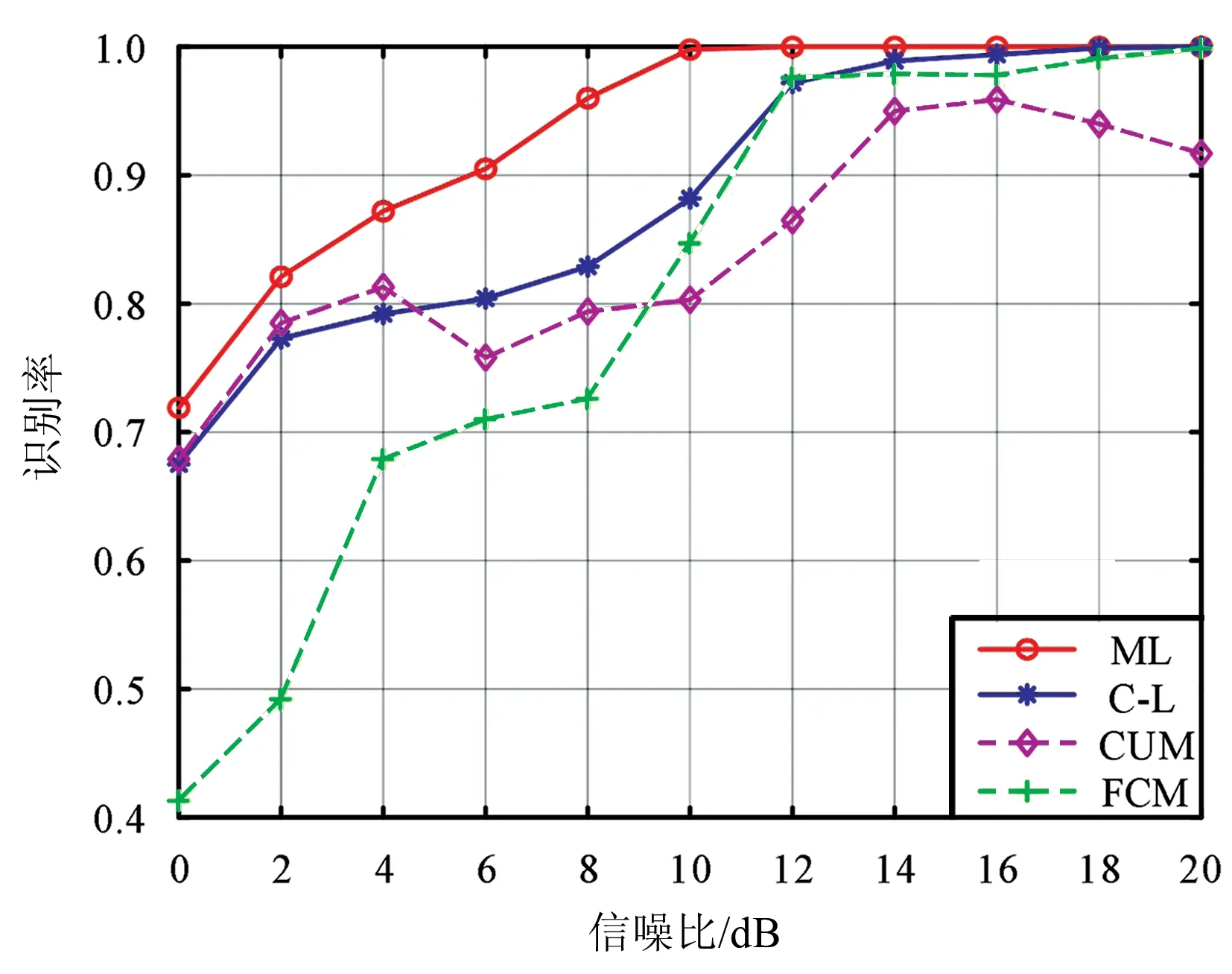
图6 信噪比未知时不同方法的性能对比(N=512)Fig.6 Performance comparison of different methods when SNR is unknown (N=512)

从图6可以看出，ML方法性能最优，C-L方法在低信噪比时性能略低于CUM方法，随着信噪比的增加，性能逐渐提升。FMC方法在低信噪比时性能最差，当信噪比大于10 dB时优于CUM方法。经计算，4种方法的平均识别率分别为93.4%，88.3%，84.2%和79.9%(依次为ML，C-L，CUM和FCM)。

为测试信噪比对分类性能的影响，把信号样本对应的信噪比引入至所提出的模型。由于信噪比为标量数据，不宜直接送入至神经网络进行训练。因此，首先把信噪比送入至单层全连接层(神经元为10)进行编码，然后再与图1中2个CNN子模块的输出相融合，最后再送入LSTM进行分类。实验结果如图7所示。由图7可以看出，C-L方法在性能上接近ML方法，整体优于FCM和CUM方法，但在低信噪比时CUM会得到较好的性能，因此后续应考虑将2个特征相结合的识别方法。经计算，4种方法的平均识别率分别为93.4%，92.4%，90.8%和86.5%(依次为ML，C-L，CUM和FCM)。与上一实验对比可得，信噪比有助于调制样式的分类，因此实际中应该尽可能估计出信噪比。

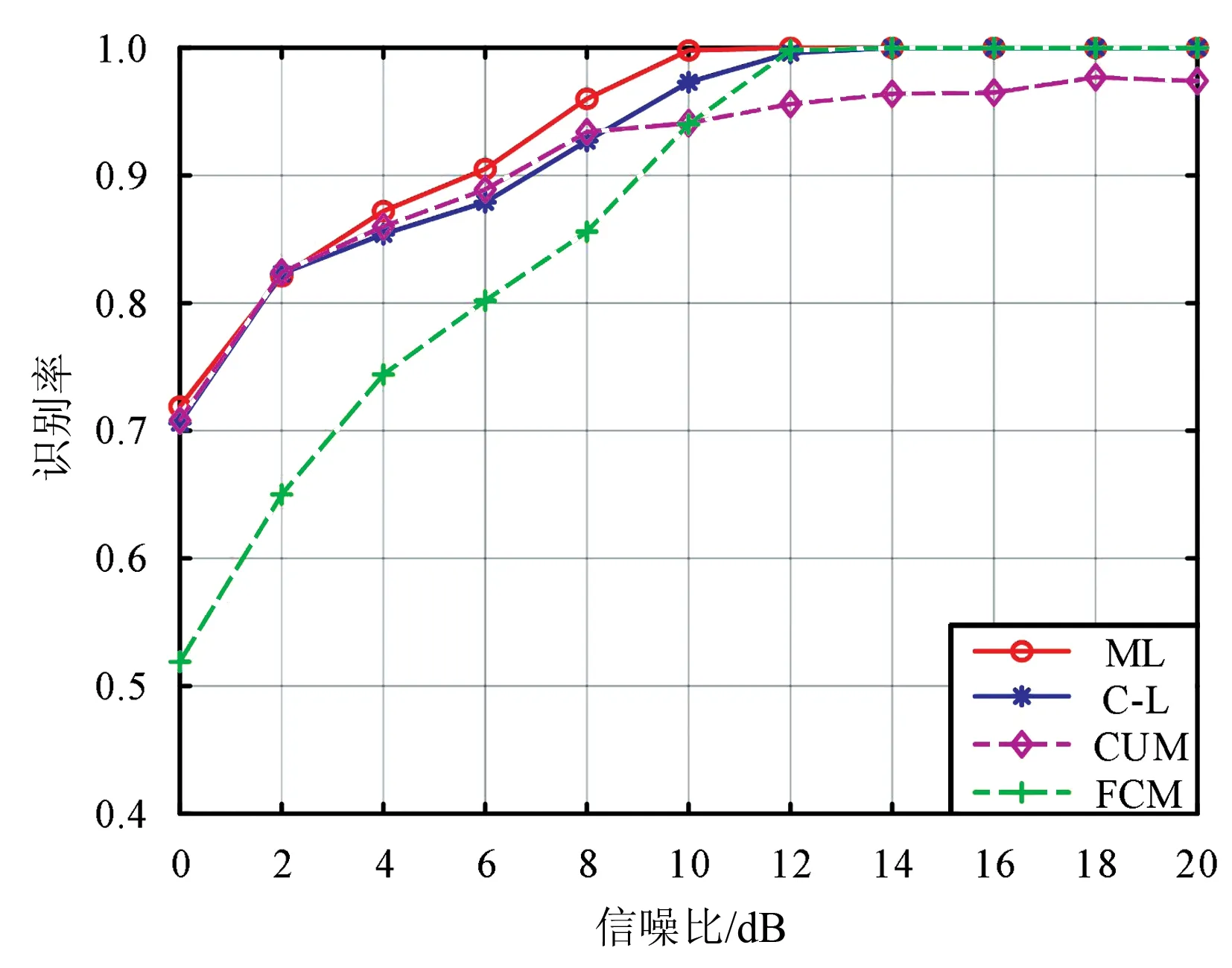
图7 信噪比已知时不同方法的性能对比(N=512)Fig.7 Performance comparison of different methods when SNR is known (N=512)

4 结束语

本文采用数据驱动的方式直接以信号的时域数据作为深度神经网络的输入实现了对5种调制信号的分类。提出了一种基于双通道一维CNN和LSTM相互串联的网络结构，同时利用CNN在空间上以及LSTM在时序上2个不同维度的特征提取能力进行联合学习。实验结果表明，CNN与LSTM相互串联的网络结构更加有利于特征信息的提取，相比较单独采用CNN，LSTM以及二者之间的并联结构，在识别性能上均有一定的提高；采用双通道CNN模块以及减小卷积核大小的操作更有利于特征信息的挖掘。此外，通过和传统基于高阶累积量以及聚类特征的方法相比，提出的方法无需人工提取分类特征且性能上也有较大的优势。