Rashba 自旋-轨道耦合调制的单层半导体纳米结构中电子的自旋极化效应*
2023-02-18贺亚萍陈明霞潘杰锋李冬林港钧黄新红
贺亚萍 陈明霞 潘杰锋 李冬 林港钧 黄新红
(桂林理工大学,桂林 541004)
利用现代材料生长技术纳米厚的半导体可以沿着良好的方向有序生长,形成层状半导体纳米结构.在这种半导体纳米结构中由于结构反演对称性破缺出现较强的自旋-轨道耦合,能有效消除半导体中电子的自旋简并,导致电子自旋极化效应,在自旋电子学领域中具有重要的应用.本文从理论上研究了单层半导体纳米结构中由Rashba 型自旋-轨道耦合引起的电子自旋极化效应.由于Rashba 型自旋-轨道耦合,相当强的电子自旋极化效应出现在该单层半导体纳米结构中.自旋极化率与电子的能量和平面内波矢有关,尤其是其可通过外加电场或半导体层厚度进行调控.因此,该单层半导体纳米结构可作为半导体自旋电子器件应用中的可控电子自旋过滤器.
1 引言
分子束外延生长[1]和金属有机化学气相沉积[2]等现代材料生长技术能使纳米厚半导体沿着一个良好的方向有序生长,构筑所谓的层状半导体纳米结构(layered semiconductor nanostructure,LSN)[3].在一个LSN 中,半导体层的晶格匹配得很好,归因于现代先进的材料制备技术.特别是由于层状结构形式导致结构反演对称性的破缺,在LSN 中存在很强的自旋-轨道耦合(spin-orbit coupling,SOC),即电子的自旋和其动量之间的相互作用[4].一般有两种机制不同的SOC 效应: 一种为Rashba 型[5],由表面或界面处结构反演不对称所造成,而且可通过外加电场实现调控[6];另一种为Dresselhaus 型[7],由块体结构反演不对称引起,强度可由应力工程进行控制[8].这些重要的SOC 能有效地消除常规半导体中电子的自旋简并,诱发零场自旋劈裂,从而产生自旋极化效应[9].
近年来,在LSN 中由SOC 效应引起的电子自旋极化输运引起了大家越来越多的研究兴趣,因为其在半导体自旋电子学领域中具有潜在的应用,可作为一种优良的自旋极化源[10].通常Rashba 型SOC 固存于反对称的LSN 结构中,负责半导体中电子自旋极化的产生[11,12],但是,其自旋极化率可通过外加在不对称LSN 上的电场进行调控[13].在对称的LSN 中,仅存在Dresselhaus 型SOC 使半导体中电子产生自旋极化[14−19].不过,在对称LSN中沿着电子的输运方向施加外电场,也能在对称LSN 中引发Rashba 型SOC,从而使半导体中的电子发生自旋极化[20].在一般的LSN 中,同时存在Rashba 型和Dresselhaus 型两种SOC 效应,均可在半导体中引起电子的自旋极化效应,不过两者具有不相同的贡献[21−23].而且,LSN 中电子的自旋极化效应在共振时通常会更强,因为其满足更为苛刻的共振条件,即电子的能量严格等于LSN 中的束缚能[24,25].此外,当自旋极化电子隧穿通过LSN 时,在半导体层面内伴随出现电荷流;反之亦然.这种有趣的电荷-自旋转换现象,称为自旋流电效应[13,14,26].
最近,Cao 等[27−30]提出一个新的LSN: InSb/InxGa1–xAs/GaSb,并系统地研究了由Rashba 型和Dresselhaus 型SOC 效应在半导体中产生的电子自旋输运性质.他们不仅揭示了电子通过该LSN 的自旋极化规律[27,28],而且还研究了利用δ-掺杂技术对电子自旋极化效应的调控[29,30].在这些研究工作的激励下,我们采用理论分析和数值计算相结合的方法,研究单层半导体纳米结构(singlelayered semiconductor nanostructure,SLSN)中Rashba 型SOC 效应产生的电子自旋极化,揭示SLSN 中电子自旋极化输运的规律,提出基于SLSN 的电子自旋过滤器.因为Rashba 型SOC 效应,在SLSN 中出现了明显的电子自旋极化.自旋极化率的大小与极性可通过外加电场或半导体层厚度进行有效地调控.因此,SLSN 可作为半导体自旋电子学器件应用中的可控电子自旋过滤器.
2 模型与理论
如图1 所示,该SLSN-InSb 结构沿着z//[001]方向生长,坐标(x,y,z)分别平行于立方晶轴([100],[010],[001]),参量d和V分别表示半导体层的厚度和电子经历的等效势.采用单粒子、有效质量近似,电子在这个SLSN 中的哈密顿量为[27]
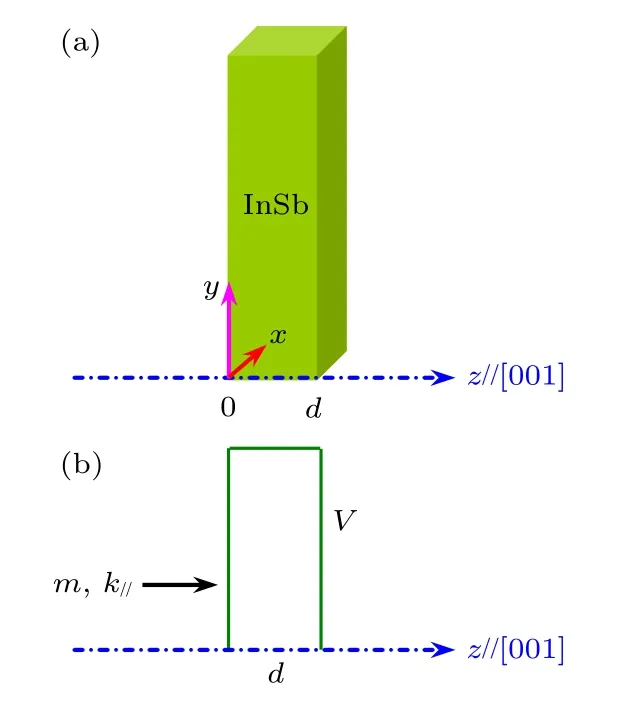
图1 (a) SLSN-InSb 结构沿 着z//[001]方向生 长;(b)用于理论分析与数值计算的结构模型Fig.1.(a) SLSN-InSb grows along the z//[001] direction;(b) the structural model used for theoretical analysis and numerical calculation.
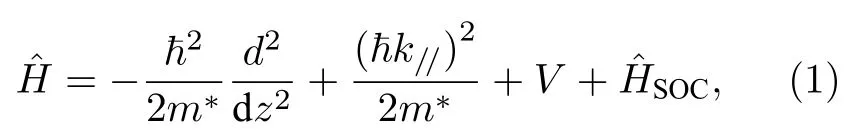
其中,m∗=αm,α,m,k//分别为电子在半导体InSb 中的有效质量、质量系数、真空中的自由质量与半导体层平面内的波矢(又称平面内波矢).这里应该注意的是,方程(1)中的哈密顿量是一个唯像近似,即在单电子、有效质量近似下,电子隧穿通过LSN 时半导体层通常可等效为一个势垒或势阱,而且本文的侧重点放在讨论半导体层的物理参数对电子自旋极化的影响.方程(1)等号右边最后一项是Rashba 型SOC 项,即这一项在表象中可以写为[29]
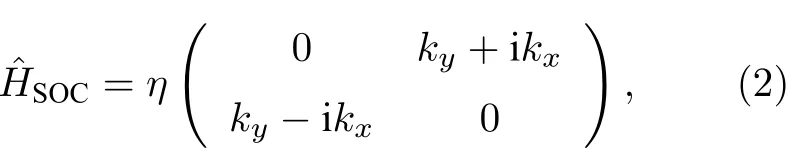
其中,η是Rashba 型SOC 的强度,可通过外加电场进行调制.在方程(1)和方程(2)中,已经假设直角坐标(x,y,z)分别平行于立方晶轴([100],[010],[001]).利用旋量Rashba 型SOC 项(2)式可被对角化为HSOC=σzηk//,其中ϕ=tan−1(kx/ky),以及σz=±1 分别对应于电子的自旋向上(+1)自旋向下态(–1).
因为电子在SLSN中半导体层xy平面内运动守恒,其波函数为其中r=(x,y)是层xy平面内的位置矢量,以及ψ(z)为电子波函数的z分量,且满足下面的一维Schrödinger 方程:
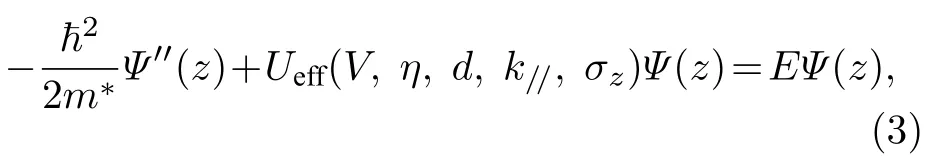
式中,能量为E的电子在SLSN-InSb 结构所感受到的有效势为
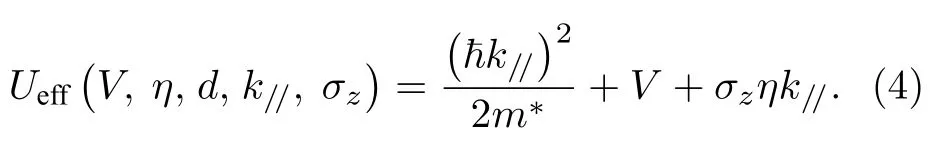
为了便于理论分析和数值计算,涉及的所有物理量都写成无量纲的形式,比如E→EE0和z→zℓ0等,其中E0和分别为长度和能量的单位,如果能量单位取为E0=0.1 eV,那么长度单位为ℓ0=0.86 nm.
利用转移矩阵方法[31,32],Schrödinger 方程即(3)式可以严格求解,从而计算自旋电子隧穿通过SLSN-InSb 结构的透射系数.不失一般性,电子在入射区和透射区的波函数可以分别假设为

根据透射系数,定义自旋极化率来表征电子通过SLSN 的自旋极化效应程度,其表达式为
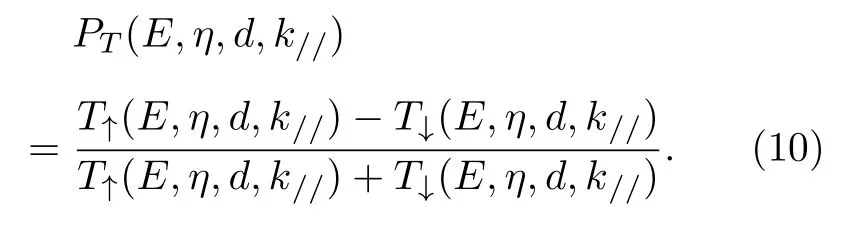
其中,T↑(E,η,d,k//) 和T↓(E,η,d,k//) 分别为自旋向上电子和自旋向下电子的透射系数.
3 结果与讨论
对于SLSN-InSb 结构(图1),其主要参数[33,34]为: 有效质量m*=0.0136 m,等效势V=0.32 eV,Rashba 型SOC 的强度η=0.012 eV·nm和半导体InSb 层的宽度d=8 nm.首先,研究电子通过该SLSN 结构的传输是否依赖于它的自旋,计算了自旋向上电子(上三角)和自旋向下电子(下三角)隧穿通过SLSN 结构的透射系数,电子在平面内的波矢取为k//=0.2 nm–1,结果见图2.与自旋向下电子比较,自旋向上电子的透射曲线向着高能区移动,因此自旋向上电子和自旋向下电子之间的传输存在明显不同,即电子隧穿通过SLSN-InSb 结构时,出现了明显的自旋劈裂现象——自旋极化效应.显然,这样一个依赖于自旋的传输源自于该SLSN-InSb 结构中较强的Rashba 型SOC 效应.电子穿过这个SLSN 结构的另外一个特征是当电子的能量刚好等于SLSN 结构内的束缚能级时,在透射谱上就会出现透射系数为1 的共振峰.
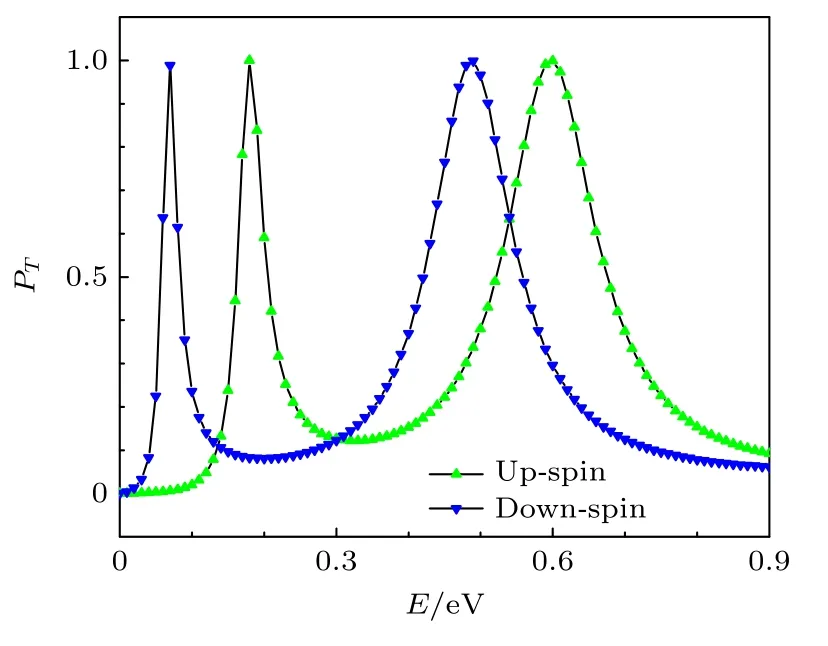
图2 平面内波矢为 k// =0.2 nm–1 的自旋向上电子和自旋向下电子隧穿通过 SLSN-InSb 结构(图1)的透射系数,其他参数为 V=0.32 eV,d=8 nm,η=0.012 eV·nmFig.2.Transmission coefficient for spin-up and spin-down electrons with in-plane wave vector k//=0.2 nm–1 tunneling through the SLSN-InSb (Fig.1),where other parameters are V=0.32 eV,d=8 nm,η=0.012 eV·nm.
图3 展示了电子通过SLSN-InSb 结构出现的自旋极化效应,给出了电子在平面内波矢分别为k//=0 (方形),0.1 (圆形),0.2 nm–1(三角形)时电子的自旋极化率,其他结构参数与图2 相同.由图3 知,当平面内的波矢k//=0 nm–1(即垂直入射)时,自旋极化率严格为0,其归因于与自旋无关的有效势,即方程(4).但是对于非零的平面内波矢,电子在SLSN 结构中的有效势就依赖于其自旋,结果导致相当大的电子自旋极化效应,如图3 圆形线和三角形线所示.而且,电子的自旋极化率明显关于平面内波矢各向异性的特点,这是因为电子在SLSN 结构中的有效势与平面内波矢相关.随着增大平面内的波矢,电子自旋极化效应一般会变强,而且自旋极化率曲线向着高能方向移动.由于这样一个相当强的自旋极化效应,该SLSN 结构可以作为半导体自旋电子学器件应用中的电子自旋过滤器.
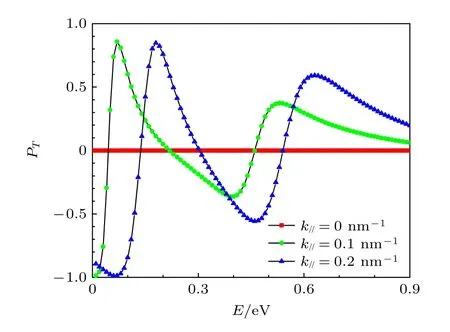
图3 平面内不同波矢的电子通过SLSN-InSb 结构(图1)时的自旋极化率,图中其他参数为 V=0.32 eV,d=8 nm,η=0.012 eV·nmFig.3.Spin polarization ratio for the electron with in-plane different wave vector across the SLSN-InSb (Fig.1),where other parameters are V=0.32 eV,d=8 nm,η=0.012 eV·nm.
从实际应用来看,半导体自旋电子学领域特别渴望得到可控的自旋过滤器[35].下面将研究基于SLSN-InSb 结构的电子自旋过滤器的可能操控,旨在获得可控的自旋极化源.图4 和图5 中仅仅考虑电子在平面内波矢为k//=0.2 nm–1的情况,是为了突出调控的原理.由于在SLSN 结构中,Rashba型SOC 效应的强度可通过应用外电场进行改变,因此首先研究Rashba 型SOC 强度对上述电子自旋过滤器的影响.在图4 中,作为电子能量的函数,展示了在给定Rashba 型SOC 强度分别为η=0.012(方形),0.096(圆形),0.192 eV·nm(三角形)时的自旋极化率,其中等效势V=0.32 eV 以及InSb 层厚度d=8 nm.当Rashba 型SOC 效应变强时,电子自旋极化率谱线快速向高能区移动,不过自旋极化率的幅度稍稍有所降低.因此,电子隧穿通过SLSN-InSb 结构出现的自旋极化,可通过Rashba 型SOC 效应进行有效地控制,即通过外加电场调控.之所以可调控,源于电子在SLSN 结构中的有效势(Ueff)对Rashba 型SOC 效应强度(η)的依赖性(方程(4)).而且,Rashba 型SOC 效应对基于SLSN-InSb 结构的电子自旋过滤器的调控与电子能量有关,比如在能量E=0.2 eV 附近调控作用相对强些.
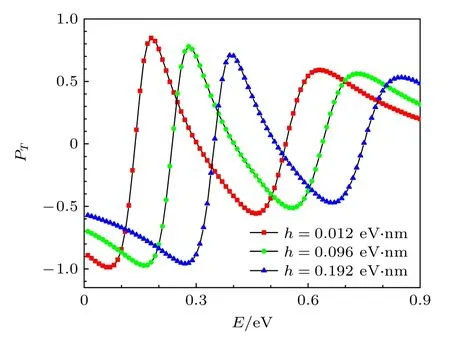
图4 Rashba 型SOC 强度不 同时,外加 电场对 电子自 旋极化的影响,图中其他参数为k//=0.2 nm–1,V=0.32 eV,d=8.0 nmFig.4.Effects of externally applied electric field on the electron-spin polarization for the different Rashba-SOC strengths,where other parameters are k//=0.2 nm–1,V=0.32 eV,d=8.0 nm.
最后,探讨通过改变半导体InSb 层的厚度实现对基于SLSN-InSb 结构的电子自旋过滤器的调控.这是一个值得细心研究的问题,因为由方程(4)可知,电子在SLSN-InSb 结构中经历的有效势(Ueff)与InSb 半导体层的宽度(d)密切相关,因此电子的自旋极化效应将随着半导体层厚度的变化做相应地改变,这允许我们去有效地操控基于SLSNInSb 结构的电子自旋过滤器的性能(自旋极化率).为了找到其规律,图5 给出了半导体层厚度分别为d=8(方形),10(圆形),12 nm(三角形)时,自旋极化率(PT)随着电子能量(E)变化的情况,图5其他结构参数取V=0.32 eV 和η=0.012 eV·nm.如果半导体InSb 层的厚度变宽,自旋极化率增大,同时它的谱线向着高能方向扩展.因此,我们的确可以通过适当地调整半导体InSb层的厚度,很好地控制基于SLSN 结构的电子自旋过滤器件.同时也应注意到,半导体层宽对该自旋过滤器调控的程度与电子的能量有关: 一般在能量较大时控制效果好些,这是因为电子在SLSN-InSb 结构中所感受到的有效势依赖于其能量.
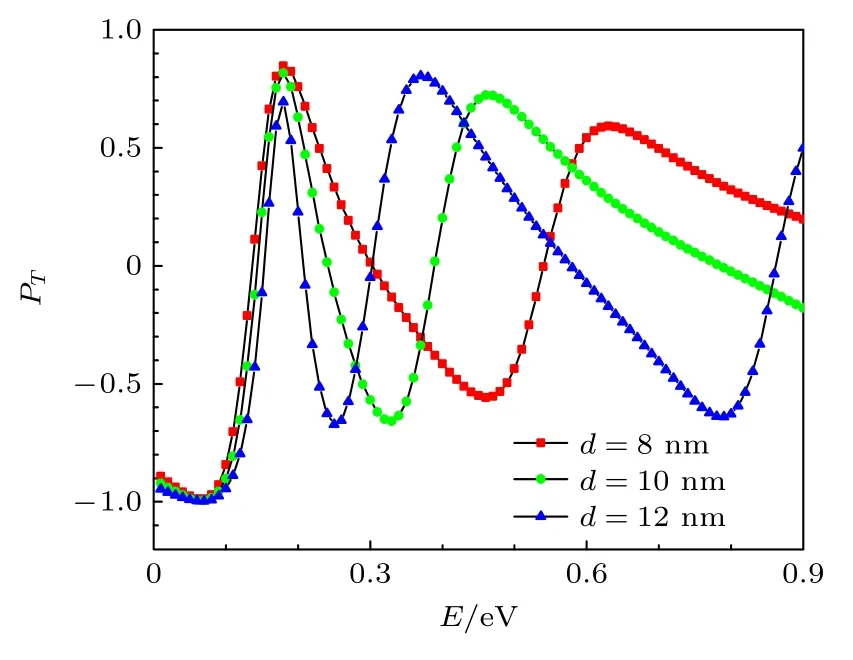
图5 InSb 层厚度不同时,外加电场对电子自旋极化的影响,图中其他参数为k//=0.2 nm–1,V=0.32 eV,η=0.012 eV·nmFig.5.Effects of externally applied electric field on the electron-spin polarization for the different InSb-layer thickness,where other parameters are k//=0.2 nm–1,V=0.32 eV,η=0.012 eV·nm.
4 结论
从理论上研究了电子在一个真实的SLSN-InSb结构中的自旋极化效应,其由外加电场所导致的Rashba 型SOC 产生.在这个SLSN 结构中,发现了Rashba 型SOC 诱发的电子自旋极化效应,其使得该SLSN 结构可以作为一个电子自旋过滤器件.自旋极化率不仅与电子能量和在平面内的波矢有关,而且可以通过外加电场或InSb 层厚度进行调控,因此,该SLSN-InSb 结构可作为自旋电子学器件应用中的可控电子自旋过滤器.
