AlN/β-Ga2O3 异质结电子输运机制*

周展辉 李群 贺小敏

(西安理工大学自动化与信息工程学院,西安 710048)

β-Ga2O3 具有禁带宽度大、击穿电场强的优点,在射频及功率器件领域具有广阔的应用前景.β-Ga2O3 (¯201)晶面和AlN (0002)晶面较小的晶格失配和较大的导带阶表明二者具有结合为异质结并形成二维电子气(twodimensional electron gas,2DEG)的理论基础,引起了众多研究者关注.本文利用AlN 的表面态假设,通过求解薛定谔-泊松方程组计算了AlN/β-Ga2O3 异质结导带形状和2DEG 面密度,并将结果应用于玻尔兹曼输运理论,计算了离化杂质散射、界面粗糙散射、声学形变势散射、极性光学声子散射等主要散射机制限制的迁移率,评估了不同散射机制的相对重要性.结果表明,2DEG 面密度随AlN 厚度的增加而增加,当AlN 厚度为6 nm,2DEG 面密度可达1.0×1013 cm–2,室温迁移率为368.6 cm2/(V·s).在T <184 K 的中低温区域,界面粗糙散射是限制2DEG 迁移率的主导散射机制,T >184 K 的温度区间,极性光学声子散射是限制2DEG 迁移率的主导散射机制.

1 引言

早在20 世纪50 年代,科学家们已经就Ga2O3材料开展相关研究,在目前已知的Ga2O3五种同素异形体中,单斜晶系的β-Ga2O3是一种超宽禁带的透明氧化物半导体,化学性质最为稳定,在最近10 年得到了快速发展[1−3].β-Ga2O3具有比传统宽禁带半导体如SiC 和GaN 更大的禁带宽度(4.9 eV)和更高的击穿电场(8 MV/cm)[4−5],电子饱和速度高达 2×107cm·s–1[6],这些突出的材料特性使β-Ga2O3在大功率、高频电子器件和深紫外光电器件领域具有很大的应用潜力.另外,β-Ga2O3可以用熔体生长法制备大尺寸单晶,也可以用分子束外延、脉冲激光沉积、金属有机化学气相沉积等多种方法制备高质量外延薄膜[2,7−8],为β-Ga2O3的大规模应用提供了条件.

β-(AlxGa1–x)2O3合金的禁带宽度在4.9—8.8 eV范围内可调,可以通过外延生长将β-(AlxGa1–x)2O3和β-Ga2O3集成为β-(AlxGa1–x)2O3/Ga2O3(β-AGO/GO)异质结,在界面处形成二维电子气(twodimensional electron gas,2DEG),能够应用于高电子迁移率晶体管(high electron mobility transistor,HEMT)器件[9−11].β-AGO/GO 异质结2DEG 浓度可以通过改变Al 含量或掺杂浓度来实现,但一方面较高的Al 含量(>0.3)会导致β-(AlxGa1–x)2O3出现相分离[12],而高浓度掺杂会带来强烈的杂质散射,限制电子迁移率.对β-AGO/GO 进行调制掺杂是一种能够兼顾电子浓度和迁移率的折中方案,最近报道的调制掺杂的β-AGO/GO 异质结,2DEG 面密度通常在2.0×1012— 6.1×1012cm–2之间,电子迁移率在140—180 cm2/(V·s)之间[9,12−13].但相对于传统的GaN 基异质结,β-AGO/GO 较小的导带阶(0.4 eV,Al 含量为0.3)难以形成1013cm–2量级的2DEG 面密度,并且调制掺杂也增加了工艺复杂度,容易在器件中引入寄生沟道[9].

β-Ga2O3()晶面与纤锌矿结构AlN (0002)晶面具有相似的原子排列,能够形成AlN/β-Ga2O3异质结,是β-Ga2O3HEMT 器件的候选材料.如图1 所示,β-Ga2O3()晶面的Ga 原子和O 原子,AlN (0002)晶面的Al 原子和N 原子,都呈六角形排列,边长分别为1.753 Å和1.797 Å,β-Ga2O3在b轴方向与AlN (0002)晶面的晶格失配为2.4%[14],二者具有结合为AlN/β-Ga2O3异质结的结构基础.近两年,多个研究组都在β-Ga2O3的()晶面上生长出了高质量的AlN/β-Ga2O3和GaN/β-Ga2O3异质结,并利用高分辨透射电子显微镜观察到原子规则排列的界面[15−16],外延关系为β-Ga2O3()//AlN (0002),β-Ga2O3[102]//AlN[-1100][14].AlN/β-Ga2O3HEMT 的仿真研究表明,AlN/β-Ga2O3界面处能够形成面密度为1013cm–2量级的2DEG,并具有优异的功率和频率特性[17,18].相对于β-AGO/GO 异质结,AlN/β-Ga2O3异质结具有形成更高性能2DEG 的潜在优势,包括: 1)AlN 的施主类表面态能够为沟道提供大量电子[19−20];2)AlN 强烈的自发极化、压电极化效应能够诱导电子在AlN/β-Ga2O3界面处聚集[15,21];3)AlN/β-Ga2O3界面更大的导带阶(1.75 eV)能够产生更强的电子限域性[14].但目前,AlN/β-Ga2O3异质结的发展仍处于初级阶段,无论从实验上还是理论上,都需要进一步的研究.

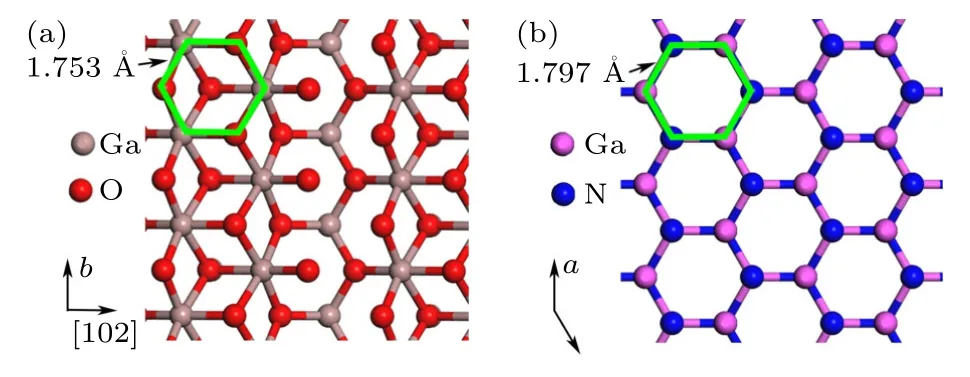
图1 (a) β-Ga2O3 (¯201)晶面和(b)AlN (0002)晶面的原子排列Fig.1.The atomic arrangement in (a) (¯201) plane of β-Ga2O3 and (b) (0002) plane of AlN.

本文基于AlN、β-Ga2O3已知材料特性,对AlN/β-Ga2O3异质结电学特性进行了理论研究,预测了AlN/β-Ga2O3异质结的性能潜力.本文建立了AlN/β-Ga2O3异质结的静电模型,计算了导带形状和2DEG 面密度,分析了AlN 层的临界厚度,并利用玻尔兹曼输运理论,研究了主要散射机制对AlN/β-Ga2O3异质结迁移率的限制作用,计算了AlN/β-Ga2O3异质结电子迁移率随温度的变化关系.本文工作能为AlN/β-Ga2O3异质结工艺优化与器件结构设计提供理论参考.

2 理论模型

2.1 静电模型

传统的III 族氮化物异质结,如AlGaN/GaN,AlN/GaN,InAlN/GaN,能够在不进行故意掺杂的情况下形成面密度高达1013cm–2的2DEG,普遍认为势垒层存在高面密度的施主类表面态,表面态离化后释放出电子在界面处聚集形成2DEG,并在异质结表面留下带正电的离化电荷[19,22−24].AlN/β-Ga2O3异质结采用AlN 为势垒层,也有可能通过表面态产生高面密度的2DEG.因此,本文建立了如图2 所示的表面态模型,认为AlN/β-Ga2O3异质结2DEG 来源于表面态,表面态分布于距离表面导带Ed=2.2 eV 以下的禁带中,浓度为Nsd=5.0×1013cm–2/eV.表面态参数设置参考自III 族氮化物异质结的报道[19].

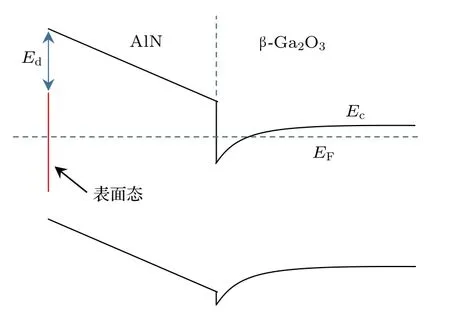
图2 AlN/β-Ga2O3 异质结表面态能级分布示意图Fig.2.Schematic drawing of energy distribution of surface states in an AlN/β-Ga2O3 heterostructure.

定义AlN 的生长方向([0001]晶向)为z轴,AlN/β-Ga2O3界面位置为坐标原点,AlN 和β-Ga2O3层分别位于z <0 和z >0 区域.在有效质量近似下,电子能级Ei和波函数ξi(z)遵循薛定谔方程[25]:

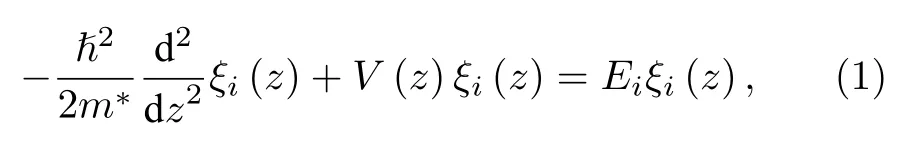
其中,ℏ 为约化普朗克常数,m∗为电子有效质量,势能V(z)与静电势ϕ(z)的关系为V(z)=−eϕ(z)+Θ(−z)⋅∆Ec,e为电子电荷,Θ(z) 为阶跃函数,对z≥0 ,Θ(z)=1 ;对z<0,Θ(z)=0,AlN/β-Ga2O3界面导带阶 ∆Ec=1.75 eV[14].静电势ϕ(z) 由异质结中所有电荷成分共同决定,可以通过泊松方程求得[25]:

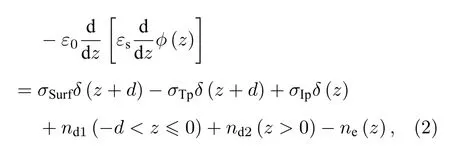
其中,ε0为真空介电常数,εs为相对介电常数,d为AlN 层厚度,σSurf为离化表面态电荷面密度,σTp和σIp分别为AlN 上、下表面的极化电荷面密度,ne(z) 为电子浓度,nd1和nd2分别为AlN 和β-Ga2O3离化施主电荷浓度.在这些电荷成分中,σSurf和σTp为σIp为z向的δ函数,其余电荷成分为体函数.

假设在β-Ga2O3()晶面上外延的AlN 处于完全应变状态,AlN 在[0001]方向的自发极化强度PSP=−0.081 C/m2,压电极化强度为[26]?

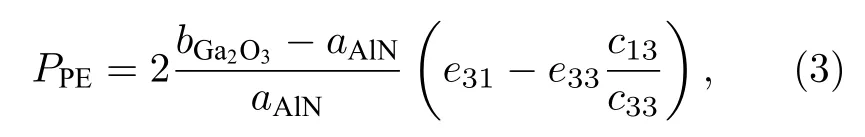
其中 aAlN为弛豫状态的AlN 晶格常数,e31,e33分别为AlN 压电常数,c13,c33为AlN 弹性系数,为β-Ga2O3晶格常数.AlN 上、下表面极化电荷面密度分别为

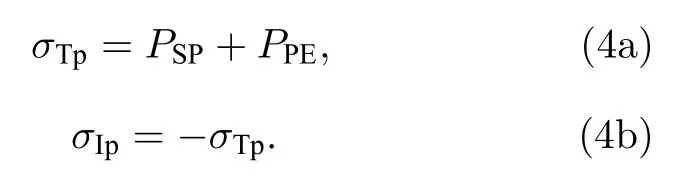
值得注意的是,与AlN/GaN 异质结不同,AlN/β-Ga2O3异质结中,AlN 为压应变,压电极化强度指向[0001]方向,与自发极化强度相反,压电极化强度抵消了部分自发强化强度,但AlN 下表面仍带有净剩的正极化电荷.

为了数学上的简化,近似认为能量大于费米能级EF的表面态全部离化,则离化的表面态面密度σSurf表示为[18,27]

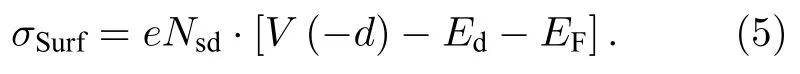
电子分布ne(z) 表示为[28]

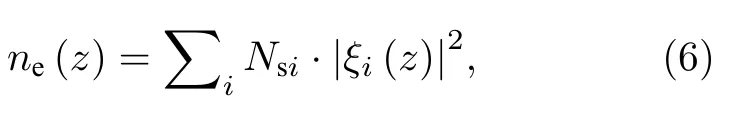
其中Nsi为子带能级Ei上的电子面密度,取决于EF与Ei的相对位置,将费米-狄拉克公式在整个能量范围内进行统计得到[29]:

异质结中所有电荷成分应满足电中性条件:

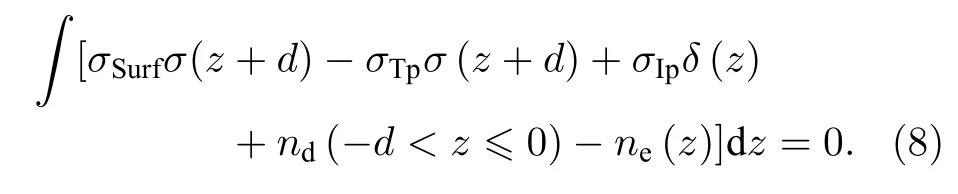
求解 (1)—(8)式可以分析AlN/β-Ga2O3异质结导带能量和2DEG 面密度等电学性质.

2.2 迁移率模型

本文考虑声学形变势(deformation potential,DP)散射、离化杂质散射(ionized impurity scattering,IIS)、界面粗糙散射(interfacial roughness scattering,IRS)、极性光学(polar optical,PO)声子散射等散射机制对2DEG 迁移率的限制作用.DP,IIS,IRS 为弹性散射机制,可以利用解析表达式来计算能量为E的电子动量弛豫时间τi(E),其中i=DP,IIS,IRS,对动量弛豫时间进行能量平均[30]:

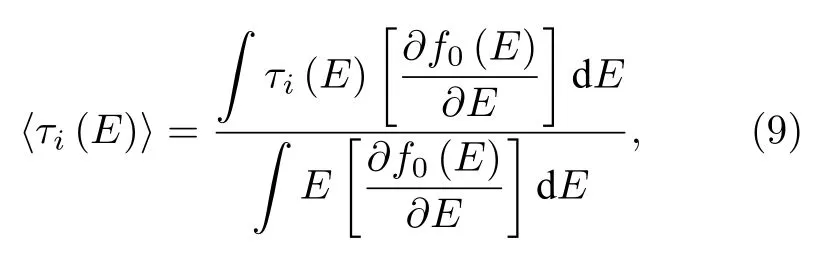
其中,f0(E) 为费米-狄拉克分布函数:

各散射机制限制的迁移率为µi=e〈τi(E)〉/m∗.使用马西森定则得到总的迁移率[30]:

2.2.1 声学形变势散射

声学DP 散射是在中低温度区域限制电子迁移率的主要散射机制之一.2DEG 输运过程中,费米能级附近的电子是迁移率的决定因素,而声学声子能量通常远小于费米能级,因此声学声子散射过程可以近似为弹性碰撞.声学DP 散射矩阵元由下式给出[31]:

其中D为声学形变势,V为体积,ρ为质量密度,ul为声速,动量弛豫时间的倒数为[31]

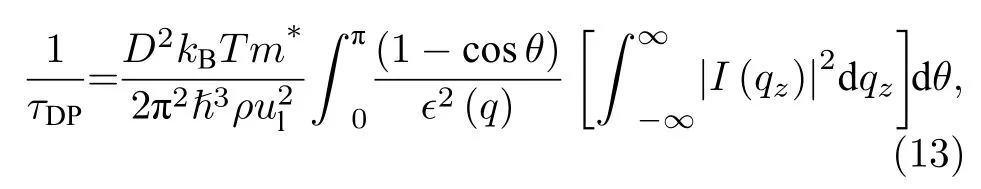
其中θ为散射角,q和qz分别为平行、垂直于AlN/β-Ga2O3界面方向的声子波矢分量.本文只考虑第一子带内的电子散射,散射重叠因子I(qz)=采用绝对零度的随机相近似,屏蔽因子ϵ(q) 表示为[32]

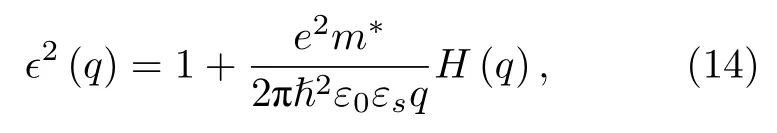
其中,形状因子H(q) 可写为[32]

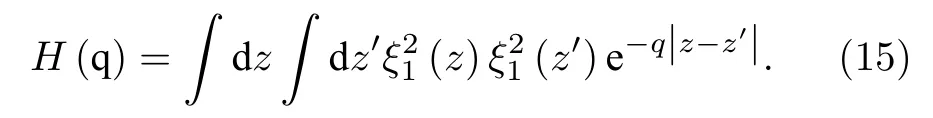
该屏蔽因子同样应用于其他散射机制.

2.2.2 界面粗糙散射

本文使用高斯形式的相关函数C(r)=通过平均粗糙高度∆和水平相关长度Λ两个参数描述界面粗糙度,散射矩阵元表述为[34]:

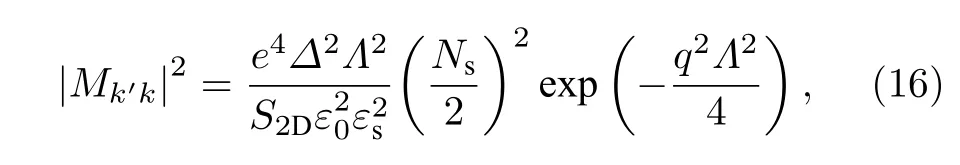
其中S2D为样品面积,动量弛豫时间的倒数为[30]:

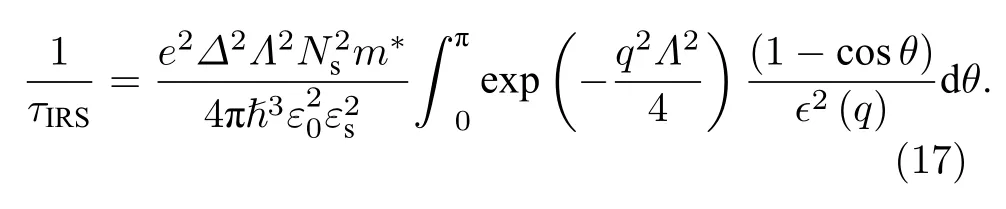
2.2.3 离化杂质散射

AlN/β-Ga2O3异质结中存在故意或非故意掺杂,杂质会引起晶格畸变,通过形变势散射电子,电离杂质还可以通过库仑作用散射电子.通常来说,晶格畸变造成的散射远小于库仑散射[35],所以本文只考虑电离杂质的库仑散射,离化杂质的散射矩阵元可以表述为[36]

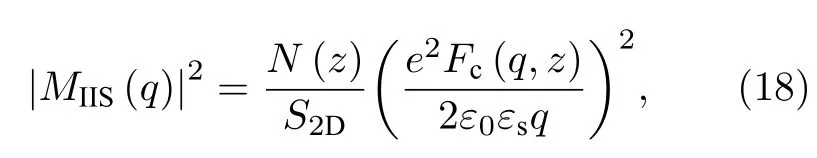
其中N(z) 指的是电离杂质浓度,Fc(q,z) 为[30]

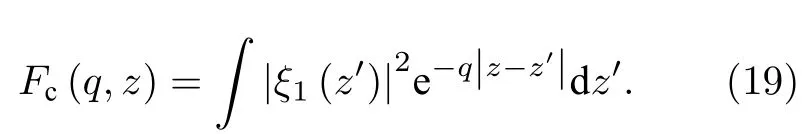
动量弛豫时间的倒数为[30]

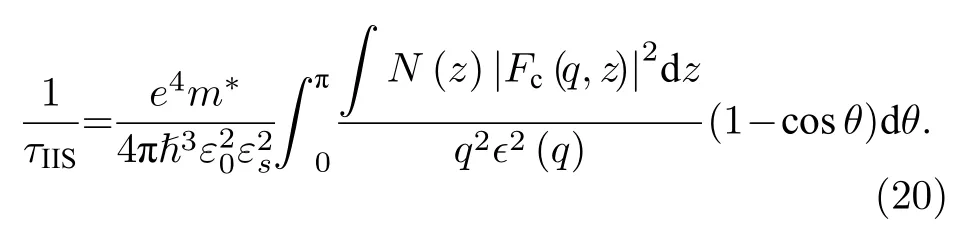
本文假设AlN 和β-Ga2O3层各有均匀分布的背景电离杂质,浓度分别为N(z)=nd1=1×1017cm−3和N(z)=nd2=1×1016cm−3.

2.2.4 极性光学声子散射

PO 声子的能量与费米能级相当,对电子产生非弹性散射,不能准确定义解析形式的动量弛豫时间,需要直接求解玻尔兹曼输运方程来获得精确的PO 声子散射率.

PO 声子散射矩阵元为[37]

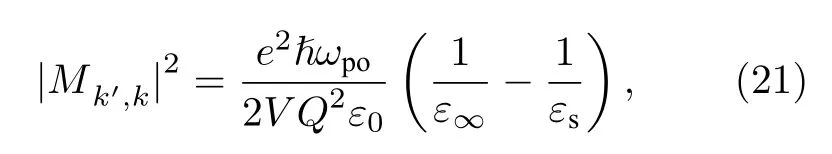
其中,ℏωpo为PO 声子能量,ε∞为高频介电常数,Q为三维声子波矢.将玻尔兹曼输运方程应用于极性光学声子散射,可以得到

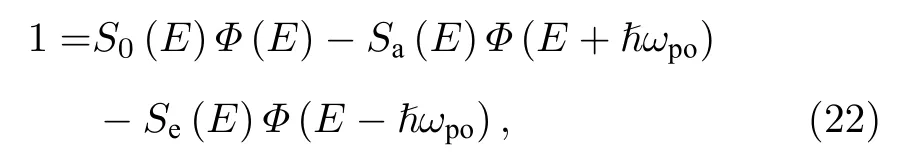
其中,Φ(E)是需要确定的微扰项,S0(E) 表示k态电子经PO 声子散射跃迁到k′态的散射率,Sa(E)和Se(E) 分别为k′态电子吸收、释放1 个PO 声子跃迁到k态的散射率,具体的表达式可以参考Kawamura 等[32]的报道.本文使用迭代法求解(22)式,将求得的Φ(E) 代替(9)式中的τi(E) 可以获得PO 声子散射的动量弛豫时间〈τPO(E)〉.如果在(22)式中使用代替S0(E),其中为本文考虑的弹性散射率之和,则可以得到所有散射机制共同限制的动量弛豫时间〈τTOT(E)〉.

3 结果与分析

论文使用Octove 软件编程,依次计算了表面态模型和迁移率模型,材料参数如表1 所示.

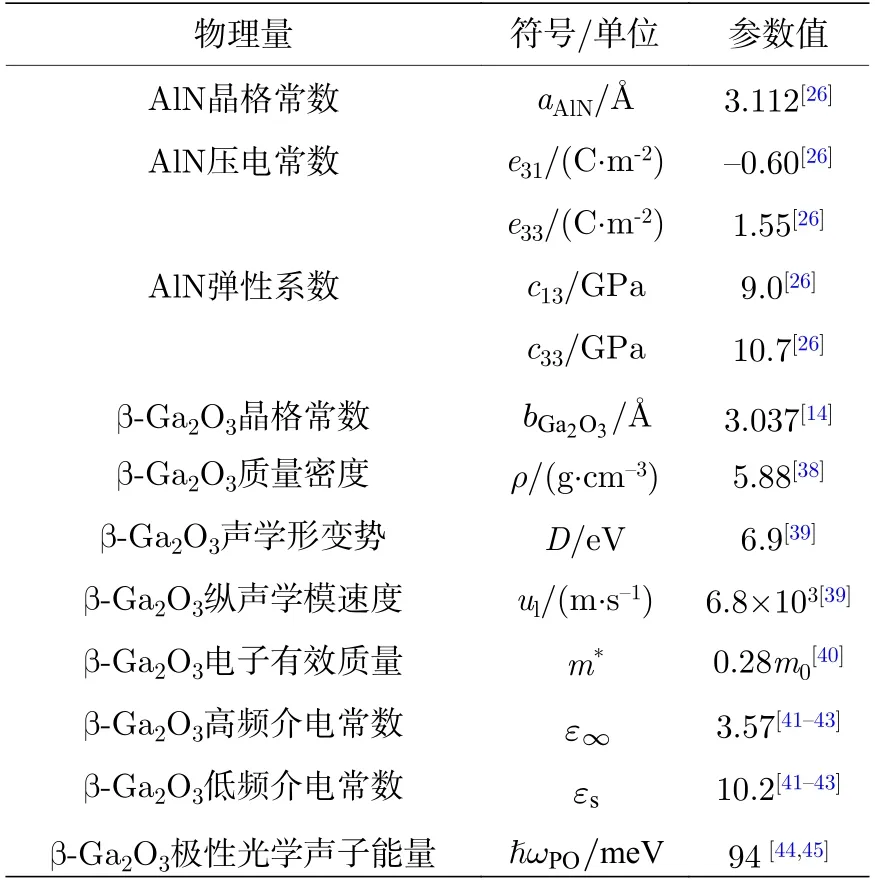
表1 计算过程中用到的AlN/β-Ga2O3 异质结参数(m0 为自由电子质量)Table 1.Parameters of AlN/β-Ga2O3 heterostructure employed in calculations (m0 is the free electron mass).

图3 为利用均匀分布表面态模型计算得到的AlN/β-Ga2O3异质结导带形状和电子浓度分布,AlN 厚度d=6 nm.AlN 势垒层位于z<0 区域,AlN 自发极化效应与压电极化效应,在AlN 层形成垂直于AlN/β-Ga2O3界面的极化场,导致AlN层导带形状近似线性变化.AlN 层极化效应在AlN/β-Ga2O3界面引起面密度为2×1013cm–2的正极化电荷,结合AlN/β-Ga2O3界面1.75 eV 的导带阶,使得电子密集聚集在界面处β-Ga2O3一侧,形成高浓度2DEG.β-Ga2O3深处电场为0,导带能量随着远离界面渐变为常数.2DEG 面密度NS=1.0×1013cm−2,最高电子浓度为4.3×1019cm–3.沟道中 92%的电子分布在界面附近5 nm 范围内,电子到界面的平均距离为2.2 nm.由于背景杂质浓度较小,对导带形状与2DEG 浓度的影响不大.

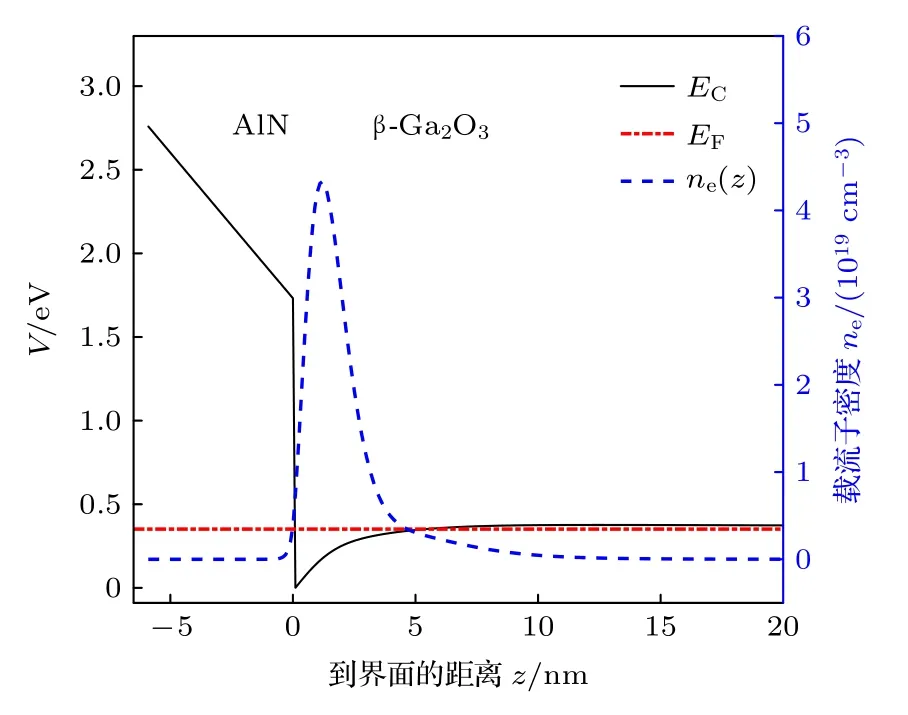
图3 AlN/β-Ga2O3 异质结导带形状和2DEG 浓度分 布,AlN 厚度 d=6 nmFig.3.The conduction band profile and spatially distributed density of the 2DEG in an AlN/β-Ga2O3 heterostructure with an AlN thickness of 6 nm.

图4 为AlN/β-Ga2O3异质结2DEG浓度对AlN 厚度的依赖关系.结合图2 可知,随着AlN 层厚度的增大,越来越多的表面态上升到费米能级以上,释放出更多电子,形成了面密度更大的2DEG.但随着AlN 厚度增大,费米能级随之增大,导带底到费米能级的能量差即表面势增长速度降低,导致2DEG 面密度增长趋势变缓.

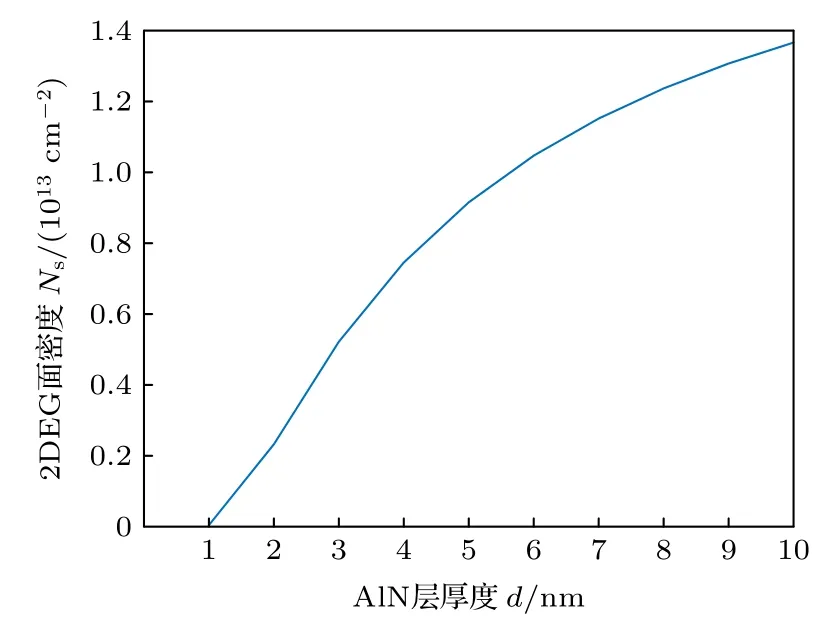
图4 2DEG 面密度对AlN 厚度的依赖关系Fig.4.Dependence of the 2DEG sheet density on the AlN thickness.

需要注意的是,AlN 和β-Ga2O3存在2.4%的晶格失配[14],随着AlN 厚度增大到临界厚度以上,AlN 层将因应力过大发生晶面滑移,产生应力弛豫现象,影响器件性能和可靠性.因此,器件设计应使AlN 层保持在临界厚度以下.Fischer 等[46]指出,异质外延的半导体薄膜,外延层应变与失配位错满足下面的关系:

代入β-Ga2O3晶格常数=0.3037 nm[14],AlN 晶格常数aAlN=0.3112 nm,AlN 泊松比v=0.608[47],考虑到失配位错更有可能是刃位错,取位错伯格斯矢量绝对值b=0.3037 nm,λ为位错伯格斯矢量与界面方向的夹角,α是伯格斯矢量与位错线方向的夹角,λ和α分别取0°和90°.最终计算得到AlN 层的临界厚度hc=7.09 nm.在后续计算中,除非特殊说明,选取AlN 层厚度为6 nm.

图5 为IRS 限制的迁移率对水平相关长度Λ的依赖关系.界面粗糙限制的迁移率随Λ的增大先减小后增大,呈“V”字形变化.Λ<1.5 nm 时,越小的Λ意味着界面高度在沿界面方向的变化越迅速,固定长度范围内的高度平均值越均匀,相应的迁移率越大.IRS 限制的迁移率在Λ=1.5 nm 时取得最小值.当Λ进一步增大,意味着界面高度的变化越来越平缓,IRS 限制迁移率也越来越大.对于给定的Λ,IRS 限制的迁移率与平均粗糙高度的平方∆2呈反比关系.

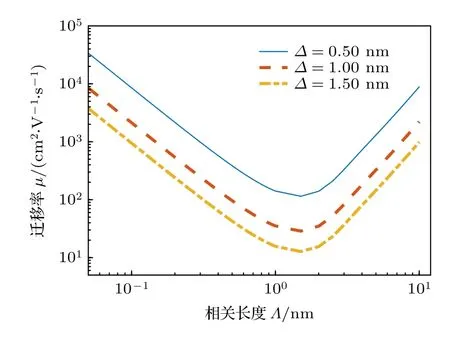
图5 IRS 限制的迁移率对相关长度 Λ 的依赖关系Fig.5.Dependence of the mobility limited by IRS on correlation length Λ for different roughness heights.

图6 为300 K 时各弹性散射机制限制的动量弛豫时间对电子能量的依赖关系.随着能量的增大,τIIS与τIRS单调增大,τDP单调减小.在界面粗糙散射和离化杂质散射中,电子能量越大,散射角越小,电子波矢改变量越小,动量弛豫时间越大.但声学形变势散射是近程散射机制,电子能量增大不会显著影响散射角,且高能电子受到的屏蔽效应更弱,导致τDP随能量的增大而减小.

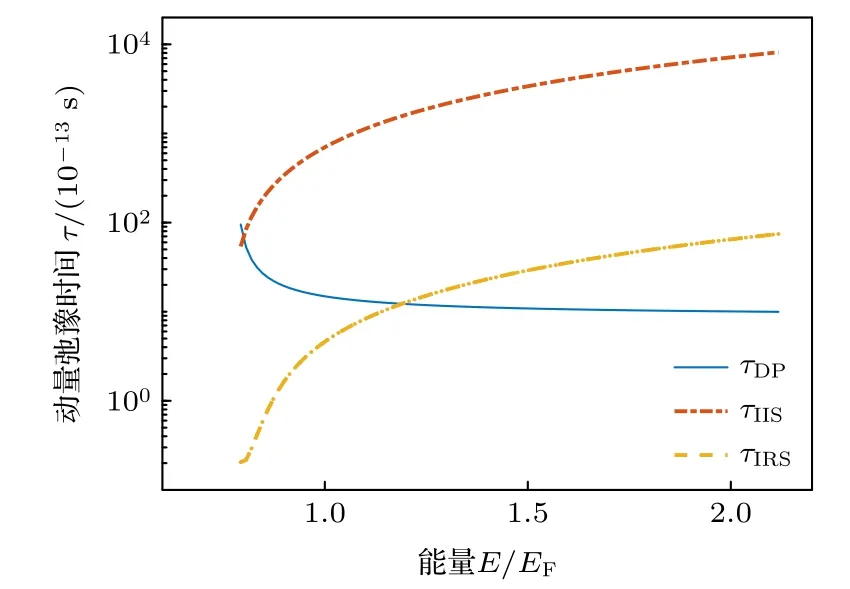
图6 300 K 时离化杂质散射限制的动量弛豫时间(τIIS)、界面粗糙散射限制的动量弛豫时间(τDP)、声学形变势散射限制的动量弛豫时间(τDP)对电子能量的依赖关系Fig.6.Dependence of the momentum relaxation time limited by ionized impurity scattering (τIIS),interface roughness scattering (τIRS) and acoustic DP scattering (τDP) on the electron energy.

图7 显示了弹性散射限制的动量弛豫时间τELA及所有散射机制限制的动量弛豫时间τTOT对能量的依赖关系.随着电子能量的增大,τELA单调增长,但考虑PO 声子散射影响的τTOT随着电子能量的增大而间断地发生跃变.这是因为每当电子能量(Ek=E −E1,E1表示第一子带的能量)增加PO 声子能量 ℏωpo的整数倍时,电子就会具备发射更多PO 声子的能力,因此τTOT突然减小.在低温区域,PO 声子数目很少,且低能电子(Ek/ℏωpo<1)不满足发射PO 声子的条件,所以PO 散射对低温区域低能电子的影响很小,τTOT与τELA几乎重合.当电子能量增大到足以发射PO 声子(Ek/ℏωpo>1),PO 散射作用不可忽略,所以τTOT与τELA存在巨大差异.在高温区域,PO 声子的数目很多,低能电子也可以通过吸收PO 声子而被散射,因此τTOT在整个能量范围内都小于τELA.

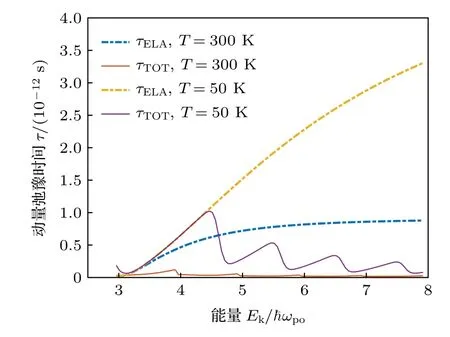
图7 动量弛豫时间对电子能量的依赖关系Fig.7.Dependence of the momentum relaxation time on the electron energy.

图8 为各散射机制限制的迁移率对2DEG 面密度的依赖关系.IIS 通过库仑作用散射电子,随着2DEG 浓度的增长,屏蔽作用增强,所以IIS 限制的迁移率增加.高浓度的2DEG 会产生更强局域场将电子进一步推向界面,电子受到更强烈的IRS,使得IRS限制的迁移率单调下降.2DEG面密度上升导致费米能级上升,而费米能级附近的电子是决定迁移率的主要因素,DP 散射和PO 散射对能量的依赖导致迁移率随2DEG 面密度增大而减小.

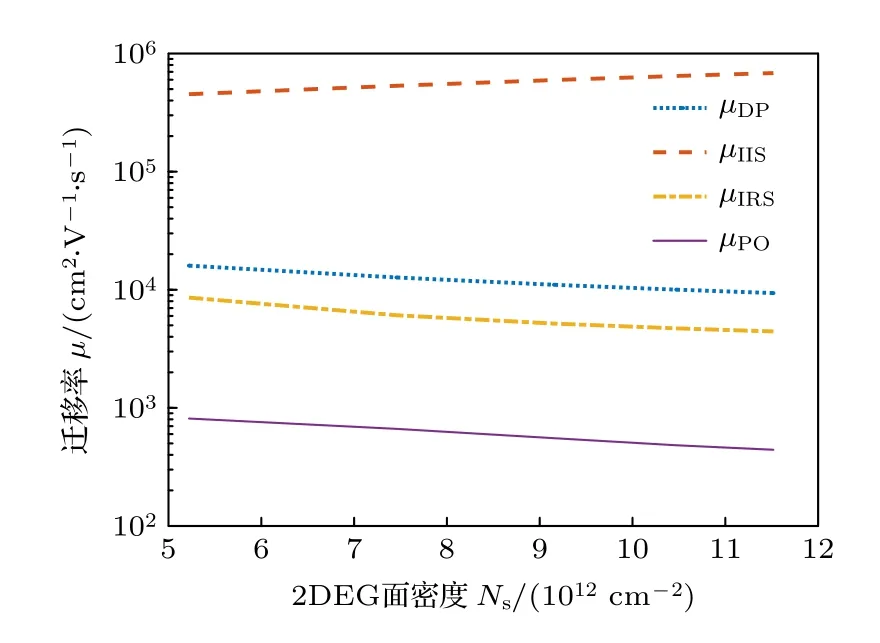
图8 300 K 时离化杂质散射限制的迁移率(µIIS)、界面粗糙散射限制的迁移率(µIRS)、声学形变势散射限制的迁移率(µDP)、极性光学声子散射限制的迁移率(µPO)对2DEG 面密度的依赖Fig.8.Dependence of the mobility limited by ionized impurity scattering (µIIS),interface roughness scattering(µIRS),acoustic DP scattering (µDP) and PO phonon scattering (µPO) on the 2DEG sheet density at 300 K.

图9 为各散射机制分别限制的迁移率以及共同作用下的总迁移率随温度的变化关系.IRS 与IIS 限制的迁移率对温度的微弱依赖,来自于温度对屏蔽效应、费米能级等因素的影响.由于本文只考虑了浓度很小的背景离化杂质,IIS 对迁移率的限制作用远小于IRS.温度较低时,声学声子和极性光学声子数目很少,对迁移率的影响很小,因此T <148K 的中低温区域,IRS 是限制迁移率的主导机制.温度升高导致声学声子数目和极性光学声子数目快速增加,因此声学DP 和PO 声子散射限制的迁移率随温度的升高而减小.且由于极性光学声子能量更大,对电子的散射造成更大的能量、动量损失,因此PO 声子限制的迁移率下降速度更快.T >148 K 的中高温区域,PO 声子散射是限制迁移率的主导散射机制.300 K 时,各种散射机制限制共同作用限制的迁移率为368.6 cm2/(V·s),大于已有报道的β-AGO/GaO 异质结电子迁移率[9,12−13].并且,值得注意的是,根据各散射机制对2DEG 面密度依赖关系(见图8),通过减小AlN厚度来降低2DEG 面密度降,可以进一步使AlN/β-Ga2O3异质结室温迁移率上升到500 cm2/(V·s)以上.

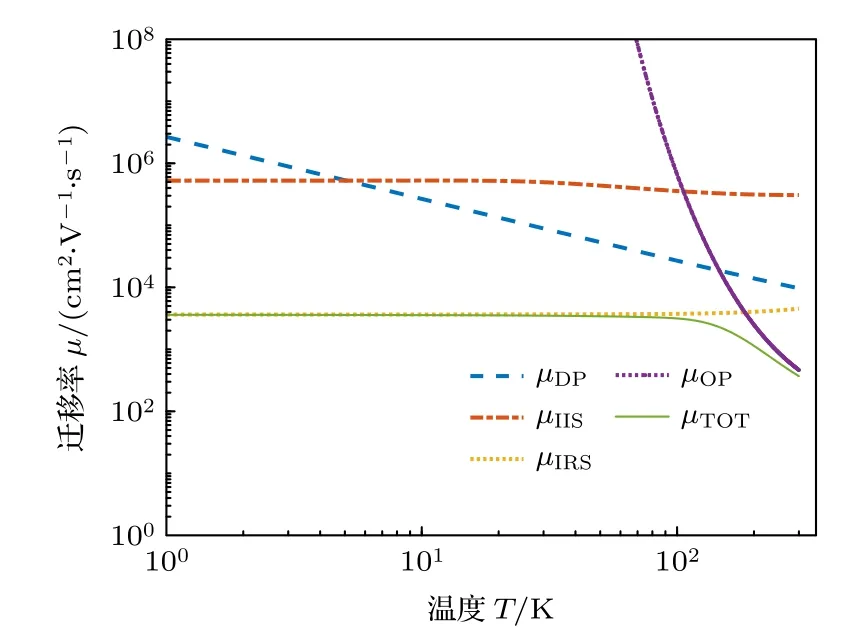
图9 µDP,µIIS,µIRS,µPO 以及总的迁移率(µTOT)对温度的依赖关系,相关长度 Λ=5 nm,粗糙高度∆=1 nmFig.9.Temperature dependence of the µDP,µIIS,µIRS,µPO,and the total mobility µTOT,the correlation length Λ=5nm and roughness height ∆=1 nm.

4 结论

本文基于表面态模型计算了AlN/β-Ga2O3异质结2DEG 面密度,并利用玻尔兹曼输运理论研究了电子输运特性.结果显示,AlN/β-Ga2O3异质结2DEG 面密度随AlN 厚度的增大而增大,AlN厚度为6 nm 时的2DEG 面密度为1.0×1013cm–2.在非故意掺杂的情况下,界面粗糙散射是中低温区域限制电子迁移率的主导机制,极性光学声子散射是高温区域限制迁移率的主导机制,300 K 时电子迁移率为368.6 cm2/(V·s).