利用含δ 介子的相对论平均场理论研究中子星潮汐形变性质

刁彬 许妍† 黄修林 王夷博

1) (中国科学院国家天文台长春人造卫星观测站,长春 130117)

2) (中国科学院大学天文与空间科学学院,北京 100049)

开展中子星宏观性质的研究,对于揭示中子星内部组成和结构具有重要意义.本文基于相对论平均场理论模型,研究了 δ 介子对传统中子星和超子星物态方程、最大质量、勒夫数和潮汐形变能力的影响.结果表明,对于中小质量传统中子星(或超子星),δ 介子使其潮汐形变能力变强;随着传统中子星(或超子星)质量的增加,δ 介子对其潮汐形变能力影响逐渐减弱;尤其对于大质量超子星,含有δ 介子的超子星潮汐形变能力相比不含δ 介子的超子星变弱.此外,在相同质量下超子的存在会降低星体的潮汐形变能力,在本文所选的参数下,含有δ介子的星体中,仅同时含Λ,Σ和Ξ超子的超子星潮汐形变能力能同时满足GW170817 和GW190814 天文观测约束.随着与中子星相关的引力波数据逐渐增加,将为人们判断超子星内超子种类提供一个可能的途径.

1 引言

中子星是宇宙中除黑洞以外最致密的一类星体,对于中子星性质的研究为人们理解极端条件下高密物质的性质和行为提供了新的维度.1967 年,Hewish 等[1]发现第一颗脉冲星PSR B1919+21,不久Gold[2]就证实其为一颗快速旋转的中子星,随后关于中子星物态方程的研究迅速发展.然而,由于中子星内部结构主要由参与强相互作用的粒子主导,当前研究人员只能借助地面核实验和天文观测如中子星质量、半径、引力波辐射等对中子星宏观性质进行限制,通过唯象或微观核多体理论模型对中子星物态方程和内部结构展开了大量的研究[3−12].

2017 年8 月17 日,激光干涉引力波天文台和室女座引力波天文台等成功探测到双中子星并合引力波信号即GW170817 事件,则为研究中子星物态方程打开了新的窗口[13].在双星系统中,一般用无量纲的潮汐形变因子Λtidal来反映星体的潮汐形变能力,而潮汐形变因子又与星体的物态方程息息相关.双星系统的演化一般分为旋进、并合、铃宕三个阶段.双中子星相互绕转时,会因辐射引力波而相互靠近.在旋进的后期,因为伴星的存在使得中子星发生潮汐形变,星体的潮汐形变因子可由这一阶段的引力波信号与点质量结果的偏离给出.因此,可以用双中子星并合的引力波信号来限制中子星物态方程.到目前为止,已发现了5 例与中子星相关的引力波事件即: GW170817,GW190814,GW190425,GW200105 和GW200115[14−17].基于GW170817 和GW190814 事件,学者指出 1.4M⊙中子星潮汐形变因子取值范围分别为和这些引力波事件对限制中子星物态方程、分析星体内部物质成分产生了深远影响[18−22].

许多学者针对中子星潮汐形变性质开展了大量意义深刻的工作.2018 年,Zhu 等[23]提出了一种可以很好地描述GW170817 观测结果并能约束夸克层次中子星物态方程,即“QMF18”模型.2019年,Biswas 等[24]利用GW170817 事件对中子星内部压强的各向异性进行了研究,指出压强的各向异性能大幅降低中子星潮汐形变能力.2020 年,Essick 等[25]利用非参数方法分析了中子星物态方程、内部物质成分和星体最大质量,并指出GW170817事件支持软的中子星物态方程并强调了利用引力波数据约束中子星物态方程的良好前景.2021 年,Miao 等[26]用贝叶斯统计方法基于GW170817,GW190425 和PSR J0030+0451 的天文观测约束研究了中子星转动惯量,在90%可信度下估算了PSR J0737—3039 的转动惯量理论值范围.2022年,Huang 等[27]利用相对论平均场理论模型研究了超子星潮汐形变性质,指出引力波探测为研究中子星结构提供了良好的途径,希望未来可以从引力波中得到特殊的信号,帮助人们确定中子星内是否包含超子.如果中子星内部出现超子,如何判断超子的种类一直都是中子星物态方程研究中的热点和焦点问题,并且为了能够体现星体内核子(n和p)或超子(Λ,Σ 和Ξ)有效质量的差别,学者们在相对论平均场理论模型中引入了同位旋矢量-标量介子δ 来描述星体的性质.1997 年,Kubis 和Kutschera[28]在相对论平均场理论模型下研究了δ 介子对中子星性质的影响,指出δ 介子使得中子单粒子能增加,质子丰度增加,并且中子和质子的有效质量会发生劈裂.2009 年,喻孜等[29]在相对论平均场理论模型下研究了δ 介子对热前中子星性质的影响,指出δ 介子使得热前中子星内超子丰度升高,但是这种趋势会随着星体温度的升高逐渐减弱.2010 年,邵国运和刘玉鑫[30]在相对论平均场理论模型下研究了δ 介子对含和不含反K 介子凝聚相超子星粒子分布、半径和质量的影响.2018 年,孙保元等[31]利用相对论平均场理论模型展开了δ 介子对星体转动惯量研究,指出δ 介子会抑制星体壳层和总的转动惯量,并使得壳层转动惯量和星体总转动惯量的比值也受到抑制.前人的工作表明,δ 介子出现会改变星体微观和宏观性质[32−36],这必然也会改变星体潮汐形变性质.因此,本文在相对论平均场理论框架下主要研究δ 介子对传统中子星和超子星潮汐形变性质的影响.

本文将在第2 节给出包含δ 介子的相对论平均场理论模型下传统中子星和超子星物态方程,广义相对论流体静力学平衡方程和求解中子星潮汐形变因子微分方程;第3 节讨论传统中子星和超子星物态方程、质量-半径关系、勒夫数和潮汐形变因子在考虑和不考虑δ 介子时将有怎样的变化;第4 节对本文研究进行总结.

2 理论基础

2.1 包含 δ 介子的相对论平均场理论模型

在本文中,为了更直观地说明δ 介子对星体潮汐形变性质的影响,将采用包含σ,ω,ρ 和δ 介子一种比较简化的相对论平均场方法[37−41].其中同位旋标量-标量介子σ 反映重子间吸引力,同位旋标量-矢量介子ω 反映重子间短程排斥力,同位旋矢量-矢量介子ρ 反映中子和质子的差别,同位旋矢量-标量介子δ 反映属于同一种类但具有不同同位旋量子数重子有效质量的差别.

描述中子星物质的拉格朗日密度可以写成以下三个部分:

把拉格朗日密度(1)式—(4)式代入Euler-Lagrange 方程,在相对论平均场近似下,重子场和介子场运动方程可以简化为

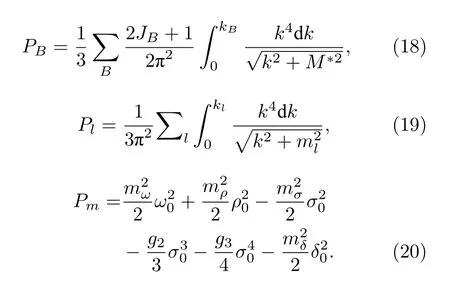
2.2 广义相对论流体静力学平衡方程

为了获得中子星质量 (M) 和半径 (R),我们常常需要借助广义相对论流体静力学平衡方程[43,44],其具体的表达式如下:

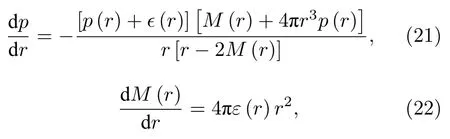
其中p(r),ϵ(r)和M(r) 分别表示半径r处星体的压强、能量密度和质量.结合物态方程(13)—(20),可以获得中子星质量-半径关系,由此可以把理论结果与中子星质量测量数据联系起来.

2.3 中子星潮汐形变因子

yR可以通过求解如下微分方程获得[47]

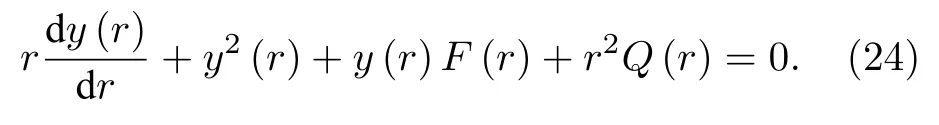
方程(23)满足边界条件y(0)=2[48],p(0)=pc和M(0)=0,式中F(r) 与Q(r) 都是中子星E(r),P(r)和M(r) 的函数,具体表达式如下:

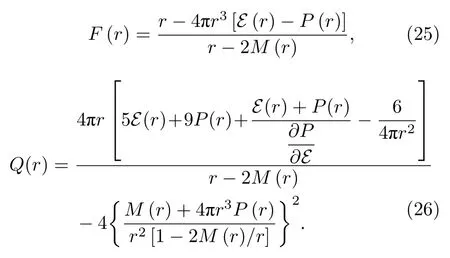
中子星潮汐形变因子可以表示为k2,M和R的关系,具体表达式如下:

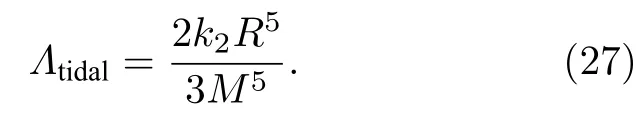
结合中子星物态方程和广义相对论流体静力学平衡方程,可以获得星体的潮汐形变因子理论值.

3 中子星宏观性质及数值结果

在本文中,采用了较简单的中子星模型,假设中子星核心是由n,p和l(传统中子星)或n,p,l,Λ,Σ+,Σ0,Σ−,Ξ−和 Ξ0(超子星)组成.前人的工作表明: 中子星内出现同位旋矢量-标量δ 介子会改变星体物态方程,使得星体内部物质状态发生一系列改变,因此必然会影响星体的潮汐形变性质.因此,在本文中着重分析δ 介子对传统中子星和超子星潮汐形变性质的影响,主要分以下6 种情况讨论: 1) 不考虑δ 介子的影响,中子星核心仅含有核子n,p和轻子l(记作pn,no δ);2) 考虑δ 介子的影响,中子星核心仅含有核子n,p和轻子l(记作pn,with δ);3) 不考虑δ 介子的影响,中子星核心含有重子n,p,Λ,Ξ 和轻子l(记作pnH no Σ,no δ);4) 考虑δ 介子的影响,中子星核心含有重子n,p,Λ,Ξ 和轻子l(记作pnH no Σ,with δ);5) 不考虑δ 介子的影响,中子星核心含有重子n,p,Λ,Σ,Ξ 和轻子l(记作pnH,no δ);6)考虑δ介子的影响,中子星核心含有重子n,p,Λ,Σ,Ξ 和轻子l(记作pnH,with δ),计算过程中涉及的参数和饱和密度处核物质性质分别列在表1和表2 中.

表1 各参数的取值.其中,fi=(gi/mi)2(fm2),i=σ,ω,ρ和δ .介子质量取值如下: mσ=550 MeV,mω=783 MeV,mρ=763 MeV 和 mδ=983 MeV .超子耦合常数表示为与核子耦合常数的比值,即 xi=giH/gi,i=σ,ω,ρ和δ,具体取值为 xωB=0.783,xσB=xδB=xρB=0.7[49]Table 1.Parameter sets.fi=(gi/mi)2fm2,i=σ,ω,ρ and δ,we take mσ=550 MeV ,mω=783 MeV ,mρ=763 MeV and mδ=983 MeV .The ratios of coupling constants between hyperons and nucleons can be expressed xi=giH/gi,i=σ,ω,ρ and δ.Their values x ωB and xσB , xδB , xρB are 0.783 and 0.7,respectively [49].

表1 各参数的取值.其中,fi=(gi/mi)2(fm2),i=σ,ω,ρ和δ .介子质量取值如下: mσ=550 MeV,mω=783 MeV,mρ=763 MeV 和 mδ=983 MeV .超子耦合常数表示为与核子耦合常数的比值,即 xi=giH/gi,i=σ,ω,ρ和δ,具体取值为 xωB=0.783,xσB=xδB=xρB=0.7[49]Table 1.Parameter sets.fi=(gi/mi)2fm2,i=σ,ω,ρ and δ,we take mσ=550 MeV ,mω=783 MeV ,mρ=763 MeV and mδ=983 MeV .The ratios of coupling constants between hyperons and nucleons can be expressed xi=giH/gi,i=σ,ω,ρ and δ.Their values x ωB and xσB , xδB , xρB are 0.783 and 0.7,respectively [49].

表2 饱和核物质性质,饱和密度值以及在饱和密度处对称能、对称斜率和不可压缩系数值[49]Table 2.Properties of nuclear saturation density,namely,the values of the nuclear saturation density ρ0,the symmetry energy Esym,the symmetry energy slope L and the incompressibility Kv [49].

图1给出了6 种情况下星体物态方程.从图1中可以看出,传统中子星和超子星的压强均随着能量密度的增加而增加;在中低密度区域,δ 介子出现后使传统中子星和超子星物态方程均变硬;在高密度区域,δ 介子出现使星体物态方程均变软.在相同质量下,与传统中子星物态方程相比超子星物态方程明显变软,其中在包含Σ 超子的超子星物态方程情况5)和情况6)最为明显.

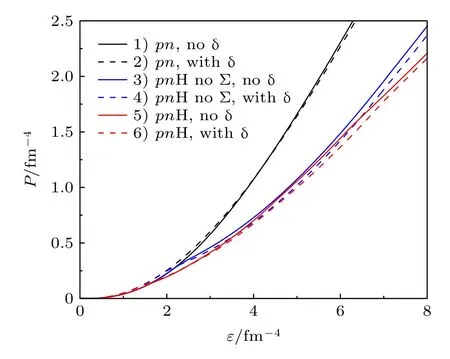
图1 6 种情况下,星体物态方程Fig.1.Equation of states for neutron star matter in the six cases.

图2 给出了6 种情况下星体质量-半径关系.图中阴影区域分别表示PSRs J1903+0327 和J0453+1559 的质量测量值,橙色误差棒表示中子星内部成分探测器公布的孤立中子星PSR J0030+0415 的质量、半径测量值.从图2 中可以看到,δ 介子出现使得相同质量的传统中子星和超子星半径均增大,然而这一改变随着星体质量的增加逐渐减弱;这是由于在中低密度区域δ 介子使星体物态方程变硬,导致在相同质量下含δ 介子的星体半径更大;在高密度区域δ 介子会使星体物态方程变软,导致在相同质量下含δ 介子的星体半径变大幅度减小.对于较小质量的星体,由于其内部没有生成超子,因此传统中子星与超子星质量-半径关系重合;随着星体质量的增加,不同种类的超子开始在星体内部陆续出现形成超子星,相同质量下超子星半径要明显小于传统中子星半径,并且超子星最大质量明显小于传统中子星最大质量.表3 中给出了6 种情况下星体最大质量对应的半径、勒夫数和潮汐形变因子以及最大半径对应的质量、勒夫数和潮汐形变因子.从图2 和表3 可以清晰地看到,6 种情况下星体的最大质量变化较大,其中含有δ 介子的传统中子星即情况2)的最大质量最大,其值可以达到2.119 M⊙;而含有δ 介子的超子星即情况6)最大质量最小,其值为1.691 M⊙;情况1)—情况5) 中最大半径星体对应的都是传统中子星,仅在情况6) 时最大半径星体对应的是含有Σ 超子的超子星.此外,6 种情况下的质量-半径关系均与PSRs J1903+0327 和J0453+1559 的质量测量值以及孤立中子星PSR J0030+0415 的质量、半径测量值符合良好.

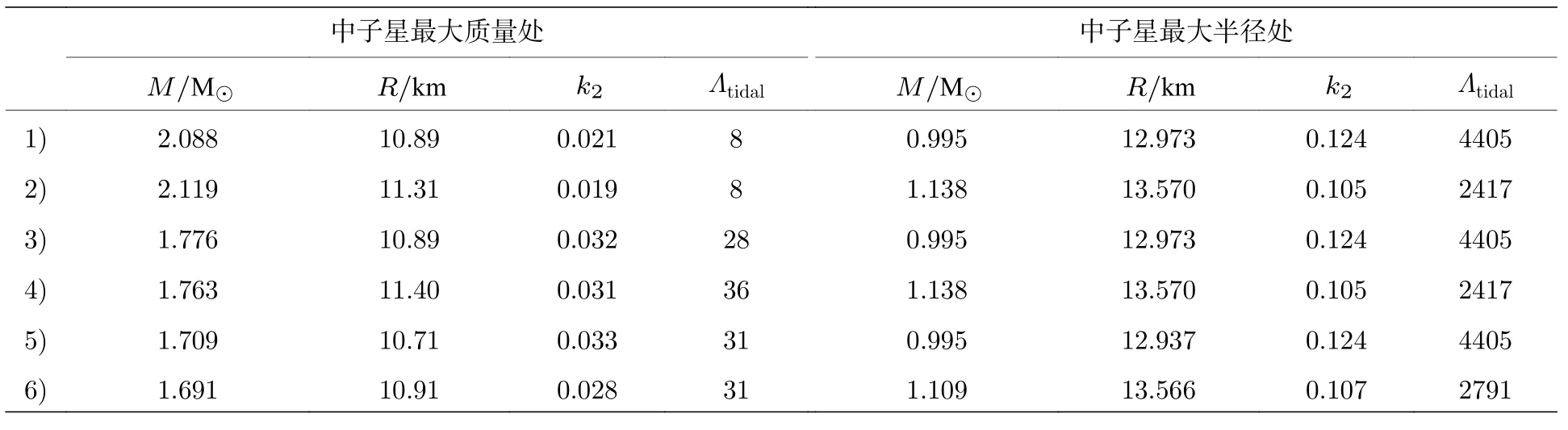
表3 6 情况下,星体最大质量及其对应的半径、勒夫数和潮汐形变因子;星体最大半径及其对应的质量、勒夫数和潮汐形变因子Table 3.Values of the maximum masses M and the corresponding radii R,the tidal Love numbers k2 and the tidal deformabilities Λtidal.Values of the maximum radii R and the corresponding masses M,the tidal Love numbers k2 and the tidal deformabilities Λtidal with the six cases.

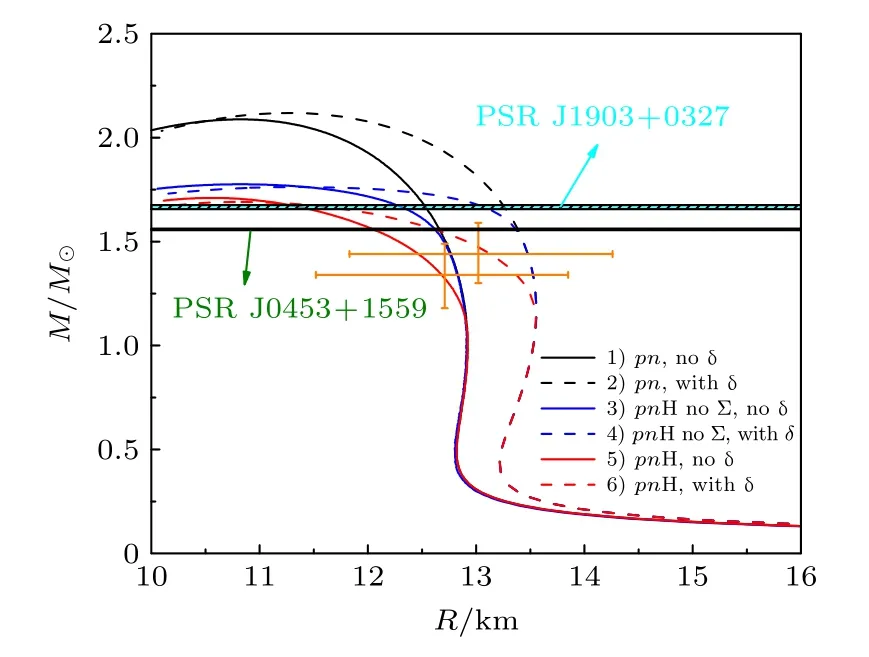
图2 6 种情况下,星体质 量-半 径关 系.不同颜色条纹区域分别表示PSRs J1903+0327 和J0453+1559的质量测量值 和 M⊙ [50,51],橙色误差棒表示PSR J0030+0415 的质量和半径测量值范围,其质量测量值为M⊙ 和 M⊙,相应半径值为km 和 km[52]Fig.2.Mass -radius carves for the six equation of states.The striped areas of different colors stand for the constraints inferred from PSRs J1903+0327 and J0453+1559,and their mass measurement values are M⊙ andM⊙[50,51],respectively.The orange error bars express the constraints on the mass-radius limits of PSR J0030+0451,and its mass measurement values areM⊙ and M⊙,the corresponding radius values are km and km,respectively [52].

图3 给出了6 种情况下星体勒夫数-质量关系.其中黑色虚线表示当星体质量取1.4 M⊙时勒夫数理论值区间,阴影区域分别表示PSRs J1903+0327 和J0453+1559 的勒夫数理论值区间.从图3中可以看出,对于中小质量星体,δ 介子会使得相同质量的传统中子星(或超子星)勒夫数减小;但是,随着星体质量的增加,δ 介子对星体勒夫数的抑制作用逐渐减弱.从图3 还可以看出,超子的陆续出现会抑制星体勒夫数,并在包含Σ 超子的超子星即情况5)和情况6)下表现最为明显.

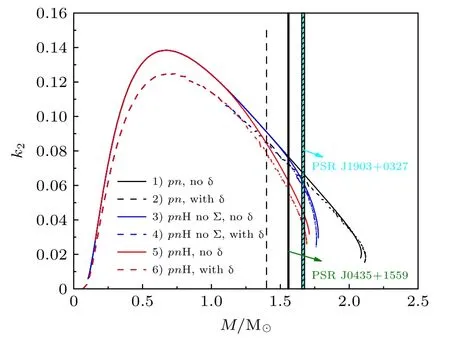
图3 6 种情况下,星体勒夫 数-质 量关 系.其中不同颜色条纹区域分别表示PSRs J1903+0327 和J0435+1559 的勒夫数理论值范围,黑色虚线表示星体质量取 1.4M⊙ 时勒夫数理论值Fig.3.Tidal Love numbers as a function of the masses for the six equation of states.The striped areas of different colors stand for the theoretical values ranges of the tidal Love numbers for PSRs J1903+0327 and J0435+1559,respectively.The vertical dashed line indicates as M=1.4 M⊙ .

图4 给出了6 种情况下星体潮汐形变因子-质量关系.阴影区域分别表示PSRs J1903+0327 和J0453+1559 潮汐形变因子理论值范围,彩色误差棒分别表示引力波信号GW170817 和GW190814对星体潮汐形变因子的约束范围.从图4 可以看到,对于中小质量的星体,δ 介子使得相同质量的传统中子星(或超子星)潮汐形变因子变大;随着星体质量的增加,δ 介子对星体潮汐形变能力影响逐渐减弱,特别是含有δ 介子的大质量超子星潮汐形变能力弱于不含δ 介子的超子星;这是由于星体潮汐形变能力对于半径五次方和勒夫数一次方依赖,如(26)式所示.从图4 中还可以看到,随着星体质量的增加超子陆续出现,使得超子星潮汐形变因子要小于传统中子星潮汐形变因子,在包含Σ 超子的超子星即情况5)和情况6)下表现最为明显;这是因为在相同质量下含有超子的星体半径和勒夫数均减小,如图2、图3 和(26)式所示.表4 中列出了六种情况下1.4 M⊙中子星、PSRs J1903+0327 和J0453+1559 半径、勒夫数、潮汐形变因子的理论值.此外,在本文所选参数下含有δ 介子的传统中子星和超子星潮汐形变因子均满足GW190814 天文观测约束;但是,仅含有Λ,Σ和Ξ 超子的超子星才能同时满足引力波信号GW190814 和GW170817 的天文观测约束;可见,含δ 介子的超子星其内部不同的超子种类对于人们理解星体潮汐形变性质至关重要.相信未来将有更多与中子星相关的引力波数据可用于进一步限制中子星物态方程和潮汐形变性质,这将有助于完善中子星理论模型并揭示星体内超子的种类.

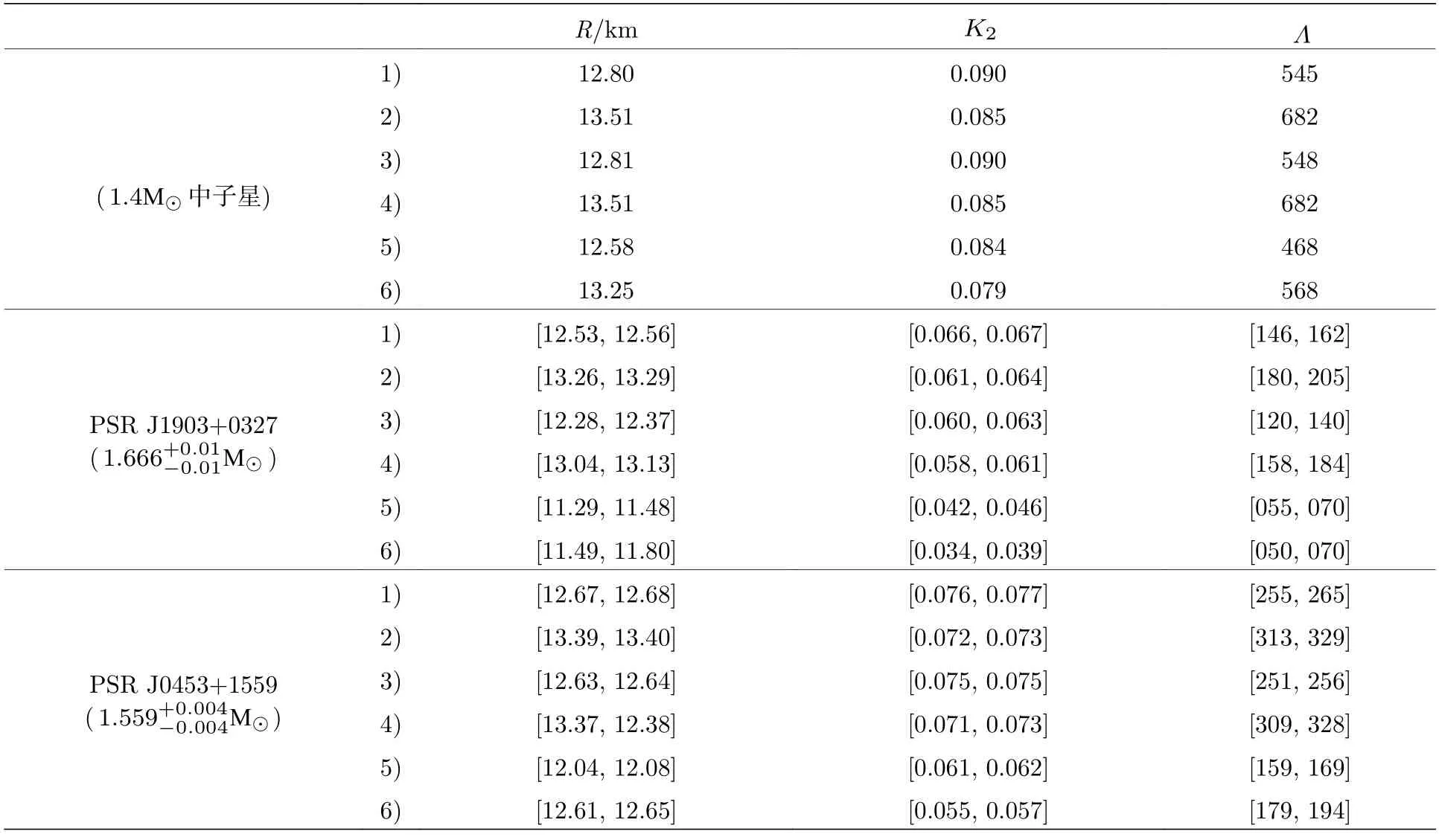
表4 6 种情况下,1.4 M⊙ 中子星、PSRs J1903+0327 和PSR J0453+1559 半径、勒夫数和潮汐形变因子的理论值Table 4.Theoretical values for the radii,the tidal Love numbers and the tidal deformabilities for the 1.4 M⊙ neutron star,PSRs J1903+0327 and J0751+1087,respectively.

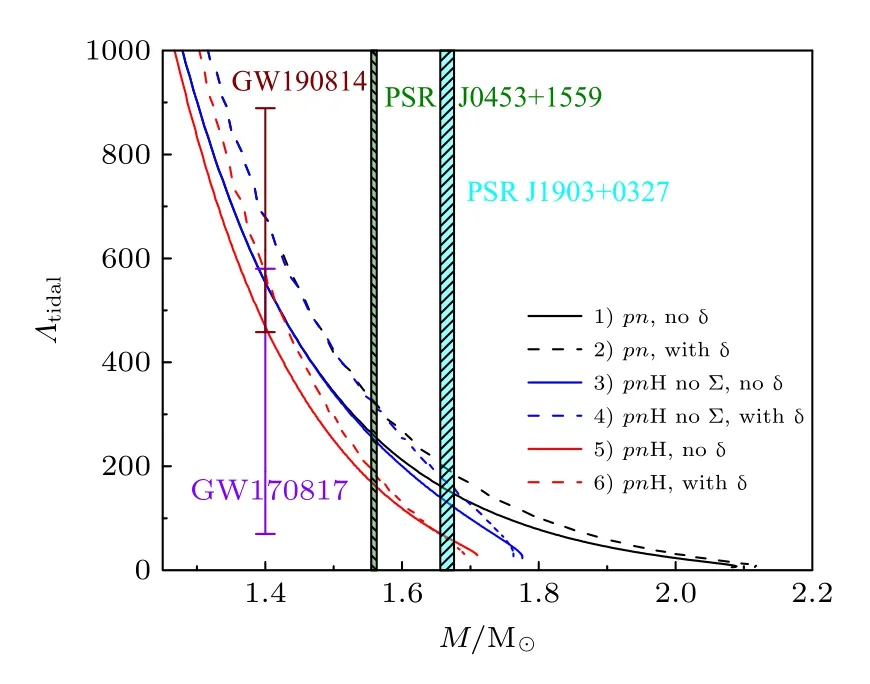
图4 6 种情况下,星体潮汐形变因子-质量关系.不同颜色条纹区域分别表示PSRs J1903+0327 和J0453+1559 脉冲星的潮汐形变因子理论值范围,彩色误差棒分别表示GW170817 和GW190814 对于星体潮汐形变的约束Fig.4.Tidal deformabilities as a function of the masses for the six equation of states.The different colors striped areas stand for the theoretical values of the tidal deformabilities for PSRs J1903+0327 and J0751+1087,respectively.The color error bar expresses the constraints from GW170817 and GW190814 events for the tidal deformabilities.

4 结论

本文在相对论平均场理论框架下研究了同位旋矢量-标量介子δ 对传统中子星和超子星质量、半径、勒夫数和潮汐形变因子的影响.结果表明,对于中小质量星体,δ 介子出现使得星体半径变大、勒夫数减小和潮汐形变能力变强;随着星体质量的增加,δ 介子对星体半径、勒夫数和潮汐形变能力影响逐渐减弱;特别是对于大质量超子星,含有δ 介子的大质量超子星潮汐形变能力弱于不含δ 介子的超子星.此外,超子星中超子的陆续出现会明显的降低超子星最大质量、勒夫数和潮汐形变能力.对于含有δ 介子的星体,仅同时含有Λ,Σ 和Ξ 超子的超子星可以满足两个引力波信号GW190814和GW170817 的天文观测约束,这也许可以作为超子星内含有Σ 超子的一个理论参考.未来人们将获得更多中子星质量、半径和引力波探测数据,将有助于进一步限制中子星物态方程,这将对揭示中子星内部物质成分非常有益.

在本文中,虽然我们的数值结果能够清晰的反映δ 介子对传统中子星(超子星)潮汐形变能力的影响,但仍然存在许多不足之处,比如该数值结果对模型和参数具有依赖性,在模型中我们也没有考虑如σδ2和σ2δ2等介子之间复杂的相互作用.因此,后续我们会根据这些不足之处开展更加深入的研究.

感谢中国科学院国家天文台韩金林研究员和南开大学胡金牛教授的讨论与帮助.