基于UG表达式的参数化曲线建模

陈兵，胡银芬

（惠州城市职业学院，广东 惠州 516025）

0 引言

UG 是Unigraphics的简称，由美国UGS公司开发的一款强大的CAD软件，后来被Siemens PLM Software公司所收购，UG软件以其强大的功能、先进的技术，目前已成为独具特色的CAD/CAM/CAE软件，该软件广泛应用于制造业，如汽车、轮船、机械、模具，以及消费市场的家电、玩具等行业。

来自Siemens PLM Software的NX软件使企业能够通过新一代数字化产品开发系统实现向产品全生命周期管理转型的目标。Unigraphics NX的功能强大，可以让设计师轻松实现各种复杂实体及造型的建构。UG作为目前使用广泛的三维建模软件之一，其参数化建模功能非常强大，参数化建模功能是UG软件的重要功能之一。参数是UG参数化建模的核心要素。在一个复杂实体或造型中，实体的参数是通过“尺寸”来实现建模的。而参数化建模的最主要优点在于其可以通过改变实体的参数来实现快速及方便的产品设计修改。在参数化建模中，表达式是参数化建模中的一项重要内容，它表现了参数之间彼此制约的“并联”联系。本文以一个果盘的造型为例，详细讲述基于UG NX12.0表达式的参数化曲线曲面建模。基于UG的表达式（方程式）的参数化曲线的功能，来实现果盘的参数化曲面建模。通过UG的参数化表达式生成的曲线具有相连性，表达式的参数变化时，曲线也会随着变化，所关联的三维实体模型也会随着表达式的变化而变化。这种基于UG表达式的参数化曲线建模方法，用参数化表达式（方程式）的方法来定义曲线、曲面及实体的各个尺寸间的约束关系，摆脱了传统的由点、线、面的各尺寸为主的建模方式。表达式的参数化曲线建模方法大大减轻了设计工程师的繁琐劳动，同时为产品系列化的设计、生产等节约了宝贵的时间，提高了产品的设计效率，降低了开发周期与生产成本[1]。

1 UG参数化建模的方法

UG NX作为强大的三维建模软件，其建模的方式有很多种，包括实体建模、特征建模、参数化建模等。实体建模主要是通过UG软件本身所存储的一些基本体素，通过运用各种布尔运算，生成简单或复杂的三维模型实体。特征建模是通过运用UG建模中的各种特征或其集合来创建三维零件模型的过程。特征是指UG软件本身内部具有特定意义的几何形状，在UG软件中特征主要分为三大类：第一类是基本体素特征；第二类是成型特征；第三类是加工特征。UG的参数化建模，也称为参数化设计。参数化建模的关键是通过尺寸的参数表达式驱动来实现UG三维模型的构建。UG的参数化建模主要是指利用参数化模型的表达式来对各个尺寸进行定义或约束，而不是用某个具体的数值来定义。如果改变其中一个参数值，那么与它有关联的其它尺寸也将会自动随着表达式改变，从而生成新的相同类型的三维模型。表达式的尺寸驱动是参数化设计的关键[2]。

UG的参数化建模一般有3种方法：

1）第一种方法是基于表达式（方程式）的参数化实体建模。基于表达式（方程式）的参数化实体建模主要是将模型的各个参数通过指定函数关系式（方程式）来表达。通过把参数定义为具体的数学公式、三角函数、数字或把几个参数按数学关系通过运算符号连接，使它们产生关联。对模型进行修改时，只需要改变其中一个或几个参数，相应的其他关联参数即可随之改变[3]。

2）第二种方法是基于电子表格进行参数化建模。UG NX可基于电子表格进行参数化建模。电子表格的参数化建模是把模型中的各个尺寸及位置信息一一摘录并输入到电子表格中，然后对参数分别定义，使参数和模型的尺寸及位置信息逐一对应，通过电子表格使模型的参数尺寸与表格中的参数逐一关联对应。

3）第三种方法是基于特征的参数化三维模型设计。UG NX的基于特征的参数化建模设计是将UG中的特征命令（特征建模）和参数化（表达式）建模结合起来，主要是将参数化设计的方法用到特征建模中去，用参数驱动或变量设计的方法实现模型的参数化建模。

2 UG典型表达式介绍

UG NX软件的表达式可以根据需要输入，并生成所需要的曲线。表达式的形式多种多样，数学模型中较为典型的有螺旋曲线表达式（如表1）、圆形波浪曲线（蝶形曲线）表达式（如表2）等[4]。

1）假如圆柱螺旋线半径r为20 mm，螺距p为6 mm，圈数n为6，则表达式如表1所示。

表1 螺旋曲线表达式

把上述公式输入UG表达式后，利用“规律曲线”中的根据方程创建的螺旋曲线如图1所示。

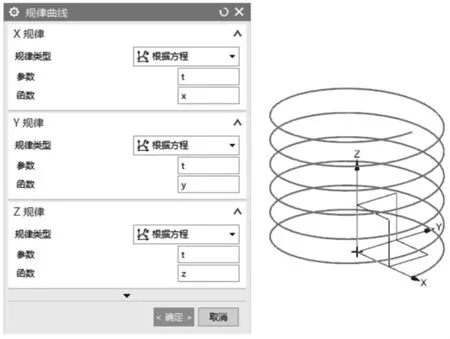
图1 根据表达式创建的螺旋曲线

2）假如圆柱螺旋线半径r为40 mm，波浪线的振幅为6 mm，波峰的数量为10，则表达式如表2所示。

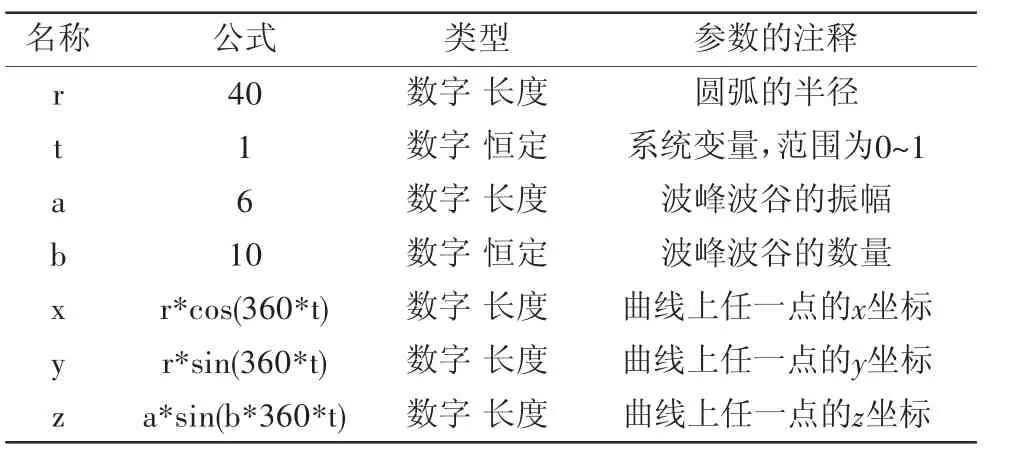
表2 圆形波浪曲线表达式

把上述公式输入UG表达式后，利用“规律曲线”中的根据方程创建的圆形波浪曲线如图2所示。

图2 圆形波浪曲线（蝶形曲线）

以上仅列举了2种较为典型的表达式的参数化曲线，在UG的建模设计中，可以根据需要输入所要创建的曲线方程来构建特殊复杂的曲线。

3 果盘的参数化设计

图3所示为果盘的模型图样，由图3可知果盘的边沿是一个起伏的形状，有24个波峰和波谷，虽然果盘的整体造型不复杂，但是如果按普通的建模方法构建果盘的边沿，就很难把24个起伏的波浪形状建模出来，所以在果盘的三维建模中，为了准确快捷地创建好盘沿的起伏形状，必须采用表达式的参数化设计，利用表达式构建起伏的波浪曲线。

3.1 果盘边沿曲线的参数表达式

由图3可知，果盘的盘沿是圆形的正弦曲线，有24个波峰波谷，正弦曲线的振幅为5 mm，由此可以确定圆形的正弦曲线各参数的名称和公式，如表3所示[5]。

表3 果盘圆形正弦曲线各参数的名称和公式

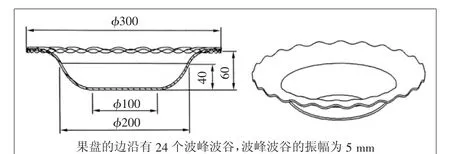
图3 果盘模型图

公式解析：r是指圆弧的半径，由图1可知直径为300，所以半径为150 mm。t是系统变量，一般取1。X、Y、Z分别代表正弦曲线上各点的X、Y、Z坐标值。其中在5*sin(24*360*t)+60中，“5”是圆形正弦曲线的振幅，“24”表示有24个正弦波，“60”代表的是正弦波上与XOY基准平面的距离。

3.2 果盘参数化建模

打开UG NX12.0，进入建模模式后，点击UG NX12.0的菜单栏“工具”→“表达式”，弹出“表达式”对话框，然后在表达式中输入表1所示的全部公式，输入完成后如图4所示。

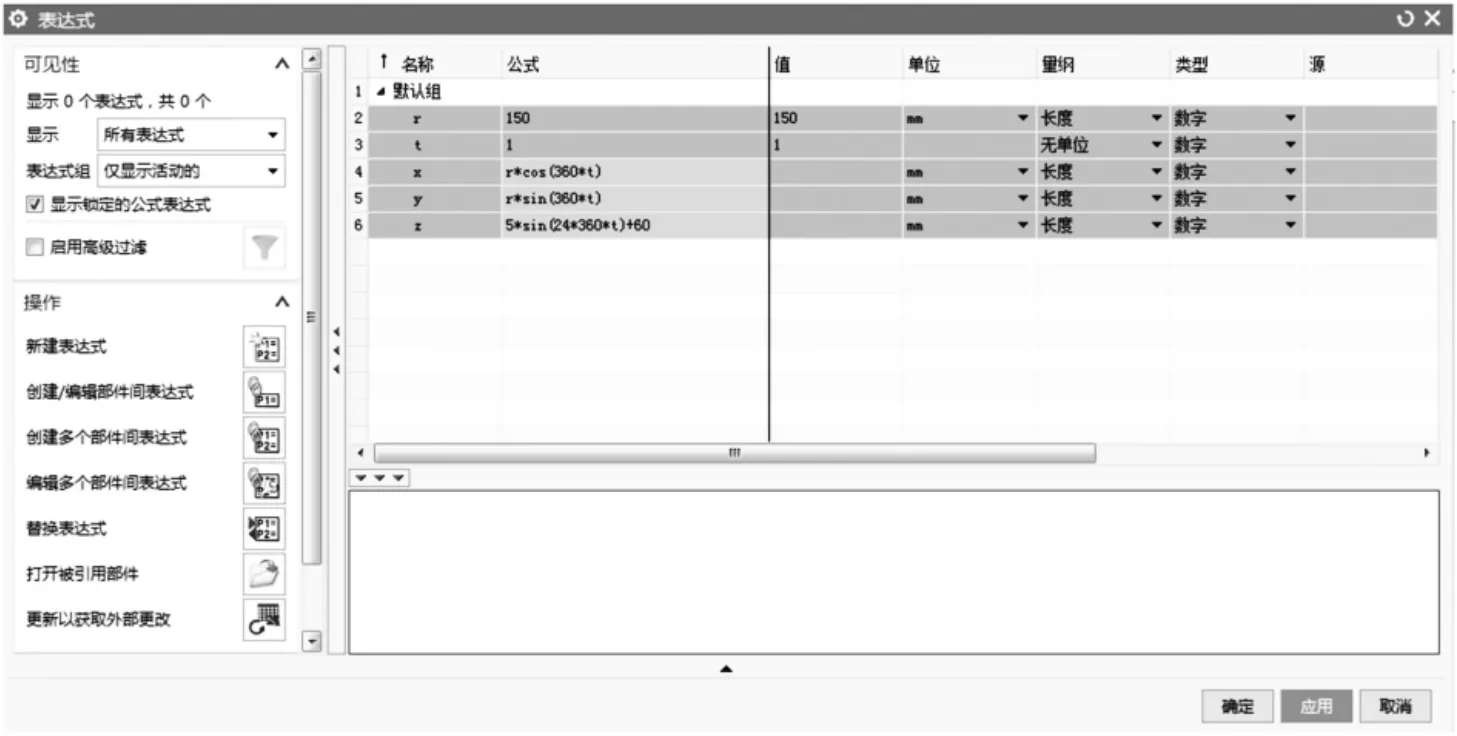
图4 圆形正弦曲线表达式参数方程输入

表达式参数方程输入完成后，即可利用规律曲线创建果盘的上部圆形正弦曲线。在UG NX12.0建模环境中点击“菜单”→“插入”→“曲线”→“规律曲线”，弹出规律曲线的创建，此时即可预览到将要创建的规律曲线，如图5所示，点击确定即可完成创建。

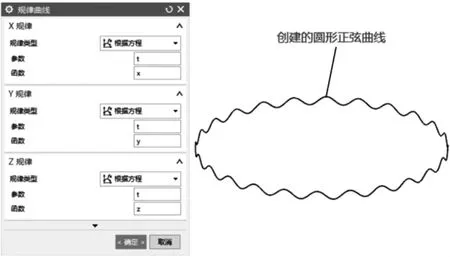
图5 创建规律曲线

创建完成规律曲线后，果盘的其他曲线创建就相对简单，依次创建好φ100和φ200的圆，然后利用曲面造型功能的有界平面、通过曲线组等功能命令创建曲面，曲面创建完成后，利用片体加厚，即可完成果盘的整体造型，创建的过程及结果如图6所示。

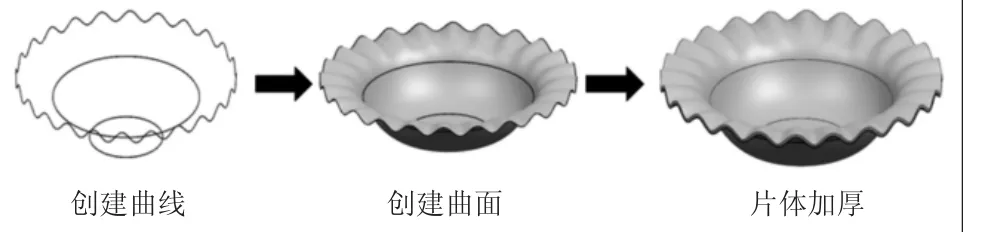
图6 果盘建模过程及结果

果盘的盘沿造型过程中，利用UG的表达式参数化建模可以快速创建出所需要的曲线，然后再通过曲线曲面建模，快速地对果盘的造型进行设计，有效提升了设计效率。同时还可以对果盘的参数进行不同的更改或导入不同的部件族，那么就可以修改不同的参数得到大小及起伏不一样的果盘造型。

4 结论

对于波浪形曲线，在UG中用一般的方法是很难创建出来的，因此在一些产品如果盘、盘子或其他的一些艺术产品设计过程中，为了设计出客户需要的形状，只能利用UG强大的表达式参数化功能，只需把所要构建的曲线方程输入到表达式中，然后利用UG的规律曲线（基于UG表达式的参数化方程），即可快速创建出所需要的复杂曲线。而且对于类似的曲线或形状，只要改变方程的某些参数，即可对曲线的大小、起伏数目等进行更改。

基于UG表达式的参数化曲线画法实现了波浪形的果盘的参数化建模，实现了每个参数之间的关联与约束。当其中某个特征参数发生了变化，则其对应的特征的几何形状也随着表达式的参数改变而改变。这种基于UG表达式的参数化曲线建模的方法可应用于所有相似类型的特殊曲线的建模，只要创建相应的表达式参数化方程，即可实现复杂曲线的参数化设计和建模。本文中的果盘设计方法不仅大大缩短了果盘的设计周期，提高了设计效率，同时为系列化设计节省了修改的时间，并为其他复杂曲线曲面实体的设计和建模提供了借鉴，具有很好的实用性[6]。

因此利用UG强大的表达式参数化进行复杂曲线创建，可以快速地创建出复杂多样的曲线，在一些曲线或曲面复杂的实体建模中可以快速且精确地创建出来，同时有利于后期对几何模型进行修改，大大提高设计效率和制造质量，从而使得产品的设计制造周期缩短并更快上市。