两级星型齿轮传动系统低振动齿廓修形设计研究

张雪强， 赵书樊， 郭丽君， 侯祥颖， 李政民卿

（1.中国航空工业集团公司金城南京机电液压工程研究中心，南京 211106；2.航空机电系统综合航空科技重点实验室，南京 211106；3.南京航空航天大学机电学院，南京 210016）

0 引言

齿轮传动因其在高速重载下的振动和冲击极为明显，因而齿轮系统振动性能优化成为诸多学者关注的问题。齿廓修形是指通过对齿廓曲线的微量切削，降低啮合冲击，减少由于变形或误差等因素引起的啮合偏差，提升传动质量与性能，成为目前最有效的抑振手段之一，也受到学者的广泛关注。

C. J. Bahk等[1]建立了行星齿轮传动系统动力学分析模型，利用摄动法研究了齿廓修形参数对系统振动特性的影响，并以动态传递误差波动量最小为目标确定了系统齿廓修形参数；M. Chapron等[2]以行星传动系统为对象，基于系统动力学分析模型和遗传优化算法，以降低动态啮合力为目标，得到了系统的优化修形参数。吴勇军等[3]根据斜齿轮沿啮合线方向的变形量，确定了斜齿轮副的齿廓修形参数，并研制了相应的试验件，开展了传动系统的振动对比试验，试验结果如图1所示；汤鱼等[4]以行星齿轮系统传动误差波动量最小为目标，确定了行星齿轮传动系统中各齿轮副的修形参数，并对修形与未修形齿轮副开展了动力学分析与试验研究，验证了修形方法的有效性；王成等[5]建立了单级齿轮传动系统非线性动力学模型，形成了考虑齿廓修形参数的啮合刚度计算方法，并建立了以系统动载系数最小为目标的齿廓修形设计方法；严岳胜等[6]针对星形齿轮传动系统，研究了计入齿廓修形参数的承载传动误差的计算方法，并以承载传动误差幅值最小为目标，开展了系统齿廓修形优化设计研究。吕世恒等[7]针对星型传动系统提出了耦合振动边界条件和动力学分析模型，讨论了支撑刚度变化对系统振动的影响规律。

从上述文献可知，国内外学者在齿廓修形原理、加工方式、齿轮副齿廓修形设计方法等方面已开展了大量研究。但目前针对两级星型齿轮传动系统的齿廓修形设计方法研究较少，在实际应用中缺乏理论支撑；因此，需要针对两级星型齿轮传动系统开展齿廓修形设计方法研究。

1 两级星型齿轮传动系统齿廓修形设计方法

1.1 考虑齿廓修形的两级星型齿轮传动系统动力学模型

两级星型齿轮传动系统结构如图1（a）、图1（b）所示，太阳轮为输入级，星型轮2与太阳轮啮合，星型轮3与星型轮2为双联齿轮，并与内齿圈啮合，内齿圈为输出级。基于齿轮系统构型和动力学分析基本理论可以建立两级星型齿轮系统动力学模型，如图1（c）所示。

图1 两级星型齿轮结构示意图及动力学建模

根据齿廓修形原理，将主、从动轮齿廓修形量考虑到啮合线方向的相对位移中，易得啮合线方向位移为

式中：rp、rg分别为主、从动轮基圆半径；θp、θg、lp1、lp2、lg1、lg2分别为主动轮扭转角位移、从动轮扭转角位移、主动轮两端轴承节点处x方向振动位移、主动轮两端轴承节点处y方向振动位移、从动轮两端轴承节点处x方向振动位移、从动轮两端轴承节点处y方向振动位移；l1、l2分别为齿轮到两轴承支点的距离；e为齿轮副的准静态传递误差；Δp、Δg分别为主、从动齿轮在啮合点处对应的修形量。

根据式（1）将齿廓修形量与齿轮副的准静态传递误差相互组合，两级星型齿轮传动系统考虑齿廓修形参数的的准静态传递误差为：

式中：Δ1、Δ4分别为太阳轮与内齿圈在啮合点处对应的修形量；Δ2i、Δ3i分别为第i支路星型轮2与星型轮3在啮合点处对应的修形量；下标i表示不同支路（i=1，2，3）。根据两级星型齿轮传动系统啮合位置关系（如图1（c）所示），获得啮合线方向的位移为：

式中：xMn1-2i、xMn4-3i分别为外齿轮副、内齿轮副啮合线方向位移；MSTE1-2i、MSTE4-3i分别为外齿轮副、内齿轮副准静态传递误差；下标i表示不同支路（i=1，2，3）。容易得到考虑齿廓修形的两级星型齿轮传动系统动力学模型：

式中：m1、m2i、m3i、m4分别为太阳轮、星型轮2、星型轮3与内齿圈的质量；I1、I2i、I3i、I4分别为太阳轮、星型轮2、星型轮3与内齿圈的转动惯量；T1、T2分别为太阳轮和内齿圈的转矩；c1-2i、c4-3i分别为外齿轮副、内齿轮副间的啮合阻尼；k1-2i、k4-3i分别为外齿轮副、内齿轮副间的啮合刚度；ki、ci分别为双联齿轮当量扭转刚度、当量扭转阻尼；FMd1-2i、FMd4-3i分别为外齿轮副、内齿轮副动态啮合力；下标i与前文意义相同，αw、αN分别为外齿轮副、内齿轮副啮合角。

1.2 两级星型齿轮传动系统低振动齿廓修形设计分析方法

两级星型齿轮传动系统主要由太阳轮、多个双联星轮及内齿圈等多种零部件组成，其中太阳轮与星型轮2构成外啮合副，星型轮3与内齿圈构成内啮合副，而齿廓修形主要针对一对齿轮副。因此，需要针对两级星型齿轮传动系统中内、外啮合副分别开展齿廓修形设计分析。基于圆柱齿轮副齿廓修形设计分析方法，针对两级星型齿轮系统，建立了考虑齿廓修形的传动系统级数学模型。

众所周知齿廓修形有最大修形量、修形长度和修形曲线三要素。其中修形曲线可表示为包含3个系数的函数，共需要用5个参数表示一个齿轮的修形参数，而3支路的两级星型齿轮传动系统共存在8个齿轮，如若将所有齿轮的修形参数均列为设计变量，将大大增加问题的复杂度。为简化设计过程，本文认为同级齿轮副修形参数一致；并且考虑内齿圈齿廓修形加工难度以及工况等因素，仅选择内、外齿轮副的主动轮（太阳轮、星型轮3）进行修形设计，而星型轮2与内齿圈则不作修形处理。因此，两级星型齿轮传动系统齿廓修形设计的设计变量为

式中：Δmax1、Δmax3分别为太阳轮与星型轮3的最大修形量；L1、L3分别为太阳轮与星型轮3的修形长度；a1、b1、c1与a3、b3、c3分别为太阳轮与星型轮3修形曲线的相关系数。

本文所建立的齿廓修形设计分析方法主要针对原有的两级星型齿轮传动系统，忽略齿轮系统设计过程中的干涉约束、齿数选择约束等，仅考虑齿廓修形参数相关的约束。为此，本文定义了两级星型齿轮传动系统齿廓修形设计的约束条件，最大修形量的边界约束：1）Δsetmin≤Δmax≤Δsetmax。Δmax为最大修形量；Δsetmin、Δsetmax分别为最大修形量自定的边界值。2）保证修形长度应不大于双齿啮合区长度的修形长度的边界约束，即Lsetmin≤L≤Lsetmax。L为修形长度；Lsetmin、Lsetmax分别为修形长度自定的边界值，其中Lsetmax不大于双齿啮合区长度。3）齿轮副的弯曲疲劳强度与接触疲劳强度约束为SF≥［SF］，SH≥［SH］。SF、SH分别为齿轮副的弯曲、接触疲劳安全系数；［SF］、［SH］分别为齿轮副的弯曲、接触疲劳的许用安全系数。

两级星型齿轮传动系统由于受到制造误差、安装误差、构件的弹性变形等因素的影响，存在各支路间载荷分配不均匀的现象。因此，同级齿轮副不同支路间动态啮合力的齿频幅值存在一定差异；为简化两级星型齿轮传动系统修形设计过程，本文以同级齿轮副中各支路动态啮合力齿频幅值的最大值，表示该级齿轮副动态啮合力的齿频幅值，即

式中：AF为同级齿轮副动态啮合力的齿频幅值；Ai（i=1，2，…，n）为第i支路同级齿轮副齿频幅值。

为同时保证内外两级齿轮副的振动抑制效果，结合圆柱齿轮副中以动态啮合力啮合齿频幅值最小为目标的设计方法，建立如下目标函数：

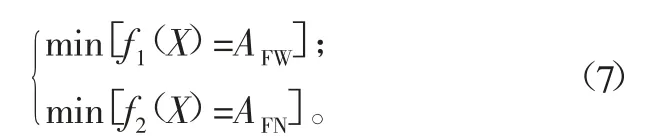
式中，AFW、AFN分别为外、内齿轮副动态啮合力的齿频幅值。

由上述分析可知，两级星型齿轮传动系统齿廓修形设计是一个双目标的设计问题，理论上期望两个目标函数都达到最优，但实际分析过程中，两个目标函数往往无法同时达到最优。因此，双目标的设计问题关键是寻找到能接受的非劣解[8]。为此，本文采用设计变量联合变化的方式，分别计算两级星型齿轮传动系统内外齿轮副的齿频幅值，通过与未修形的分析结果对比，寻找齿廓修形参数的非劣解，最终从非劣解集合中寻找较好的非劣解。基于上述分析思路，形成了两级星型齿轮传动系统齿廓修形设计分析流程，如图2所示。

图2 两级星型齿轮传动系统齿廓修形设计分析流程

2 齿廓修形参数对两级星型齿轮系统动态性能影响规律分析

2.1 系统动态啮合力齿频幅值规律

1）外齿轮副直线修形对系统动态力齿频幅值的影响规律。

本次分析采用外齿轮副直线修形，内齿轮副不修形的修形方案，并选取最大修形量与修形长度联动变化，开展系统动态啮合力分析。根据外齿轮副受载情况以及修形长度选取的相关经验[9]，本文选取外齿轮副最大修形量范围为［0，20 μm］，修形长度占比范围为［0.5，1］。其中，系统内、外齿轮副动态啮合力齿频幅值的变化规律如图3所示。

图3 外齿轮副直线修形对系统动态力齿频幅值的影响

由图3可知，在大部分修形参数下，系统内外齿轮副动态啮合力的齿频幅值均有不同程度的下降，相比于内齿轮副，对外齿轮副动态啮合力齿频幅值的抑制作用更为明显；当修形长度保持不变时，随着最大修形量的增加，外齿轮副动态啮合力最大齿频幅值出现先减小、后增大的现象，而内齿轮副动态啮合力最大齿频幅值变化不大。

2）外齿轮副抛物线修形对系统动态啮合力的影响规律。

本次分析选择外齿轮副抛物线修形，内齿轮副不修形的修形方案，并保证其余参数分析范围不变；利用前述分析方法，开展系统动态行为分析，获得系统内、外齿轮副动态啮合力齿频幅值的变化规律，如图4所示。

图4 外齿轮副抛物线修形对系统动态力齿频幅值的影响

对比外齿轮副直线修形对系统动态力的影响规律，结合图3可知，修形曲线的改变，对系统动态啮合力齿频幅值的变化趋势影响不大，主要影响了最大修形量、修形长度及最大齿频幅值的具体数值；相比于直线修形分析结果，在当前设计参数下，外齿轮副选取抛物线修形对系统动态啮合力齿频幅值的抑制作用更佳。

3）内齿轮副直线修形对系统动态啮合力的影响规律。

本次分析采用内齿轮副直线修形，外齿轮副不修形的修形方案，并选取最大修形量与修形长度联动变化。由于内齿轮副受载情况比外齿轮副更大，其最大修形量分析范围应大于外齿轮副。因此，本文选取内齿轮副最大修形量范围为［0，40 μm］，修形长度占比范围为［0.5，1］。利用前述分析方法，开展系统动态行为分析，获得系统内、外齿轮副动态啮合力齿频幅值的变化规律，如图5所示。

图5 内齿轮副直线修形对系统动态力齿频幅值的影响

由图5可知，内齿轮副修形对内齿轮副动态啮合力最大齿频幅值影响作用大于外齿轮副；当修形长度不变时，随着最大修形量的增加，内齿轮副动态啮合力最大齿频幅值出现先减小、后增大的变化趋势，而外齿轮副动态啮合力最大齿频幅值主要在1186～1188 N之间波动；并且在当前范围内，内齿轮副动态啮合力最大齿频幅值存在最小值点。

4）内齿轮副抛物线修形对系统动态啮合力的影响规律。

本次分析选择内齿轮副抛物线修形、外齿轮副不修形的修形方案，并保证其余参数分析范围不变；利用前述分析方法，开展系统动态行为分析，获得系统内、外齿轮副动态啮合力齿频幅值的变化规律，如图6所示。

图6 内齿轮副抛物线修形对系统动态力齿频幅值的影响

对比内齿轮副直线修形对系统动态力的影响规律，结合图5可知，修形曲线的改变对外齿轮副动态啮合力齿频幅值的变化趋势影响不大，但内齿轮副的最小值点正逐步移动到修形长度与最大修形量更大的区域。对比两种修形曲线的分析结果可知，在当前设计参数下，内齿轮副选取直线修形对系统动态啮合力齿频幅值的抑制作用更佳。

由上述分析可知，在两级星型齿轮传动系统中，对任一级齿轮副采取合理的齿廓修形参数，均可减小系统内外齿轮副动态啮合力齿频幅值，并且对该级齿轮副动态啮合力齿频幅值的抑制作用更加明显。因此，在初选内外齿轮副齿廓修形参数范围时，可仅考虑修形参数对修形齿轮副动态啮合力齿频幅值的影响。为此，针对本次设计参数，给出如下修形方案：

1）针对外齿轮副，采用太阳轮齿顶修形、星型轮2不修形的修形方式，其中最大修形量的取值范围为［10，20 μm］，修形长度占比的取值范围为［0.5，0.7］，修形曲线为抛物线；

2）针对内齿轮副，采用星型轮3齿顶修形、内齿圈不修形的修形方式，其中最大修形量的取值范围为［25，35 μm］，修形长度的取值范围为［0.6，0.8］，修形曲线为直线。

针对上述修形参数，分别选取太阳轮与星型轮3的最大修形量以及修形长度联动变化，基于前文建立的系统级动力学分析模型开展动态分析，获取系统齿廓修形参数的非劣解，如图7所示。

图7 齿廓修形参数非劣解集合

根据上述分析结果，本文选取离原点最近的非劣解作为当前工况下的最佳修形参数，如表1所示。

表1 两级星型齿轮传动系统不同修形参数汇总表

基于上述齿廓修形参数，利用前述分析方法，开展修形齿轮系统的动态行为分析，并与未修形齿轮系统进行对比。其中，动态啮合力对比结果如图8所示，图中fW表示

图8 齿轮副动态啮合力频域对比图

2.2 两级星型齿轮传动系统齿廓修形设计与响应分析

外齿轮副的啮合齿频，fN表示内齿轮副啮合齿频；星型轮横向振动位移对比结果如图9所示。

图9 星型轮横向振动位移对比图

由上述分析结果可知，齿廓修形有效地抑制了内外齿轮副动态啮合力频域幅值，且对齿频处幅值抑制作用最为明显。基于系统动态啮合力，利用前文中动载系数计算方法，可获得未修形齿轮系统外齿轮副动载系数为3.82，内齿轮副动载系数为2.78；而修形齿轮系统外齿轮副动载系数为2.67，内齿轮副动载系数为1.76。对比未修形齿轮系统的动载系数可知，外齿轮副动载系数比未修形齿轮系统下降30.1%，内齿轮副动载系数比未修形齿轮系统下降36.7%；此外，齿廓修形后星型轮的横向振动位移幅值出现了明显的下降。因此，合理的修形参数可以有效地抑制系统动态啮合力，减小系统振动，改善传动性能，且本文所建立的两级星型齿轮传动系统齿廓修形设计方法，可为两级星型齿轮传动系统齿廓修形设计提供理论参考。

3 结语

本文主要针对两级星型传动系统齿廓修形设计方法开展研究，建立了考虑齿廓修形参数的两级星型齿轮传动系统动力学模型，形成了两级星型齿轮传动系统低振动齿廓修形设计方法，开展修形参数对系统动态啮合力齿频幅值的影响规律研究，在此基础上完成了两级星型齿轮传动系统齿廓修形参数的设计，并对比了未修形与修形齿轮系统的动态响应，验证了齿廓修形设计方法的可行性，为两级星型齿轮传动系统齿廓修形设计提供理论依据。

1）仅选择外齿轮副修形，并保持修形长度不变的情况下，随着最大修形量的增加，外齿轮副动态啮合力齿频幅值呈现出先减小、后增大的变化趋势，内齿轮副动态啮合力齿频幅值出现持续减小的变化趋势，但内齿轮副动态啮合力最大齿频幅值变化范围远小于外齿轮副；而修形曲线的改变，对系统内外齿轮副动态啮合力齿频幅值的变化趋势影响不大，主要影响了最大修形量、修形长度及最大齿频幅值的具体数值；针对当前设计参数，外齿轮副选取抛物线修形对系统动态啮合力齿频幅值的抑制作用更佳。

2）仅选择内齿轮副修形，并保持修形长度不变的情况下，随着最大修形量的增加，内齿轮副动态啮合力齿频幅值呈现出先减小、后增大的变化趋势，外齿轮副动态啮合力齿频幅值出现波动变化，并且外齿轮副动态啮合力最大齿频幅值变化范围远小于内齿轮副；当内齿轮副选择直线修形时，在分析区间内存在内齿轮副动态啮合力齿频幅值的最小值点，但改变修形曲线后，内齿轮副齿频幅值的最小值点正逐步移动到修形长度与最大修形量更大的区域；针对当前设计参数，内齿轮副选取直线修形对系统动态啮合力齿频幅值的抑制作用更佳。

3）针对系统任一级齿轮副采取齿廓修形，可同时影响系统两级齿轮副的动态行为，但对本级齿轮副的影响作用远大于另一级齿轮副；因此在初步选取设计区域时，可先仅考虑齿廓修形参数对该级齿轮副动态行为的影响；合理的修形参数可以有效地减小系统的振动，抑制齿轮副间的动态啮合力，降低齿轮副间的动载。