改进的椭圆曲线数字签名方案及实例分析
2023-02-17王昊轩黄林飞
杨 青 王昊轩 梁 磊 黄林飞
(西安航空学院理学院 陕西 西安 710077)
0 引 言
如今计算机科技的进步相当快,同时互联网得到大量运用,全球迈向信息化阶段,人们借助公共网络与信息平台进行交流,因此电子政务与电商,还有互联网平台同样飞速进步,逐步构建信息分享平台。然而个人与公司、国家等各方信息均需保密,例如银行交易与公司财会,还有国家政治与军事等信息。在信息安全系统的性能相对来说较低时,就很容易遇到侵略者,借助资源分享平台来盗取关联信息,以此获取巨大的经济利益,对网络安全形成不小的损害。因而由个人入手,保证信息的安全,已然变成如今工作的要点,也受到整个社会以及国家的高度重视。
数字签名技术是网络环境下的认证技术,该签名技术最早是由Diffie等[1]于1976年提出。在此之后,各类数字签名方案相继被提出,并得到了很大的发展和广泛的应用。然而,基于椭圆曲线的签名算法相对于离散对数签名算法拥有更高的安全性和高效性。Zhao等[2]给出了椭圆曲线认证加密方案的构造方法,方案具有消息恢复的功能。2017年, Chandrasekhar等[3]提出了使用代理签名进行基于云健康信息交换的访问控制。Kumar等[4]提出了可证明安全的基于证书的代理盲签名方案,该方案运用了双线性对。Kumar等[5]提出了一个无证书聚合签名方案,并在随机预言模型下证明方案的安全性。Xuan等[6]提出了一种新的数字签名方案,该方案是基于求解根问题和一些扩展根问题的困难性。根据不同的密码体制,Shuai等[7]提出的方案采用Rabin密码体制,避免了口令验证表的存在。Seo[8]提出的签名方案是基于RSA密码体制的,并在准模型下验证该方案。根据不同的实际需求,学者们分别提出了各种数字签名方案。比如,欧海文等[9]提出群签名方案,李亚红等[10]提出门限签名,杨小东等[11]提出无证书签名方案。本文仔细研读并分析文献[2,5,8-9]后提出改进的基于椭圆曲线密码体制的数字签名方案,改进的方案能够防御生日攻击,提高数字签名的安全性能,而且运算量不大。
1 数字签名的模型
数字签名方案的组成部分可以分为三个环节,分为系统初始化过程、签名产生过程、签名验证过程,下面就数字签名的形式加以说明:
(1) 初始化过程。数字签名产生过程中,涉及到基本参数的问题,为(M,S,K,Sig,Ver)其含义各不相同,按顺序分别为消息集合、签名集合、密钥集合(PK为公钥集合,SK为私钥集合)。Sig代表的是签名产生算法集合,Ver代表的是签名验证算法集合。
(2) 签名产生过程。K为密钥集合,在对签名进行计算时,其算法为Sigsk∈Sig,Sigsk:M→S,m∈M作为任意消息,s=Sigsk,s∈S为消息m的签名,将(m,s)发送给签名验证者进行验证。
(3) 签名验证过程。以密钥集合K为例,下式为相应的签名验证算法。
Verpk:M×S→{True,False}
Verpk(m,s)=True,s=Sigsk(m)
Verpk(m,s)=False,s≠Sigsk(m)
当(m,s)被签名验证者接收到后进行计算,如果Verpk(m,s)=True,说明签名是具有效力的,反之无效。
2 椭圆曲线数字签名方案
椭圆曲线参数的含义如表1所示。
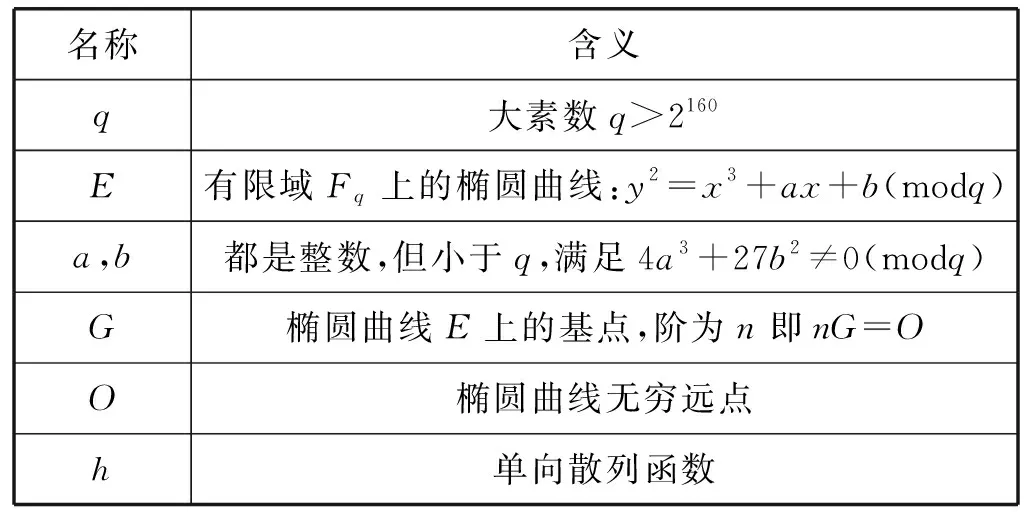
表1 椭圆曲线参数的含义
2.1 Zhao等[2]的数字签名方案
Zhao等[2]给出了一个基于椭圆曲线密码体制的具有消息恢复功能的认证加密方案,该方案由以下几个过程组成,分别为初始化过程、签名的产生过程、验证签名和消息恢复。
1) 初始化过程。用户A的私钥为KA,对应公钥为PA=KAG;用户B的私钥为KB,对应公钥为PB=KBG。
2) 签名的产生。
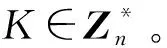
(2)A计算R=KPB=(x,y),r=h(x)-1m(modn),若r=0则返回(1)。
(3) 计算s=K+rKA(modn),若s=0,则返回(1)。
(4) 消息m的签名:(r,s)。
3) 验证签名和消息恢复。B接收到签名(r,s),下载域参数及A的公钥,并进行计算。
(1) 检验r、s是否在区间[1,n-1]上,如果不在此区间则拒绝签名。
(2) 计算X=sG-rPA=(x′,y′)和m=h(KBx′)r(modn)为消息恢复方程。
(3) 若X=0,B拒绝接受签名,否则B计算原始消息m,并对消息进行检验,如果正确,则接受签名,反之拒绝。
在消息末尾加中冗余位被广泛采用,其方法有多种,可以把参与者的身份进行认证,或采用被通信双方指定的字符串,B拥有的私钥是保密的,没有人能够对消息进行恢复操作,也不可能知道消息是由谁发出的,但是B有此权限,能够对原始消息进行计算,掌握与之通信人的资料。
文献[2]给出的签名方程ak=b+ckAmodn,未知向量(a,b,c)是向量(±r,±s,±1)、(±1,±1,±sr)、(±1,±s,±sr)和(±1,±r,±sr)的任何一个排列,分别有24、12、24和24种。文献[2]给出了其中主要的6种基本签名方程和对应消息恢复方程,如表2所示。
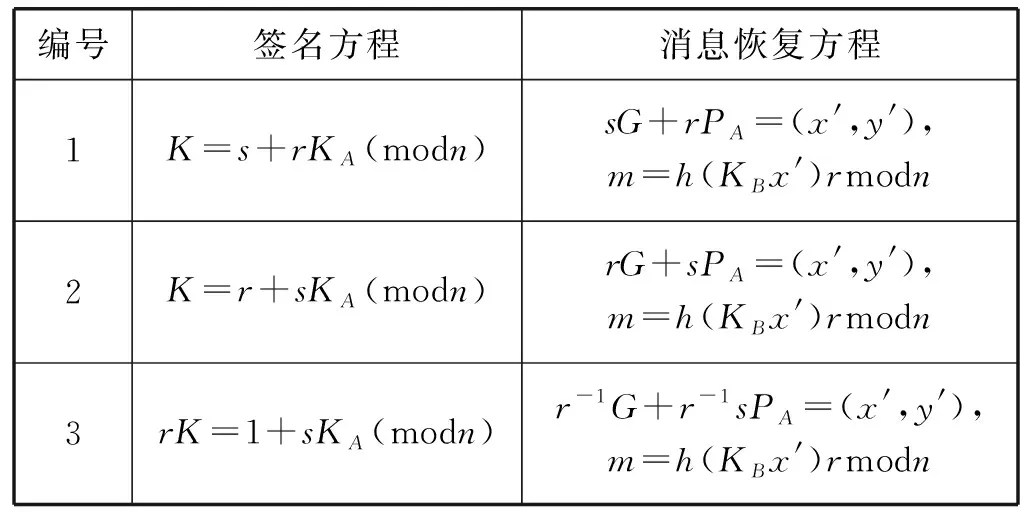
表2 签名方程和消息恢复方程
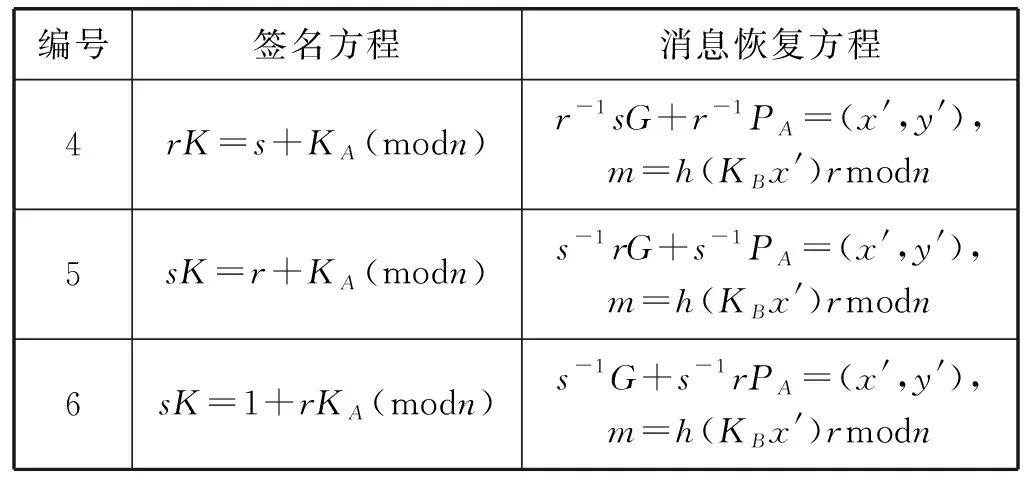
续表2
2.2 改进的基于椭圆曲线的数字签名方案
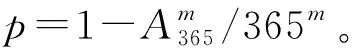
椭圆曲线参数定义如表1所示,以下为改进方案的具体算法:
1) 初始化过程。用户A的两个不同私钥分别为KA1,KA2,其中KA1,KA2∈Zn,KA1≠KA2;用户A的两个对应公钥分别为PA1=KA1G,PA2=KA2G。
用户B的私钥为KB∈Zn,对应的公钥为PB=KBG。
2) 签名的产生过程。
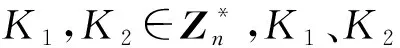
(2)A计算R=(K1+K2)PB=(x,y),r=h(x)-1m(modn)若r=0,则返回(1)。
(3)A再计算s1=K1+rKA1(modn),s2=K2+rKA2(modn),若s1=0或s2=0,则返回(1)。
(4) 以(r,s1,s2)作为A对消息m的签名。
3) 消息确认和签名验证过程。签名(r,s1,s2)被传给B,需要进行验证签名,B获取椭圆曲线的各个参数及A的公钥,并计算:
(1) 进行检验,确定r、s1、s2在 区间[1,n-1]上,如果没有在此区间之上,B可以做出拒绝签名的决定。
(2)B计算X=s1G+s2G-rPA1-rPA2=(x′,y′)和m=h(KBx′)r(modn),KBx′为KBX的横坐标。
(3) 若X=0,那么B有不接受签名的权利。否则,B可以对原始消息进行计算,获取消息末尾数据,并对身份的冗余位进行确认,如果确认无误,B可以接受签名,反之拒绝。
此签名体制是否具有正确性,需要下式来证明:
R=(K1+K2)PB=(K1+K2)KBG=
KB(K1+K2)G=
KB(s1G+s2G-rPA1-rPA2)=
KB(x′,y′)
m=h(KBx′)r(modn)
X=s1G+s2G-rPA1-rPA2=
K1G+rKA1G+K2G+rKA2G-r(KA1+KA2)G=
K1G+K2G=(K1+K2)G=(x′,y′)
类似地,针对表2本文还给出主要的6种改进的算法,签名方程和消息恢复方程如表3所示,其中KBx′为KB(x′,y′)的横坐标。

表3 改进的签名方程和消息恢复方程
2.3 数字签名方案的安全性和复杂度分析
在此仅对第一种方案进行分析,其他6种算法类似,具体分析如下:
1) 若攻击者想对改进的签名方案攻击,利用Fq上求解方程dG=Q(modq)或d=logGQ(modq)。与有限域上的DLP相比,ECDLP的难度更大。在目前所采用的方法中,目前有两种方法能够达到较为理想的效果,一种方法是Pohlig-Hellman方法,另一种方法是Pollard-ρ方法。需要探讨两类特殊的椭圆曲线,可利用有效的方法:(1) 运用概率亚指数算法,选取超奇异椭圆曲线,由于其具有特殊性,采用Mov算法以及FR算法,那么能够予以解决ECDLP的问题;(2) 可以选取异常椭圆曲线,需要运用SSSA算法,那么能够解决ECDLP的问题。
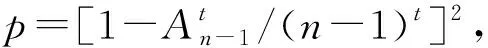
3) 攻击者为了达到目的而企图冒充A,对消息m行使签名权,在实际操作时,要随机选取K1、K2计算R=(K1+K2)PB=(xR,yR),r=h(xR)-1m(modn),s1=K1+rKA1,s2=K2+rKA2,这需要解决椭圆曲线离散对数问题(ECDLP问题)由此可知,攻击者冒充A产生有效签名是不可行的。
4) 改进方案与原方案的复杂度进行比较,改进方案初始化过程和签名过程中遵循两个密钥的思想,改进方案需要增加两次椭圆曲线标量乘运算和一次模运算,与椭圆曲线倍点乘运算比较,大整数模运算可以忽略,运算量增加不大,但是改进方案提高了安全性能。
3 MATLAB实例分析
实例如果签名人C要对摘要N=1 234进行签名,设N的前三位所代表的是消息,最后一位是消息冗余位。系统所选定的椭圆曲线为v2=u3+3u+45(mod 8 831)(如图1所示),基点Q=(4,11),其阶p=4 427。
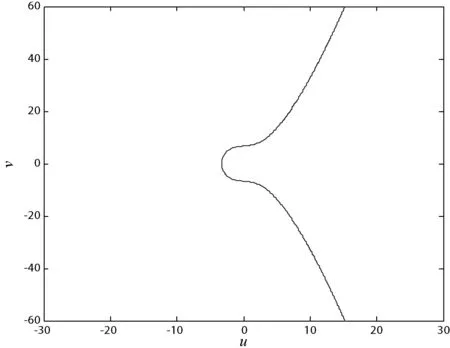
图1 椭圆曲线:v2=u3+3u+45
对数字签名算法进行实例分析,根据已知条件,计算如下:
1) 系统的初始化。签名人C的私钥为:KC1=113,KC2=225。
签名人C对应的公钥分别为:
PC1=KC1Q=(5 908,4 180)
PC2=KC2Q=(1 086,7 000)
验证签名人D的私钥为:KD=221。
验证签名人D的公钥为:
PD=KDQ=(3 829,4 859)。
2) 签名人C对消息摘要N产生签名过程。
(1) 签名人C选择两个随机数,分别为:t1=152,t2=284,然后计算M′=t1Q+t2Q=(459,7 517)。
(2) 签名人C计算:
M=(t1PD+t2PD)=(974,7 560)=(u,v)
e=H(u)-1N(mod4 427)=
H(974)-1×1 234=1 383
(3) 签名人C接着计算:
sig1=t1+eKC1(mod 4 427)=1 486
sig2=t2+eKC2(mod 4 427)=1 569
(4) 可得到签名人C对消息摘要N的签名为(e,sig1,sig2)=(1 383,1 486,1 569),然后签名人C将签名(e,sig1,sig2)=(1 383,1 486,1 569)发送给验证人D。
3)D作为签名验证人,对消息摘要N的恢复和验证。首先,D收到签名(e,sig1,sig2)=(1 383,1 486,1 569),需要进行下载操作,获取域参数和C的公钥,并进行如下计算:
(1) 签名人D首先对签名进行检验,验证(e,sig1,sig2)=(1 383,1 486,1 569) 的每个分量值是否在区间[1,4 426]上。若否,则该签名无效;若是,则进行步骤(2)的运算。
(2) 签名人D接着计算U=sig1Q+sig2Q-ePC1-ePC2=(u′,v′)=(8 811,6 607)和N=H(KDu′)e(mod 4 427)=1 234。其中KDu′为KDU的横向坐标值。
(3) 签名人D经过计算可得,原始消息摘要N=1 234,并检验消息N的最后一位冗余位值为4。结果正确,所以签名人D验证签名有效。
4 结 语
本文对已有文献的数字签名方案的安全性和复杂度进行分析,提出改进的基于椭圆曲线的数字签名方案,
该方案可以有效抵抗生日攻击,并对方案进行安全性分析和运算量分析,最后通过MATLAB实例进行仿真验证,改进方案运算量低,并易于实现。
