基于数据分类的循环不变式自动生成
2023-02-17王承毅
路 红 王承毅 黄 皓
1(南京理工大学紫金学院 江苏 南京 210003) 2(南京大学计算机科学与技术系 江苏 南京 210023)
0 引 言
软件作为当今信息化社会的重要基础设施,已广泛应用于能源、交通、通信、金融和国防等安全攸关领域中[1]。然而,随着软件集成程度的提高和软件系统结构的日益复杂,各类软件的高可信性越来越不能保证。软件验证以逻辑和数学为基础,支持软件进行严格的形式化规约和验证,是确保软件可信性的一种有效措施[2-3]。软件验证的目标是证明程序在任何执行路径下均满足一定的形式化规约,即程序在确定的条件下执行结束后便可满足一定的要求。软件验证的一般步骤是针对待验证的程序撰写形式化规约(如前置条件、后置条件和循环不变式),然后利用自动验证工具或交互式定理证明器验证给定程序是否满足所撰写的形式化规约[4-5]。为了提高验证效率、简化验证难度,出现了Z3[6]、Danfy[7]和Why3[8]等自动化验证工具。运用这类自动化验证工具对代码量较少的程序进行验证,无须验证者撰写大量证明脚本,仅须按照自动化验证工具的规范撰写待验证程序的形式化规约,即可快速得到程序是否正确的验证结果。然而,为程序提供合适的形式化规约,尤其是循环不变式,需要验证者依据对程序的正确理解进行手工撰写,这对于程序验证者来说是一项任务繁重的工作且容易出现错误。因此,研究循环不变式的自动生成方法,减少人工撰写程序形式化规约的工作量以及因人工撰写形式化规约导致的验证错误问题,已成为软件验证研究领域关注的一个重要问题[9]。
1 相关工作及贡献
近年来,已有一些研究致力于循环不变式的自动生成方法研究。文献[10-12]运用参数模板将循环不变式设置为一个参数模板,然后利用前置条件和后置条件进行约束求解。文献[13-17]利用抽象解释方法构造多项式循环不变式,在语义等式基础上进行多次不动点迭代计算,从而生成循环不变式。这些构造循环不变式的方法均受限于所设定的模板。文献[18]使用了“GUSESS AND CHECK”方法,将生成循环不变式的过程分为GUSESS和CHECK两个阶段。其中,GUSESS阶段主要生成候选不变式,CHECK阶段主要验证GUSESS阶段所生成的候选不变式是否正确。若不正确则继续迭代执行GUSESS和CHECK两个阶段的步骤,直到生成一个正确的循环不变式为止。文献[19]运用游戏和众包策略将生成候选不变式的过程交给网络游戏玩家来完成。文献[20]提出了一种基于数据分类生成候选不变式的方法,但不支持具有分支条件的循环语句生成循环不变式。文献[21]提出的不变式生成方法虽然解决了具有分支条件的循环语句的循环不变式生成问题,但研究的是针对抽象程序进行不变式的生成方法。
本文提出了一种基于数据分类的方法实现面向可运行的C程序自动生成循环不变式。本文的主要贡献在于:
(1) 设计了一种自动生成可执行C程序后置条件的算法,并构造相应的Hoare三元组,作为自动生成候选循环不变式的输入。
(2) 所提出的基于KSVM的自动循环不变式生成方法,支持生成包含析取和合取这两种谓词逻辑关系的、多项式不等式形式的循环不变式。
(3) 对于分支循环程序,首先通过路径敏感分析将其划分成多条执行路径,然后针对每条执行路径分别使用KSVM分别生成候选不变式,最后使用SMT求解器检查其正确性,从而得到具有分支条件的循环程序的循环不变式。
(4) 所提出的方法在31个基准测试程序上进行评估和比较。实验结果表明,本文所提出的方法能够为最多的循环程序生成有效的循环不变式。
2 问题定义与方法概览
2.1 问题定义
为了清晰阐述本文所需解决的问题,我们对本文中所使用的符号进行界定。符号C表示循环条件,符号B表示循环体,符号V={v1,v2,…,vn}表示与循环语句相关的变量集合。符号Bodyi(v)={v1→xi,v2→yi,…,vn→mi}表示循环程序执行第i次循环后V中各个变量的值。符号P表示循环语句的前置条件,即在执行某条程序语句前所需要满足的公式集合。符号Q表示循环语句的后置条件,即在执行某条语句后应该要满足的公式集合。
Loop_A和Loop_B是两个可运行的C循环程序。其中,Loop_A的变量集合V={i,j,n},第2行的assume语句表示前置条件P,第7行的assert语句表示后置条件Q。Loop_B的变量集合V={x,y},第2行的assume语句表示前置条件P,第8行的assert语句表示后置条件Q。
算法1循环程序Loop_A
1: int loop_function (int i, int n){
2: assume(i==0&&j==0);
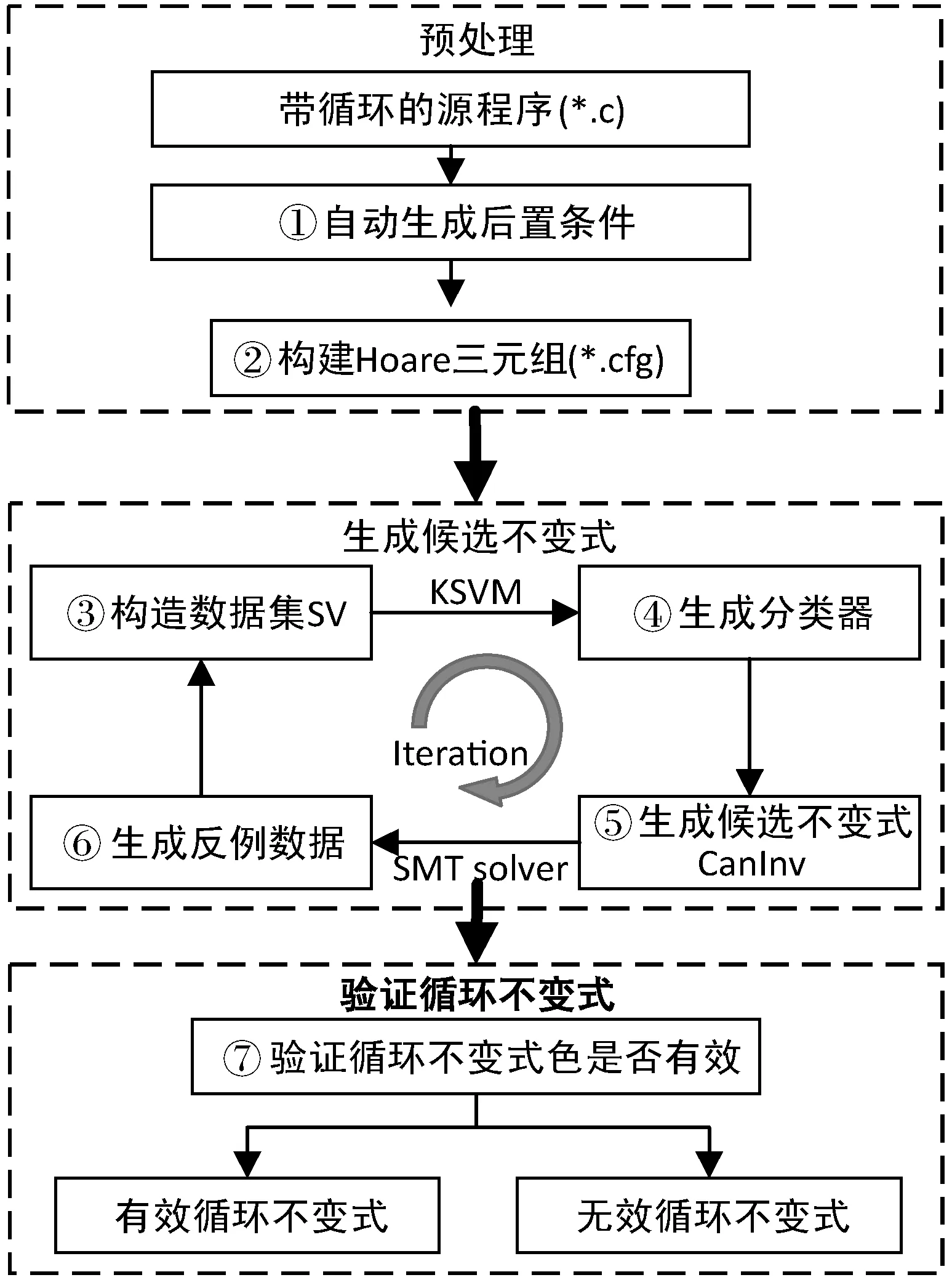
3: while (i 4: i=i+1; 5: j=j+1; 6: } 7: assert(i==n-1&&j==i); 8: return j; 9: } 算法2循环程序Loop_B 1: int loop_function (int x, int y) { 2: assume(x>0||y>0); 3: while (x+y<-2) { 4: if (x>0) 5: x=x+1; 6: else 7: y=y+1; 8: } 9: assert(x>=0||y>=0); 10: return x+y; 11: } Hoare逻辑为程序验证提供了一套公理和规则[22]。在文献[23]中,基于Hoare逻辑的循环语句验证使用一种断言来验证程序所满足的性质,该断言即为循环不变式。 定义1断言I是循环语句的循环不变式,当且仅当其满足以下3个条件: (1)P→I。 (2)I∧C→Bodyi(v)∧I。 (3)I∧C→Q。 条件(1)表示循环语句的前置条件P可推导出断言I,即断言I在循环的入口点是成立的。条件(2)表示断言I在循环体执行前后均成立,即在循环体执行之前的程序点、循环体执行之后的程序点及循环语句的退出点均成立。条件(3)表示断言I和循环语句的退出条件可推导出后置条件Q,即断言I可用于后置条件的正确性验证。条件(1)和条件(2)成立可保证断言I是循环语句的循环不变式,条件(3)说明循环不变式I可证明循环语句执行结束之后应满足的性质。 从定义1可以看出,如果一个循环不变式I成立,则循环程序执行前变量集合的取值V0和任意一次循环执行后变量集合的取值Vi均使得I成立。否则,循环不变式I不成立。从另一个角度来看,假如已知数据集SV+使条件(1)、(2)、(3)均成立,而数据集SV-使条件(1)、(2)、(3)中的任意一个均不成立,那么循环不变式I将是SV+和SV-的分类器。基于上述发现,本文使用核支持向量机(Kernel Support Vector Machines,KSVM)[24]求解该分类器,进而得到相应的循环不变式。 使用KSVM作为一种分类器来自动生成循环不变式的过程如图1所示,整个过程共分为三个阶段。第一个阶段是预处理,目标是实现对程序中循环语句后置条件的自动生成,并将前置条件、循环语句和后置条件组成Hoare三元组(文件命名为*.cfg)。第二个阶段是迭代生成候选不变式。首先,依据循环语句的前置条件随机生成测试数据,以这些测试数据作为循环变量的初始值运行循环语句,并收集循环语句执行过程中循环变量的值,组成样本数据集SV。对数据集SV,依据所生成的Hoare三元组判定SV中的每一个样本数据s是否属于循环不变式的范围进行标注,然后使用KSVM对标注后的数据集SV进行分类,从而自动生成候选不变式。为了减少迭代次数,在候选不变式的边界线上选择有限个样本数据加入到SV中,训练用于生成候选不变式的KSVM分类器,直到其不再发生变化为止。最后,运用SMT求解器验证候选不变式是否存在不满足Hoare逻辑的反例数据。若存在反例数据,则将其加入到SV继续进行下一次迭代,直到产生一个循环不变式为止。其中,数据集SV的收集有两种方法:一种是依据每个变量的定义域随机生成有限组变量的值。另一种是利用SMT求解器分别生成满足前置条件P和不满足前置条件P的变量值。第三个阶段是验证自动生成的候选循环不变式是否符合条件(1)、(2)和(3)中,输出结果为有效循环不变式或无效循环不变式。 图1 基于数据分类的循环不变式自动生成过程 根据定义1,循环不变式与前置条件P、循环条件C、循环体B和循环语句的后置条件Q相关。后置条件Q是生成循环不变式的关键,本节将重点阐述后置条件Q的自动生成算法。文献[25]依据循环条件C的特点,将循环语句的类型分成IVCondition和NIVCondition两种。如果循环条件C所包含的每个循环控制变量都是可归纳的,则该条件属于IVCondition类循环条件。否则,该条件属于NIVCondition。本文所提出的自动后置条件生成算法是面向具有IVCondition类循环条件的循环程序。 算法3描述的是循环语句后置条件的生成方法。第1步,依据循环的前置条件P、循环条件C和循环体B中所出现的变量构造变量集合V。第2步,计算循环体B执行一次循环后,变量集合V中各个变量的增量Δ(V)。假设程序执行第i次循环后V的值为Vi,程序执行第i+1次循环后V的值为Vi+1,则Δ(V)=Vi+1-Vi。第3步,使用边界值分析法计算循环执行次数k。假定给定的循环语句在开始执行前循环变量的值满足前置条件P和循环条件C,当执行k次后程序终止,则表示该循环体B在执行k次之后循环变量的值不满足循环条件C。因此,在循环语句执行k-1次后,V的值Vk-1满足循环条件C,在执行k次循环后,V的值Vk不满足的循环条件,根据这两个条件可计算出循环体B的执行次数k。第4步,依据第2步和第3步计算的结果生成关于集合V中每个变量在循环体B执行结束时的不等式表示形式。最后,对第4步得到的各个变量的值的表示形式进行简化,即可得到后置条件Q。 算法3循环语句后置条件的自动生成算法 输入 前置条件P,循环体B。 输出 后置条件Q。 1.依据前置条件P,循环条件C和循环体B构造变量集合V; 2.根据循环体B执行第i次循环和第i+1次循环后的V值的变化,计算循环增量Δ(V); 3.使用边界值分析法计算循环的迭代次数k; 4.依据Δ(V)和k,对变量集合V中的每个变量计算循环执行结束时的值(不等式形式的表示); 5.依据前置条件P对第4步的不等式进行简化并输出后置条件Q。 就循环程序Loop_A来说,其后置条件的自动生成步骤如下:首先,依据其前置条件P、循环条件C和循环体B所影响的变量,构造变量集合V={i,j}。循环体B执行1次后,变量i和j的增量分别为Δ(i)=1和Δ(j)=1;循环体B执行k-1次后,变量的值分别为ik-1=i+k-1和jk-1=j+k-1;循环语句执行k次后,变量的值分别为ik=i+k和jk=j+k。循环体B执行k-1次后变量ik-1满足循环条件i 在现阶段的初中语文课外阅读教学中,为使教师的教学方法真正被学生接受和理解,教师可以采用阶梯式阅读教学方法,根据学生的学习情况和理解能力选取合适的读本,逐步实现课外阅读教学目标。学生在阶梯式课外阅读教学中,阅读难度逐渐增强,给学生阅读水平提供循序渐进的过程,有利于学生阅读能力的发展和提高,是教师课外阅读教学的有效方法。 循环程序Loop_B后置条件的自动生成步骤如下:首先,依据前置条件P、循环条件C和循环体Q的变量,得到其变量集合V={x,y}。该程序的循环体有两种执行路径,分别标记为pathi和pathj,pathi的循环条件为x+y<-2∧x>0,在该执行路径下执行1次循环后变量x的增量为Δ(x)=1,执行k次和k-1次后变量x的值分别为xk-1=x+k-1和xk=x+k。依据该执行路径的循环条件,简化后可得k=-2-x-y。那么,xk=-y-2。最后,再利用前置条件P和Z3简化,可得到该执行路径的后置条件Qi=(x>0)。同理,得到另外一种执行路径的后置条件Qj=y>0。整个循环程序Loop_B的后置条件Q为x>0‖y>0。 Hoare三元组描述一段代码在执行后如何改变程序的状态,其由前置条件P,后置条件Q和程序组成。在生成循环的后置条件Q之后,循环语句的Hoare三元组可快速构造出。Loop_A和Loop_B的Hoare三元组如图2所示。在图2中,第1行表示循环语句的变量集合V,第2行表示循环执行前变量的初值,第3行表示循环的前置条件P,第4行表示循环条件C,第5行表示循环体B,第6行表示后置条件Q。 图2 循环语句的Hoare三元组 算法4是提出的基于数据分类的循环不变式自动生成方法。算法4以第3节所生成的Hoare三元组作为输入,执行后输出所得到的循环不变式I。 算法4循环不变式的自动生成算法 输入 Hoare三元组,time_limit=600 s。 输出 循环不变式I。 1. 依据前置条件P随机生成测试数据,得到数据集SV; //当前时间 3.Whiletime_limit>=0do{ 4. 以数据集SV作为测试数据,运行循环语句并记录循环变量值,将其加入到数据集SV; 5. 标注数据集SV的变量值是否属于循环不变式的范围,将其分为CE(SV)、PE(SV)、NE(SV)和NP(SV)四类样本; 6. 使用KSVM方法对SV中的样本进行分类,生成候选不变式CanInvr; 7. 验证CanInvr是否能够存在反例使得条件(1)、(2)、(3)的取反成立,如果成立则将反例加入到数据集SV,继续迭代下一次循环,如果不存在反例,则I=CanInvr; 8. time_limit=current_time-start_time;} 9. 验证循环不变式I是否有效。 构造合理的数据集是运用KSVM生成循环不变式的基础。假设数据集为SV,且其应包含满足循环不变式的数据集SV+和不满足循环不变式的数据集SV-。算法4中的第1行主要是构造循环执行之前变量的初始值。首先,通过随机方式生成满足前置条件的数据集SP和不满足前置条件的数据集SN,这两种方式构造测试数据集SV=SP∪SN。其次,以测试数据集SV作为循环体执行的初始值,依据循环条件执行有限次循环语句,并记录每一次循环结束后循环变量的值,组成数据集SC,并将数据集SC加入到数据集SV中,即SV=SP∪SN∪SC(见算法4的第4行)。第三,依据文献[21]提出划分数据集SV中的一个数据s是否满足循环不变式的方法,将SV划分为CE(SV)、PE(SV)、NE(SV)和NP(SV)四种分类集(见算法4的第5行)。 CE(SV)={s∈SV}|∃s0,s′,s0∈P∧s0→ s→s′∧s′∈C∧s′∈Q (1) CE(SV)包含数据集SV中不能通过Hoare逻辑验证程序的数据。式(1)表示数据集SV中一个数据样本s属于集合CE(SV)的条件为:存在数据s0和s′,s0满足循环前置条件P,执行一次或多次循环体B后经过中间某个状态s得到s′,但数据s′不满足后置条件Q。如果集合CE(SV)非空,则表示Hoare三元组不能被验证。 PE(SV)={s∈SV}|∃s0,s∧′,s_0∈P∧s_0→ s→s′∧s′∈C∧s′∈Q (2) PE(SV)包含数据集SV中属于数据集SV+的样本数据,其一定满足循环不变式。式(2)表示数据集SV中的数据样本s属于集合PE(SV)的条件为:存在数据s0和s′,s0满足循环前置条件P,执行一次或多次循环体语句B后得到s′,当循环结束时s′满足后置条件Q。 NE(SV)={s∈SV}|s0,s′,s0∈P∧s0→ s→s′∧s′∈C∧s′∈Q (3) NE(SV)包含数据集SV中属于数据集SV-的样本数据,其一定不满足循环不变式。式(3)表示表示数据集SV中的一个数据样本s属于NE(SV)的条件为:存在数据点s0和s′,s0不满足循环前置条件P时,执行一次或多次循环体语句B后经过中间数据s得到s′,循环终止时s′不满足后置条件Q。 NP(SV)=SV-CE(SV)-PE(SV)-NE(SV) (4) 式中:NP(SV)表示SV中存在的、不能确定属于上述三类样本的数据集合。 以循环程序Loop_A为例,假设为变量集合(i,j,n)随机生成满足前置条件和不满足前置条件的数据集为(0,0,29)、(1,7,7)和(0,0,-8),以这3组数据作为初始变量值,执行循环体后可得到变量的中间状态值分别为<(0,0,29),(1,1,29),(2,2,29),…,(30,30,29)>、<(1,7,7)>和<(0,0,-8)>。然后,依据CE、PE、NE和NP的定义,对这些对数据进行标注,CE(SV)为空,PE(SV)为<(0,0,29),(1,1,29),(2,2,29),…,(30,30,29)>,NE(SV)为<(1,7,7)>和NP(SV)为<(0,0,-8)>。 通过上述方法生成数据集SV并对其所属类别进行标注。根据算法4中第6行,采用KSVM方法对数据集SV进行分类,可得到一个候选不变式CanInv,具体生成步骤如下: (1) 利用KSVM对数据集SV进行分类,生成一个分类器,将它作为初始候选不变式CanInv; (2) 在分类器边界上选取样本添加到SV中,通过多次迭代得到优化后的候选不变式CanInv。 通过步骤(1),基于随机生成的测试数据,采用KSVM生成一个线性不等式,即第一个候选不变式。该候选不变式是由有限个随机样本分类得到,其不能保证对所有可能的测试数据都能准确分类。因此,得到一个初始候选不变式CanInv后,通过步骤(2),在候选不变式的分类边界上选择两个样本数据,将这两个样本数据加入到SV中后,再次使用KSVM生成新的候选不变式CanInv。当在候选不变式的分类边界上选择的数据样本不能生成新的候选不变式CanInv时,生成候选不变式的过程便可结束,从而得到优化后的候选不变式。选择样本的过程是先将得到的候选不变式转换为等式,然后假定其中某一个变量为任意整数,求其他变量的值。例如,Loop_A的初始候选不变式为342-7×i+8×n≥0,其分边界为等式342-7×i+8×n=0。假定n=1,从而求得i=60,得到变量集合(n,i)的一个选择样本数据为(1,60)。 此外,为了生成合取式的循环不变式,每次在集合NE(SV)中选择一个数据样本s,使用KSVM将数据s和集合PE(SV)中的数据进行分类得到一个分类器,迭代有限次这个过程后,直到NE(SV)为空,最后将每个分类器按照合取式关系生成候选不变式CanInv[22]。例如,采用这种方法,可生成Loop_A的候选循环不变式(78-n≥0)∧(1-i+j≥0)∧(47-i≥0)∧(i-j≥0)。 对于带分支条件的循环,为其生成循环不变式的基本方法是:首先,按照路径分析方法将循环分成多条执行路径;然后,对每条路径按照上述步骤(1)和(2)中的方法,使用KSVM的方法生成候选不变式;最后,将针对不同执行路径求得的循环不变式进行综合,从而得到各个循环不变式的析取式,即可分支循环程序的候选循环不变式。例如,Loop_B的循环体有两个执行路径:pathi为(4,6,7)行,pathj为(4,8,9)行。pathi的候选循环不变式为x>0,pathj的候选循环不变式为y>0,则分支循环程序Loop_B的候选循环不变式为x>0‖y>0。 有效的循环不变式必须是能够依据Hoare逻辑规则验证循环。而4.1节得到的候选不变式是通过KSVM分类测试样本数据得到的不变式,不能确定其是否为有效循环不变式,故本节目标是验证候选不变式的有效性,进而求得可验证的循环不变式。 P∧CanInvr (5) (SV(sv+)∧C,Body)∧CanInvr (6) CanInvr∧Q∧C (7) 式(5)-式(7)分别是Hoare逻辑规则中循环不变式的取反,即CanInvr。如果一个候选循环不变式是有效的循环不变式的话,其必定不会使得式(5)-式(7)中任何一个条件成立。算法4中的第7行,则是通过SMT求解器(如Z3)验证候选不变式是否满足式(5)-式(7)中的任意一个,如果满足,将会产生一个反例数据,将该反例数据加入到数据集SV中,迭代调用KSVM算法训练分类器,直到没有反例为止。如果不满足式(5)-式(7),则候选不变式为有效的循环不变式。 使用Z3验证Loop_A的候选不变式是否满足式(5)-式(7)时,得到一组反例(0,0,-31)和(0,0,79),依次将两个数据加入到SV后训练分类器,得到优化的循环不变式为i-j≥0。经Z3验证,i-j≥0为Loop_A的一个有效循环不变式。 为评估本文所提出的循环不变式自动生成方法,使用C++、KLEE[26]和Z3实现了一个原型系统。首先,使用C++实现了后置条件的自动生成。然后,使用约束求解器Z3简化后置条件。其次,将自动生成的后置条件、前置条件以及循环语句构造成Hoare三元组作为输入,随机生成测试数据集并利用Z3生成满足前置条件的测试数据,以这些测试数据作为程序变量的初始值,应用KLEE执行循环语句并记录每次循环体执行后变量的值。最后,使用KSVM方法对这些中间数据进行分类得到候选不变式。最后,使用Z3验证所生成的候选循环不变式是否为可验证的循环不变式。 SV-Comp[27]是由慕尼黑大学构建并维护的形式化验证方法的基准测试数据集,为评估形式化验证技术提供了公平的基准测量程序。为验证本文所提出的不变式自动生成方法,我们在SV-Comp2019提供的C测试程序库中选择了被已有的文献[21,28-30]使用的31个测试程序进行实验分析。每个测试程序由前置条件和循环语句组成,所选择的测试程序不包含数组和嵌套循环,且循环条件是可归纳的。为了评估本文所提出算法的有效性,将本文所提出的循环不变式自动生成方法与ZILU[21]、CPAChecker[28]、BLAST[29]和InvGen[30]这四种方法进行对比,实验结果如表1所示。ZILU是一个采用数据分类生成循环不变式的工具,其以循环程序的Hoare三元组开始,运用SVM生成循环不变式。CPAChecker是一款基于抽象解释的循环不变式的自动生成工具。BLAST是一款验证C程序是否满足指定安全属性的自动验证工具,其基于反例自动构造循环不变式。InvGen是一种结合静态分析和动态分析方法自动生成线性算术循环不变式的工具。 表1 基于KSVM生成循环不变式的实验结果 续表1 在表1中,T表示可生成有效的循环不变式,F表示不能生成有效的循环不变式。第1列表示测试用的C程序标识号,第2列是生成循环不变式所需要的样本数据的个数,第3列表示生成循环不变式所需要的平均迭代次数,第4列表示使用本文所提出的方法是否能够生成可验证的循环不变式,后面4列是利用其他4种循环不变式生成方法可否为相应的测试程序生成可验证的循环不变式。 从表1可以看出,ZILU仅可成功为26个测试程序生成可验证的循环不变式。CAPchecker、BLAST和InvGen分别可为28个测试程序生成可验证的循环不变式。相比之下,本文提出的循环不变式自动生成方法可为所有31个测试程序生成候选不变式,仅有两个候选不变式不能验证通过,分别是lh8和lh23。同时,所生成的循环不变式中各个元素关系可以是线性的、析取的或合取的。由此可见,本文所提出的循环不变式生成方法可基于后置条件,采用KSVM分类方法自动生成有效的循环不变式。值得注意的是,本文所提出的方法在生成循环不变式的成本较低,生成一个循环不变式需要的平均测试样本数约为46.1,平均循环迭代次数约为3.5。 本文提出了一种基于数据分类的循环不变式自动生成方法,通过随机生成测试数据、在初始候选不变式的分类边界选择测试数据、KSVM分类等方法,可为可行C循环程序自动生成可验证的循环不变式。实验验证与分析表明,本文所提出的循环不变式自动生成方法不仅能够为较少的循环程序生成有效的循环不变式,而且生成成本较低。2.2 方法概览
3 后置条件的自动生成

4 循环不变式的自动生成与验证
4.1 循环不变式的自动生成
4.2 循环不变式的验证
5 实验分析
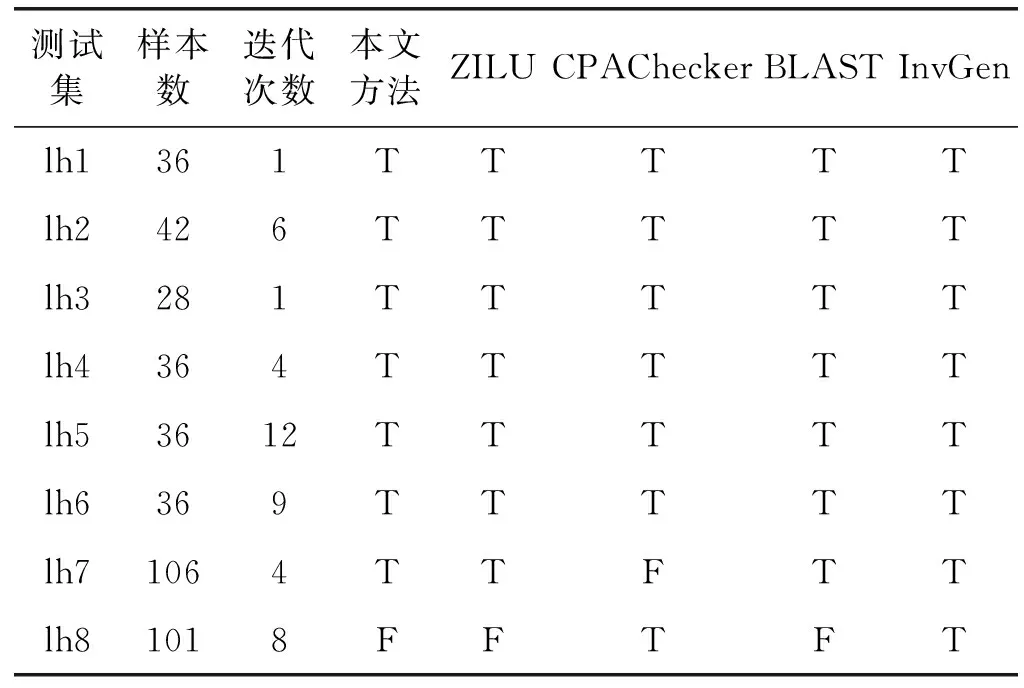
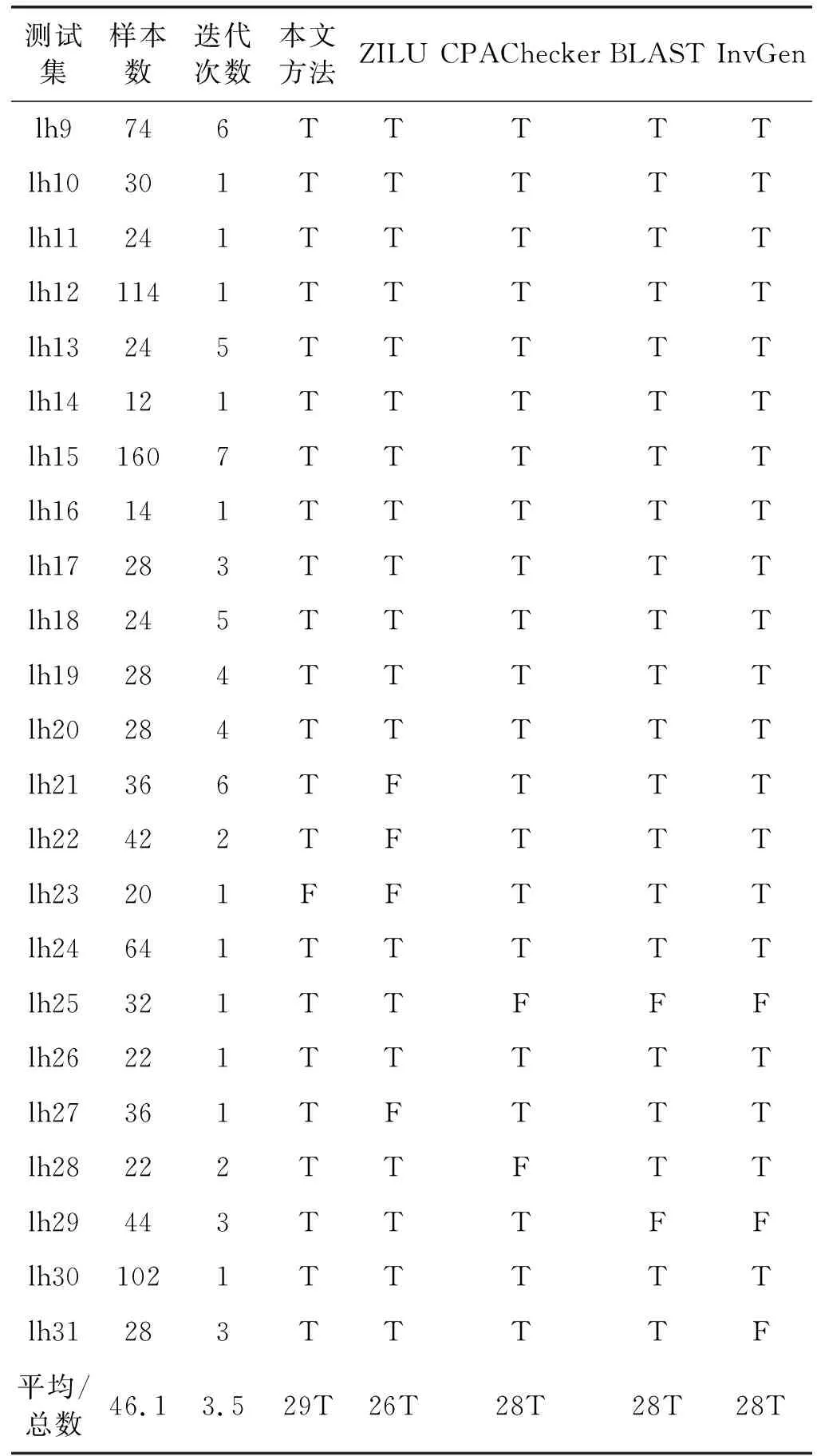
6 结 语
