屏蔽数据下带变点的软件可靠性增长模型
2023-02-17杨剑锋霍雨佳
杨剑锋 霍雨佳 蔡 静
1(贵州理工学院大数据学院 贵州 贵阳 550003) 2(贵州理工学院电气与信息工程学院 贵州 贵阳 550003) 3(贵州民族大学数据科学与信息工程学院 贵州 贵阳 550025)
0 引 言
软件可靠性是软件质量的一个主要属性,在建立软件可靠性增长模型时,通常假设软件的失效过程服从非齐次泊松过程[1-5]。可叠加的NHPP类可靠性模型由一些独立的非齐次泊松过程叠加而成[6-7],它可以用于描述一些基于组件或者对象的大型软件系统的失效过程。叠加模型能够充分地利用组件的失效数据,来评估整个软件系统的可靠性。由于可叠加模型中较多的未知参数,因此如何利用有效的算法求解模型的极大似然估计仍然是值得研究的问题。
屏蔽数据(Masked Data)是指引起系统失效的真实原因不得而知,即导致系统失效原因可能是系统中任意一个组件(对象、子系统、模块)[8]。如今,屏蔽数据下硬件可靠性分析已经取得了许多研究成果[9-13],然而基于屏蔽数据的软件可靠性研究成果较少。由于屏蔽失效数据的存在,导致可叠加模型中有较多的未知参数,因此如何利用有效的算法求解模型的极大似然估计仍然是值得研究的问题。
文献[8]首次使用EM算法解决了可叠加模型中参数的极大似然估计问题,取得了较好的效果。文献[14]利用免疫粒子群算法求解了屏蔽数据下可叠加模型的极大似然估计。然而,这些屏蔽数据下的软件可靠性叠加模型,未考虑软件失效过程中的变点问题。由于受到软件测试过程中各种因素的影响,使得失效过程的统计特性有所变化,例如测试人员的改变等,如今在软件变点可靠性模型上已经取得了一些研究成果[15-18]。
然而,很少有相关文献同时考虑软件的屏蔽失效和失效过程中的变点问题。因此,本文是在同时考虑屏蔽失效数据和多变点的情况下,建立可叠加的软件可靠性增长模型,利用C-Chart方法估计软件失效过程中的变点位置,并给出参数的极大似然估计,利用EM算法对其求解。
1 模型设计
1.1 屏蔽数据
在实际软件开发过程中,由于受软件测试策略及测试费用等问题的影响,使得完整的失效数据很难获得或者需要耗费大量的资源,因此失效数据中出现了屏蔽现象,即导致系统失效的原因不能确定或者某些失效类型不能判断[8]。
对于一个三组间的软件系统,其失效过程特例如图1所示,可以看出,第一个时刻M表示发生失效的原因不知,第二个时刻是组件1导致系统失效。由于失效数据的不完整性,使得软件可靠性模型的参数估计更加复杂。
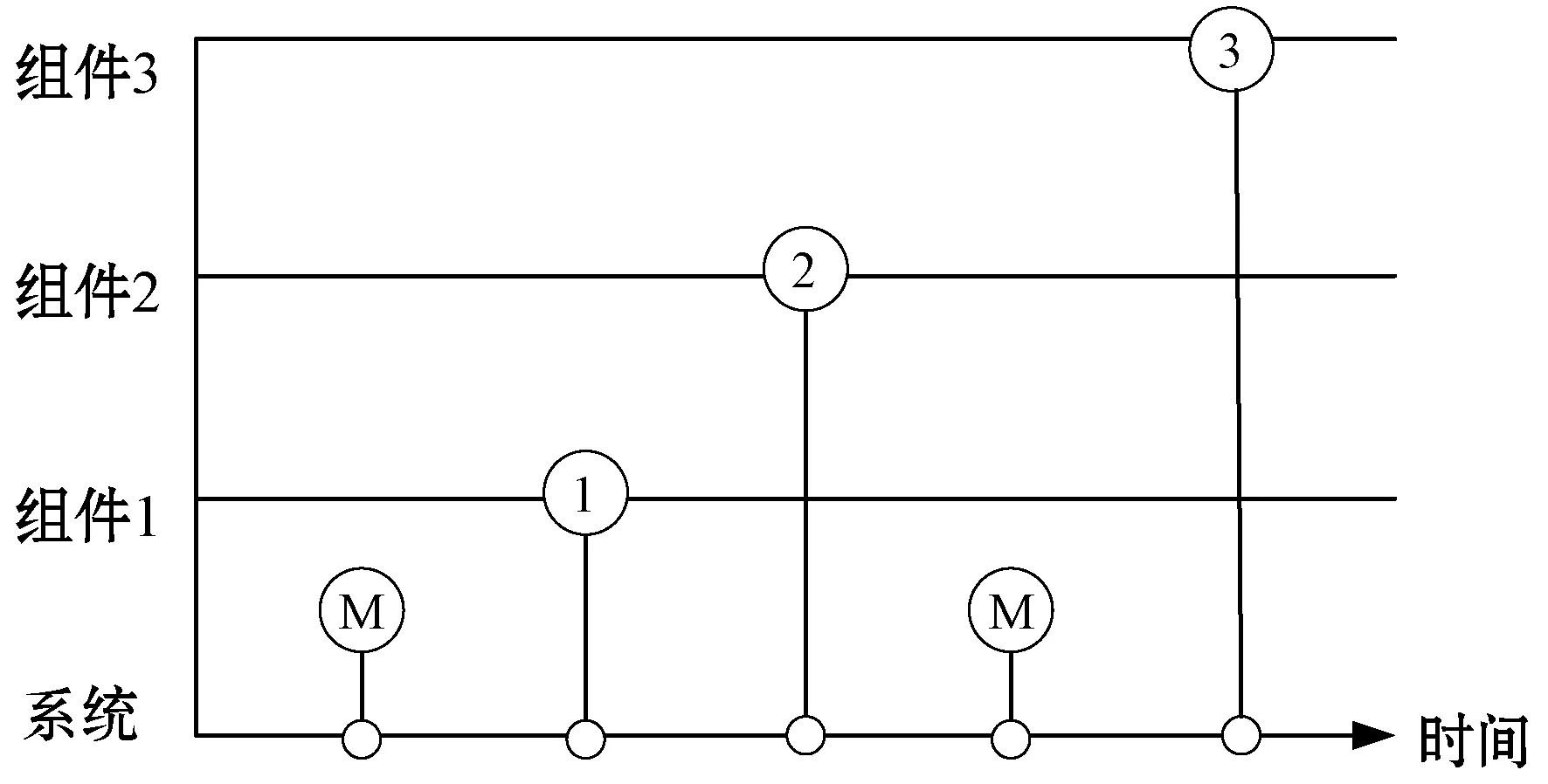
图1 屏蔽数据下软件系统的失效过程
1.2 模型假设
为了建立屏蔽数据下带变点的软件可靠性增长模型,需要如下基本假设:
1) 软件系统中有k个对象(子系统、模块、组件)。
2) 每个组件i的失效过程服从NHPP{Ni(t),t≥0},其均值函数分别为mi(t),i=1,2,…,k。
3) {Ni(t),t≥0},i=1,2,…,k相互独立。
4) 软件系统的累计失效数为N(t),由下式计算:
(1)
因此,软件系统的均值函数为:
(2)
进一步可得软件系统的失效强度函数为:
(3)
根据模型的基本假设和非齐次泊松过程的性质,可得软件系统的可靠性函数为:
R(t)=P{N(t)-N(0)=0}=
exp{-[m(t)-m(0)]}=
(4)
另外,软件系统在(t,t+Δt)时间区间里不发生失效的概率为:
R(Δt|t)=exp{-[m(t+Δt)-m(t)]}
(5)
1.3 模型建立
1.3.1屏蔽数据下带变点的可靠性模型一般性框架
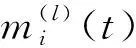
(6)
从而可得软件的失效强度函数为:
(7)
1.3.2屏蔽数据下带变点的G-O可靠性模型
可叠加的G-O模型[19]由Ohba提出[20],该模型的均值函数为每个组件均值函数的和,具体如下:
(8)
式中:k为系统组件(子系统)的个数;ai、ri分别是组件i的故障数和故障检测率。由式(6)和式(8)可得G-O模型下软件系统的均值函数m(t)为:
(9)
式中:ali和rli分别是组件i在第l个变点区间上的初始故障数和故障检测率。
由式(7)和式(9)可得G-O模型下软件的失效强度函数为:
(10)
2 参数估计与模型评估准则
本文采用C-Chart技术估计软件失效过程中的变点位置,使用EM算法解决似然函数的最大化问题。
2.1 基于C-Chart的变点估计

(11)
(12)
(13)
式中:fi为第i个观测区间上的故障数。假定有连续至少8个观测值位于中心线的同一侧,可能会有一个变点产生[15]。因此,通过C-Chart方法可以估计变点的位置。
2.2 模型参数的极大似然估计
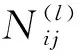
观测到的系统屏蔽失效数据可以表示为:
(14)
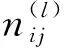
易知,在时间区间[tj-1,tj]⊆(τl-1,τl]上观测值成功发生的事件为:
(15)
其中:
(16)

(17)
式中:
(18)
(19)
(20)
(21)
将式(18)和式(20)代入式(17)得:
(22)
因此,可得似然函数如下:
(23)
可以在不同的变点区间上分别求似然函数的最大值,从而得到参数的极大似然估计。但是,从似然函数公式可以看出,屏蔽数据下参数的似然函数非常复杂,通过数值算法也是很难求出极大似然估计。本文将采用EM算法解决极大似然估计的问题。下面分别讨论完全屏蔽失效和无屏蔽失效两种特殊情况下的似然函数。
1) 完全屏蔽失效情形。
(24)
2) 无屏蔽失效情形。
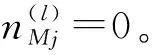
(25)
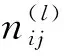
(26)
此种情形下,我们只需要在不同的变点区间(τl-1,τl]和不同的组件i(i=1,2,…,k)下分别求对数似然函数的最大值即可。
2.3 模型评估准则
均方误差(MSE)是一种常见的模型评估准则,由于本文考虑带变点的屏蔽失效问题,因此模型的MSE定义为:
(27)
3 极大似然估计的EM算法
当屏蔽数据存在时,系统的失效数据包含可观测的数据xobs和缺失的数据xmiss两个部分,可以采用EM算法解决似然函数过于复杂的关键性问题,EM算法的过程如下:
E步骤:对于未知参数向量θ当前的估计值θ(s),计算对数似然函数的条件期望:
Q(θ(s),θ)=Eθ(s){log(θ|xobs,xmiss)|xobs}
(28)
M步骤:通过计算Q(θ(s),θ)的最大值,找到参数θ的新估计θ(s+1)。
一般情况下,序列{θ(s),l=1,2,…}将收敛于参数的极大似然估计值[13,14]。假设在失效过程中用C-Chart方法估计到了L个变点,在每个区间(τl-1,τl]上用EM算法求解参数的极大似然估计。下面将描述在区间(τl-1,τl]上的EM算法步骤,其他变点区间可以类似计算。
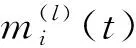
Q((θ(l))(s),θ(l))=
(29)
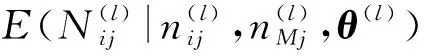
Qi((θ(l))(s),θ(l))=
(30)
i=1,2,…,k
(31)
下面给出在某个变点区间(τl-1,τl]上使用EM算法估计参数的步骤:

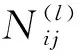
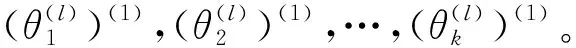
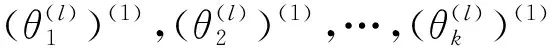
步骤5重复步骤2至步骤4,直到满足条件为止。
因此,根据上面的EM算法步骤,可以求出所有变点区间(τl-1,τl],l=1,2,…,L+1上的参数估计值θ(l)。
4 案例分析
4.1 故障数据
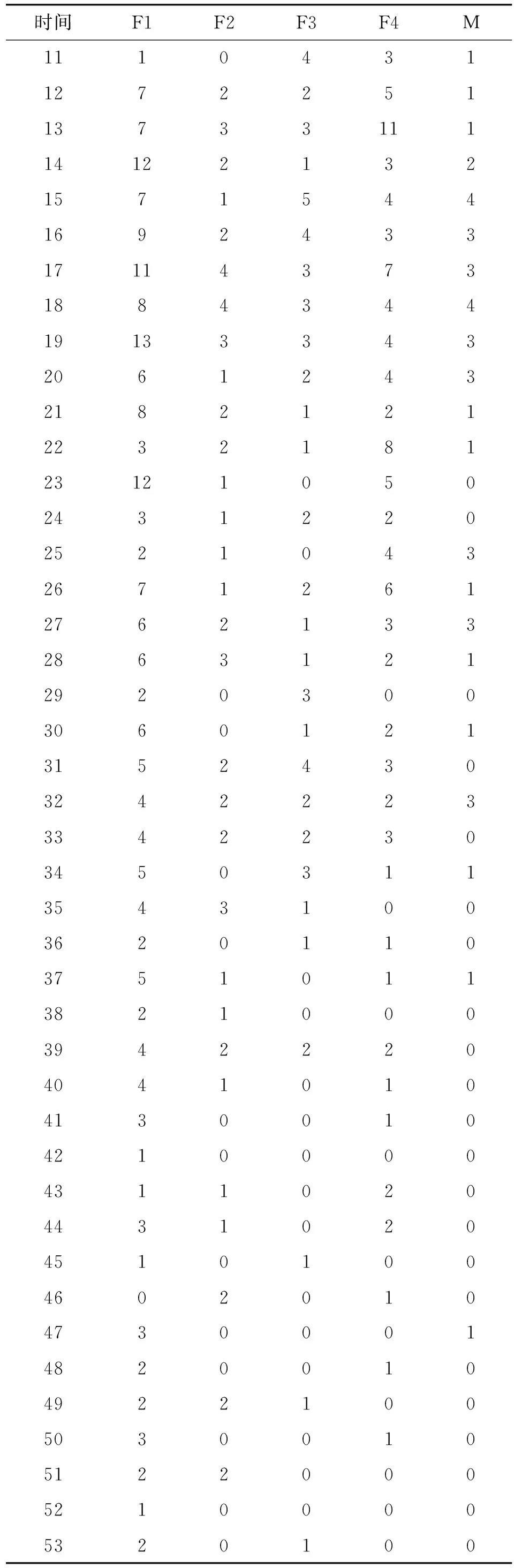
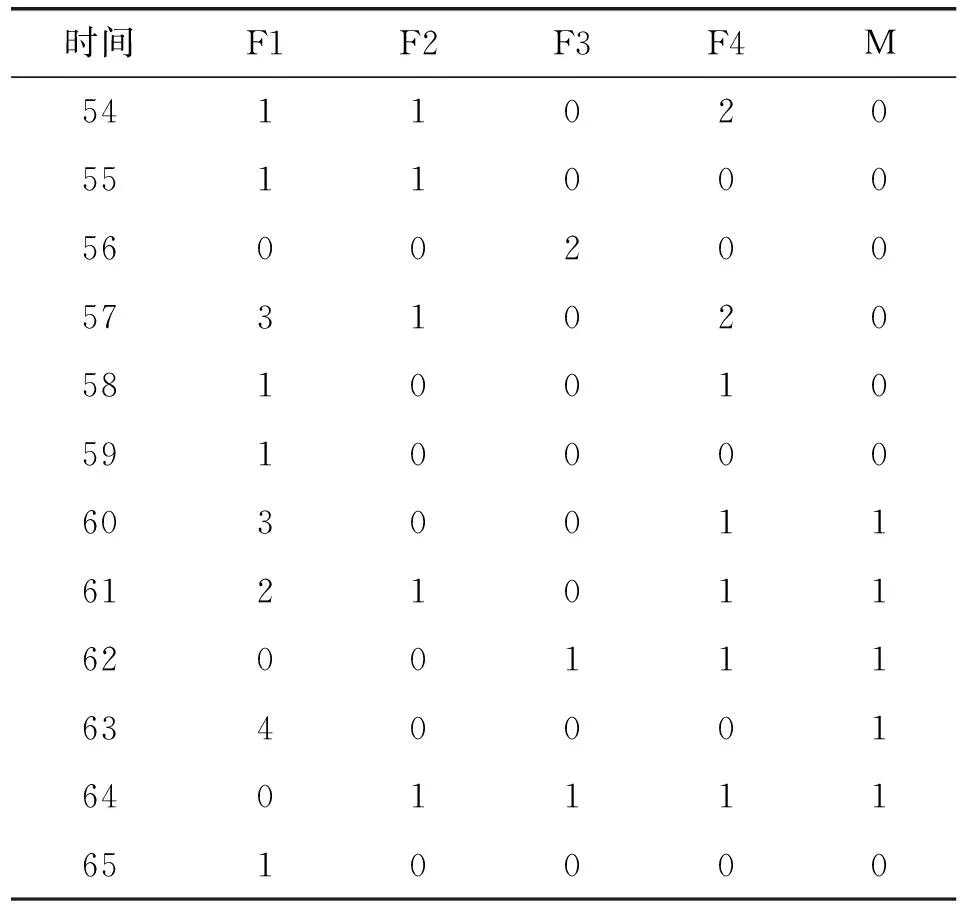
本文所需的故障数据来源于Tomcat 5的用户缺陷跟踪系统https://bz.apache.org/bugzilla/。Tomcat 5的缺陷跟踪系统中组件字段共包含Catalina、Connector、Jasper、Native、Servlets、Webapps、Unknown等属性。根据不同的组件分类,分别提取了每个组件长达65个月的失效数据,如表1所示。表1中观测的时间区间为2004年8月至2009年12月共计65个月(1~65代表第1个月到第65个月),F1代表Catalina组件的失效数,F2代表Connector组件的失效数,F3代表Jasper组件的失效数,F4代表Native、Servlets和Webapps三个组件的失效数,M代表Masked或者Unknown(屏蔽失效数)。
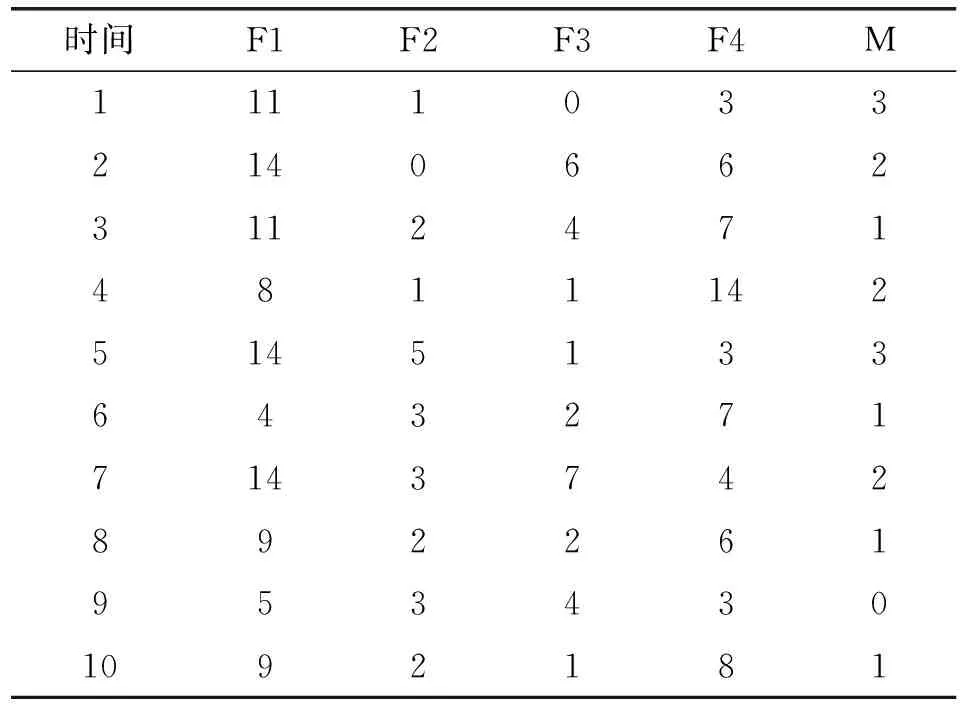
表1 Tomcat 5软件屏蔽失效数据
续表1
续表1
4.2 模型性能对比分析
根据2.1节的变点估计方法,使用Tomcat 5失效数据画出C-Chart图,如图2所示。可以看出,从第33个月开始,超过8个失效数据连续出现在中心线的同一侧,因此我们确定该数据的变点位置为τ=33。因此,下面我们将65个月的失效观测时间分为两个区间[0,33]∪(33,65]分别进行参数估计。
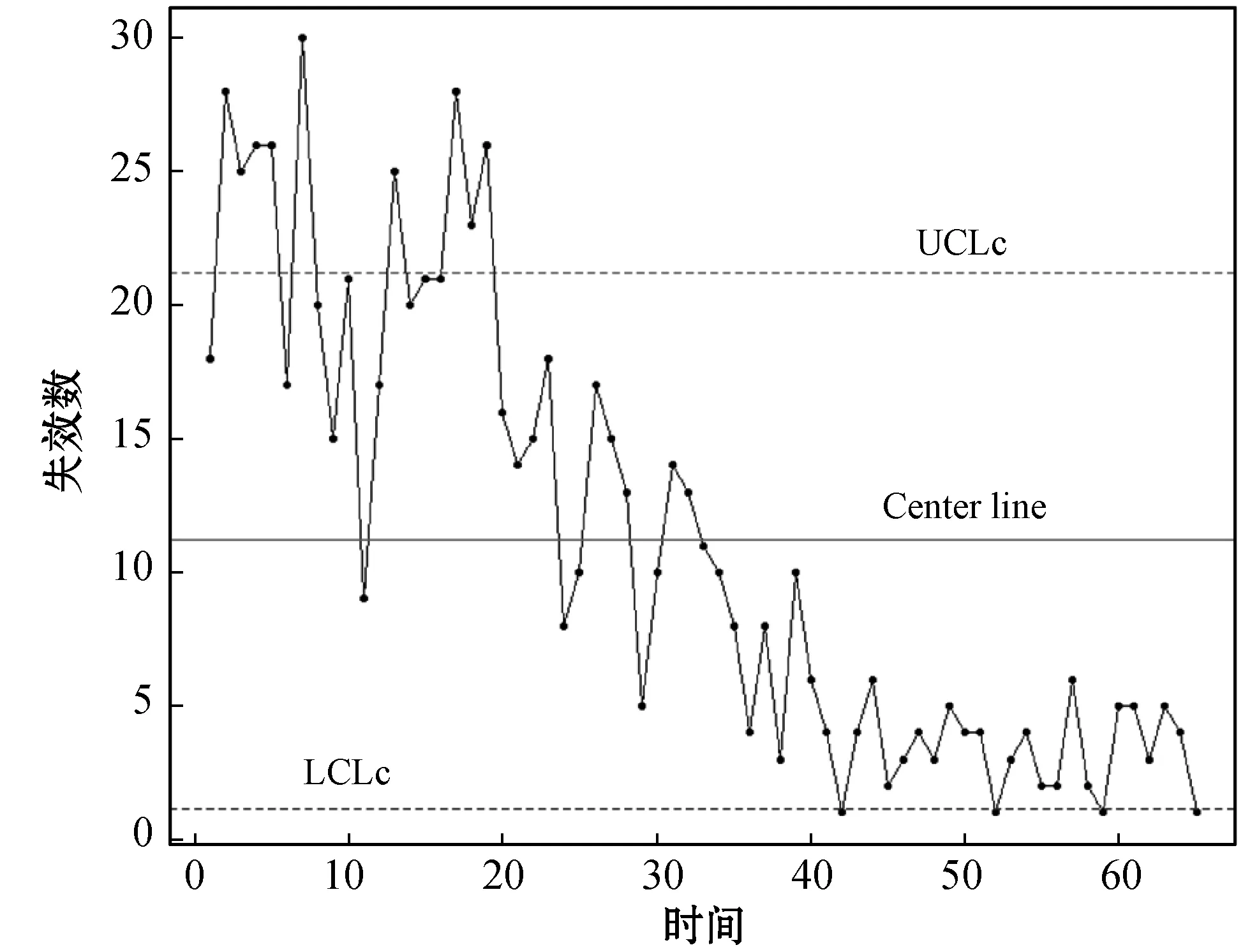
图2 软件失效的C-Chart图
通过上面建立的模型、极大似然估计方法以及EM算法步骤,使用上面的真实数据可以得到表2所示的参数估计结果及模型的均方误差。可以看出,有屏蔽失效的G-O模型的MSE(353.8177)和有变点的G-O模型的MSE(66.4551)比传统G-O模型的MSE(671.4083)都要小,这说明考虑变点和屏蔽失效情况,比传统的G-O模型都有所改进,拟合效果更好。从表2可以进一步看出,屏蔽失效下带变点的G-O模型的MSE(64.0518)比有屏蔽失效的G-O模型的MSE(353.8177)和有变点的G-O模型的MSE(66.4551)都要小,这说明本文提出的可靠性模型具有较好的效果。

表2 参数估计结果及均方误差
图3给出了传统G-O模型、有变点的G-O模型、有屏蔽失效的G-O模型和屏蔽失效下带变点的G-O模型(本文提出的模型)4个模型下的失效数据拟合图。
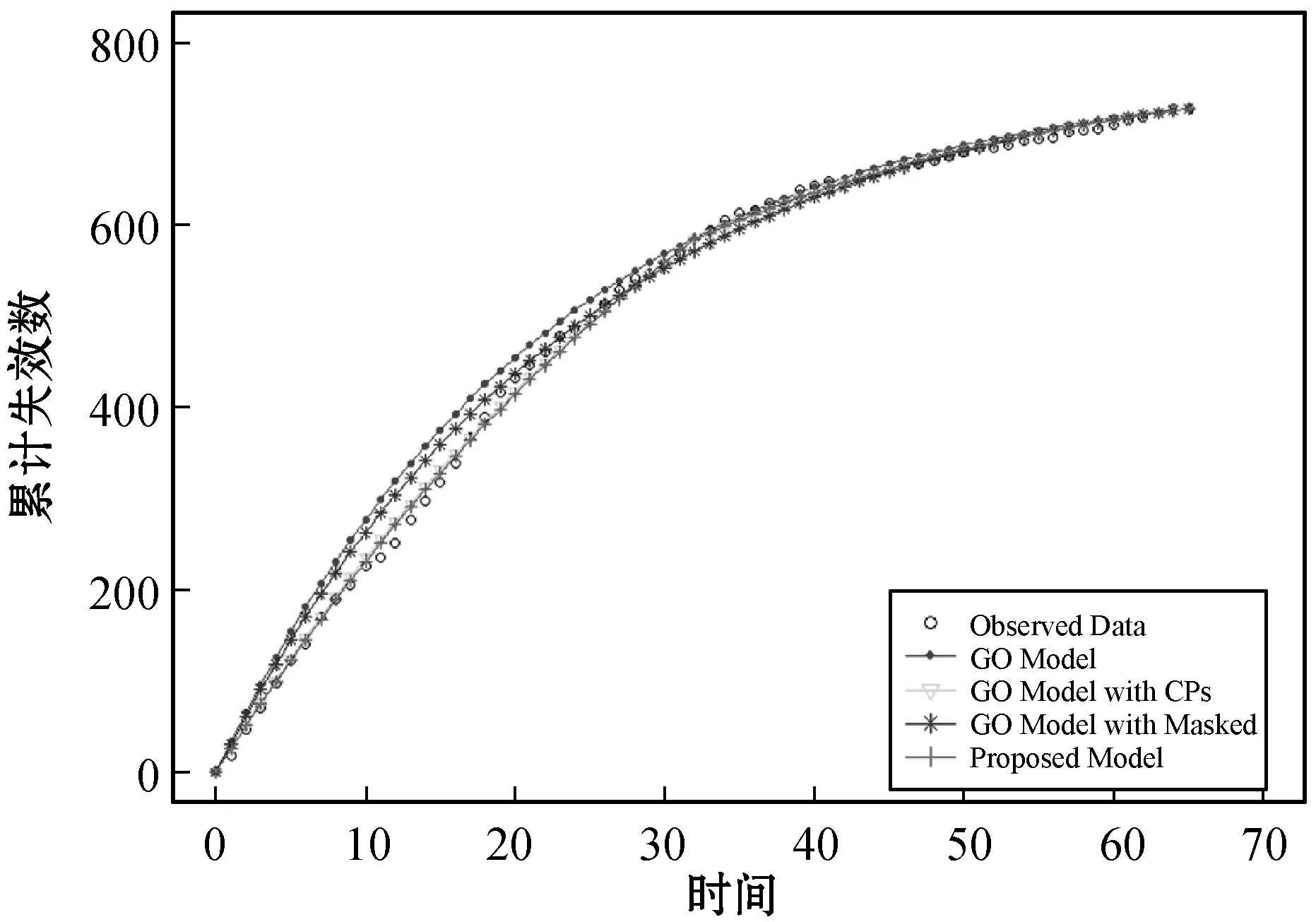
图3 各模型的失效拟合图
5 结 语
本文在考虑屏蔽失效和多变点的情况下,建立了基于非齐次泊松过程的软件可靠性增长模型,详细推导了模型参数的极大似然过程,并利用EM算法解决似然函数极其复杂的问题。为了验证模型的有效性,本文从Tomcat 5缺陷报告系统中提取了65个月的屏蔽失效数据,并利用该真实数据,对提出的模型进行性能对比分析。实验结果表明本文提出的屏蔽数据下带变点的G-O可靠性模型拟合效果最好,其次是带变点的G-O模型和屏蔽数据下的G-O模型,传统的G-O模型效果最差。
