采煤机摇臂用数字液压缸反馈机构间隙问题研究

齐潘国 刘政奇 赵丽薇 张兴元 赵丽娟

辽宁工程技术大学机械工程学院，阜新，123000

0 引言

带有数字化接口的数字液压缸具有结构简单、抗污染、控制精度高、成本低等优点。采用数字液压缸驱动采煤机截割滚筒摇臂，不但能精确控制采煤机截割滚筒的位置，实现自动化和智能化采煤[1]，而且能显著提高采煤机液压系统的简捷性、抗污性及可靠性，进而提高采煤过程的安全性和采煤效率[2-5]。

采煤机摇臂用数字液压缸间隙环节多、工况恶劣、载荷复杂，其反馈机构(采用折返结构的三齿轮反馈机构)间隙不但会引起静态误差，还可能造成系统自持振荡，影响主机的工作效率及可靠性，因此有必要深入研究反馈机构间隙对系统的静态误差及闭环稳定性的影响。

刘有力等[6]综合考虑步进电机旋转、丝杠螺旋反馈和液压缸上的摩擦力等非线性因素，建立了数字液压缸的非线性模型，重点分析了定位精度的影响因素。徐世杰等[7]在考虑输入的饱和特性和数字液压缸的模型非线性基础之上，设计了非线性控制器和抗饱和补偿器，提高了系统的稳定性和动态特性。陈佳等[8]发现数字液压缸在换向时容易产生速度抖动，并且反向运动换向平稳性优于正向运动换向平稳性。

吕凌亘[9]以迟滞间隙模型描述反馈通道间隙，建立了反馈通道含间隙的电液位置伺服系统的模型，研究了反馈通道间隙对系统的稳定性和控制精度的影响。魏列江等[10]针对电液位置伺服系统工程实例，建立了反馈通道含有迟滞间隙特征的电液位置伺服系统的数学模型，发现间隙从小到大变化时，系统单位阶跃响应调节时间明显加长，超调量逐渐增大，出现极限环振荡。李娜娜[11]发现液压缸活塞杆耳环与负载之间的球铰连接处存在间隙，该间隙会增大系统单位阶跃响应的稳态误差和超调量，严重时使控制系统工作失效。

综上所述，对间隙问题的研究多限于电液伺服系统，针对数字液压缸的很少，而且采用的是迟滞间隙模型，没有考虑间隙的刚度和阻尼特性。目前，采煤机摇臂用数字液压缸间隙问题的研究未见文献报道。本文通过理论分析、AMESim仿真及实验来研究采煤机摇臂用数字液压缸间隙问题。先采用描述函数法从理论上分析反馈机构间隙对系统稳定性的影响，再采用静态分析的方法推导反馈机构间隙引起的静态误差的数学表达式，揭示静态误差的影响因素及规律，最后通过仿真和试验验证理论分析的正确性。

1 采煤机摇臂用数字液压缸结构原理

如图1所示，采煤机摇臂用数字液压缸是一种内部机械反馈的液压伺服控制机构，它由伺服电机、滑动联轴器、四边控制阀、机械位置反馈机构和液压缸组成，其中，机械位置反馈机构包括滚珠丝杠、齿轮传动机构及阀芯反馈机构。滚珠丝杠的螺母与活塞固定，丝杠与活塞构成活塞螺纹副。传动比为1的齿轮传动机构包含3个齿轮形成的齿轮传动副，输入端齿轮与丝杠固连，输出端齿轮通过反馈螺母与阀芯一端的螺纹连接，形成阀芯螺纹副。阀芯另一端与伺服电机输出轴通过滑动联轴器相连，阀芯相对电机轴仅能轴向移动，形成阀芯滑动副。

图1 采煤机摇臂用数字液压缸Fig.1 Digital hydraulic cylinder for shearer rocker arm

伺服电机停止不动时，阀芯处于零位，在零开口四边滑阀的控制下，液压缸有杆腔与无杆腔的压力相等，活塞杆停止不动。伺服电机驱动阀芯顺时针(从电机轴端看)转动某一角度后，在阀芯螺纹副的作用下，阀芯轴向移动，阀口打开，液压缸有杆腔压力升高、无杆腔压力降低，活塞及活塞杆回缩。丝杠在活塞螺纹副作用下转动，通过齿轮传动机构带动反馈螺母顺时针转动，在阀芯螺纹副的作用下，阀芯反向移动，阀口开始减小。阀口完全关闭时，活塞及活塞杆停止运动，活塞及活塞杆的回缩位移与电机顺时针转角大小成正比。电机逆时针转动时，液压缸伸出且伸出位移与电机转角成正比，因此通过控制电机的转角可以精确控制液压缸活塞杆的伸出量或缩回量。

2 数字液压缸建模

首先建立反馈机构动力学模型、伺服电机模型、非对称阀控制非对称缸式液压动力机构模型，然后建立数字液压缸模型。

2.1 反馈机构非线性动力学模型

反馈机构非线性动力学分析如图2所示，4个异形空白图形分别代表阀芯、刚性连接的反馈螺母和输出端齿轮、刚性连接的输出入端齿轮和丝杠、活塞。伺服电机输出轴与阀芯构成阀芯滑动副，阀芯与反馈螺母构成阀芯螺纹副，输出端齿轮与输入端齿轮构成齿轮传动副，丝杠和活塞构成活塞螺纹副。图2为4个间隙沿圆周方向的展开图，间隙接合面的接触特性由集中参数的弹簧阻尼模型表征，箭头指向为正方向。

图2 反馈机构非线性动力学分析图Fig.2 Nonlinear dynamics analysis diagram of feedback mechanism

伺服电机输出轴通过阀芯滑动副带动阀芯按图2中θv方向旋转，阀芯螺纹副间隙减小，螺纹接合面接触后产生垂直于接合面的支持力Fnv和平行于接合面的摩擦力Ftv，此时活塞不动，丝杠及齿轮不转动；阀芯在Fnv的作用下按图2中xv方向移动，阀口打开，液压缸两腔的压力差升高，活塞向右运动，活塞内螺纹按图2中xp方向移动，活塞内螺纹接合面越过间隙，与丝杠外螺纹接合面接触后，在活塞螺纹副两接合面的正压力Fnp的作用下丝杠按图2中θp方向旋转，齿轮传动副及阀芯螺纹副依次越过间隙，阀芯螺纹副接合面再次接触后产生与图示Fnv方向相反的支持力，迫使阀芯以与xv运动相反的方向移动，当阀芯再次返回零位时，活塞停止在新的位置。

由上述分析过程可知，阀芯滑动副、阀芯螺纹副、齿轮传动副和活塞螺纹副的间隙影响闭环控制过程。一方面，伺服电机输出轴的转动经过阀芯滑动副和阀芯螺纹副的2个间隙后才能使阀芯轴向移动，打开阀口，从而使活塞杆移动，造成系统响应的延迟。另一方面，越过活塞螺纹副、齿轮传动副和阀芯螺纹副的3个间隙后，活塞的运动才能转化为阀芯的反向移动，形成反馈回路，这会造成反馈的延迟，影响闭环稳定性。阀芯位于阀芯滑动副、阀芯螺纹副之间，反馈螺母位于阀芯螺纹副、齿轮传动副之间，丝杠位于齿轮传动副、活塞螺纹副之间，因此反馈机构有可能发生振荡，其中，阀芯的轴向振动会引起整个闭环系统的振动。

数字液压缸的反馈机构的4个间隙分别为阀芯滑动副间隙、阀芯螺纹副间隙、齿轮传动副间隙和活塞螺纹副间隙。传动系统中应用的非线性间隙模型主要有间隙“死区”模型、间隙“迟滞”模型和间隙“振-冲”模型[11]。间隙“死区”模型的输入为相对位移，输出为力，根据接合面刚度和阻尼大小，将相对位移转换为力，以反映主动部分与从动部分的力传递关系。主动部分在越过间隙过程中，从动部分不一定是静止不动的。间隙“迟滞”模型假设主动部分在越过间隙过程中，从动部分是静止不动的，不考虑主动部分和从动部分之间的动力学过程，模型的输入输出均为位移，反映系统输入与输出的位移关系。间隙“振-冲”模型包括刚性冲击和弹性冲击模型，分析过程很复杂，多被用于动力学和运动学的分析[11]。

阀芯螺纹副间隙的主动部分是阀芯或输出端齿轮的转动，从动部分是阀芯的移动。阀芯的惯性及阻尼都较小，螺纹副的2个接合面有可能因碰撞而脱离，即主动部分在越过间隙过程中，从动部分不一定是静止不动的，因此，间隙非线性模型采用间隙“死区”模型比较合适。同理，阀芯滑动副、齿轮传动副和活塞螺纹副也应采用间隙“死区”模型。

2.1.1阀芯滑动副

阀芯滑动副相邻接触面的相对位移为

zvg=(θτ-θv)rτ

(1)

式中，θτ为伺服电机的转角，rad；θv为阀芯的转角，rad；rτ为伺服电机轴半径，m。

垂直于阀芯滑动副接触面的支持力为

(2)

式中，kvg为阀芯滑动副两接触面接触刚度；Bvg为阀芯滑动副的两接触面接触阻尼；bvg为阀芯滑动副间隙。

平行于阀芯滑动副接触面的摩擦力只考虑静摩擦和库仑摩擦，则相邻牙面的摩擦力为

(3)

式中，μvg，k、μvg，s分别为阀芯滑动副两接触面的动摩擦因数和静摩擦因数；Fin为阀芯滑动副两接触面静摩擦力。

2.1.2阀芯螺纹副

阀芯螺纹副内外螺纹相邻牙面的垂直距离为

(4)

阀芯螺纹副内外螺纹相邻牙面的相对位移为

(5)

阀芯螺纹副相邻螺纹牙面的支持力为

(6)

式中，kvs为阀芯螺纹副相邻牙面间的接触刚度；Bvs为阀芯螺纹副相邻牙面间的接触阻尼；bvs为阀芯螺纹副间隙(包含反馈螺母轴承的游隙)。

平行于内外螺纹相邻牙面的摩擦问题比较复杂，因此采用静态模型即只考虑静摩擦和库仑摩擦，并认为静摩擦因数与库仑摩擦因数相等，则相邻牙面摩擦力为

(7)

式中，μvs，k、μvs，s分别为阀芯螺纹副两接触面的动摩擦因数和静摩擦因数；Ftn为阀芯螺纹副静摩擦力。

采用四边滑阀控制差动液压缸式的液压动力机构，液压缸活塞移动时可以认为总有一对阀口开启，阀芯上作用着与阀芯位置相关的稳态液动力和与阀芯移动速度相关的瞬态液动力。另一对处于负开口(正重叠)状态的阀口引起的液动力可忽略不计。

稳态液动力是一种液体流动引起的回中弹性力，它的表达式为

(8)

式中，W为面积梯度；ps为供油压力；pL为负载压力；rc为阀芯径向间隙。

若忽略阀芯的配合间隙，则稳态液动力简化为

Fsy=ksyxv

(9)

式中，ksy为引起稳态液动力的弹性刚度。

瞬态液动力是一种阻尼力，其大小与阀芯移动速度正比，方向取决于正负阻尼长度差，因此阀芯上的瞬态液动力为

(10)

所以稳态液动力及瞬态液动力之和为

Fyd=Fsy+Fdy

(11)

阀芯的2个台肩与阀体之间存在液压卡紧力，阀芯在阀体内转动和移动要克服摩擦力，摩擦力的大小与液压卡紧力成正比，方向与阀芯台肩的运动方向相反。因此采用静态模型即只考虑静摩擦力、库仑摩擦力和黏性摩擦力，则作用在阀芯上的轴向摩擦力为

(12)

式中，Fk为液压卡紧力；Ffn为阀芯移动静摩擦力；μv，k、μv，s分别为阀芯移动的动摩擦因数和静摩擦因数。

作用在阀芯上的周向摩擦力矩为

(13)

作用在阀芯每个台肩上的液压卡紧力为

Fk=0.27λkLDpL

(14)

式中，λk为台肩上的均压槽个数；L为台肩密封长度；D为阀芯直径。

阀芯移动的力平衡方程的拉氏变换式为

Fnvcosαv=mvXvs2+BvpXvs+KsyXv+

Ftvsinαv+Ftg+Fdy+Ffv

(15)

式中，mv为阀芯质量；Bvp为阀芯的黏性阻尼系数；s为复数变量；Xv为阀芯位移xv的拉氏变换。

阀芯转动的力矩平衡方程的拉氏变换式为

rτFng=Jvθvs2+Bvzθvs+

rv(Fnvsinαv+Ftvcosαv)+Tfv

(16)

式中，Jv为阀芯转动惯量；Bvz为阀芯转动的黏性阻尼系数。

2.1.3齿轮传动副

为方便研究，将齿轮传动机构3个齿轮间的2个间隙等效为1个间隙，则齿轮传动副相邻齿面法向相对位移为

(17)

式中，θp为滚珠丝杠转角；rb为齿轮半径。

齿轮传动副相邻齿面的支持力为

(18)

式中，kvb为齿轮传动副相邻齿面间的接触刚度；Bvb为齿轮传动副相邻齿面间的接触阻尼；bvb为齿轮传动副间隙。

齿轮传动机构的输出端齿轮与反馈螺母固连在一起，二者固连体的力矩平衡方程的拉氏变换式为

(19)

式中，Jb为反馈螺母及输出齿轮的转动惯量；Bb为黏性阻尼系数。

2.1.4活塞螺纹副

活塞螺纹副内外螺纹相邻牙面的法向相对位移zps和切向相对位移yps分别为

zps=xpcosαp-θprpssinαp

(20)

yps=xpsinαp+θprpscosαp

(21)

式中，xp为活塞位移；αp为滚珠丝杠螺旋升角；rps为滚珠丝杠半径；θp为滚珠丝杠转角。

活塞螺纹副内外螺纹相邻牙面之间的法向支持力为

(22)

式中，kps为活塞螺纹副两接触面接触刚度；Bps为活塞螺纹副两接触面接触阻尼；bps为活塞螺纹副间隙(包含丝杠轴承的游隙)。

平行于内外螺纹相邻牙面的摩擦问题比较复杂，因此采用静态模型即只考虑静摩擦和库仑摩擦，则相邻牙面摩擦力为

(23)

式中，Fpn为活塞螺纹副两接触面静摩擦力；μps，k、μps，s分别为活塞螺纹副两接触面的动摩擦因数和静摩擦因数。

丝杠的周向摩擦力矩与2个螺纹副和推力轴承处的摩擦力有关，而推力轴承的摩擦力是主要因素。无杆腔的油液压力作用在丝杠位于活塞孔内的端面上，从而使轴承压紧，故丝杠的周向摩擦力矩为

(24)

式中，p1为无杆腔压力；A1为无杆腔活塞面积；Tpn为活塞螺纹副周向静摩擦力矩；μs，k、μs，s分别为丝杠转动的动摩擦因数和静摩擦因数。

丝杠和与之相连的输入齿轮的力矩平衡方程的拉氏变换式为

rpsFnpsinαp=Jpθps2+Bpθps+rpsFtpcosαp+

Tfs+rbFvb

(25)

式中，Jp为滚珠丝杠和输入齿轮的转动惯量；Bp为黏性阻尼系数。

2.2 伺服电机模型

伺服电机控制采用位置环和电流环的控制。电流环频宽主要受电气时间常数及PWM控制器的开关频率等限制[12-13]。伺服电机电流环的频带为80～100 Hz，因此可将电流环的传递函数简化为比例环节。伺服电机的简化方块图(图3)中，G1为位置环比例控制器，Km为电机转矩常数，TL为外负载转矩，Jτ为电机的转子惯量，Bτ为转子黏性阻尼系数。

图3 伺服电机方块图Fig.3 Bblock diagram of servo motor

2.3 非对称阀控非对称缸模型

采煤机摇臂用数字液压缸的液压动力机构采用的是非对称四边滑阀和非对称式的单杆液压缸，其工作原理如图4所示[14]。非对称式四边滑阀的线性化流量方程的拉氏变换为

图4 非对称四边滑阀控制的非对称式液压缸原理图Fig.4 Schematic diagram of asymmetric hydraulic cylinder controlled by asymmetric four side slide valve

QL=KqXv-KcpL=(Q1+mQ2)/(1+m2)

(26)

式中，QL为负载流量；Q1为无杆腔流量；Q2为有杆腔流量；m为有杆腔与无杆腔有效面积之比；pL为负载压力，pL=p1-mp2；p1为无杆腔压力；p2为有杆腔压力；Kc为流量压力系数。

液压缸的流量连续性方程的拉氏变换为

(27)

式中，Ce为非对称缸的泄漏系数；Vt为非对称式液压缸的总容积；K为有效体积弹性模量。

液压缸的总流量压力系数为

Kce=Kc+Ce

(28)

活塞杆的力平衡方程的拉氏变换为

A1pL=mtXps2+BtXps+FL+Fnpcosαp+Ftpsinαp

(29)

式中，mt为活塞和负载的总质量；Bt为活塞黏性阻尼系数；FL为活塞与缸筒间的摩擦力。

由式(1)～式(29)可得数字液压缸非线性方块图(图5)。由于篇幅有限，方块图中一些引入引出项用字母表示。

图5 数字液压缸非线性方块图Fig.5 Nonlinear block diagram of digital hydraulic cylinder

3 反馈机构间隙对稳定性的影响

3.1 反馈机构间隙的描述函数

描述函数法是分析非线性控制系统的一种近似方法，具有应用简便的优点，且系统阶数不受限制。应用描述函数法对非线性系统进行分析时，通常认为只有输出函数中的基波分量是有意义的，高次谐波分量的振幅通常较小，经过线性系统的低通滤波后衰减殆尽，对系统输出基本无影响。采煤机滚筒摇臂用数字液压缸具有低通滤波性，因此可用描述函数法分析反馈机构间隙对数字液压缸稳定性的影响。

设死区宽度为ε，其静特性如图6a所示，死区的输入信号e(t)=Asinωt(A为正弦幅值，ω为正弦频率，t为时间)时，其输出信号为不连续正弦波，如图6b所示，由sinα0=ε/A可得

(a)死区非线性的静特性 (b)死区正弦输入与输出图6 死区非线性特性Fig.6 Nonlinear characteristics of dead zone

α0=arcsin(ε/A)

(30)

令阀芯螺纹副内外螺纹相邻牙面垂直距离zvs=Asinα=Asinωt，根据式(6)可得阀芯螺纹副相邻牙面的支持力Fnv的输出信号数学表达式：

Fnv(t)=Fnv(t+2π/ω)=

(31)

ε=bvs/2

Fnv(t)的傅氏展开式的基波分量为

(32)

(33)

(34)

将式(30)、式(31)代入式(33)、式(34)可得

(35)

(36)

阀芯螺纹副的描述函数为

Nvs(A)=(B1+jC1)/A

(37)

将式(35)、式(36)代入式(37)可得

(38)

同理可得阀芯滑动副间隙的描述函数Nvg(A)、齿轮传动副间隙的描述函数Nvb(A)和活塞螺纹副间隙Nps(A)：

(39)

(40)

(41)

3.2 数字液压缸稳定性分析

非线性系统经过谐波线性化后等效的线性系统如图7所示，其中，N(A)为非线性元件的描述函数，可以看作数字液压缸间隙“死区”模型的描述函数；G1(s)为系统线性部分传递函数，可以看作数字液压缸除间隙之外的线性传递函数。

图7 等效线性系统方块图Fig.7 Equivalent linear system block diagram

图7所示系统的闭环频率响应可以表示为

(42)

由式(42)可得系统的特征方程：

1+N(A)G1(s)=0

(43)

即有

G1(s)=-1/N(A)

(44)

与线性系统相比，-1/N(A)的轨迹相当于复平面的(-1，j0)点，因此在复平面上同时画出G1(s)和-1/N(A)的曲线，根据两条曲线的位置判断系统的稳定性，以及是否存在自激振荡。若线性部分的的轨迹不包围-1/N(A)轨迹，那么非线性系统稳定，反之不稳定；若线性部分的轨迹与-1/N(A)轨迹相交，那么系统的输出会出现极限环振荡(自持振荡)。

数字液压缸反馈机构间隙特性的描述函数确定后，其负倒频曲线-1/N(A)就确定了。数字液压缸的动力学模型十分复杂，在判断反馈机构间隙对数字液压缸稳定性的影响时，对反馈机构4个间隙逐一进行分析，在频域上依次比较每个间隙的负倒频曲线和除此间隙之外的线性部分奈奎斯特曲线的位置关系。

对包含反馈机构间隙的数字液压缸的方块图进行化简时，各个子模块之间的复杂关系使得化简过程非常繁琐，很难将数字液压缸模型中的线性部分和非线性部分分开。因此使用SIMULINK对数字液压缸线性部分进行编译，以非线性元件的输出为线性部分的输入，以非线性元件的输入为线性部分的输出，得到数字液压缸线性部分的奈奎斯特曲线。绘制数字液压缸线性部分的奈奎斯特曲线时，数字液压缸的结构参数参见表1。

表1 数字液压缸结构参数Tab.1 Structure parameters of digital hydraulic cylinder

3.2.1阀芯滑动副间隙分析

阀芯滑动副间隙的负倒频曲线和线性部分的奈奎斯特曲线如图8所示，右图为左图的局部放大图，由图8可知，当输入信号幅值A从ε开始增大时负倒频曲线是一条从起始点处向复平面的左侧延伸的直线，其斜率几乎为零，其值为-Bvg/Kvg，3条奈奎斯特曲线没有包围负倒频曲线，也没有与之相交，说明阀芯滑动副间隙不影响系统的稳定性，也不会产生自持振荡。

图8 阀芯滑动副间隙的负倒频曲线及奈奎斯特曲线Fig.8 Negative frequency reversal curve and Nyquist curve of valve core sliding pair clearance

3.2.2阀芯螺纹副间隙分析

阀芯螺纹副间隙的负倒频曲线和线性部分的奈奎斯特曲线如图9所示，由图9可知，当输入信号幅值A从ε开始增大时，负倒频曲线是一条从起始点处向复平面的左侧延伸的直线，其斜率几乎为零，其值为-Bvs/Kvs，3条奈奎斯特曲线没有包围负倒频曲线，也没有与之相交，说明阀芯螺纹副间隙不影响系统的稳定性，也不会产生自持振荡。

图9 阀芯螺纹副间隙的负倒频曲线及奈奎斯特曲线Fig.9 Negative inverted frequency curve and Nyquist curve of valve core thread pair clearance

3.2.3齿轮传动副间隙分析

齿轮传动副间隙的负倒频曲线和线性部分奈奎斯特曲线如图10所示，由图可知，当输入信号幅值A从ε开始增大时，负倒频曲线是一条从起始点处向复平面的左侧延伸的直线，其斜率几乎为零，其值为-Bvb/Kvb，3条奈奎斯特曲线没有包围负倒频曲线，也没有与之相交，说明齿轮传动副间隙不影响系统的稳定性，也不会产生自持振荡。

图10 齿轮传动副间隙的负倒频曲线及奈奎斯特曲线Fig.10 Negative inverted frequency curve and Nyquist curve of gear pair clearance

3.2.4活塞螺纹副间隙分析

活塞螺纹副间隙的负倒频曲线和线性部分奈奎斯特曲线如图11所示，由图11可知，当输入信号幅值A从ε开始增大时，负倒频曲线是一条从起始点处向复平面的左侧延伸的直线，其斜率几乎为零，其值为-Bps/Kps，3条奈奎斯特曲线没有包围负倒频曲线，也没有与之相交，说明活塞螺纹副间隙不影响系统的稳定性，也不会产生自持振荡。

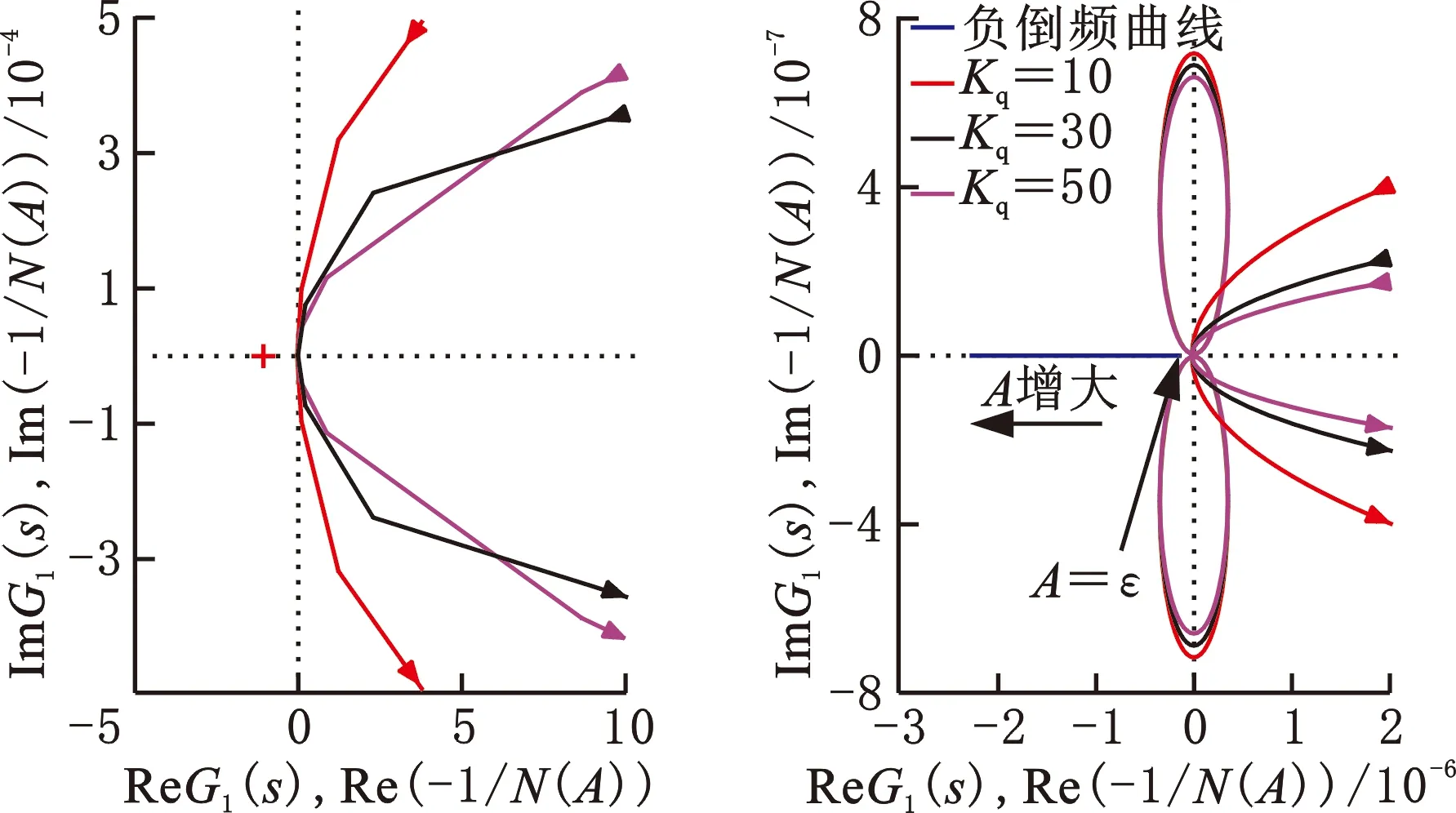
图11 活塞螺纹副间隙负倒频曲线及奈奎斯特曲线Fig.11 Negative inverted frequency curve and Nyquist curve of piston thread pair clearance

4 反馈机构间隙对静态误差的影响

图12 数字液压缸含间隙的静态方块图Fig.12 Static block diagram of digital hydraulic cylinder with clearance

将图12中的4个间隙等效为常值干扰量，干扰的大小与间隙的宽度及运动副的参数有关。下面分别给出阀芯滑动副间隙、阀芯螺纹副间隙、齿轮传动副间隙及活塞螺纹副间隙的等效干扰的表达式。

阀芯滑动副间隙为bvg，伺服电机输出轴的半径为rτ，相当于在输入端加入了角度为Δθvg的常值干扰，易得

Δθvg=bvg/rτ

(45)

同理，将阀芯螺纹副间隙等效为角度为Δθvs的常值干扰，易得

Δθvs=bvs/(rvsinαv)

(46)

将齿轮传动副间隙等效为角度为Δθvb的常值干扰，易得

Δθvb=bvb/rb

(47)

将丝杠螺纹副间隙等效为角度为Δθps的常值干扰，易得

Δθps=bps/(rpsinαp)

(48)

(a)静态方块图

(b)等效变换后的效静态方块图图13 间隙等效为干扰量后的静态方块图Fig.13 Static block diagram after clearance equivalent to interference

Δθ=Δθvg+Δθvs+Δθvb+Δθps

(49)

由图13b可得总干扰误差传递函数：

(50)

则总干扰误差

(51)

阀芯滑动副间隙引起的静态误差为

(52)

式中，pps为丝杠导程。

丝杠导程越小、电机轴半径越大，阀芯滑动副间隙引起的静态误差越小。

阀芯螺纹副间隙引起的静态误差为

(53)

式中，pvg为反馈螺母导程。

反馈螺纹半径和导程越大、丝杠导程越小，阀芯螺纹副间隙引起的静态误差越小。

齿轮传动副间隙引起的静态误差为

(54)

由式(54)可知，齿轮传动副间隙引起的静态误差与齿轮半径成反比，与丝杠导程成正比。

丝杠螺纹副间隙引起的静态误差为

(55)

由式(55)可知，丝杠导程越小、半径越大，活塞螺纹副间隙引起的静态误差越小。

5 仿真验证

根据数字液压缸非线性方块图(图5)，采用AMESim软件搭建数字液压缸的计算机仿真模型，仿真模型参数与试验参数保持一致，见表1。

首先建立含间隙的螺栓螺母模型，如图14所示，右下角的图形为子模型的符号，此模型可以用来研究反馈机构的间隙特性，阀芯螺纹副及活塞螺纹副均采用此模型，只是参数不同。

图14 含间隙的螺栓螺母AMESim模型Fig.14 AMESim model of bolt and nut with clearance

数字液压缸试验采用的插装阀油路块包括1个伺服滑阀、2个液控单向阀、2个溢流阀和2个单向阀，其中，伺服阀为自行设计的非对称四边滑阀，液控单向阀、溢流阀和单向阀均采用SUN Hydraulics公司的插装阀。数字液压缸进油口处加装了1个溢流阀，对数字液压缸起保护作用。液控单向阀的型号是CKEB-XCN，溢流阀的型号是RPEC-LAN，单向阀的型号是CXCD-XCN。液控单向阀、溢流阀和单向阀的AMESim仿真模型均根据样本给出的性能参数曲线进行了有效性验证。采煤机摇臂用数字液压缸AMESim仿真模型如图15所示。

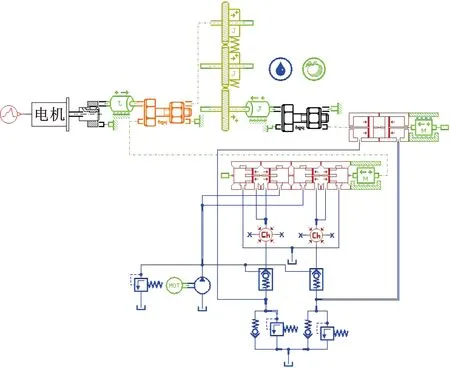
图15 采煤机摇臂用数字液压缸的AMESim仿真模型图Fig.15 AMESim simulation model diagram of the digital hydraulic cylinder for shearer rocker arm

采用仿真模型仿真研究间隙对数字液压缸稳定性及静态误差的影响。设置某个传动副的间隙宽度不为0、其余间隙宽度全为0，对系统输入斜坡信号，考查数字液压缸活塞杆在正向伸出和反向缩回时的稳定性及静态误差，以验证前文对稳定性和静态误差的理论分析结论的正确性。

5.1 阀芯滑动副间隙宽度bvg对静态误差的影响

阀芯滑动副宽度不同的仿真曲线如图16所示，图中蓝色实线为活塞杆的指令输入位移，其他3条曲线是间隙宽度分别0.01 mm、0.1 mm和0.2 mm的活塞杆的输出位移。

由图16可知，活塞杆从中位匀速伸出(电机正向转动)和匀速缩回(电机反向转动)时，活塞杆的输出位移均落后于指令输入位移，且3条输出位移曲线基本重合，这是因为此阶段的误差主要由跟踪误差造成，间隙的影响基本可忽略不计。电机在第3 s正向转动停止，活塞杆停止运动，不受跟踪误差的影响，可以清晰地看到间隙产生的误差，间隙宽度为0.01 mm时，误差基本为0，这与一型系统的无差性是相符的。宽度为0.2 mm时，误差为66μm，根据式(52)计算的误差是63 μm，仿真结果与计算值基本相同。宽度0.1 mm的误差为宽度0.2 mm的误差的一半，这也与理论计算的结果一致。电机在第10 s反向转动停止，活塞杆停止运动，3条输出位移曲线重合，这是由于电机先正向后反向转动，间隙又回到了相同的初始位置。

5.2 阀芯螺纹副间隙宽度bvs对静态误差的影响

阀芯螺纹副间隙宽度不同的仿真曲线如图17所示，图中蓝色实线为活塞杆的指令输入位移，其他3条曲线是间隙宽度分别0.001 mm、0.005 mm和0.01 mm的活塞杆的输出位移。

图17 阀芯螺纹副间隙宽度不为零的活塞杆位移曲线Fig.17 Piston rod displacement curve with the clearance of valve core thread pair

由图17可知，活塞杆从中位匀速伸出(电机正向转动)和匀速缩回(电机反向转动)时，情况与图16基本相同。电机在第3 s正向转动停止，活塞杆停止运动，静态误差为基本为0，这是因为阀芯螺纹副间隙一直保持在初始位置上。电机在第10 s反向转动停止，活塞杆再次停止运动，可以清晰地看到间隙产生的误差，间隙宽度为0.01 mm时，误差为63 μm，根据式(53)计算的误差是67 μm，仿真结果与计算值基本相同。

5.3 齿轮传动副间隙宽度bvb对静态误差的影响

齿轮传动副不同间隙的仿真曲线如图18所示，图中蓝色实线为活塞杆的指令输入位移，其他3条曲线是间隙宽度分别0.5 mm、1.0 mm和1.5 mm的活塞杆的输出位移。

图18 齿轮传动副间隙宽度不为零的活塞杆位移曲线Fig.18 Piston rod displacement curve with the clearance of gear pair

由图18可知，活塞杆从中位匀速伸出(电机正向转动)和匀速缩回(电机反向转动)时，情况与图16基本相同。电机在第3 s正向转动停止后的情况与图17基本相同。电机在第10 s反向转动停止，活塞杆再次停止运动，可以清晰地看到间隙产生的误差，间隙宽度为1.5 mm时，误差为64.5 μm，根据式(54)计算的误差是66 μm，仿真结果与计算值基本相同。

5.4 活塞螺纹副间隙宽度bps对静态误差的影响

活塞螺纹副不同间隙的仿真曲线如图19所示，图中蓝色实线为活塞杆的指令输入位移，其他3条曲线是间隙宽度分别0.01 mm、0.05 mm和0.10 mm的活塞杆的输出位移。

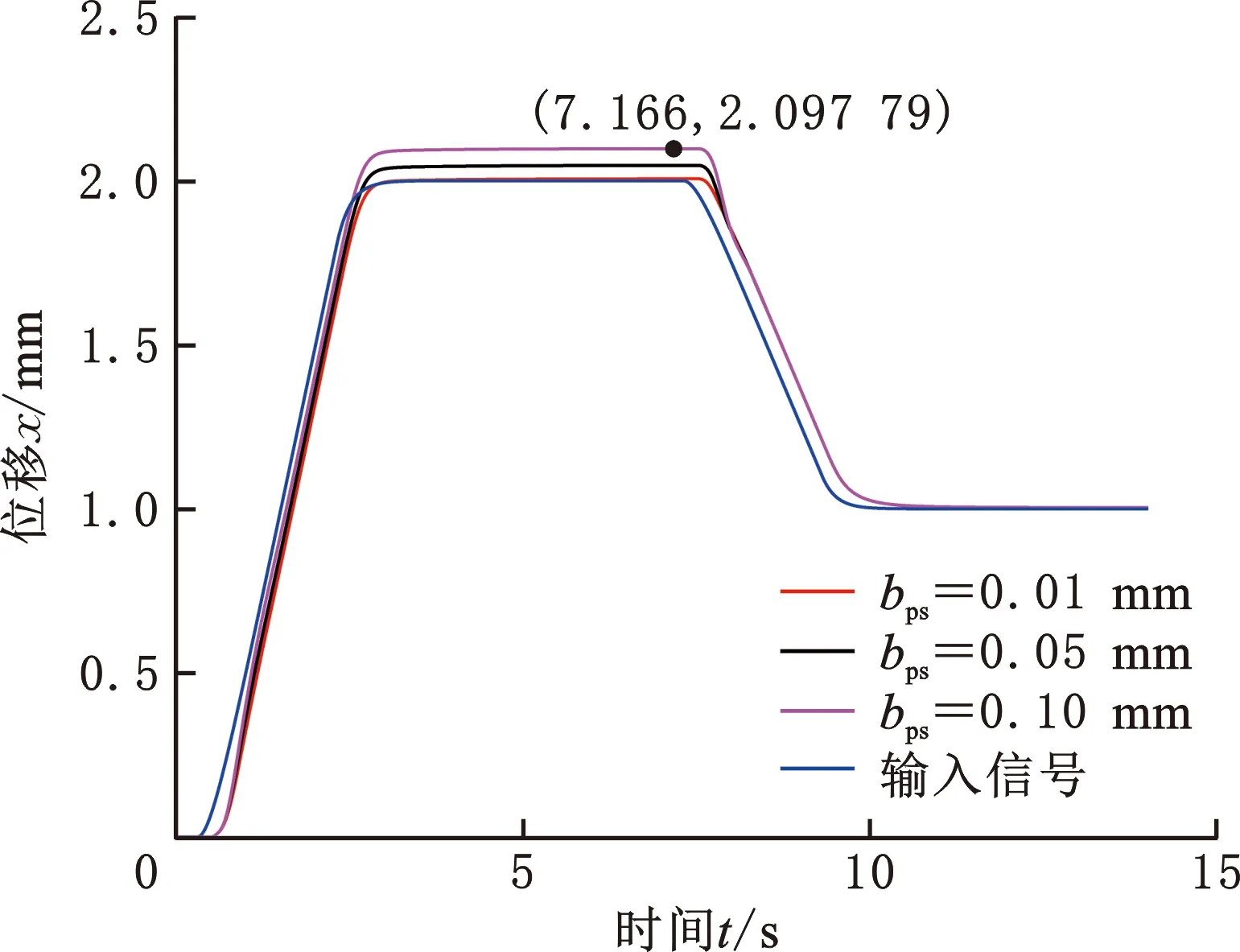
图19 活塞螺纹副间隙宽度不为零的活塞杆位移曲线Fig.19 Piston rod displacement curve with the clearance of piston thread pair

由图19可知，活塞杆从中位匀速伸出(电机正向转动)和匀速缩回(电机反向转动)时，情况与图16基本相同。电机在第3 s正向转动停止，活塞杆停止运动，不受跟踪误差的影响，可以清晰地看到间隙产生的误差，间隙宽度为0.1 mm时，误差为98 μm，根据式(55)计算的误差是105 μm，仿真结果与计算值基本相同。

由以上仿真可见，间隙宽度不同时，系统均可以稳定运行，说明间隙对系统稳定性没有影响，与应用描述函数法的分析结论是一致的。

6 试验验证

2020年9月10日，在西安煤矿机械厂进行了采用数字液压缸驱动1480D采煤机截割滚筒摇臂升降的试验。该数字液压缸最大出力达到1220 kN，缸径320 mm，行程0.78 m，负载质量高达200 t。

如图20所示，采煤机摇臂用数字液压缸试验系统由数字液压缸、机械平台、液压源、传感器、百分表及计算机测控系统组成。检测得到数字液压缸的阀芯滑动副间隙为0.05 mm，阀芯螺纹副间隙为0.04 mm，齿轮传动副间隙为2.1 mm，活塞螺纹副间隙为0.15 mm。为精确测量活塞杆的输出位移，在活塞及缸筒之间安装百分表。

图20 采煤机摇臂用数字液压缸试验系统Fig.20 Test system of the digital hydraulic cylinder for shearer rocker arm

(1)试验1。控制数字液压缸活塞杆先缩回再伸出，得到的实验曲线如图21所示，活塞杆位移仿真曲线与试验曲线基本重合，说明所建立的仿真模型是有效的。由于4个间隙的作用，液压缸活塞杆回缩的3个阶段的输出位移略大于指令输入位移。活塞杆换向伸出后，静态误差较大，约为0.5 mm，这是活塞螺纹副间隙、齿轮传动副间隙及阀芯螺纹副间隙叠加作用的结果，与通过式(49)～式(52)得到的计算结果基本一致。

图21 数字液压缸试验1曲线Fig.21 The test 1 curve of digital hydraulic cylinder

(2)试验2。试验2在试验1的基础上进行，控制数字液压缸活塞杆缩回，得到的实验曲线如图22所示，活塞杆位移仿真曲线与试验曲线基本重合，再次说明所建立的仿真模型是有效的。由于在试验1的基础上进行，因此活塞杆缩回过程中，静态误差继续保持在0.5 mm左右。

图22 数字液压缸试验2曲线Fig.22 The test 2 curve of digital hydraulic cylinder

7 结论

(1)数字液压缸的阀芯滑动副、阀芯螺纹副、齿轮传动副和活塞螺纹副的间隙不影响系统稳定性，但会引起静态误差，误差大小与间隙尺寸成比例。换向时，由于间隙的累积效应，静态误差较大。

(2)丝杠导程越小、电机轴直径越大，阀芯滑动副间隙引起的静态误差越小；丝杠导程越小、反馈螺纹直径和导程越大，阀芯螺纹副间隙引起的静态误差越小；丝杠导程越小、齿轮直径越大，齿轮传动副间隙引起的静态误差越小；丝杠导程越小、直径越大，活塞螺纹副间隙引起的静态误差越小。因此，除了减小间隙外，还可通过减小丝杠导程，增大反馈螺母导程和丝杠、滑动连轴器、反馈螺纹、齿轮直径来减小间隙引起的静态误差。

(3)采煤机摇臂用数字液压缸的定位精度和换向误差试验验证了AMESim仿真模型的有效性和对间隙问题理论分析的正确性。