基于斜角切削理论的钛合金螺旋铣孔切削力建模
2023-02-17王海艳周秩同付麒麟
王海艳 周秩同 武 晔 付麒麟
东北大学秦皇岛分校控制工程学院,河北,066000
0 引言
钛合金因密度小、强度高、耐腐蚀、耐高温等优良特性,常作为航空航天等领域的结构零件或功能零件材料[1]。制孔是结构部件组装前重要的加工操作,但存在轴向力大、散热条件差、制孔质量差等缺点[2-3]。螺旋铣孔作为一种新型制孔加工技术,具有轴向力小、制孔质量高、切削区域不封闭易于排屑和散热、刀具寿命长等优势[4-5]。
切削力建模是预测刀具磨损断裂、机床振动、切削参数优化和表面质量的基础[6],目前的研究中主要采用机械或者力学方法构建切削力模型。李士鹏等[7]研究了切削力和刀具挠曲变形的耦合关系,考虑刀具受力变形规律,构建了基于切削厚度迭代反馈的切削力预测模型。LIU等[8]提出了螺旋铣孔时域切削力模型,研究了切削力与主轴速度、切削深度及铣刀几何形状之间的关系。REY等[9]考虑螺旋铣孔切削机理和刀具几何形状,构建了基于瞬时切屑厚度的切削力模型,并通过螺旋铣孔试验验证了模型的准确性。上述研究均以切削参数为变量,目前针对加工过程中内部物理变量(如剪切角、摩擦角、剪切应力等)变化的研究较少。
切削力模型含有待求的切削力系数,因此准确识别和优化模型中的切削力系数非常关键[10]。现有的研究中,辨识切削力系数的方法有:平均力法、斜角切削法、瞬时力法、优化技术法。王博等[11]运用了平均力系数法识别球头铣刀多轴铣削加工的铣削力系数。SRINIVASA等[12]基于低碳钢工件的材料特性和斜角切削原理,分别采用迭代算法、最小能量原理、JC模型确定了摩擦角、剪切角、剪切应力等参数,构建了微细端面铣削切削力预测模型。LUO等[13]开展了3组直线端铣试验,将剪应力、剪切角、摩擦角标定为瞬时未变形切屑厚度的双指数函数,利用斜角切削力系数识别公式求解切削力,试验结果表明切削力的仿真能够较好地拟合试验值。WANG等[14]构建了螺旋铣孔过程中的线性和非线性切削力模型,并采用瞬时力法和平均力法识别了切削力系数。ADEM等[15]采用优化技术法,通过最小化切削力的试验和预测值的误差来确定切削力系数。
上述求解切削力系数的方法仍然依靠大量的切削试验,利用少量切削试验得到切削力系数的研究较少。因此本文基于螺旋铣孔切削原理,建立了钛合金螺旋铣孔过程的切削力解析模型;开展铣槽试验来标定剪切角、摩擦角、剪切应力,采用斜角切削法求解侧刃六个切削力系数;开展了钛合金螺旋铣孔试验,并采用数据拟合法求解底刃两个切削力系数,切削力仿真值与试验值的对比验证了模型的准确性。
1 螺旋铣孔工作原理
螺旋铣孔过程如图1所示,刀具在自转的同时围绕孔中心公转,并且保持轴向进给,即刀具在自转的同时沿着螺旋线运动。因此,通过改变刀具的偏心距,可以方便地改变孔的加工直径。

图1 螺旋铣孔过程示意图Fig.1 Schematic of helical milling process
螺旋铣孔过程中的主要切削参数有刀具自转速度、公转速度、轴向进给速度、中心进给速度。假设刀具直径为D1,被加工孔直径为D2,主轴自转速度为n1,公转速度为n2,则有
(1)
式中,ω1为刀具自转角速度;ω2为刀具公转角速度。
刀具运动时,设某时间间隔内的自转角度为ξ,公转角度为θ,则有
(2)
式中,ξ0为刀具的初始自转角度;θ0为刀具的初始公转角度;t为运动时间。
刀具中心进给速度为
vo=π(D2-D1)n2
(3)
若刀具齿数为N,则刀具中心的每齿进给量为
(4)
2 切削力建模
螺旋铣孔加工过程中,刀具同时完成自转、公转和轴向进给三种运动,总的切削力是侧刃和底刃产生的切削力之和:
F(t)=Fc(t)+Fd(t)
(5)
式中,Fc(t)为侧刃产生的切削力;Fd(t)为底刃产生的切削力。
2.1 侧刃切削力
在螺旋铣孔过程中,刀具中心始终与被加工孔中心不重合,为方便构建切削力模型,建立工件坐标系OaXaYaZa、刀具坐标系ObXbYbZb,如图1所示。
用半解析法建立切削力模型,假设P点位于第k个切削刃上,P点的轴向高度为z,首先采用微分几何的方法将刀具离散成若干沿轴向分布的微元,然后对每个微元进行分析,分别建立切向、径向和轴向的微元切削力:
(6)
hk(ξ,z)=sosinξk(t)
(7)
(8)
式中,Ktc、Krc、Kac分别为与材料剪切作用相关的切向、径向和轴向的剪切力系数;Kte、Kre、Kae分别为与刀刃摩擦相关的切向、径向和轴向的刃口力系数;dS为离散化的切削弧长,随高度z变化;dz为微元轴向切深;hk(ξ,z)为任意时刻侧刃切削的未变形切屑厚度;ξ1(t)为刀具在初始时刻的自转角度;so为刀具每齿进给量;ξk(t)为刀具在任意时刻的自转角度;i为刀具螺旋角。
2.2 底刃切削力
螺旋铣孔过程中,底刃产生的轴向力比较大、切向力和径向力很微小(可忽略不计)[16],假设由于底刃切削影响的轴向力增加量为Fd(t),则有
Fd(t)=(Kdcsz+Kde)D1/2
(9)
其中,sz为刀具的轴向每齿进给量;Kdc、Kde为与底刃有关的切削力系数,可通过对螺旋铣孔试验所测平均轴向力线性拟合获得。
3 斜角切削几何参数的约束
立铣刀侧刃的切削属于斜角切削,斜角切削中的倾斜角等于立铣刀的螺旋角[17]。螺旋铣孔过程中的微元刃切削状态如图2所示。
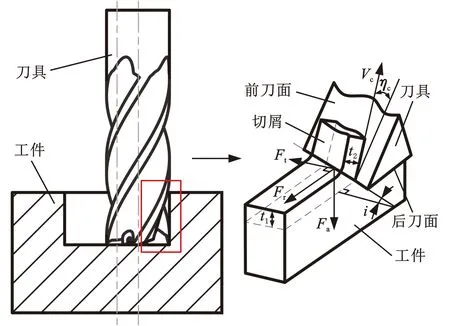
图2 斜角切削原理图Fig.2 Schematic of oblique cutting
在工作法平面参考系中,剪切力系数修正为[13]
(10)
(11)
(12)
(13)
Kte、Kre、Kae可从文献[12]的解析模型中估计:
Kte=reτ(2βn/cosβn+πsinβntanβn)
(14)
(15)
Kae=Ktesini
(16)
式中,αn为法向前角;βn为法向摩擦角;φn为法向剪切角;τ为剪切应力;ηc为切屑流动角;re为刀具刃口半径。
根据Stabler提出的排屑法则,切屑流动角ηc等于倾斜角i[13]。
斜角切削过程中产生了很多空间角度,如图3a所示,引入X、Y、Z轴,切削刃平行于Y轴,垂直于OXZ面。X轴与刀具和工件运动方向夹角为i,剪切面与生成面夹角为φn。斜角切削中,切屑流动方向与切削刃垂直方向的夹角为ηc,法向前角αn在正交平面中测量。另外,为了清楚地显示斜角切削过程,假设切屑没有卷曲的趋势,令切屑被切削前后的厚度比值t1/t2=gt,当gt和αn已知时,法向剪切角可通过下式获得:

(a)斜角切削的几何关系
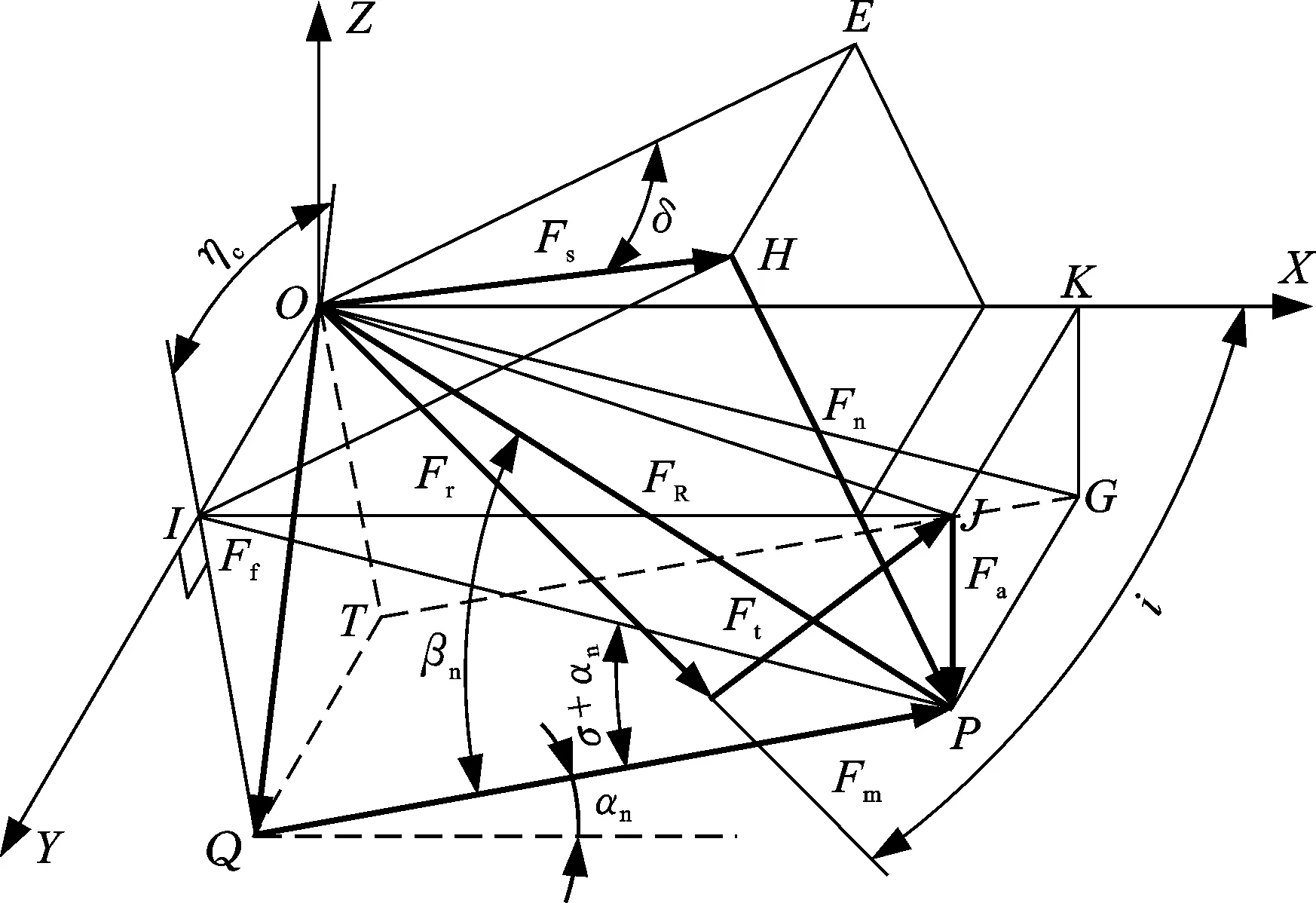
(b)斜角切削的力关系图3 斜角切削过程Fig.3 Oblique cutting process
(17)
斜角切削中,剪切方向与切削刃的垂线方向夹角为δ。由图3a可得ηc与δ的关系:
一天,我正茫然走在大街上时,突然看到了小满。我正要喊她时,不知为什么,小满突然全身着起了火。火势在小满的周身上下蔓延着,小满被烧得在地上痛苦地翻滚……不一会儿,伤痕累累的小满被一辆救护车载着呼啸而去。
(18)
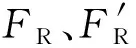
(19)
式中,σ为辅助角度;Fx、Fz分别为X向、Z向的切削力。
摩擦因数为
(20)
摩擦力为
(21)
式中,Fy为Y向的切削力。
剪切力为
(22)
剪切面的剪切应力τ等于金属的平均剪切强度,即有
(23)
式中,A0为切屑的横截面积,A0=t1w;w为刀具切削刃宽度。
4 试验与分析
为验证切削力模型的有效性,首先进行切削力系数标定试验,然后进行钛合金全因子螺旋铣孔试验。试验在五轴加工中心DMU80T上进行,工件材料为钛合金。刀具为四刃专用立铣刀,基体材料为钨钢,涂层材料为 TiAlN,直径为6 mm,螺旋角为30°,前角为5°。切削过程中,Kistler-9257B测力仪采集三向切削力数据,采样频率为10 kHz。
4.1 标定试验
在固定的切削深度ap为2 mm、切削宽度b为6 mm、主轴转速n1为3000 r/min,以及不同的每齿进给量so(0.05 mm、0.06 mm、0.08 mm)下进行3组铣槽切削试验。
槽和切屑如图4所示,用千分尺测量切屑厚度,并将10个切屑厚度的平均值作为试验结果。已知切屑厚度比值gt、Fx、Fy、Fz,根据式(17)~式(23)可解得摩擦角、剪切角、剪切应力等切削参数,将上述参数代入式(10)~式(16),可求得的切削力系数Ktc=1897.4 N/mm2、Krc=67.78 N/mm2、Kac=435.94 N/mm2、Kte=2.90 N/mm、Kre=2.26 N/mm、Kae=1.45 N/mm。

(a)槽 (b)切屑图4 槽和切屑Fig.4 Groove and chip pictures
4.2 钛合金螺旋铣孔试验
为计算底刃切削力系数和验证力预测模型的准确性,开展螺旋铣孔试验。试验采用微量润滑,铣削方式为顺铣,工件、刀具及试验布置如图5所示,试验中选择的切削参数如表1所示。

图5 试验装置Fig.5 Experimental setup

表1 全因子试验数据Tab.1 Full factor experimental data
4.3 试验结果与分析
对钛合金螺旋铣孔切削力进行处理,将得到的轴向切削力平均值代入式(9),求得与底刃有关的切削力系数Kdc=8985.43 N/mm2和Kde=6.5462 N/mm,从而到全部的切削力系数,进而预测切削力。
在收集切削力信号的过程中,由于噪声等外界干扰,采集到的信号比较杂乱,所以使用135 Hz低通滤波器对全局切削力信号进行滤波。图6a所示为主轴转速4500 r/min、刀具中心每齿进给量0.04 mm、轴向切削深度0.2 mm/r条件下低通滤波后的三向切削力,图6b为其在40~42 s的局部放大图。

(a)全局切削力
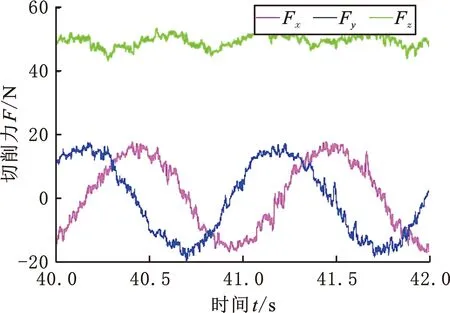
(b)40~42 s切削力图6 低通滤波后的切削力Fig.6 Cutting forces after low-pass filtering
由图6b可以看出,Fx、Fy波动周期相近,且波动很大;Fz处于无周期波动的状态,且其平均值远大于Fx、Fy的平均值。为准确拟合出切削力的极值,将40~42 s内的切削力作为分析依据。
通过标定试验识别出侧刃的6个切削力系数,通过平均切削力拟合的方法识别出底刃的2个切削力系数,将这8个切削力系数代入全局工件坐标系的切削力模型,计算得到切削力的仿真预测值。将低通滤波后的切削力试验值与仿真预测值绘于同一张图内,使两者的初始相位相同,如图7所示。
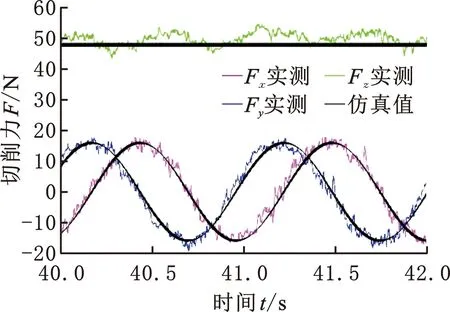
(a)4500 r/min,0.04 mm,0.2 mm/r

(b)4500 r/min,0.06 mm,0.15 mm/r
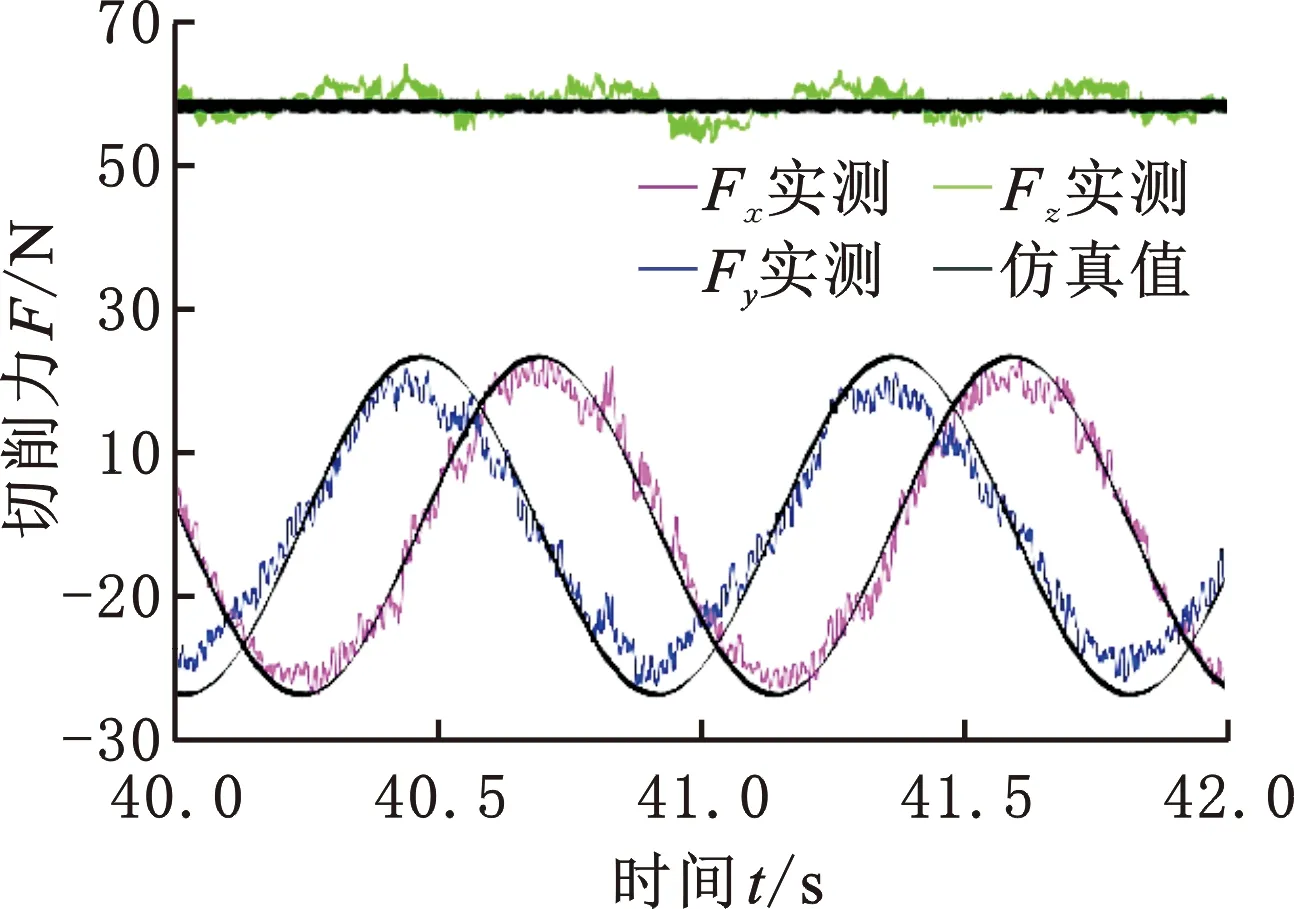
(c)4000 r/min,0.06 mm,0.1 mm/r

(d)3500 r/min,0.08 mm,0.15 mm/r图7 仿真力与试验力Fig.7 Forces of simulation and experiment
从切削力对比结果可以得出,不同切削参数条件下,虽然切削力的仿真值与试验值存在一定的偏差,但是仿真值能捕捉切削力的变化,实时反映切削力的变化,其中,Fx、Fy拟合精度较高,Fz拟合效果不太好。为进一步研究两者之间的偏差大小,根据图7计算出切削力仿真值和试验值的最大值误差,结果如表2所示。其中,最大误差14.16%对应图7a,最小误差3.15%对应图7d,平均误差为9.55%。产生误差的因素如下:测量过程中存在小幅的干扰信号、刀具的制造精度、切削振动、测力系统零点漂移等。总体来看,仿真的切削力基本准确拟合了切削力的变化。
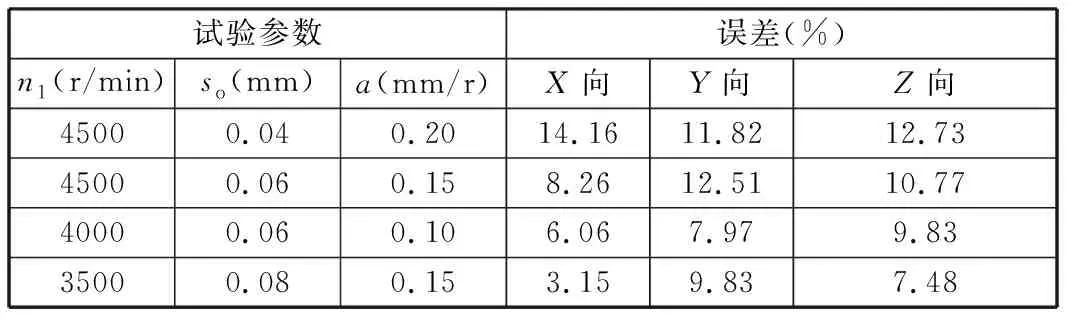
表2 切削力仿真值与试验值的误差Tab.2 Errors between simulation and experimental forces
5 结论
(1)本文从螺旋铣孔工作原理和运动向量出发,考虑侧刃和底刃的作用,建立了钛合金螺旋铣孔切削力的解析模型。
(2)基于斜角切削中几何参数的关系,构建了摩擦角、剪切角、剪切应力的约束方程,开展了钛合金单因素铣槽试验,确定了以上参数并求解出侧刃的切削力系数。基于钛合金螺旋铣孔的试验结果,通过数据拟合的方法预测了底刃的切削力系数。
(3)基于辨识出的8个切削力系数,预测不同切削参数下切削力变化情况。结果表明,仿真结果和试验结果具有较好的一致性,验证了斜角切削系数辨识方法的正确性和切削力模型的可靠性。
