基于自由度约束的元动作单元误差传递路径识别方法

李 健 张根保 冉 琰 王勇勤

重庆大学机械与运载工程学院，重庆，400044

0 引言

机械系统的装配精度对运动性能有显著影响，因此，为保证机械产品的运动性能，需对机械系统的装配精度进行分析，但机械系统结构复杂、零部件众多，传统的精度分析方法使用十分不便。LI等[1]根据机械系统的特点，提出了“功能-运动-动作(function-motion-action，FMA)”的结构化分解方法。该方法将复杂机械系统分解为独立的元动作，并将元动作作为分析的最小单元，保证了元动作的性能就能保证整机的性能。元动作结构相对简单，分析和建模方便，因此在装配误差分析[2]、精度分析预测[3-4]、精度映射[5]、精度分配[6]等领域得到广泛的应用。

元动作单元是机械产品中最小的结构单元，其误差建模和分析是整机精度分析的基础。学者对机械系统的误差分析和建模过程进行了广泛的研究，并提出多种误差建模方法，如三角几何法[7]、神经网络法[7]、多体系统理论法[8-11]和装配有向图法[12]。上述方法在对机械系统进行误差建模的过程中，主要利用机械系统的拓扑结构和装配序列来表达误差的传递路径。机械系统中，一个零件可能与相邻的多个零件存在装配关系，导致存在多条误差传递路径，直接利用拓扑结构和装配序列来表达机械系统中误差的传递路径会导致分析结果不准确。为提高误差建模和分析结果的准确性，搜索和识别合适的误差传递路径至关重要。吕程等[13]研究了复杂机械产品误差传递路径的搜索方法，通过分析典型结合面的误差传递属性，定义结合面的信息集成表达符号，结合多色集合理论，建立了描述装配关系、结合面类型、结合面误差传递属性的结合面符号矩阵，并在此基础上提出了装配体误差传递路径的搜索方法。该方法首先搜索基准件到精度输出件之间所有的误差传递路径，然后将精度输出件误差分量的最短误差传递路径作为最终的误差传递路径。此方法需要遍历搜索所有误差传递路径，计算工作量较大，在实际应用中存在一定局限性。针对元动作单元的结构特点，YANG等[4]提出一种误差传递路径的逆向搜索方法，通过分析元动作单元中零件间的装配关系，建立装配有向图，以精度输出件、支撑件为误差传递路径搜索的起点和终点，逐层定性分析各结合面的误差传递属性，剔除误差传递的中断路径，最终确定误差传递路径，但该搜索方法依然对起辅助作用的零件的误差传递路径进行分析，增加了不必要的分析计算。

本文提出一种基于精度输出件自由度约束判断误差传递路径新方法，通过分析元动作单元中零件的组成和主要功能，初步确定误差传递路径，然后根据误差传递路径中的结合面约束属性，计算得到精度输出件的自由度约束属性，并将其与精度输出件设计要求的自由度约束属性对比，确定误差传递路径。

1 元动作理论介绍

1.1 FMA结构化分解树

元动作理论利用FMA结构化分解树对复杂机械系统进行结构化分解，得到各个串联的元动作，该理论在数控机床可靠性、精度等研究领域得到了广泛应用[14-17]。FMA结构化分解树如图1所示，整机的性能通过各个元动作以及元动作之间连接的性能来实现。从元动作单元入手对机械系统的误差进行建模和分析，可以大大提高分析的效率。

图1 机电产品FMA结构分解树Fig.1 Schematic of the FMA decomposition tree

1.2 元动作分类及其单元的结构组成

元动作根据运动形式的不同分为转动元动作和移动元动作。元动作单元主要由5个要素组成，包括动力输入件、中间件、支撑件、紧固件和动力输出件，其结构模型如图2所示[15]。

图2 元动作单元结构组成Fig.2 The structure of meta-action unit

在元动作单元中，对机械系统的运动精度产生主要影响的是动力输入件和动力输出件的装配精度。因此，对元动作单元进行误差分析时，动力输入件和动力输出件为精度输出件，支撑件为基准键。支撑件、中间件、动力输入件和动力输出件的装配结合面构成了元动作单元的误差传递路径。

2 结合面自由度约束分析

2.1 自由度约束表达

机械系统误差传递分析主要利用小位移弦量(small displacement torsors，SDT)法描述结合面的误差变动[18-19]。若ε=(εx，εy，εz)=(u，v，w)，p=(px，py，pz)=(α，β，γ)，其中，u、v、w分别为沿坐标轴X、Y、Z的移动变化量，α、β、γ分别为绕坐标轴X、Y、Z的转动变化量，则用SDT表示的误差变化量为

T=(ε，p)=(u，v，w，α，β，γ)

(1)

为更加方便地利用SDT模型进行误差分析，吕程等[13]引入二进制数表达方式，即将SDT模型表示的误差变化量的非0元素用1表示，其余元素用0表示。SDT模型的二进制数模型中，为1的元素表示该方向自由度被约束，为0的元素表示该方向自由度没有被约束，因此SDT模型的二进制数模型可方便地表示零件自由度的约束情况，即自由度约束属性。

2.2 典型结合面自由度约束属性

机械系统中，典型的结合面包括平面结合面、圆柱结合面和圆锥结合面。典型结合面对被约束零件的自由度约束属性如表1所示，其中，A为约束零件，B为被约束零件。

表1 典型结合面自由度约束属性Tab.1 Constraint property of DOF fortypical joint surface

2.3 相邻结合面自由度约束属性

机械系统中，相邻结合面分为串联结合面和并联结合面[20]，如图3所示，图中，P1、P2、P3表示零件，F1、F2表示结合面，箭头表示零件的装配顺序。图3a中，零件P1、P2、P3分别通过结合面F1、F2连接，因此结合面F1、F2为串联结合面。图3b中，零件P1、P2同时通过结合面F1、F2连接，此时的结合面P1、P2为并联结合面。

(a)串联结合面 (b)并联结合面图3 串联结合面与并联结合面Fig.3 Series joint surface and parallel joint surface

零件之间通过结合面约束被装配零件的自由度，对于串联结合面，若TF1、TF2分别为零件P2、P3受结合面F1、F2约束时的自由度约束属性，则P3的各个方向自由度的约束情况受F1、F2的共同影响，通过对TF1、TF2进行逻辑“积”运算，得到串联条件下P3的自由度约束属性[13]：

(2)

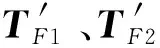
(3)

在机械系统中，常见的并联结合面主要为平面结合面&平面结合面、圆柱结合面&平面结合面、圆柱结合面&圆柱结合面[21-22]。并联结合面对被约束零件的自由度约束属性如表2所示。

表2 并联结合面自由度约束属性Tab.2 Constraint property of DOF for parallel joint surface

元动作单元存在冗余结构时，冗余结构对被约束零件构成并联约束关系，被约束零件的误差受并联约束关系的综合影响，因此可以将冗余结构产生的并联约束关系等同于并联结合面进行处理。

3 元动作单元误差传递路径分析

由元动作单元结构组成可知，元动作单元结构相对简单。通过分析单元中5个组成要素的装配关系，可以很容易得到误差传递路径，即支撑件-中间件-精度输出件(动力输入件和动力输出件)。元动作单元中的中间件较多，分为传递动力和辅助定位两种。选择传递动力的中间件作为误差传递路径中的元素，可得初始误差传递路径，然后对该路径进行分析判断，确定该误差传递路径为所求路径。

3.1 基于自由度约束的误差传递路径分析方法

通过机械系统内部零件之间的装配关系，实现对零件各个方向自由度的约束，未被约束的方向则可实现规定的运动。因此，对于元动作来说，通过单元中各个零件及结合面的装配关系，约束了精度输出件(动力输入件和动力输出件)的5个自由度，而未被约束的运动即为元动作需要实现的运动。对于转动元动作，未被约束的自由度为绕X轴(Y轴或Z轴)的转动；对于移动元动作，未被约束的自由度为沿X轴(Y轴或Z轴)的移动。

3.2 元动作单元误差传递路径分析流程

元动作单元误差传递路径分析流程如图4所示，具体步骤如下：

图4 元动作单元误差传递路径分析流程图Fig.4 Flow chart of error transfer path analysis for meta-action unit

(1)分析元动作功能及元动作单元的结构，将单元中的零件分为支撑件、中间件、紧固件、动力输入件和动力输出件。

(2)确定元动作单元动力输入件和动力输出件的设计运动状态，得到其自由度约束属性T=(T(Ipart)，T(Opart))。

(3)分析元动作单元的支撑件、中间件(传递动力)和精度输出件(动力输入件和动力输出件)，初步确定误差传递路径。

(4)分析误差传递路径中零件间的配合关系，识别零件间的主要结合面。

(5)根据表1和表2，得到各个结合面的自由度约束属性。

(8)输出元动作单元误差传递路径。

4 实例分析

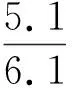
1.螺母 2.输入齿轮 3.键 4.左轴承端盖 5.箱体 6.左轴承 7.轴套 8.传动轴 9.输出齿轮 10.键 11.右轴承 12.右轴承端盖图5 齿轮转动元动作单元结构简图Fig.5 The structure diagram of gear rotation meta-action unit

通过分析齿轮转动元动作单元的结构，确定精度输出件为输入齿轮和输出齿轮，基准件为箱体，主要传递动力的中间件为左轴承、传动轴和右轴承。因此，初步确定单元的误差传递路径：箱体-左轴承/右轴承-传动轴-输入齿轮(输出齿轮)。

误差传递路径中，零件之间的结合面关系以及结合面的自由度约束属性如图6所示。箱体为基准件，6个自由度均被限制，因此规定箱体的自由度约束属性为(1，1，1，1，1，1)；箱体与轴为双支撑结构，包括2条并联的支路径，即箱体-左轴承-传动轴、箱体-右轴承-传动轴。右轴承与传动轴、传动轴与输入齿轮、传动轴与输出齿轮分别有2个相邻结合面，而且它们均为并联关系。因此，利用式(3)的计算方法，得到输入齿轮和输出齿轮的自由度约束属性：

图6 齿轮转动元动作单元误差传递路径Fig.6 Error transmission path of gear rotation meta-action unit

(4)

图7 改进齿轮转动元动作单元误差传递路径Fig.7 Improved error transmission path of gear rotation meta-action unit

(5)

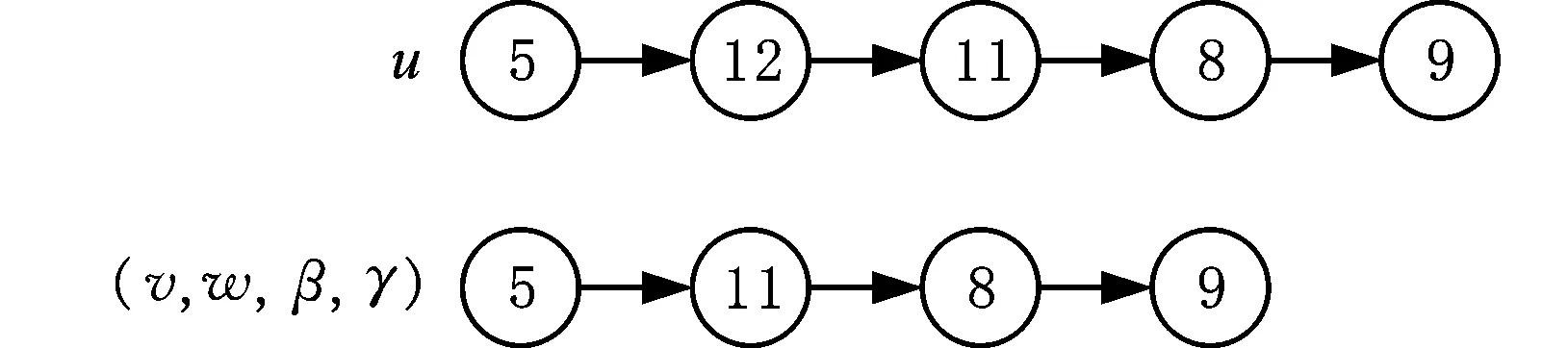
齿轮转动元动作单元的误差项包括输入齿轮和输出齿轮的X向、Y向和Z向的移动误差，以及绕Y轴和Z轴的转动误差。为说明本文方法的优势，利用文献[13]、文献[4]的方法计算齿轮转动元动作单元的输出齿轮各个方向误差的传递路径，然后将其与本文方法所得结果进行对比。为比较各个方法的计算效率，用分析过程中的路径分析总数表示计算量，路径分析总数越小表示分析计算效率越高。表3为各个方法的传递路径分析计算量，图8所示为输出齿轮的各个方向误差传递路径。

(a)文献[13]方法

(b)文献[4]方法与本文方法图8 输出齿轮误差传递路径Fig.8 The error transfer path of output gear

由图8可以看出，文献[13]的方法基于误差传递路径最短来识别最佳误差传递路径，因此输出齿轮有2条误差传递路径，而本文所述方法与文献[4]得到的结果相同。文献[13]没有考虑零件之间并联结合面的影响，而且在分析过程中只能对单个方向的误差传递路径进行分析。而且对计算工作量(表3)的统计分析发现，对每个方向的误差传递路径分析过程中，需要遍历分析单元中所有的误差传递路径，然后将最短路径作为最佳误差传递路径。对机械系统的误差分析通常是对5个被约束方向的误差的分析，采用文献[13]方法的计算量将非常大。文献[4]和本文的方法可以直接对机械系统中5个被约束方向的误差进行分析，大大减少了计算量。

表3 计算量对比Tab.3 Comparison of calculationburden

本文方法所需分析的路径比文献[4]少，那是因为本文方法在分析时没有对元动作单元中的套筒进行分析。套筒的功能是辅助定位，并没有传递动力，而且仅对输出齿轮产生3个方向的约束。文献[4]的方法没有考虑零件的主要功能，因此需要对所有零件分析，导致分析的路径较多。

5 结语

本文方法从元动作单元的零件功能出发，建立误差传递路径并进行分析，省略了对辅助零件的分析，降低了分析的难度。本文方法可同时对元动作单元等复杂机械系统的5个被约束方向的误差传递路径进行分析，极大地减少工作量，提高分析和计算的效率。

本文方法在分析过程中，对于元动作单元中初步确定的误差传递路径和迭代分析过程中需要添加到误差传递路径中的零件，需要结合经验进行判断分析，初始误差传递路径的选择或添加的零件不合适会增加迭代分析次数，导致计算量变大，计算效率降低。

今后需要在元动作单元零件分类的基础上，对每一类零件的具体功能进行深入分析和研究，确定每一类零件的主要功能和在误差传递过程中的作用，从而在误差分析过程中快速定位并识别主要零件，提高分析的准确性和效率。