温控形状记忆合金的驱动响应模型
2023-02-17鲁友均苗常青
鲁友均 宋 迪,2 苗常青
1.电子科技大学机械与电气工程学院,成都,611731 2.电子科技大学广东电子信息工程研究院,东莞,523808 3.哈尔滨工业大学特种环境复合材料技术国家级重点实验室,哈尔滨,150001
0 引言
形状记忆合金(shape memory alloy,SMA)主要具有两种特殊的力学性能:形状记忆效应和超弹性[1]。目前应用最为广泛的形状记忆合金为近原子比的NiTi形状记忆合金,利用其形状记忆特性可设计出特殊的驱动器。
近年来,形状记忆合金的研究热点主要是:①各种循环加载工况(拉伸、扭转、非比例多轴等)下的材料力学性能,以及根据实验结果建立材料的本构模型;②材料的工业应用。SMA工业应用的快速发展得益于本构关系的不断完善[2],因此,学者从微观、宏观层面提出了描述SMA热机械力学行为的本构模型,其中,微观方法描述材料微观结构的演变[3],宏观方法则基于现象学,考虑实验结果从而得到相应的本构关系。为更准确地刻画奥氏体相与马氏体相之间的作用机制,以及相变过程中的热机械力学行为,将热力学势、内部状态变量和相变硬化函数(指数函数[4]、余弦函数[5]、多项式和光滑函数[6])等逐渐引入本构关系。随后,文献[7-9]对SMA行为模型进行了概述,YU等[10-11]考虑马氏体相变、马氏体重取向、相变诱发塑性、重取向诱发塑性以及它们的交互作用,建立了宏观唯象本构模型和基于物理机理的晶体塑性本构模型。XU等[12]建立的宏观多机制本构模型可描述NiTi形状记忆合金在不同峰值应变下的单程形状记忆效应,且模拟结果较好地描述了单程形状记忆效应的劣化。
SMA本构关系的以上研究提高了对SMA材料性能描述的准确性,推动了SMA驱动器的应用发展。LAGOUDAS[6]通过引入三维本构模型成功设计出航空发动机外涵喷口降噪智能结构和医用SMA血管支架,SAPUTO等[13]对SMA驱动器的设计进行了详细总结,并对驱动过程进行了数值模拟。WEIRICH等[14]验证了SMA驱动器在航空航天领域应用的可能。SMA驱动器的类别、辅助机构形式、驱动热源类型对驱动性能都有直接影响。航空航天领域中,SMA驱动器可用于可变形机翼驱动装置、太阳能电池板展开装置驱动器、卫星折展天线、锁紧释放装置等。上述应用依赖形状记忆合金材料的性能发挥,因此,找到一种较为便捷且准确的驱动响应分析方法是近一步推动SMA驱动器应用的关键。
本文首先基于热传导方程与驱动几何关系,建立温控SMA驱动器的驱动响应模型[15],通过马氏体体积分数修正模型中的电阻、弹性模量、剪切模量等参数,以提高驱动响应模型的准确性。其次,引入截面平均应变,确立了不同截面形状对驱动响应速度的影响规律。理论分析了温控SMA丝状驱动器在驱动过程中的圆心角和弯矩响应。搭建了实验平台,测试了直径为1.2 mm、长度为10π mm、初始圆心角为30°的SMA丝在6A电流下的驱动响应情况,并将其与本文建立的温控SMA驱动响应模型计算结果进行对比分析。
1 温控SMA驱动器的建模分析
SMA驱动器是利用SMA的形状记忆效应在形状恢复中产生驱动力,达到驱动效果的结构或单元[16]。形状记忆效应是指材料在外界环境(一般是温度)发生变化时,内部发生的热弹性马氏体相变引起的宏观响应,具体表现为SMA材料恢复到原始状态的形状。形状记忆效应机制如图1所示。

图1 形状记忆合金的形状记忆效应机制Fig.1 Shape memory mechanism of SMA
SMA根据其驱动和回复的性能,主要分成单程SMA、双程SMA、全程SMA,相应的驱动方式和过程如图2所示[17]。

图2 SMA驱动器宏观驱动过程[17]Fig.2 SMA drive macro drive process
单程SMA的性能比较稳定,工程应用广泛。若要单程SMA驱动器实现往返动作,则需将单程SMA驱动器与偏置机构或差动机构配合,利用偏置机构或差动机构的回复力完成驱动之后的回复动作。如图3a所示,初始状态时,将有残余应变的SMA丝一端与偏置弹簧(此时没有拉伸或压缩)连接;SMA丝加热后收缩,驱动点向上运动,产生的驱动力使偏置弹簧处于拉伸状态;冷却后,单程SMA丝不会自动回到原始位置,驱动力消失,而收缩的偏置弹簧可使SMA丝回复到加热前的长度,并使驱动点回到原来位置。通过类似的原理可将偏置弹簧设计成SMA弹簧,如图3b所示,驱动器采用差动结构,加热2个SMA弹簧使其收缩,实现不同方向的驱动并使弹簧恢复到原始位置。如先对弹簧a加热使其收缩,提供向上的驱动力;弹簧a停止加热后,再对弹簧b加热使其收缩,以使驱动点回到原来位置,并提供向下的驱动力。

(a)偏置式 (b)差动式图3 单程SMA驱动器典型应用Fig.3 Typical application of one-way SMA actuator
SMA驱动器建模分析前,需要对实际场景进行简化。具体的简化说明如下:
(1)驱动器的加热方式为电流加热。
(2)假定温度的变化与驱动同时进行,即驱动单元温度达到开始温度Ts时逆相变开始发生,驱动动作开始;温度达到结束温度Tf时逆相变结束。
(3)驱动单元形状的变化是连续的,不会产生突变。
(4)动作温度不高且辐射面积小,因此热辐射导致的温度损耗可以忽略。
(5)驱动器电流流入端的加热时间长于流出端的加热时间,导致流入端的温度高于流出端的温度即产生温度梯度。温度梯度导致晶粒尺寸存在梯度效应,进而对材料的力学性能产生一定的影响[18],如材料两端温度的不同导致弹性模量不一致。温度梯度的影响区域虽然比较小,但分析微尺寸SMA驱动器的驱动响应时不能忽略该影响因素。
(6)驱动过程中,驱动器结构处于平衡状态。
有效接入电路部分的SMA丝为驱动单元,对应的热力学方程如下:
Qradiation+Qconvention+Qtransfer=Qinput
(1)
Qinput=I2Rt
(2)
Qconvention=hcA(Tw-T0)
(3)
Qtransfer=cmΔT
(4)
(5)
式中,σa、εa分别为表面发射率和辐射常数;c、m分别为SMA的比热容和质量;hc、A、Tw、T0分别为对流传热系数、表面积、SMA弹簧的温度和环境(此处为空气)的温度。
实际驱动时,热辐射的占比很小且工作温度较低,因此,本小节将热辐射忽略。再将过程公式等号两端都对时间t进行微分,得到加热过程的方程:
(6)
式中,ρ为材料密度;V为材料体积。
整理式(6),求解一元微分方程,得材料温度T随参数变化的响应公式:
(7)
式中,C1为求解一元微分方程后的常数,由初始条件决定。
为便于直观观察响应,选择圆心角为响应变量,将SMA驱动器的自由恢复过程简化。如图4所示,驱动单元在低温时受到外力发生变形即C-A-B状态;对弯曲段AB加热,材料发生马氏体逆相变,宏观上表现为材料恢复到受力变形前的形状即C-A-B′状态。驱动过程是材料弯曲段AB受热发生马氏体逆相变,恢复成直线AB′,假定在驱动过程中AB变化是连续的,且驱动过程中的角度关系为

图4 SMA丝驱动过程示意图Fig.4 Schematic diagram of SMA wire actuating process
β=θ
(8)
驱动过程中,假定中性轴的长度不发生变化即AB弧长不变,根据弧长公式,可以得到
L=R0θ0=Riθi
(9)
式中,R0、θ0分别初始状态的曲率半径与圆心角;Ri、θi分别为驱动过程中任意位置的曲率半径和圆心角。
根据几何关系可得曲率的表达式[19]:
(10)
L1=L(1+ε1)L2=L(1+ε2)
式中,r为截面内接圆的半径;ε1、εp1分别为受拉侧初始状态的平均应变和平均塑性应变;ε2、εp2分别为受压侧初始状态的平均应变和平均塑性应变。
圆心角θi与应变之间的关系为
(11)
SMA升温后形状恢复的根本原因是温度诱发SMA热弹性马氏体逆相变(宏观上表现为形状恢复)。笔者认为存在驱动响应的开始温度Ts和结束温度Tf,则在材料整体的升温过程中,圆心角响应为
(12)
(13)
(14)
材料的最大应变发生在截面的最外侧和最内侧,通过截面应变原理得到截面产生的最大应变
(15)
本文中的SMA驱动器截面形状是关于中性层对称的正多边形,因此可将应变的分布简化成对称分布,且应变大小与该点到中性层的距离成正比[20]。将截面受拉侧的应变定义为正,受压侧截面的应变定义为负,故截面任意材料点的应变为
εi=y/R0
(16)
由此可以得到截面上任意位置处的应变,从而计算得到截面上的平均应变
(17)
式中,H1表示截面受拉区域;SH1为受拉侧的面积。
同理可得受压侧产生的平均应变
(18)
式中,H2表示截面受压区域;SH2为受压侧的面积。
在式(12)~式(14)的计算中使用截面平均应变代替截面最大应变更能体现截面形状对应变分布和驱动响应的影响。
将式(13)、式(14)、式(17)、式(18)代入式(12)即可得到驱动过程的圆心角。根据驱动器曲率与弯矩的关系[21],可得
(19)
进而得到弯矩
(20)
式中,Ei为驱动过程中材料的弹性模量;ISMA为SMA驱动器截面中性轴的惯性矩。
驱动过程中,弹性模量随着马氏体逆相变的发生而变化,而马氏体的逆相变发生程度又与温度有关,于是弹性模量可写成
(21)
式中,EA、EM分别为奥氏体状态下和马氏体状态下的弹性模量。
以上为一个弯曲单元响应的推导,实际驱动过程中,驱动器由多个驱动单元叠加而成,变形较为复杂,因此,若要分析复杂驱动器的响应,可以先将其分为多个弯曲单元,先分别分析驱动响应,再将各单元响应进行运动学叠加。
2 截面形状影响研究及算例分析
研究中的截面形状关于中性层对称,但实际应用中的截面形状多种多样,本文通过增加内接多边形的边数来构造不同截面形状的SMA驱动器,常见的截面形状如图5所示。

图5 常见规则截面形状Fig.5 Common regular cross-sectional shapes
现有的SMA丝自由恢复响应研究中,考虑截面形状对响应情况影响的研究较少。本节首先通过前文提出的方法对不同截面形状的平均应变进行分析计算。计算过程中,为简化计算的流程,将不同截面形状的驱动器质量m、电阻Ri、热流面积A统一表达为
(22)
(23)
(24)
式中,n、L分别为截面正多边形的边数和SMA丝驱动器的长度。
为便于后期实验观测,SMA驱动器的初始尺寸设置相同,即驱动单元截面外接圆直径为1.2 mm,长度为10π mm,初始圆心角为30°。截面上产生最大应变的位置为截面上离中性层最远的点。计算可得不同截面形状的平均应变,如表1所示。

表1 不同截面形状平均应变情况Tab.1 Average strain of different cross-sectional shapes
将电流6A代入温度响应模型可得温度变化值,将温度变化值和不同截面形状的平均应变代入圆心角响应模型可得SMA驱动器圆心角的变化,如图6所示。

图6 不同截面圆心角响应情况Fig.6 Response of central angle of different sections
由表1和图6可知,随着边数的增加,平均应变增加速率逐渐降低,平均应变趋于稳定,并且驱动器响应过程的差别也逐渐减小,因此,当边数大于8时,截面的形状对驱动过程的响应影响不明显。由图6可以看出,截面边数增加时,响应将会变慢,因此,在其他条件满足的情况下,减少材料截面边数有利于提高响应速度。
响应速度的直接决定因素是驱动器自身温度变化的速率,温度变化速率取决于材料电阻,而驱动器的电阻取决于截面积、电阻率、驱动单元长度。本节中,驱动单元长度是固定不变的,SMA的电阻率随马氏体含量的降低而减小,因此,可以看到随着驱动时间的延长,角度变化逐渐变慢。截面形状是正多边形且具有相同的外接圆,因此,随着边数的增加,其面积将会收敛,进而导致响应速度收敛。因此,要提高响应速度,可以在满足功能要求的情况下减小截面边数,进而增大电阻,达到提高响应速度的目的。值得注意的是,本文的研究工作只涉及一个驱动单元,若驱动器由多个单元组成,则将各个驱动单元的响应进行运动学叠加,从而得到整个驱动器的响应。
工程上最常见的截面形状是圆形和方形。基于本文的建模分析方法,将材料参数代入响应方程,对这两种截面形状的SMA驱动器升温自由恢复过程的驱动响应进行数值模拟。初始状态下,SMA驱动器受外载荷作用而变形,弯曲部分截面上的应变可简化成线性分布[18],如图7所示。

(a)方形截面在初始外载荷下变形 (b)方形截面应变分布
(c)圆形截面在初始外载荷下变形 (d)圆形截面应变分布图7 初始外载荷下截面的变形和应变分布Fig.7 Deformation and strain distribution of cross-sections with initial external load
将截面形状特征代入应变表达式,得到方形截面的平均应变
(25)
和圆形截面的平均应变
(26)
式中,下标f表示方形截面;下标y表示圆形截面。
值得注意的是,本算例分析中截面外接圆直径为1.2 mm,长度为10π mm,初始圆心角为30°,驱动电流为6 A,将材料参数代入式(6),计算得到温度变化,绘制温度响应曲线,如图8所示。

图8 截面的温度响应Fig.8 Temperature response of cross-sections
将上述随时间变化的温度响应值和材料参数代入式(12)~式(14),得到温升过程中的圆心角响应情况,如图9所示。

图9 截面的圆心角响应Fig.9 Central angle response of cross-sections
将式(25)、式(26)分别代入式(20),得到截面弯矩的变化,绘制弯矩响应曲线,如图10所示。本文中的材料参数如表2所示。

图10 截面的弯矩响应Fig.10 Bending moment response of cross-sections

表2 材料参数Tab.2 Material parameters
3 温控SMA丝弯曲驱动性能测试
本文所采用的材料是江阴法尔胜佩尔新材料科技有限公司提供的直径1.2 mm的黑面态形状记忆合金丝。为研究该材料的驱动响应需在常温下先施加外力、产生预变形,任初始状态和算例分析初始情况一致。
首先截取110 mm的驱动丝,随后在中间连接导线,导线有效作用长度是10π mm。驱动丝通过外力预处理成半径60 mm、圆心角30°的圆弧。
夹头与驱动丝由铜线连接以减小外载荷对驱动过程的影响。驱动过程中,采用摄像机拍摄SMA丝驱动过程,部分视频截图见图11。

图11 不同时刻驱动响应Fig.11 Drive response at different times
驱动丝中间没有安装固定装置,因此,驱动过程中,驱动丝与纸面的摩擦力会对展开过程驱动丝的位置和形态产生一定程度的影响,导致两辅助垂线不具有与初始位置一样的完全对称分布,但该影响较小,可以忽略。10 s、12 s、14 s的辅助垂线在图像窗口外,故通过做辅助线来获取角度,图中虚线平行于下方的垂线。
由图12可以看出,理论值与实验值的趋势相同,但引入动态修正能明显提高模型的准确性。实验响应曲线存在滞后,其产生原因有:①与驱动丝相连接的铜线质量对驱动丝角度的变化有一定程度的阻碍作用;②形状记忆合金材料的温度滞后特性。
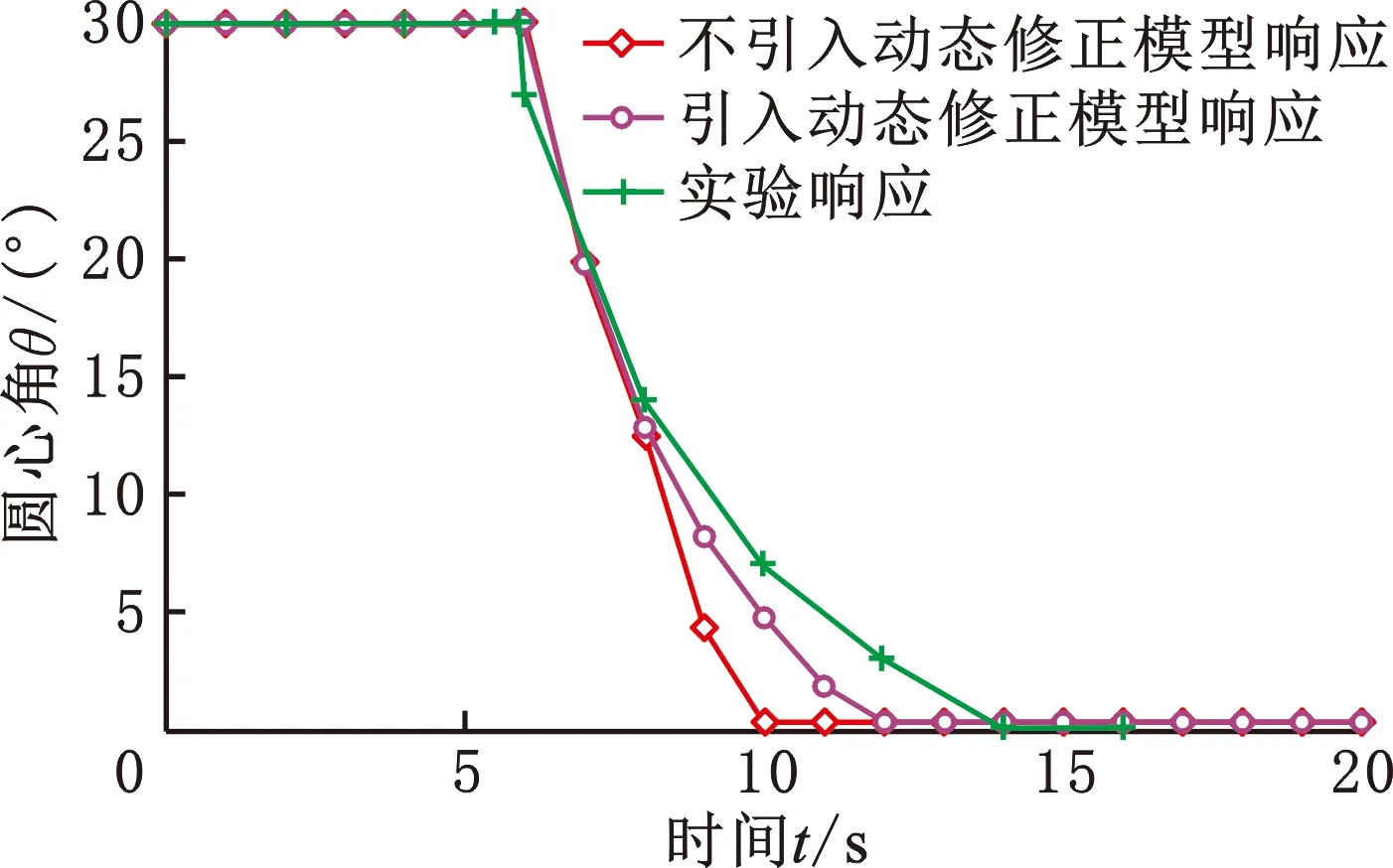
图12 驱动响应的实验结果与模型计算结果Fig.12 Test results and model calculation results of actuating response
4 结论
(1)基于传热学的经典能量方程与驱动几何关系,建立了温控形状记忆合金驱动器的驱动响应模型。该模型通过线性化处理温升过程中材料的马氏体体积分数来动态修正形状记忆合金的电阻、弹性模量等受温度影响的参数,并将修正前后的驱动响应模型数据与实际角度驱动实验的数据绘图进行比较。研究发现,角度完全恢复时的时间误差最大;最大时间误差由未引入动态修正模型的3.8s降低至引入动态修正后的1.8 s,提高了模型的精度。
(2)分析了截面形状对驱动响应的影响。本文采用的截面平均应变可以更加准确地描述整个截面的应变。截面边数小于8时,通过减小边数可以提高响应速度;边数大于8时,截面形状对响应速度的影响较小。
(3)本文搭建了温控SMA丝弯曲驱动性能测试实验平台,基于该平台测试了6A电流驱动下,直径1.2 mm、长度10π mm、初始圆心角30°的温控SMA丝圆心角响应,响应模型可较为准确地对驱动过程进行描述。
后续将继续深入研究如下问题:①温度梯度对微尺寸驱动器的影响;②采用基于热力学的本构模型描述马氏体的体积分数,获得更加精准的结果;③截面形状与驱动行为的关系;④驱动器有负载或者负载不可忽略时,需要引入平衡方程,获得结构整体的响应情况。
