海底控制点水声定位测距误差的近似数学表达式

孙文舟，曾安敏，乔正明，赵 翔

(1.地理信息工程国家重点实验室，西安 710054；2.国家海洋技术中心漳州基地筹建办公室，厦门 361007)

GNSS 结合声学设备是实现绝对基准向海底控制点传递的最有效方法[1-4]，影响该方法测量准确性最大的误差源是声速的不确定性[5]，声速的误差由测量的不准确、温度的日变化以及内波等因素引起[6,7]。由于斜距值(即海底应答器至船底换能器直线距离)的计算方法复杂，且计算时需要以声速剖面而非单一声速值为基础量，因此，声速的不确定性引起的测距误差规律难以把握，还没有形成确定性的解释[1]。

文献[8]利用圆走航确定水下控制点的三维坐标，认为当水深一定，船底换能器与海底应答器水平距离相等时，声速误差近似为常量；文献[9]认为声速误差与声传播时间和声波垂直发射到达海底应答器时间之差的平方具有线性关系，其中，两者伪距的计算都是采用某一代表性声速与声传播时间的乘积。文献[10]开展的实测试验表明，当声速剖面存在某一固定偏差时，测距误差与斜距值线性负相关，但具体原因仍未知。

为了解声速不确定性引起测距误差的变化规律，本文尝试基于声速剖面和传播时间的线性关系理论（The linear relationship between sound velocity profile area and propagation time，简称“ST 定理”）对其进行推导分析[11]，建立测距误差的数学模型，为海底控制点测定的测线布设，解算模型优化提供相关依据。

1 控制点定位测距误差分析

分析控制点定位测距误差必须基于水下斜距值特有的计算方法，与陆地上斜距值的确定方法不同，船底换能器到海底应答器斜距值的计算不能直接采用某一代表性声速与传播时间的乘积，而应基于声线跟踪的原理计算，但由于初始入射角是未知数，因此采用迭代的方法来求初始入射角，进而得到所需的斜距值[12]，迭代计算初始入射角具体的计算原理可参考文献[12]，若参考深度、声速剖面和传播时间等观测量均不包含误差，则由算法本身引起的测距误差是可以忽略的，本文提出的测距误差表达式主要针对由声速不确定性引起的测距误差，结合图1来对这项误差进行分析。

图1 中，O点为声源位置，P点为海底应答器真实位置，在参考深度和声速剖面精确已知的情况下，从O点开始，采用声线跟踪法经过实测传播时间t声线脚印位置将到达P。若声速剖面的测量不准确或由于在时间上的变化造成扰动，则实际的声线脚印位置可能落在P1或者P2。而在准确的声速剖面下，声线从O点到P1点经历的传播时间必然小于t，设差值为dt1，同理，声线从O点到P2点经历的传播时间必然大于t，设差值为dt2。显然dt1、dt2相比于t是极小的，进而认为角度δθ也是极小的，所以由声速的不准确引起的测距误差可表示为时间差与海底声速cb的乘积，表示为：

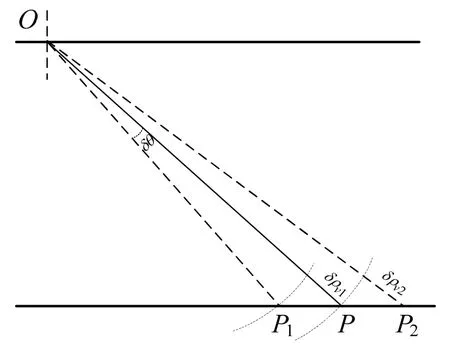
图1 测距误差分析示意图Fig.1 Schematic diagram of ranging error analysis

2 测距误差的近似数学表达式

测距误差表达式的推导基于ST 定理[11]，ST 定理描述了传播时间与声速剖面的关系，定义为当船底换能器与海底应答器的相对位置恒定时，在某一有限的声速变化范围内，声传播时间与声速剖面面积线性法负相关，表示为：

也可写为：

式中，T0是背景声速剖面下声波从声源传播至海底应答器经历的时间，T是瞬时声速剖面下声波从声源传播至海底应答器经历的时间，S0是背景声速剖面相对于z轴围成的面积[11]，如图2 中蓝色阴影部分所示，S是瞬时声速剖面相对于z轴围成的面积，如图2 中红色阴影部分所示，k0=T0/S0是与初始入射角有关的系数，Δs=S－S0是声速剖面面积在背景声速剖面面积上的变化量，Δt=T－T0。

图2 声速剖面面积示意图Fig.2 Schematic diagram of sound velocity profile area

根据ST 定理的描述，测时误差可进一步表示为：

式中，ΔS是实际声速剖面与用于计算声速剖面的面积差，k0可用下式表示：

式中，ρ是应答器到换能器的斜距值，ce是有效声速值，为斜距值与实际传播时间之比，随初始入射角而变化。将式(5)和式(4)代入式(1)可得：

有效声速ce是随入射角变化的变量，为简化表达式，用常量harmonic 平均声速ch替换有效声速ce可得[13]：

上式即为测距误差的数学表达式。根据定义可知ch和ce在初始入射角为0 时相等，初始入射角越大偏差越大，定义相对声速误差为：

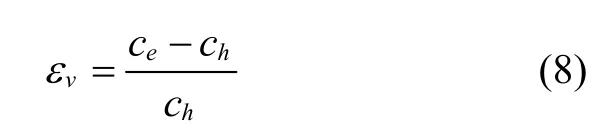
定义由于ch替换ce所引起的相对测距误差为：

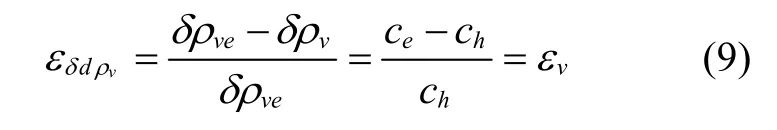
由式(9)可知相对声速误差与相对测距误差相等，因此当初始入射角越大时，相对测距误差越大，即测距误差表达式的估值与真实值的偏差越大。

3 仿真试验分析

本文设计如下仿真试验验证表达式的有效性，坐标系选用笛卡尔坐标系，坐标原点为海底应答器的位置，x轴指向东，y轴指向北，z轴指向天顶，水深3000 m，测量船航速为3 m/s，每20 秒采样一次，从应答器正上方海面开始做远离该点的直线运动。

试验中的声速剖面包括时变部分和非时变部分，非时变部分由Munk 标准方程构建[14]：

式中，C1=1482 m/s 是声道轴处的声速，Z1=1000 m 是声道轴的深度，ε=7.4×10-3是扰动系数，B=1300 是声道尺度厚度，仿真得到背景声速剖面如图3 所示。

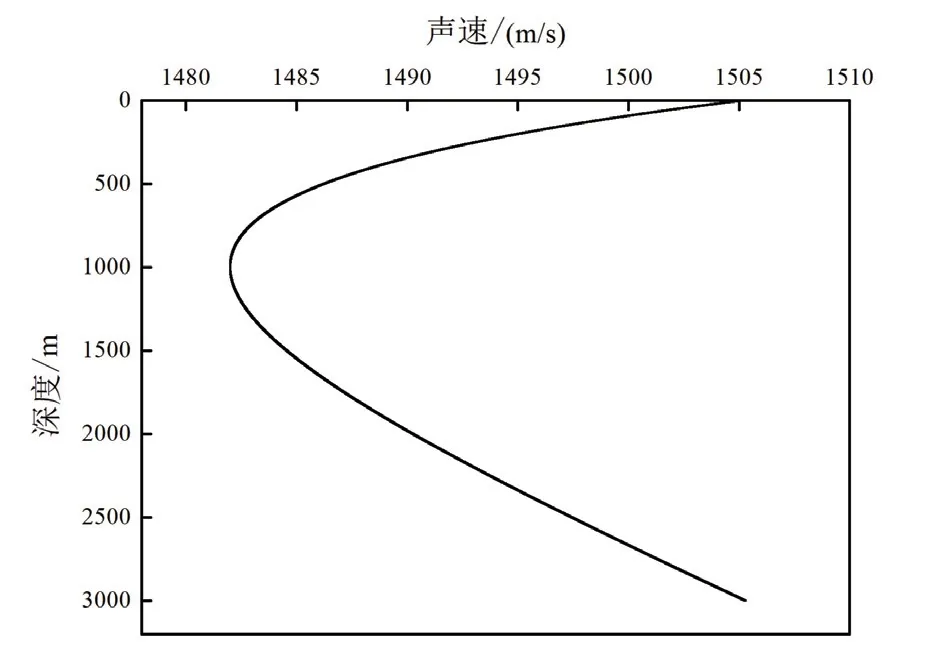
图3 背景声速剖面Fig.3 Background sound velocity profile

声速剖面的时变部分包括温度日变化引起的长周期项和内波等引起的短周期项，根据文献[15]的方法进行仿真得到，如图4-5 所示。

图4 温度日变化引起的声速剖面变化Fig.4 Variation of sound velocity profile caused by diurnal temperature variation

因为船底换能器和海底应答器的相对位置已知，同时任意时刻的声速剖面可以通过在背景声速剖面上迭加长周期项和短周期项得到，基于常梯度声线跟踪法可计算观测量传播时间，方法是不断调整初始入射角，当声线脚印位置与应答器位置之间的距离小于某一限差时，对应的传播时间为所求值[16]。实际斜距值基于此观测量、应答器参考深度以及某一固定声速剖面（本文选用背景声速剖面），根据文献[12]的方法迭代计算获得。计算得到的斜距值减去斜距值真值即是测距误差真值。最后用式(7)估计测距误差，得到的结果如图6 所示，图7 是斜距值与初始入射角的对应关系。

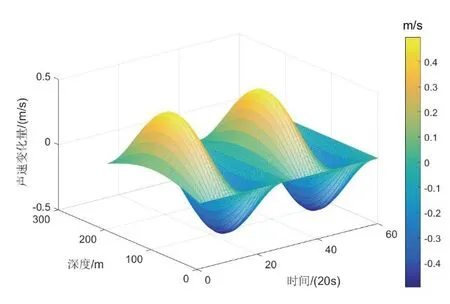
图5 内波引起的声速剖面变化Fig.5 Variation of sound velocity profile caused by internal waves

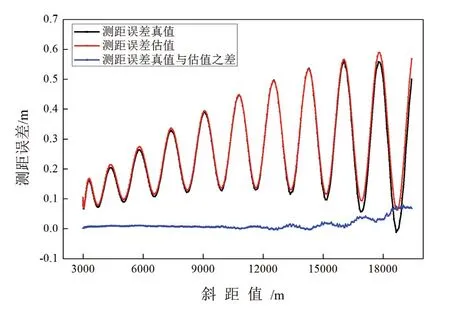
图6 测距误差估计值与真实值对比Fig.6 Comparison of estimated and true range error values

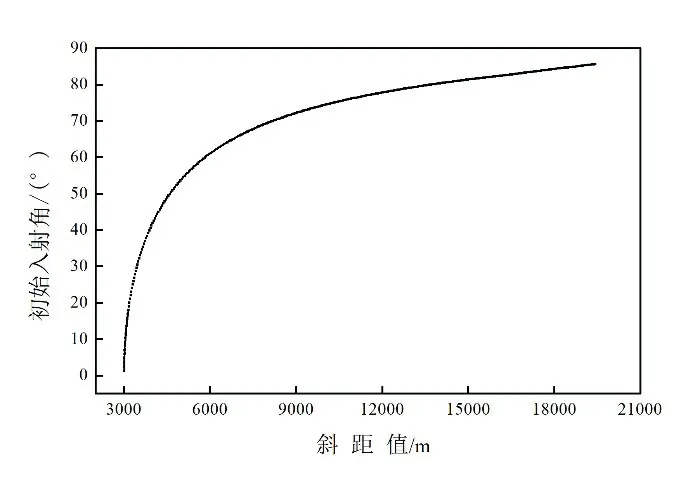
图7 斜距值与初始入射角对应关系Fig.7 The corresponding relationship between the slant range and the initial incident angle

图6 中的黑色实线是仿真试验得到的测距误差真值，红色实线是根据式(7)估算的测距误差，蓝色实线是测距误差真值与估值之差，可以看出估值绝对误差的趋势随斜距值增大而上升。在斜距值为15000 m(初始入射角约80 °)以内估值的绝对误差在1 cm 以内，当斜距值增大至18000 m 左右时(初始入射角约86 °)估值出现约7 cm 的绝对误差，证明了该表达式可以对测距误差进行有效的描述。图中测距误差明显的周期性变化规律是由仿真试验设置的内波和温度日变化条件引起的声速剖面变化导致。

图8是harmonic平均声速ch和有效声速ce之差，差值随斜距值的增大而增大，由前文分析可知这是造成测距误差表达式估值的绝对误差增大的主要原因。

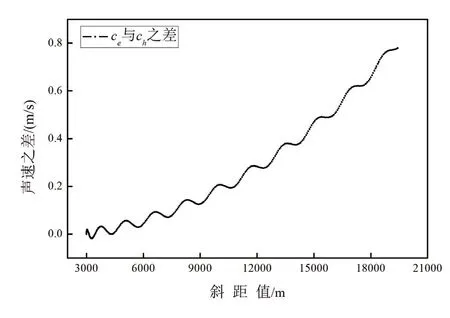
图8 ce 和ch 之差Fig.8 The difference between ce and ch

总体而言，该试验验证了本文提出的测距误差表达式的准确性，尤其初始入射角在80°以内情况下，具有较高的准确性。

4 结论

本文基于ST 定理推导了海底控制点坐标测定问题中，声速不确定性引起测距误差的数学表达式，结合仿真试验分析得出了如下结论；

1）测距误差可以近似用式(7)表示，且该式中仅有两个是变量，声速剖面面积差和应答器到换能器的斜距值。

2）测距误差与声速剖面面积差和斜距值都是线性负相关的关系，声速剖面面积差具有时变性，若忽略内波，温度日变化等因素对声速剖面的影响，可认为声速剖面面积差为常量，此时测距误差仅与斜距值有关。

3）测距误差随初始入射角增大而增加，因此在进行海底控制点坐标测定的作业时，应尽量避免初始入射角过大。

本文提出的数学表达式描述了声速不确定性引起测距误差的规律，可用于声学测距声速误差模型的建立，对解决水下静态目标定位以及水下载体动态导航定位中的声速误差修正问题有一定帮助。