联合低秩张量分解与稀疏表示的高光谱异常目标检测算法

成宝芝， 张丽丽， 赵春晖

(1.常州工学院计算机信息工程学院，江苏 常州 213000； 2.大庆师范学院机电工程学院，黑龙江 大庆 163000；3.哈尔滨工程大学信息与通信工程学院，哈尔滨 150000)

0 引言

高光谱是由二维的空间谱和一维的光谱构成的>“图谱合一”的遥感图像，高光谱图像通过极高的光谱分辨率能够对存在光谱差异的不同地物进行识别[1]。近年来，高光谱图像在光谱解混、分类和目标检测等方面得到大量应用,其中，对不需要任何先验信息的异常目标检测的研究及其应用成为一个研究热点。从背景区域将异常目标检测和识别出来，主要是根据两个原则：一是异常目标的光谱特性明显偏离其邻域光谱；二是异常目标在整个图像中是一个小概率发生事件，即异常目标存在稀疏特性[2]。高光谱异常目标检测在军事和民用等领域都有广泛的应用，比如海上溢油检测、战场目标的准确识别以及农产品的质量检验等[3]。

总的来说，高光谱图像异常目标检测算法的研究主要分为基于统计的方法和基于表示的方法[4]。文献[5]提出的RX异常检测方法，是基于统计的异常检测算法中的经典方法,该方法简化了高斯多元分布的背景模型，通过异常目标不同于背景特征分布这一高光谱图像特性，利用马氏距离进行异常目标检测。 由于高光谱图像分布的复杂性，背景分布往往偏离高斯分布，因此，传统的RX异常检测算子方法检测精度偏低。其他研究者对经典的RX异常检测方法进行改进，先后提出快速RX检测[6]、全局RX[7]、RX-UTD[8]、加权RX[9]，local RX detector (LRXD)[10]等，这些算法都从不同角度对经典的RX异常检测方法进行改进，提高了基于RX异常检测算子检测方法的有效性和鲁棒性。

近年来，基于表示的高光谱异常检测方法得到越来越多的重视。文献[11]将稀疏表示引入高光谱异常检测中，通过光谱稀疏差异指数和空间稀疏差异指数进行加权，得到异常目标判决公式进而判断检测对象是异常目标还是背景，该方法得到了较好的异常检测结果。联合低秩矩阵和稀疏矩阵分解(Low-Rank and Sparse Matrix Decomposition,LRaSMD)进行异常检测的方法成为近期的研究热点[12-13]，该方法的主要思想是：高光谱图像是由背景、异常目标和噪声组成。一方面，由于高光谱图像是由光谱和空间谱组成的三维图像数据，背景包含了主要信息内容，而且数百个光谱带具有互相关和均匀区域，因此，背景可以假定为低秩矩阵。另一方面，与背景信息相比，异常目标样本较少，被认为是稀疏的。高光谱图像中的噪声基本上由条纹噪声、高斯白噪声和光电噪声组成，通常可以模型化为独立分布的高斯随机变量[14]。文献[15]提出的LSDM-MoG异常检测方法，用混合高斯分布代替单一分布，从而能够更好地检测和识别异常与不同类型的噪声；文献[16]提出的OSP-LRaSMD 异常检测方法，将稀疏分量投影到背景正交子空间，由低秩分量估计背景正交子空间，从而抑制背景干扰、突出异常目标。

本文通过对低秩矩阵联合稀疏表示方法的分析和研究，提出了联合低秩张量分解与稀疏表示(Low-Rank Tensor Decomposition and Sparse Representation，LRTD-SR)的高光谱异常目标检测算法，该算法首先利用低秩张量分解方法进行高光谱图像数据恢复，使得高光谱图像质量得到提升，异常目标信息能够更容易被检测到。在此基础上，引入稀疏表示方法，利用稀疏差异指数进行异常检测处理，得到异常目标检测结果。

1 方法

1.1 张量分解理论

高光谱图像为空间谱和光谱构成的三维谱。因此，高光谱图像可以利用张量进行表示和分解，如图1所示，其中，1-mode和2-mode表示空间维，3-mode表示光谱维。

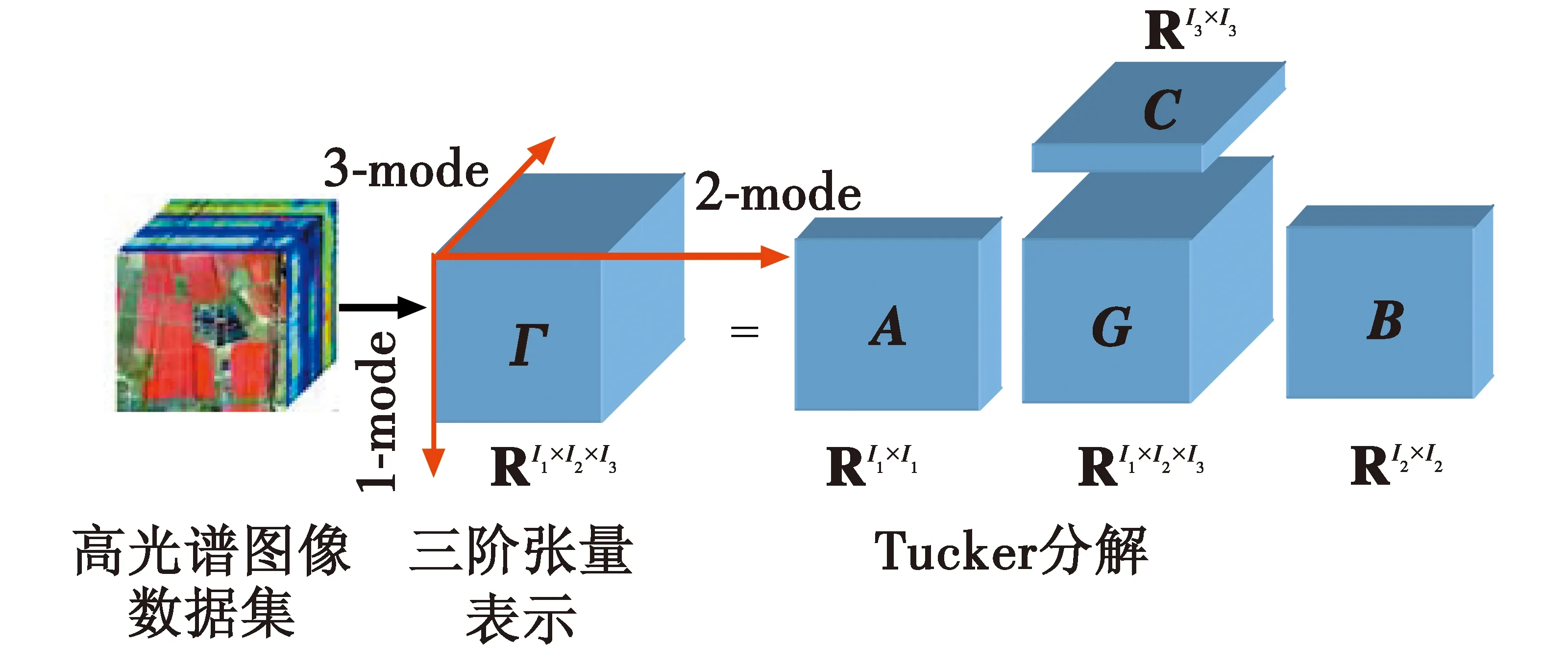
图1 高光谱数据张量表示和分解Fig.1 Tensor representation and decomposition of hyperspectral data

首先，假设Γ∈RI1×I2×I3为一个潜在干净的高光谱数据，其中，I1×I2为空间谱的长和宽，I3为光谱维的维数。然后，利用Tucker进行张量分解，核张量表示为

Γ=G×1A×2B×3C

(1)

式中：G=RJ1×J2×J3，为核心矩阵；A∈RI1×J1，B∈RI2×J2和C∈RI3×J3是分解之后得到的因子矩阵。

gj1j2j3作为G的元素，表示不同成分之间的互连程度，由此，式(1)可以分解为

(2)

式中：τi1i2i3为Γ的元素；J1，J2和J3分别为张量分解后A，B和C的成分数目；ai1j1，bi2j2，ci3j3分别为A，B和C的元素。

为了得到G，式(1)分解优化为

(3)

s.t.G∈RJ1×J2×J3，A∈RI1×J1,B∈RI2×J2,C∈RI3×J3，ATA=I,BTB=I,CTC=I

因为A，B和C有正交列，G=Γ×1AT×2BT×3CT可以从式(3)中求得，I为单位矩阵。式(3)的最小化问题等于如下的最大化问题，即

(4)

s.t.A∈RI1×J1,B∈RI2×J2,C∈RI3×J3，ATA=I,BTB=I,CTC=I。

1.2 低秩矩阵恢复模型

低秩矩阵恢复模型(Low-Rank Matrix Recovery Model,LRMRM)[17]被引入图像处理中，用于处理数据低秩性恢复问题。给定一组图像数据样本，LRMRM的目标是联合寻找所有数据的最低秩表示，该模型在低维子空间数据处理方面非常有效。

假设γ∈Rm×n为一个含有噪声的图像数据，可表示为

γ=H+L

(5)

式中：H为低秩矩阵；L为稀疏误差矩阵。

为了得到H，可以将式(5)转化为松弛的凸优化问题，即

minH,L‖H‖*+η‖L‖1

(6)

s.t.γ=H+L

式中：‖H‖*表示核范数；η为正则化参数，用于平衡核范数和L1范数之间的相对比例。

对于式(6)的求解，核心目的是得到恢复之后的H，采用的方法为增广拉格朗日乘子算法，即交替方向方法(Alternating Direction Methods,ADM)。

通过对高光谱图像数据进行分析，低秩矩阵恢复模型实现了高光谱波段的矢量化，但是，高光谱图像波段间的相关性受到破坏。因此，基于高光谱图像的三维数据结构，采用张量结合低秩矩阵方法进行高光谱数据处理，能够保持高光谱图像波段间的空间结构和光谱特性的细节，使得数据处理结果更加精确[18]。通过低秩张量分解之后的高光谱图像数据，再利用稀疏差异指数方法进行异常目标检测。由于原始高光谱图像受高光谱传感器、噪声、水汽等影响，使得图像数据产生降质。采用合适的方法对原始高光谱图像数据质量进行恢复，再进行异常目标检测，是一类具有创新性的方法。因此，高光谱图像数据恢复技术的采用非常重要，对比现有的高光谱图像数据恢复方法，采用文献[18]提出的加权群稀疏正则化低秩张量分解(LRTDGS)方法进行图像数据恢复。

假定高光谱图像数据为

Y=Γ+S+E

(7)

式中：Y为含有噪声的高光谱图像；Γ为潜在干净的高光谱图像；S为除了高斯噪声之外的其他噪声构成的稀疏噪声；E为高斯噪声。

由此，LRTDGS模型表示为

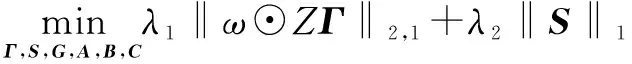
(8)

s.t.Γ=G×1A×2B×3C‖Y-Γ-S‖2≤ε

式中：λ1和λ2为正则化参数；ω为非负加权变量；Z为空间维度上的微分算子；ε为高斯噪声密度方差。在LRTDGS模型中，充分利用了潜在干净的高光谱图像(数据集)Γ和稀疏噪声S的先验知识，同时，低秩张量Tucker分解能够保持空间和光谱的相关性，并利用加权群稀疏约束来保持所有波段的共享局部平滑度。

1.3 稀疏分解表示及差异指数

经过低秩张量模型处理过的高光谱图像数据集Y′利用稀疏分解表示方法进行处理，得到需要的异常目标检测结果。Y′表示为

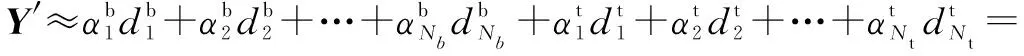
(9)

式中：D为ћ×(Nb+Nt)矩阵，是由背景Db和异常目标Dt构成的字典空间(Db和Dt分别是背景子字典矩阵和目标子字典矩阵)；ћ表示高光谱图像的波段数，Nb为背景的像元数，Nt为目标的像元数；α=αb+αt，为稀疏系数权向量(αb和αt分别为背景系数权向量和目标系数权向量)。

通过α的结果判断被检测的像元是背景还是目标，因此，α的最优化问题可以表示为

α=arg min‖α‖1

(10)

s.t.Dα=Y′。

该最优化问题利用稀疏差异指数[11]完成异常检测。假设α*为权向量，N为权向量α*的维数，则光谱稀疏差异指数为

(11)

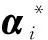
第j个波段的空间稀疏差异指数为

(12)

(13)

式中，Λ为波段总数。

通过将光谱稀疏差异指数和空间稀疏差异指数协同处理高光谱图像，能够从高光谱图像背景信息中得到不同于背景信息分布的异常目标像元，从而检测出异常目标，得到高光谱图像处理要求的结果。

1.4 算法实现步骤

LRTD-SR算法利用低秩张量进行高光谱图像恢复，经过低秩矩阵恢复模型LRTDGS方法处理后的高光谱图像，再利用稀疏差异指数进行异常目标检测，从而得到异常检测结果。具体步骤如下：

1) 输入待检测的高光谱图像数据集；

2) 利用基于低秩张量分解的LRTDGS方法模型对原始的高光谱图像进行图像数据恢复，得到恢复之后的高光谱图像；

3) 引入稀疏分解理论，利用稀疏差异指数对恢复后的高光谱图像进行异常目标检测；

4) 输出高光谱图像异常目标检测结果，利用二值图像表示背景和异常信息。

2 仿真实验和结果分析

2.1 真实高光谱图像数据

为了验证LRTD-SR算法的异常检测性能，利用真实的高光谱图像进行仿真实验并对检测结果进行分析。圣地亚哥海军机场高光谱遥感图像被广泛用于异常目标检测，该图像来自于机载可见光/红外成像光谱仪(Airborne Visible/Infrared Imaging Spectrometer，AVIRIS)，最初的波段数为224个，去除掉污染严重的波段后剩余126个，空间分辨率为3.5 m，大小为400像元×400像元。仿真实验中截取的图像大小为100像元×100像元×126像元，含有38个异常目标。如图2所示。

图2 仿真用的高光谱图像Fig.2 The hyperspectral imagery for simulation

2.2 仿真过程及结果分析

为了验证本文所提LRTD-SR算法的检测率和鲁棒性，同时仿真了LRTVTD-SR算法[19]、LSD算法[11]、KRX算法和经典的RX算法。LRTVTD-SR算法是先利用总变分正则化低秩张量方法对原始高光谱图像进行图像提质，然后利用稀疏表示方法进行异常检测；LSD算法是一类基于稀疏表示的异常目标检测方法；KRX算法是一类非线性核函数RX异常目标检测方法。这几类算法都具有典型性，仿真过程中使用的仿真实验软件是Matlab R2016a，操作系统为Windows10，电脑主频为2.7 GHz，内存为4 GiB。

对采用的126个波段的AVIRIS图像先利用低秩张量方法进行图像数据恢复，结果如图3所示(以第50波段图像为例)，低秩恢复之后的图像再利用稀疏差异指数进行异常目标检测，结果如图4所示。

图3 图像数据恢复后的高光谱图像(第50波段)Fig.3 The hyperspectral imagery after imagerestoration(the 50th band)

图4 5种算法的异常检测结果Fig.4 Anomaly detection results of five algorithms

从检测结果能看到，LRTD-SR算法异常目标检测精度明显高于其他4种算法。LRTVTD-SR算法虽然也先进行了图像恢复，再采用稀疏表示方法进行异常检测，但算法有效性差于LRTD-SR算法。其他的LSD算法、KRX算法和RX算法异常能力明显低于LRTD-SR算法。

图4是设定像元总数为400时得到的检测结果。为了更好地验证LRTD-SR算法的有效性和精确度，选取从0～200个像元，间隔为10，即可得到总像元数变化过程中算法的检测能力，图5从检测到的目标像元数占总像元数、虚警的像元数占总像元数这两个角度比较了5种算法的检测能力。

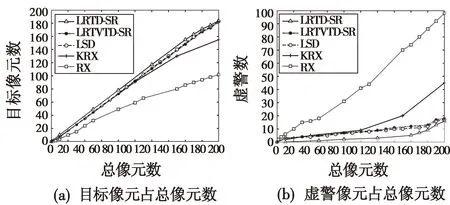
图5 检测到的目标像元和虚警像元占总像元数的比较Fig.5 Comparison of the pixel number of detected targets and false detected targets

通过图5可得，LRTD-SR算法无论是在检测到的目标像元数还是虚警像元数方面都优于其他几种算法，说明该算法具有较好的精确度和鲁棒性。虽然LRTVTD-SR算法也先进行了图像质量恢复，再利用稀疏表示进行异常检测，但是算法检测精度不高，主要是图像质量恢复效果一般；LSD算法作为经典的基于稀疏表示的异常目标检测算法，具有较好的检测性能，但是由于对高光谱图像的空间谱和光谱协同处理不够，算法检测能力有一定局限性；KRX算法、RX算法作为经典的非线性核函数、线性两类异常目标检测算法，主要是从光谱角度对高光谱进行异常目标检测，算法检测性能差于其他几种算法。因此，LRTD-SR算法具有较好的算法检测性能。

ROC特性分析曲线是高光谱图像进行异常目标检测算法性能评价的重要指标之一，体现了检测概率Pd和虚警概率Pf之间的变化关系，分别定义为

(14)

(15)

其中：NH为算法能够检测到的真实目标像元数；NT为被检测的高光谱图像含有的真实目标像元数；NF为算法检测到的高光谱图像含有的虚警像元数；NA为被检测的高光谱图像的总像元数。

图6所示为5种算法的ROC性能检测对比情况。

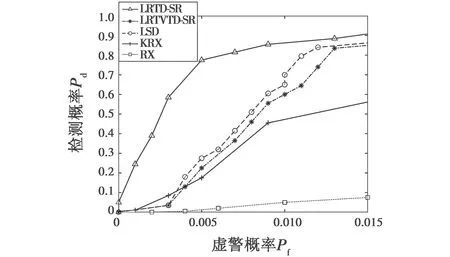
图6 5种算法的ROC性能检测比较

由图6可知，比较LRTD-SR算法、LRTVTD-SR算法、LSD算法、KRX算法和RX算法的ROC曲线能看到，LRTD-SR算法在相同的虚警概率下，检测概率远远高于其他几种算法，而且具有一定的鲁棒性。因此，综合前文提到的LRTD-SR算法仿真验证结果可知，提出的算法能够较好地从高光谱图像中检测出异常目标信息，LRTD-SR算法的检测精确度、有效性和鲁棒性都非常好。

3 结论

为了获得更好的高光谱图像异常目标检测性能，充分利用高光谱图像的光谱特性和空间特性，提出了联合低秩张量和稀疏表示(LRTD-SR)的高光谱异常目标检测新算法。该算法利用低秩张量方法实现高光谱图像的质量恢复和提升，使得高光谱图像中含有的异常目标信息更加突出；然后引入稀疏表示理论，利用稀疏差异指数进行异常目标检测。通过仿真实验比较，提出的LRTD-SR算法具有较高的目标检测率、较低的虚警率和一定的鲁棒性。

但是，通过对整个仿真实验过程的分析发现，算法和实验过程还有一定的局限性：一方面，需要更多的高光谱图像数据集作为实验对象；另一方面，由于参数选择方法的原因，所提的LRTD-SR算法可能并不总能提供令人满意的检测性能，算法的普适性需要更多的实验处理加以改进。这些将是未来研究工作的重点。