非均匀采样系统的无模型自适应准滑模控制
2023-02-13叶金鑫谢丽蓉王宏伟
叶金鑫, 谢丽蓉, 王宏伟
(1.新疆大学,乌鲁木齐 830000; 2.大连理工大学,辽宁 大连 116000)
0 引言
随着现代工业的飞速发展,简单的系统已不能满足日常的工作需要,因此系统也变得越来越复杂。然而,受不同环境条件的限制,越来越多的系统采用了不同的工作频率,所以就有了多率采样数据系统,简称多率系统,该系统拥有许多优点,例如,在增加控制系统复杂性的同时也提高了控制性能[1-3]。
许多学者在输入非均匀刷新和输出周期采样系统方面进行了系统辨识[4-7]和控制的研究。例如在控制方面,文献[8]利用通信序列的概念和推广技术,设计了基于线性矩阵不等式的多输入多输出网络系统的输出反馈控制率,实验表明,输出反馈控制速度快,控制效果好;文献[9]通过将刷新时间间隔作为一个延迟变量,将各个延迟变量的大小的动态变化视为子系统之间的切换来设计切换控制速率,从而实现控制效果;文献[10]考虑到一种访问介质因素的影响,采用开关调度矩阵使网络通信转换成控制系统,利用多个子系统设计反馈控制器,取得良好的控制效果;文献[11]基于网络随机系统的耗散控制问题,通过建立随机环境下的积分不等式(Wirtinger不等式的对应项),得到闭环系统均方稳定和耗散的判据,然后利用该准则,根据线性矩阵不等式的解设计合适的事件触发控制器;文献[12]基于切换原理,利用平均停留时间条件,设计输出反馈控制方法来控制输出反馈;文献[13]针对受有界未知扰动约束的非均匀采样系统,提出一种鲁棒模型预测控制设计方法,采用基于离线状态观测器的准最小-最大鲁棒模型预测控制技术设计输出反馈控制器。虽然在非均系统控制方面取得很多成果,但大多数都集中于线性系统。
近年来,对于非均匀采样的非线性系统辨识已经获得了许多研究成果,但是控制非均匀采样的非线性系统方法却并不多,常见的大部分系统都还是非线性的。目前,对于非线性系统的自适应控制已有很多研究成果,包括自适应鲁棒控制[14]、自适应整体滑模控制[15]、滑模预测控制[16]、鲁棒自适应容错控制[17]和自适应模糊规划最优控制[18-19]、模型参考自适应控制,但是这些方法基本上需要知道系统的确切模型。但是,大多数工业具有大时滞、强耦合的系统,并且很难获得准确的数学模型,设计的控制器通常无法令人满意。神经网络被称为万能逼近器,自适应神经网络和自适应模糊控制不需要精确的数学模型来设计控制器,该控制器也属于无模型自适应控制。目前,大多数系统具备非线性、大时滞强耦合特性,且存在建模困难、难以设计高精度的控制器等问题。值得庆幸的是,文献[20-22]提出了一种无模型自适应控制,这是一种通过线性化设计的控制器,它在离散非线性系统的等效数据点上使用了一种新的动态方法,该方法设计简单,易于实现,不需要知道系统的确切模型,只需要知道系统的输入和输出数据即可。此控制方法应用广泛,如化工、机械、航空、导航和电气等[23-28]。针对非均匀采样非线性系统,文献[29]提出了一种利用支持向量回归建模,设计了预测控制算法;基于当前工作点之处的等价线性化数据模型,在投影算法计算下,文献[30]利用输入输出数据的伪雅可比矩阵在线估计,设计出了相应的无模型自适应控制器。鉴于上述分析,常规的非均匀采样非线性离散系统的无模型自适应控制未考虑存在外界扰动情况,针对这一问题,本文提出了一种无模型自适应准滑模控制算法。
1 问题描述
1.1 非均匀采样非线性模型
非均匀采样非线性系统结构图见图1。
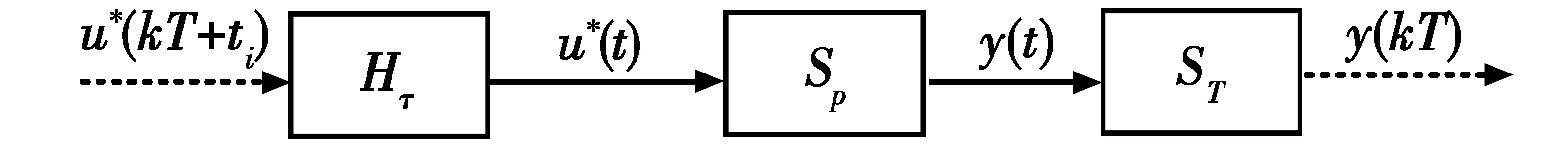
图1 非均匀采样非线性系统结构图Fig.1 Structure diagram of a nonlinear system with non-uniform sampling
其中,Hτ为非均匀采样系统零阶保持器,刷新间隔为{τ1,τ2,…,τp},非均匀采样信号u*(kT+ti)(t0=0,T=ti=ti-1+τi=τ1+τ2+…+τi,i=1,2,…,p)经过Hτ刷新生成连续控制输入信号u*(t),u*(t)经过非线性连续系统Sp生成输出信号y(t),y(t)经过采样器ST以周期T进行采样,采样出离散输出信号y(kT),T=τ1+τ2+…+τi,i=1,2,…,p(T也称帧周期或者框架周期)。
设图1中Sp的状态空间方程为
(1)
式中:y(t)∈R1×1,为输出信号;u*(t)∈Rp,为输入信号;x(t)∈Rn,为状态向量;Γ(·),h(·)为未知的非线性函数。式(1)中u*(t)满足如下关系
(2)
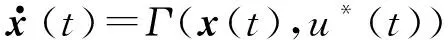
(3)
采用提升技术,构造提升变量
(4)
此时,可将系统式(3)转换成如下离散系统,即
(5)
1.2 线性模型与非线性模型的关系
在连续过程的线性状态空间模型为
(6)
式中,Αc∈Rn×n,Bc∈Rn×p,C∈R1×n,均为矩阵。
由1.1节可知,采样数据分别为u*(kT+ti),i=1,2,…,p-1和y(kT),并且在一个帧周期T内完成离散化系统式(6),即
(7)
利用堆栈向量,将式(6)~(7)整理可得如下离散状态空间模型
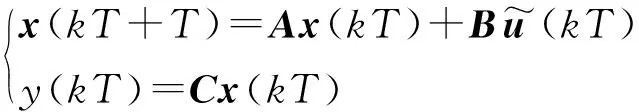
(8)
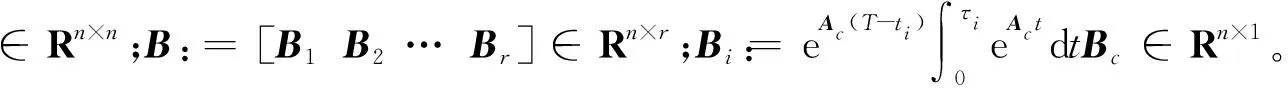
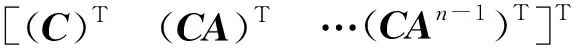
(9)
令In是n阶单位矩阵,系统式(8)可等价为
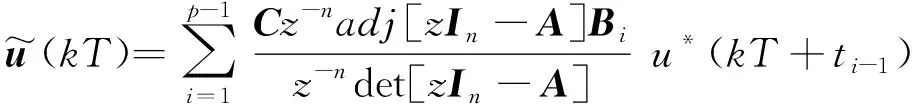
(10)
也可表示为一般形式
(11)
式中,
i=1,2,…,n。
参考文献[30],利用线性与非线性的关系,结合本文非线性系统式(5)与线性系统式(8)得到
(12)
式中:l=1,2,…,Z,Z为常数;φ(kT)=[y(kT-T),…,y(kT-nT),u*(kT-T),…,u*(kT-nT),u*(kT+t1-T),u*(kT+t1-nT),…,u*(kT+tp-1-T),…,u*(kT+tp-1-nT)]T。
模型式(12)中非线性函数分别是由fl[φ(kT)]在第l个非线性加权函数和gl[φ(kT)]在第l个工作点处的局部线性模型构成。因此,模型式(12)进一步表示为
y(kT)=f[φ(kT)]。
(13)
2 无模型自适应控制
2.1 无模型控制器的设计
模型式(13)是由非均匀输入刷新和周期采样利用提升向量推导出多输入单输出(MISO)系统,因此它又可以表示为
y(kT+T)=f(y(kT),…,y(kT-nyT),
u(kT),…,u(kT-nuT))ny=nu=n-1
(14)
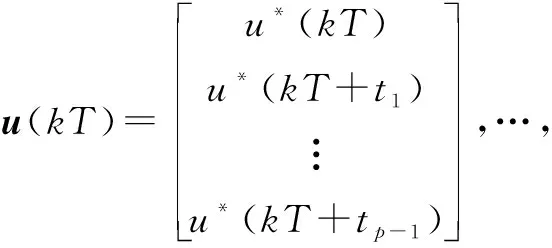
(15)
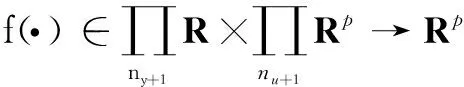
假设1[20-22]非线性系统函数式(14)关于系统控制输入信号u(kT)的偏导数是连续的。
假设2[20-22]非线性系统函数式(14)满足广义Lipschitz条件,即对于任意时刻k1≠k2,k1≥0,k2≥0和u(k1T)≠u(k2T),均有
||
y(k1T+T)-y(k2T+T)||
≤b||
u(k1T)-u(k2T)||
(16)
式中,b>0,为常数。
若非线性系统式(14)满足假设1和假设2,且对所有时刻k有Δu(kT)=u(kT)-u(kT-T)≠0,则系统式(14)可以表示为如下紧格式动态线性化(Compact Form Dynamic Linearization,CFDL)的一类泛模型
Δy(kT+T)=ΦT(kT)Δu(kT)
(17)
式中:Δy(kT)=y(kT+T)-y(kT);Φ(kT)=[Φ1(kT) …Φp(kT)]T∈Rp×1,Φ(kT)为伪雅可比矩阵,且满足||
Φ(kT)||
≤b。
考虑如下性能控制指标函数
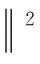
(18)
将式(17)代入指标函数式(18),λ>0,为权重因子。对u(kT)极小化,并令其等于零,即
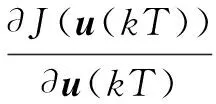
(19)
整理得到如下投影算法
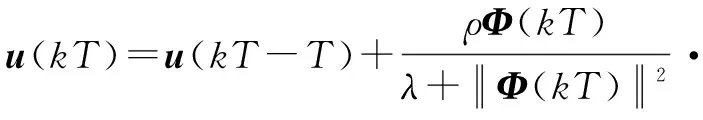
(20)
式中,ρ为额外加入的步长因子,ρ∈(0,1],目的是使该算法具有更强的灵活性。
对于一般系统来说,即使是简单的线性系统,伪雅可比矩阵Φ(kT)也一般是未知、时变的。因此,为实施控制律式(20),采用如下性能指标在线估计伪雅可比矩阵Φ(kT)的值,即
(21)
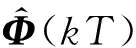
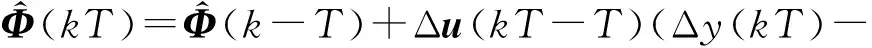
(22)
由于伪雅可比矩阵在线估计算法中需要求矩阵逆,如果当系统输入维数极大时,矩阵求逆运算是极耗时的。所以对伪雅可比矩阵估计算法进行改进,得到新的估计算法为
(23)
Δu(kT-T)||
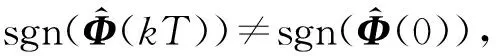
结合式(17)、式(23),有
(24)
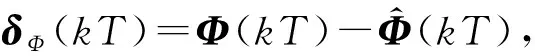
2.2 无模型滑模控制器的设计
滑模控制的非线性表现为控制的不连续性,即系统的“结构”不是固定的,可以根据状态自动连续变化。动态过程中,系统的状态迫使系统遵循预定目标“滑模”路径运动;离散变结构自适应控制对内部参数的扰动和外部扰动具有很强的适应性和鲁棒性。由于自适应控制主要基于系统的精确数学模型,因此,自适应变结构控制的大多数离散理论结果存在对被控系统数学模型结构的依赖和未建模动态两个问题。无模型自适应控制不需要知道系统的确切模型,因此设计无模型滑模控制,具体如下所述。
定义滑模平面函数
s(kT)=cTE(kT)
(25)
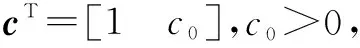
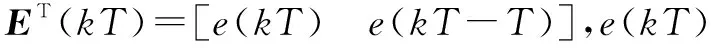
e(kT)=yr(kT)-y(kT)
(26)
式中,yr(kT)为输出向量的期望跟踪轨迹,假设其为有界序列。
采用离散趋近律
s(kT+T)=(1-q)s(kT)-ωsgn(s(kT))
(27)
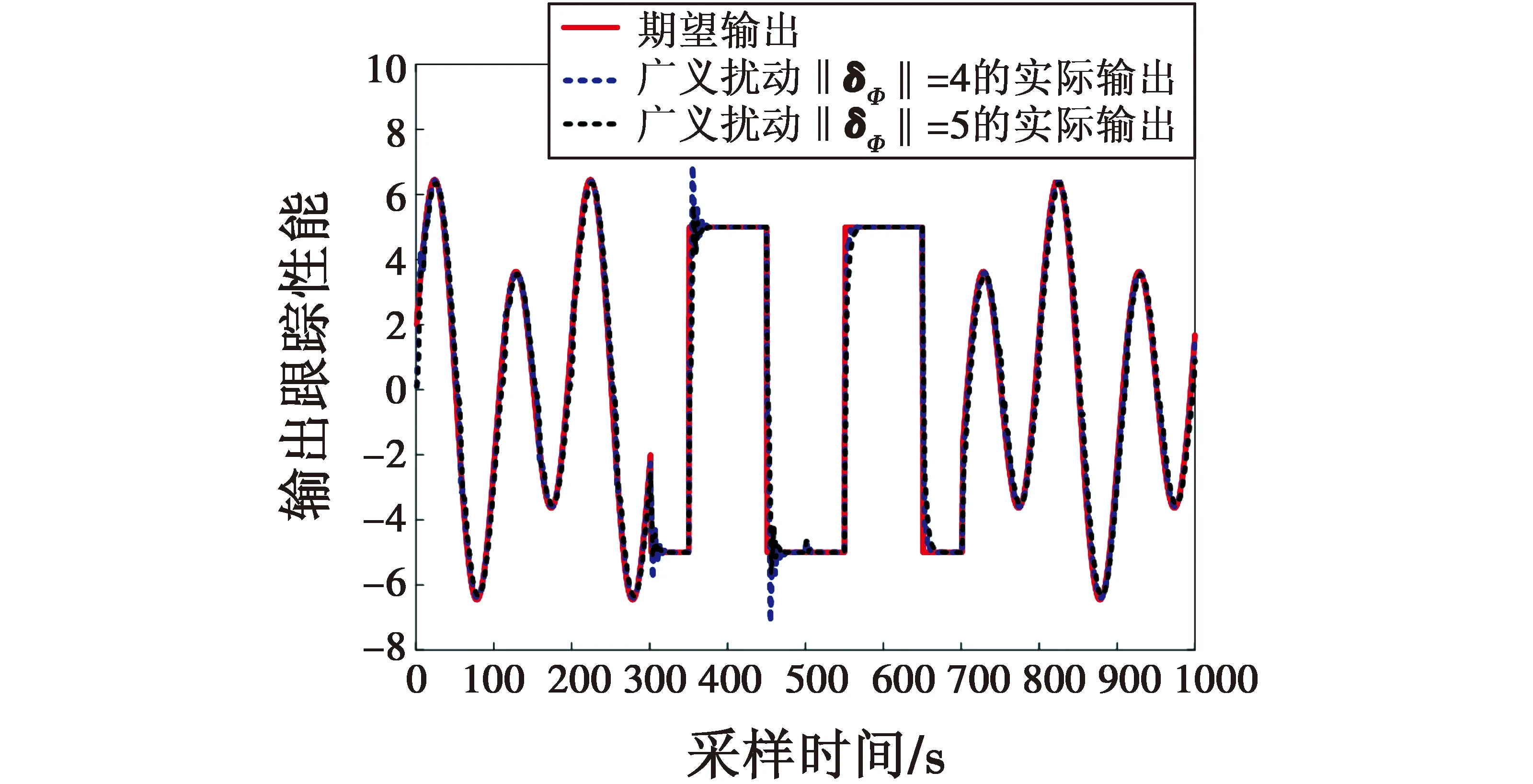
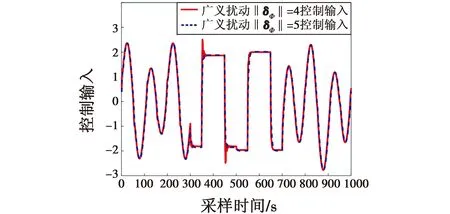
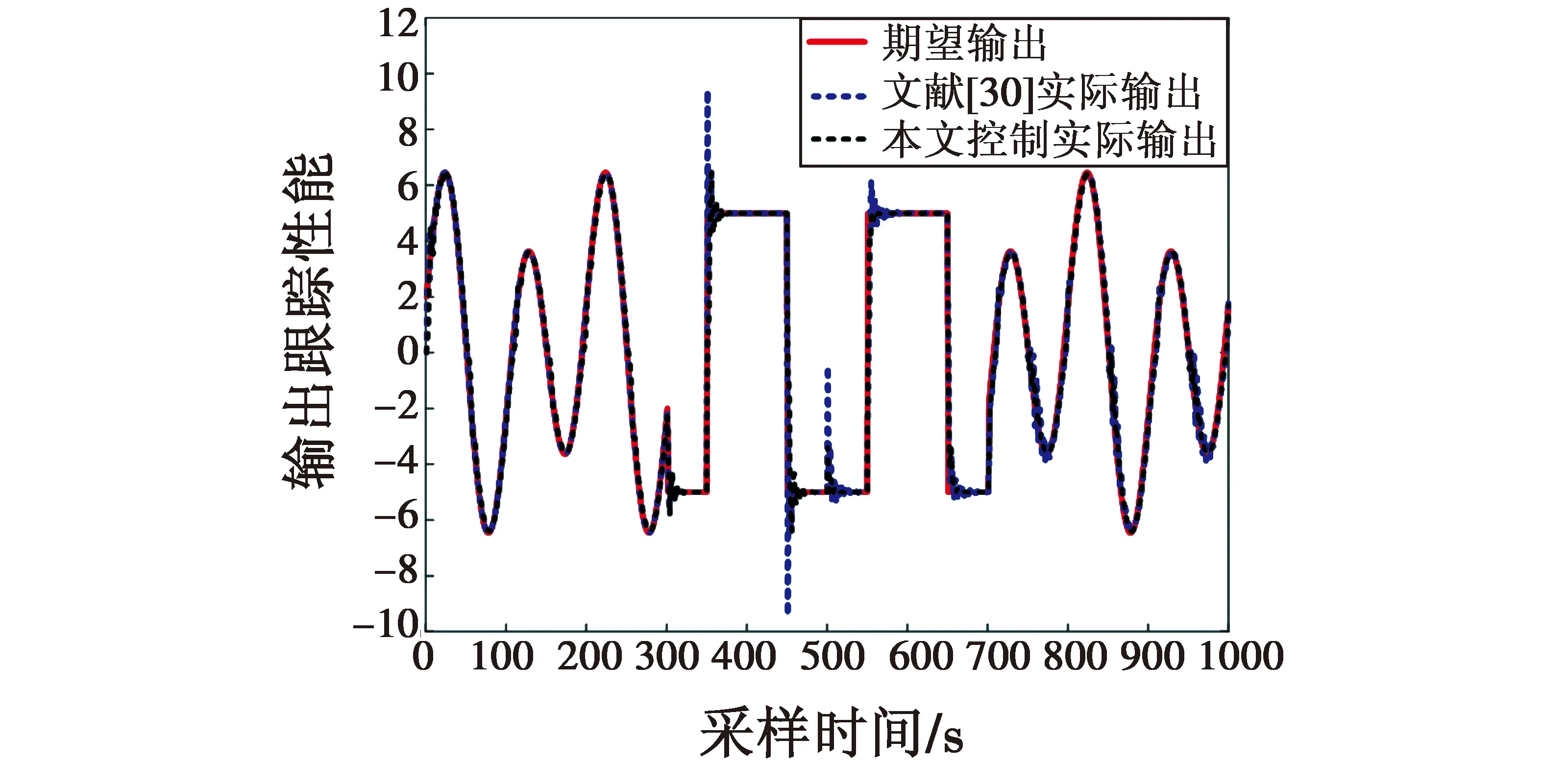
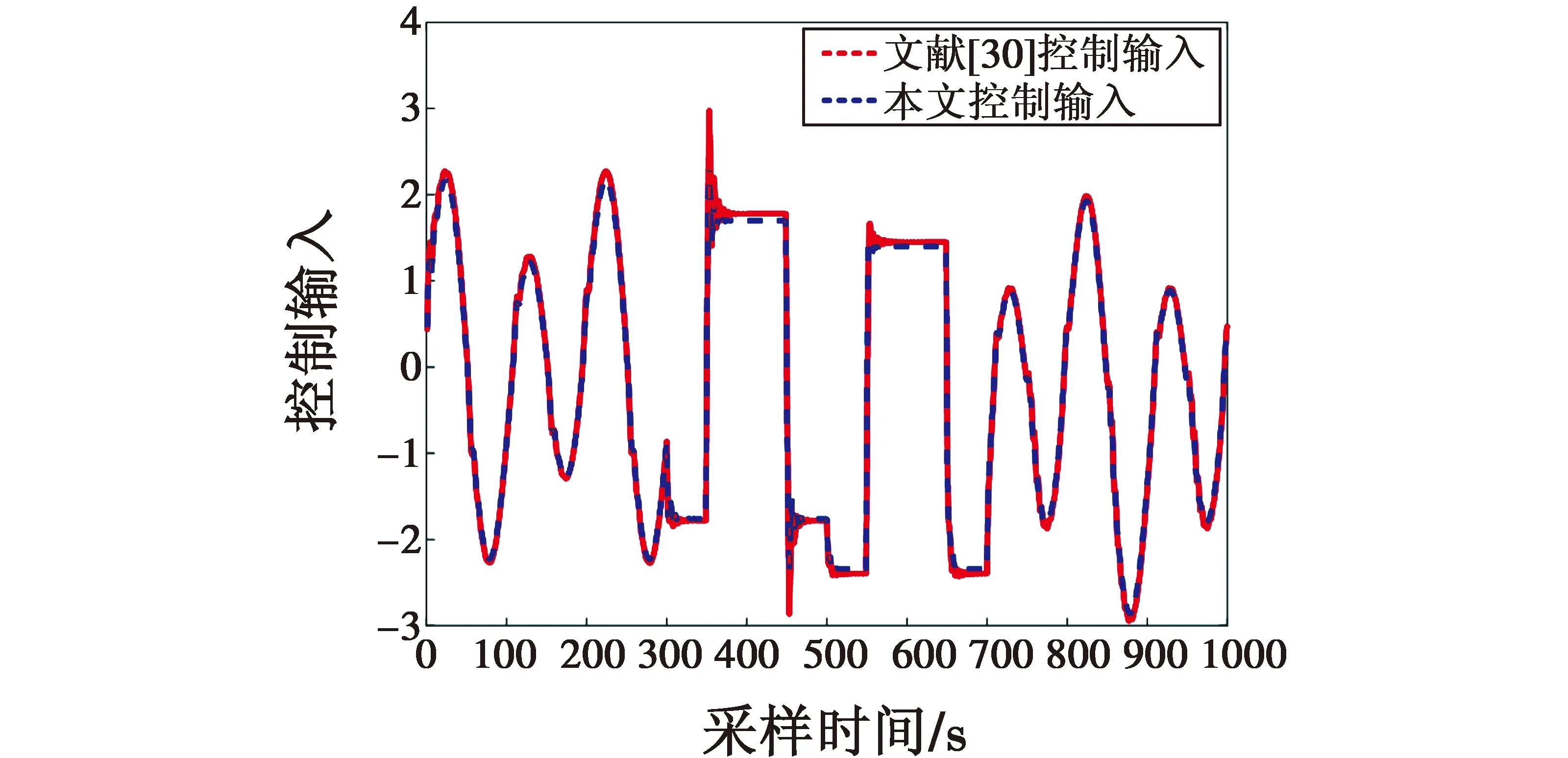
式中,设计参数q,ω满足ω>0,0 等效控制为 s(kT+T)=(1-q)s(kT)-ωsgn(s(kT))= (28) 通过式(25)~(28),得 cTE(kT+T)=e(kT+T)+c0e(kT)= (29) 整理式(29)得 e(kT+T)=(1-q)s(kT)- (30) 由跟踪误差的定义可得 yr(kT+T)-y(kT+T)=(1-q)s(kT)- (31) 结合式(24)、式(31)得 (32) 通过整理式(32),可得到控制律为 Δu(kT)=(yr(kT+T)-y(kT)-(1-q)s(kT)+ (33) 得出控制律后,代入式(25),求得稳定多项式c0的取值范围为 (34) 因此可得到无模型自适应准滑模控制器为 u(kT)=u(kT-T)+Δu(kT) (35) 由式(23)、式(35)可得控制算法如下所述。 1) 参数估计算法 (36) Δu(kT-T)|| 2) 控制器算法 (37) 定理1[20-22]若假设1、假设2存在,被控系统式(24)采用控制器式(33)进行控制,在时变参数Φ(kT)采用式(23)进行在线估计的情况下,对于所给定参考信号yr(kT+T)有界,那么会存在:1) 跟踪误差信号e(kT)有界;2) {y(kT)},{u(kT)}是有界序列。 证明。 2) 跟踪误差的有界性证明。 利用李雅普诺夫定义正定函数如下 (38) 由V(kT)的定义有V(kT)>0成立,且 (39) 最终式子的前3项都小于0,只要选ω足够小就能保证ΔV(kT+T)<0,且根据定义及系统各给定的初始值,可知V(0)有界。也就意味着系统在控制律式(33)作用下是稳定的,系统跟踪误差收敛到零的领域内,即{e(kT)}是有界的。 3) 输出信号的有界性证明。 由跟踪误差的定义 e(kT)=yr(kT)-y(kT) (40) 由于已知期望跟踪轨迹{yr(kT)}有界,又由上步证明{e(kT)}有界,所以{y(kT)}也是有界的。 4) 控制信号的有界性证明。 由式(36)可知,系统具有一个全局渐近稳定的零动态,因此存在常数M1,M2,k0T满足 (41) 已证明{y(kT)}有界,所以由式(41)可知{u(kT)}也是有界的。 为了验证本文所设计无模型自适应滑模控制算法的有效性,考虑非均匀采样的非线性系统 (42) 期望输出信号为 (43) 选取权重因子μ=0.9,步长因子η=0.5。伪雅可比矩阵估计误差(外界扰动)|| δΦ|| =4和|| δΦ|| =5对输入非均匀刷新输出均匀采样系统进行干扰,利用式(36)~(37)设计的控制器对上述系统进行控制。 图2所示为输出跟踪曲线,图3所示为控制输入信号。 图2 输出跟踪曲线Fig.2 Output tracking curve 图3 控制输入信号Fig.3 Control input signal 由图2可以看到,当伪雅可比矩阵估计误差||δΦ||=4时,闭环系统反应很快,但超调量却很大;当伪雅可比矩阵估计误差|| δΦ|| =5时,闭环系统反应慢,超调量却不大了。从图3可以看到,无模型自适应控制与滑模控制相结合,减少了干扰对系统控制的影响,并有效地提高了控制效果。 将本文所提出的无模型自适应准滑模控制算法与无模型自适应控制算法[30]进行对比分析。 图4所示为输出跟踪对比曲线,图5所示为控制输入对比信号。 图4 输出跟踪对比曲线Fig.4 Output tracking curve comparison 由图4可以看出,本文所设计的无模型自适应准滑模控制算法跟踪效果明显优于文献[30]控制算法,收敛性能好、超调量低,能更好地贴进参考轨迹曲线,且系统的抖振更低。从图5的仿真效果来看,非均匀采样非线性系统结构发生突变或者外部函数的扰动,无模型自适应准滑模控制的输出仍能够很好地跟踪期望输出。 图5 控制输入对比信号Fig.5 Control input signal comparison 图6所示为误差对比曲线。 图6 误差对比曲线Fig.6 Comparison of error curves 由图6可以看到,本文控制算法误差轨迹曲线相比文献[30]控制算法误差轨迹曲线波动小,在每个时间点处的误差也小。 表1所示为本文算法与文献[30]算法性能比较。 表1 本文算法与文献[30]算法性能比较 由表1进一步可以看出,本文算法的均方根误差小,因此所提出的控制算法具有更好的控制跟踪效果。 针对非均匀采样非线性系统存在外界扰动造成难以控制的问题,提出了无模型自适应准滑模控制。系统动态线性化过程的伪雅可比矩阵参数估计误差被认为是一种干扰,采用滑模控制方法设计了动态线性化模型的控制器。该算法的特点是结合滑模控制的鲁棒性,减少干扰对系统控制效果的影响,有效提高控制效果,分析了该控制算法的稳定性。对于输入非均匀周期刷新和输出非均匀周期采样离散非线性系统,即利用堆栈向量转换成多输入多输出型的一类系统,将是下一步工作中需要进行讨论和研究的内容。
cTE(kT+T)
(1-q)s(kT)-ωsgn(s(kT))
ωsgn(s(kT))-c0e(kT)
ωsgn(s(kT))-c0e(kT)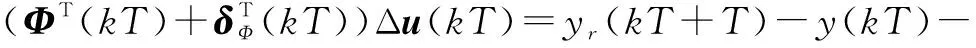
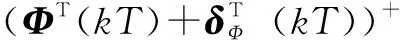
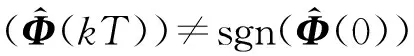
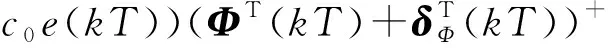
3 性能分析
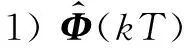
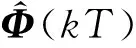
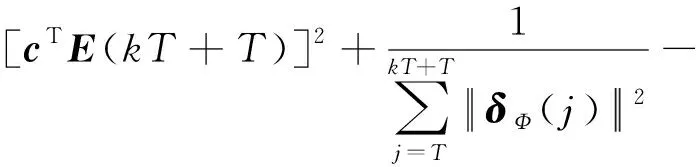
4 仿真实例
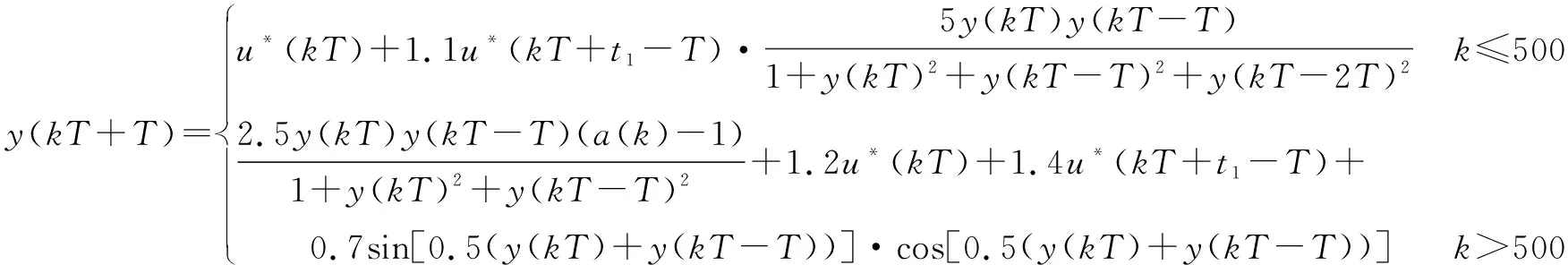

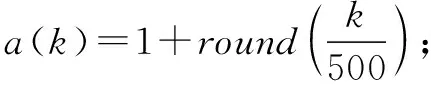


5 结论
