基于熄弧后主谐振频率的系统电容电流测量方法误差分析

张 帆，薛永端，徐丙垠

（1. 中国石油大学（华东）新能源学院，山东省 青岛市 266580；2. 山东理工大学电气与电子工程学院，山东省 淄博市 255000）

0 引言

在谐振接地（中性点经消弧线圈接地）系统中，系统（对地）电容电流的精确测量对于接地故障的有源补偿［1］和故障消弧［2］等具有重要意义。若无法精确测量系统电容电流，可能使得消弧线圈型号选择和容量配置不合理，系统失谐度过大或过小，进而使得故障点残流增大，影响系统的熄弧效果，可能产生谐振或者拍频［3］等现象，引起较为严重的过电压，使得故障危害程度加大。此外，系统电容电流的作用还体现在故障检测［4-5］、无功补偿［6］和谐振抑制［7］等方面。因此，系统电容电流测量的误差分析有助于指导相关测量设备的选型以及参数提取方法的设计，进而实现系统电容电流的精确测量。

根据《中性点不接地系统电容电流测试规程》［8］规定，目前系统电容电流测量方法主要分为直接测量法和间接测量法。直接测量法通过人工金属性单相接地故障试验直接测量故障点电流，从而获得系统电容电流，该方法测量可信度高，但是安全风险大，现场条件要求严格［9］，现已很少采用。间接测量法无须人工金属性单相接地故障试验，通过接入某些元件或注入特定的测量信号进行测试，计算得到系统电容电流，如信号注入法［10］、偏置阻抗法［11］、谐振法［12］等，这些间接测量方法在系统配置合理、测量结果准确的情况下一般能够得到比较准确的结果，但是测量方法操作复杂，需要利用一次设备进行作业，具有一定危险性，而且其测量精度受多方面因素影响。因此，为了对以上测量方法起到辅助补充的作用，文献［13］提出一种基于单相接地故障熄弧后暂态信息的系统电容电流测量方法，该方法为被动测量方式，主要利用熄弧后暂态过程的主谐振频率进行测量，不需要增设专用的测量设备或者调整现有设备的运行状态，具备成本低廉、操作简单和结果准确的特点。

文献［13-14］的分析表明:故障点熄弧后的暂态信息可以用来反映消弧线圈电感值与系统对地电容值之间的谐振约束关系，该谐振约束关系不受消弧线圈类型、故障点状态等影响，所以在系统结构固定的情况下，系统对地电容值也固定。可以根据熄弧后的暂态信息计算系统失谐度，进而结合熄弧前消弧线圈电流实现系统电容电流的测量。

本文首先针对文献［13］提出的基于谐振接地系统单相接地故障熄弧后暂态信息的系统电容电流测量方法进行测量允许误差分析；然后，提出测量过程中的主谐振频率测量误差要求；最后，通过MATLAB/Simulink 仿真进行验证。

1 系统电容电流测量方法

图1 为谐振接地系统单相接地故障的等效电路［15］。其中:L0为补偿电感，含消弧线圈、接地变压器与主变压器的等效电感；RL为熄弧后恢复过程中系统等效有功损耗电阻，含消弧线圈的零序电阻和接地变压器的零序电阻；C为系统中所有线路的零序电容之和；LK为故障点到母线之间线路的零模与线模参数及主变线模参数的等效电感之和；RK为故障点到母线之间线路的零模与线模参数、主变线模参数及故障点过渡电阻的等效电阻之和；uf=Umsin(ω0t+φ)为虚拟电源，其中，φ为故障相接地瞬间电源电动势相角，Um为电源电压幅值，ω0为工频角频率；if为故障点电流。

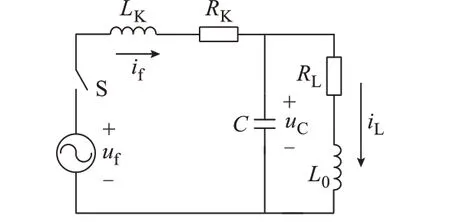
图1 谐振接地系统单相接地故障等效电路Fig.1 Equivalent circuit of single-plase-to-ground fault of resonant grounding system

根据文献［16］可得，当谐振接地系统发生单相接地故障时，在故障点电流过零熄弧后，母线零序电压uC与消弧线圈电流iL均为衰减的正弦分量，而主谐振角频率ωh与衰减因子δh的关系为:

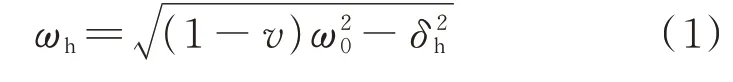
式中:v为系统失谐度。

由于暂态过程仅与补偿电感（含消弧线圈电感与接地变压器电感）、系统对地电容以及系统等效阻抗有关，与故障条件（如故障点位置、故障初相角等）、故障点状态（如接地电阻大小、电弧稳定程度等）无关［13］，因此衰减因子δh和主谐振角频率ωh仅与L0、C等参数有关。

由式（1）可得系统失谐度v为:

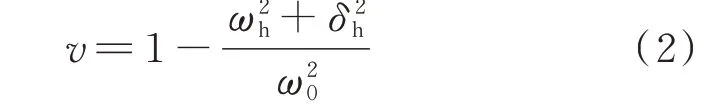
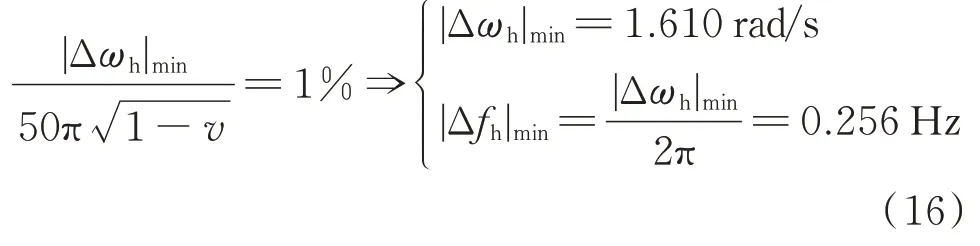
因此，可以根据熄弧后暂态过程的衰减因子δh和主谐振角频率ωh计算得到当前的系统失谐度v。

一般地，系统失谐度v定义为:

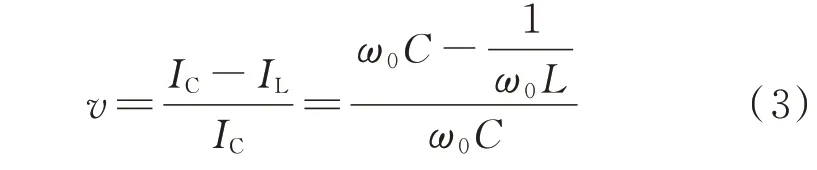
式中:IC为系统电容电流；IL为熄弧前消弧线圈电流有效值；L为消弧线圈电感。

当系统发生金属性单相接地故障时，IL为:

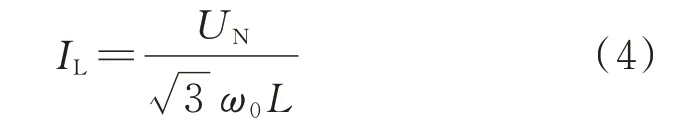
式中:UN为系统额定电压。

由于系统发生单相接地故障时过渡电阻的存在，熄弧前测量得到的母线零序电压有效值UC与系统额定相电压不相等。由于系统频率偏移的存在，熄弧前测量得到的消弧线圈电流IL和母线零序电压UC的频率并不一定等于50 Hz。根据电路的齐性定理［17］，金属性单相接地故障熄弧前消弧线圈电感电流有效值IL可以通过归算的方法得到，即

式中:I′L为测量得到的消弧线圈电流；f0为工频，取值为50 Hz为测量得到的系统频率。

由式（5）和式（6）可得IC为:

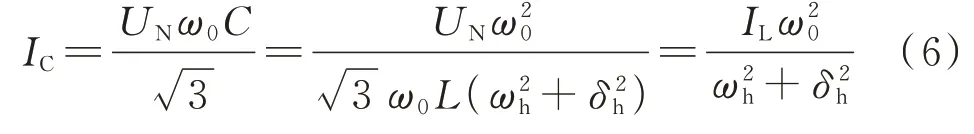
主谐振角频率ωh的取值一般接近或者大于工频角频率ω0=100πrad/s；而衰减因子δh的取值一般为9.42～21.9 s−1［16］。显 然，ωh在 数 值 上 远 大 于δh，因此，衰减因子误差对系统电容电流误差的影响较小，仅为前者的0.5%左右，在测量误差分析时可以近似忽略。

当忽略衰减因子时，式（2）可以改写为:

式（6）可以改写为:

2 误差分析

2.1 技术要求

根据《自动跟踪补偿消弧线圈成套装置技术条件》［18］（以下简称技术条件）规定，对于自动跟踪补偿消弧线圈成套装置，系统电容电流的测量误差技术要求如下:

1）当系统电容电流IC≤30 A 时，测量误差应不大于1 A，即|ΔIC|≤1 A；

2）当系统电容电流30 AIC≤100 A 时，测量误差应不大于3%IC，即|ΔIC|≤3%IC；

3）当系统电容电流IC>100 A 时，测量误差应保证残流不大于7.5 A，即If≤7.5 A。

根据现场运行的经验，当系统电容电流IC>100 A 时，应保证系统电容电流测量误差不大于5.5 A，即|ΔIC|≤5.5 A。

因此，系统电容电流IC与系统电容电流测量误差ΔIC的关系如附录A 图A1 所示，其中，红色阴影区域即为允许的系统电容电流测量误差取值范围。

同样地，在技术条件中规定，对于消弧线圈电流的测量相对误差不大于2%，即

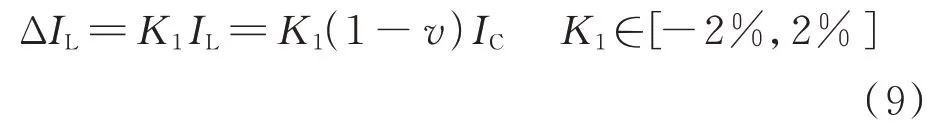
式中:ΔIL为消弧线圈电流的测量绝对误差；K1为消弧线圈电流的测量相对误差因子。

2.2 系统电容电流测量误差

由式（8）可知，系统电容电流测量精度受消弧线圈电流IL和主谐振角频率ωh的测量精度影响，且对于消弧线圈电流IL的测量在技术条件中已有明确规定（式（9））。

令式（8）中的IC分别对IL和ωh求偏导，可得:

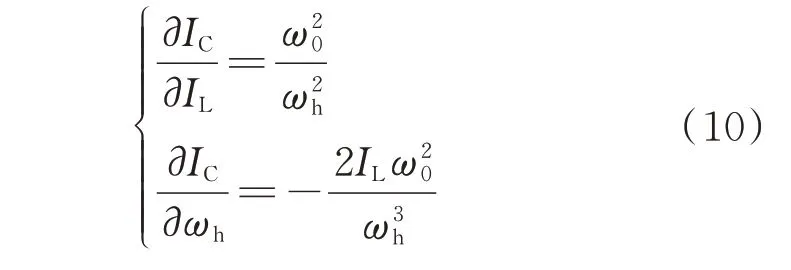
因此，利用多元函数全微分可得系统电容电流IC的测量绝对误差为:

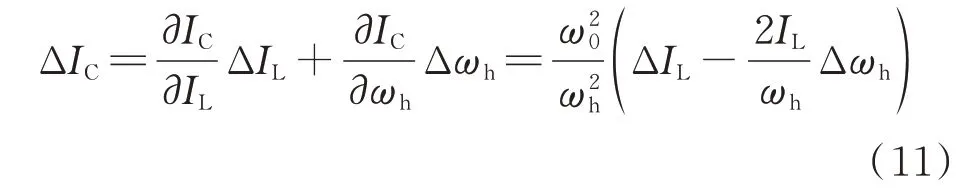
式中:Δωh为主谐振角频率的绝对误差，如式（12）所示。

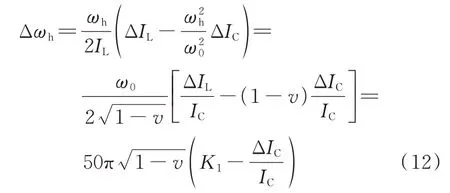
系统失谐度一般为−10%～−5%［19］，然而经现场调研发现，存在部分谐振接地系统的系统失谐度偏差较大，其取值范围为−50%～50%。

2.3 误差分析

针对式（12）分析主谐振角频率的测量误差，且式（12）的最小值即为主谐振频率测量的最大允许误差。本节将对系统失谐度在−10%～−5%的情况给出主谐振频率的误差分析，并对系统失谐度取其他值的情况给出说明。

首先，计算主谐振频率最大允许误差，即对应系统电容电流测量误差最大时的最小频率误差绝对值。当一种频率测量方法的误差小于最小频率误差绝对值时，即可保证系统电容电流的计算误差满足相关技术条件的最低要求。

1）当系统电容电流IC≤30 A 时，根据技术要求可得:

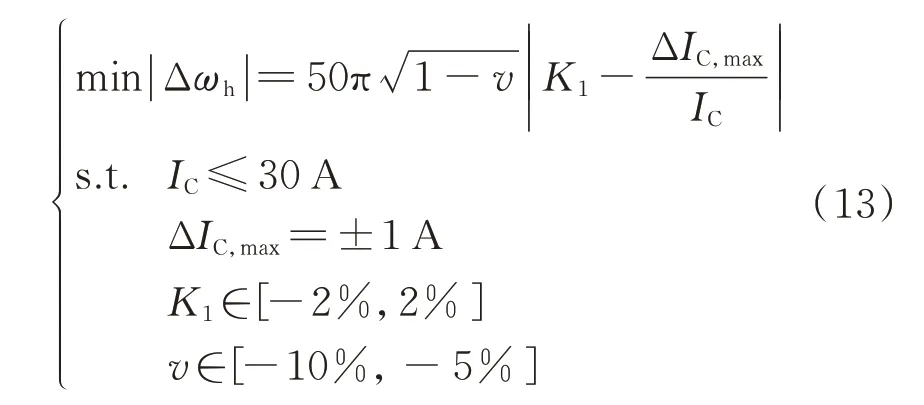
式中:ΔIC，max为系统电容电流测量误差的最大值。

显而易见，为了使角频率误差绝对值|Δωh|取最小值，系统失谐度v=−5%。因此，式（13）转化为双变量线性规划问题［20］。如图2 所示，根据图解法进行求解，蓝色阴影区域为可行域，蓝色直线为与目标函数有关的直线簇，在其不断平移过程中可得:当v=−5%、IC=30 A、K1=2% 且ΔIC，max=1 A 或K1=−2% 且ΔIC，max=−1 A 时，|Δωh|取 得 最 小 值|Δωh|min，即

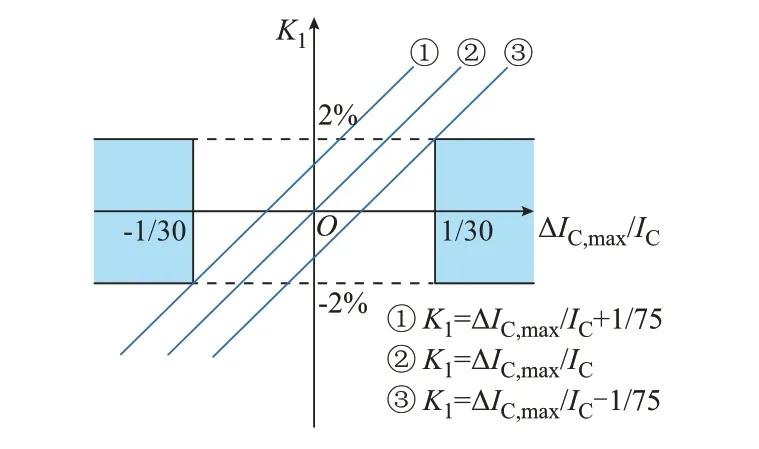
图2 IC ≤30 A 时角频率测量误差分析Fig.2 Error analysis of angular frequency measurement when IC ≤30 A

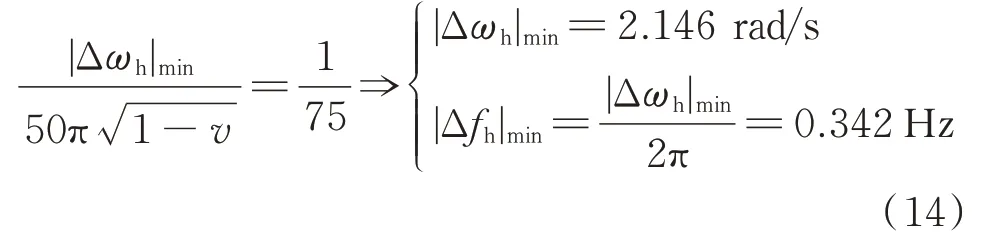
式中:|Δfh|min为主谐振频率误差绝对值的最小值。

2）当系统电容电流30 AIC≤100 A 时，令系统电容电流测量误差因子K2=ΔIC/IC，且最大上下偏差K2，max=±3%，根据技术要求，即

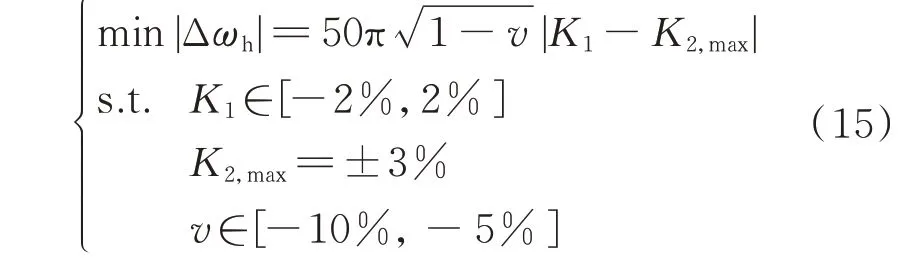
同理，如附录A 图A2 所示，根据图解法进行求解，在不断平移的过程中可得:当v=−5%、K1=2%且K2，max=3%或K1=−2%且K2，max=−3%时，|Δωh|取得最小值，即

3）当系统电容电流IC>100 A 时，如果考虑系统失谐度在−10%～−5%范围内，且由于技术条件中对于故障点残流的限制，那么仅在100 AIC≤150 A 时可以同时满足以上条件。然而，在现场实际运行中，存在部分谐振接地系统的系统电容电流150 AIC≤200 A，此时若继续沿用系统失谐度，则故障点残流将大于7.5 A。因此，从理论上讲，系统失谐度需要取−5%v＜0。出于预防谐振过电压、避免全补偿状态的考虑，设故障点残流变化范围为4 AIf≤7.5 A，此时系统失谐度与系统电容电流的关系如附录A 图A3 所示。

（1）当系统电容电流100 AIC≤150 A，考虑系统失谐度在−10%～−5%时，根据技术要求可得:

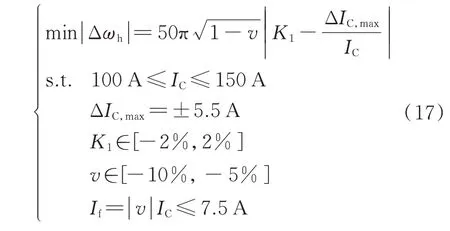
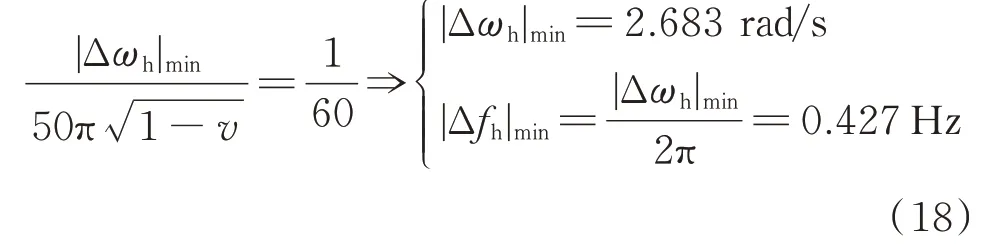
同理，如附录A 图A4 所示，在不断平移的过程中可得当v=−5%、IC=150 A、K1=2%且ΔIC，max=5.5 A 或K1=−2%且ΔIC，max=−5.5 A 时，|Δωh|取得最小值，即

（2）当系统电容电流150 AIC≤200 A，控制系统失谐度−5%v＜0，在预防全补偿时，根据技术要求可得:

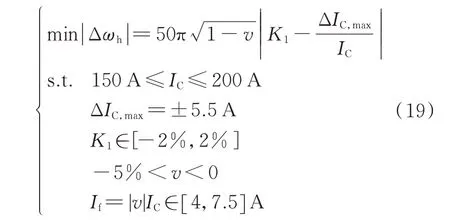
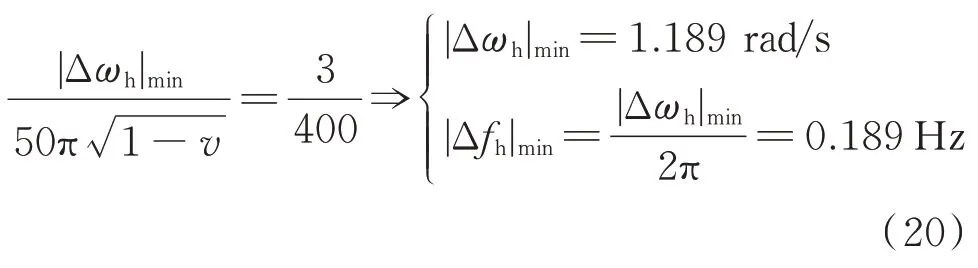
如附录A 图A5 所示，在不断平移过程中，结合附录A 图A3 可得:当v=−2%、IC=200 A、K1=2%且ΔIC=5.5 A 或K1=−2% 且ΔIC=−5.5 A 时，|Δωh|取得最小值，即

在 系 统 电 容 电 流 100 AIC≤150 A 和150 AIC≤200 A 这2 种 情 况 中，ΔIC，max=±5.5 A对IC=150 A 的影响较IC=200 A 更大，且在系统失谐度的控制上，100 AIC≤150 A 时取v=−5%，150 AIC≤200 A 时 取v=−2%，使 得100 AIC≤150 A 时的主谐振频率最大测量允许误差大于150 AIC≤200 A 时的主谐振频率最大测量允许误差。

以上结果同样可以根据单纯形表法［21］或者其他线性规划方法求得。

其次，在实际测量过程中，对于系统电容电流和消弧线圈电流测量误差的要求一般比技术条件中规定的更为严格。因此，分别绘制4 种典型谐振接地系统的主谐振角频率测量误差Δωh随着系统电容电流测量误差ΔIC或系统电容电流测量误差因子K2、消弧线圈电流的测量相对误差因子K1变化的规律，如附录A 图A6 所示。根据实际误差需求可获得相应的主谐振角频率测量误差。

附录A 图A6（a）中，取系统电容电流IC=30 A，系统失谐度v=−5%；图A6（b）中，取系统电容电流IC=100 A，系统失谐度v=−5%；图A6（c）中，取系统电容电流IC=150 A，系统失谐度v=−5%；图A6（d）中，取系统电容电流IC=200 A，系统失谐度v=−2%。

由以上分析可知，在通过测量单相接地故障熄弧后的暂态信息测量系统电容电流的过程中，需要注意的是:

1）在测量主谐振频率的过程中，当系统失谐度在−10%～−5%范围时，要求:对于系统电容电流IC≤30 A 的配电系统，主谐振频率最大测量允许误差为0.342 Hz；对于系统电容电流30 AIC≤100 A 的配电系统，主谐振频率最大测量允许误差为0.256 Hz；对于系统电容电流100 AIC≤150 A的配电系统，主谐振频率最大测量允许误差为0.427 Hz。

2）当系统失谐度−5%v＜0 并预防全补偿时，要求对于系统电容电流150 AIC≤200 A 的配电系统，主谐振频率最大测量允许误差为0.189 Hz。

3）考虑到实际配电网中系统失谐度可能的取值范围为−50%～50%，对于以上4 种情况，其主谐振频率最大测量允许误差将在v=50%时取得，此时其值分别为0.236、0.177、0.295 和0.133 Hz，但是还需考虑是否调整消弧线圈补偿量，并注意故障点残流的限制要求。

4）考虑到系统失谐度的未知性，保证系统电容电流测量的可靠性等，实际的主谐振频率测量装置测量误差选取应小于全部情况的最小值，即0.133 Hz，建议主谐振频率最大测量允许误差统一取0.100 Hz。

3 仿真验证

利用MATLAB/Simulink 搭建谐振接地系统进行仿真模拟单相接地故障，仿真模拟系统的电压等级为10 kV，包含电缆线路、架空线路和混合线路，不同线路类型的参数如表1 所示。其中，R0u、L0u、C0u和R1u、L1u、C1u分别为零序和正序分布电阻、电感和电容。仿真频率为50 Hz。

表1 架空线及电缆线路分布参数Table 1 Distribution parameters of overhead lines and cables

3.1 仿真验证1：系统电容电流IC ≤30 A

仿真验证1 所用的谐振接地系统仿真结构如图3 所示，根据表1 的分布参数，系统对地电容为Ctot，1，set=2.42 μF，对于10 kV 系统，系统电容电流为IC，1，set=18.29 A。

图3 谐振接地系统仿真结构Fig.3 Simulation structure of resonance grounded system

设消弧线圈电感L=956.56 mH（系统补偿度v=−5%），进行1 000 次蒙特卡洛试验，其中，在测量消弧线圈电流和母线零序电压时加入2%的随机波动，分别记录母线零序电压、消弧线圈电流等数据。根据快速傅里叶变换分析，测得熄弧前消弧线圈电流有效值；利用最小二乘矩阵束算法［22］，测量熄弧后母线零序电压或消弧线圈电流的衰减因子δh和主谐振频率fh（fh=ωh/2π）；通过式（8）计算系统电容电流。某次仿真试验的母线零序电压、消弧线圈电流和故障点残流波形如图4 所示。

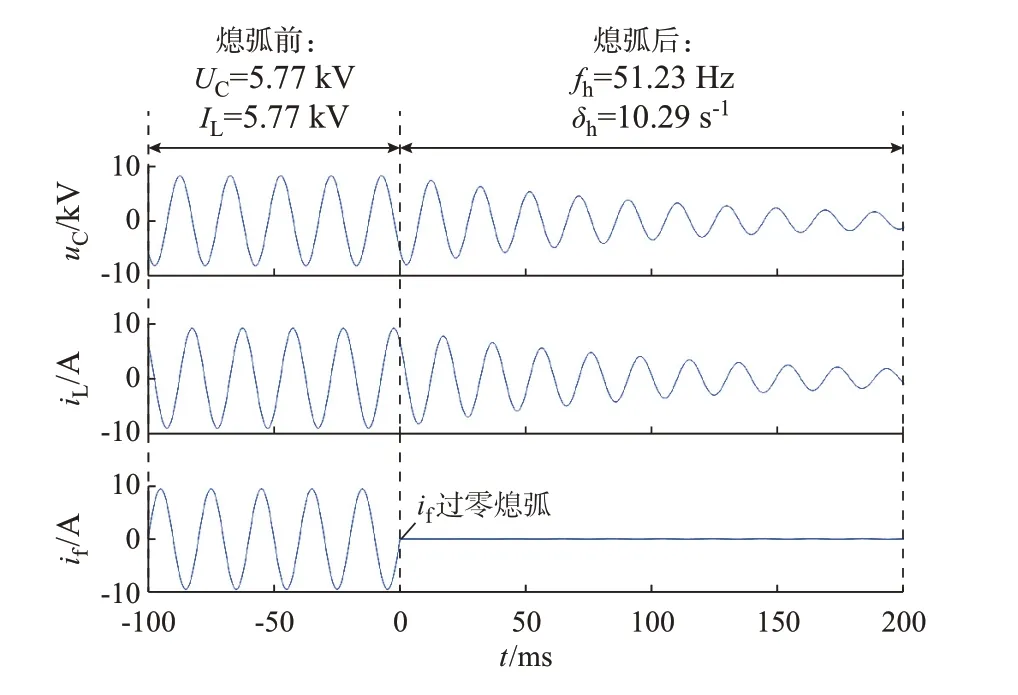
图4 仿真验证1 的试验波形举例Fig.4 Example of test wave in case 1

保持系统失谐度v=−5%不变，在此基础上逐渐改变配电网中的架空线或电缆的长度，使得系统电容电流分别取15、20、25 和30 A。重复以上仿真过程，主谐振频率fh与系统电容电流测量结果IC的关系如图5 所示，其中，红色实线分别表示仿真中不同的系统电容电流设定值IC，1，set，实线附近的两条虚线表示考虑测量误差后的系统电容电流测量结果允许范围，位于虚线范围内的测量结果（图中“+”号表示）满足该系统电容电流设定值下的技术条件要求；反之，位于虚线范围外的测量结果（图中“*”号表示）则不满足。

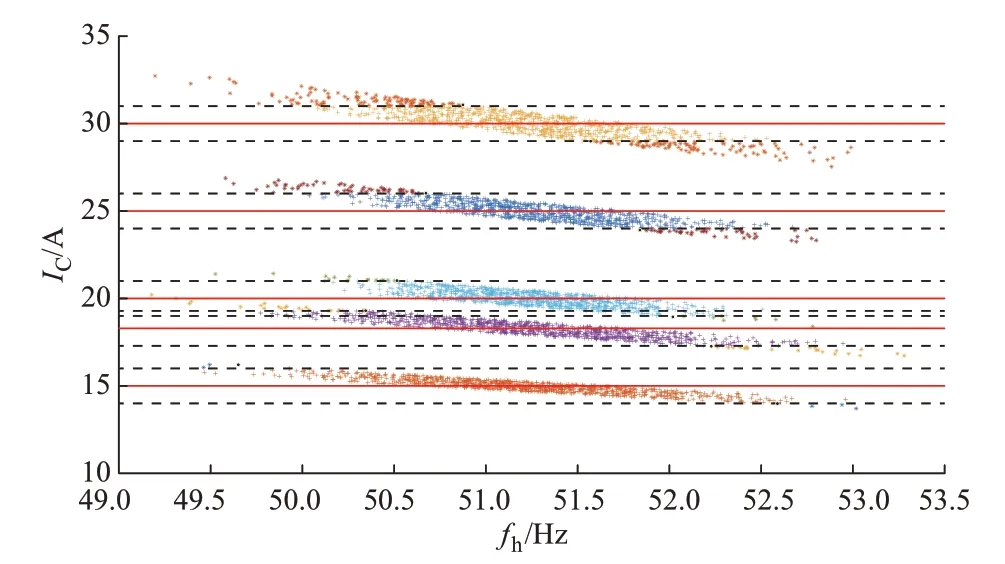
图5 仿真验证1 的主谐振频率与系统电容电流关系Fig.5 Relation between main resonant frequency and system capacitance current in case 1

表2 为仿真验证1 中系统电容电流不同时的主谐 振 频 率 测 量 仿 真 结 果。其 中:fh，1，min和fh，1，max分 别为允许的主谐振频率测量下限和上限；E(fh，1)和S2(fh，1)分别为频率测量结果的数学期望和方差；Δfh，1为 频 率 测 量 误 差，即Δfh，1=min(fh，1，max−E(fh，1)，E(fh，1)−fh，1，min)。因此，应该保证熄弧后的主 谐 振 频 率 测 量 范 围 为E(fh，1)−Δfh，1至E(fh，1)+Δfh，1。表中各变量下标“1”表示仿真验证1 的相关数据，下文仿真验证2、3、4 的相关变量解释不再赘述。

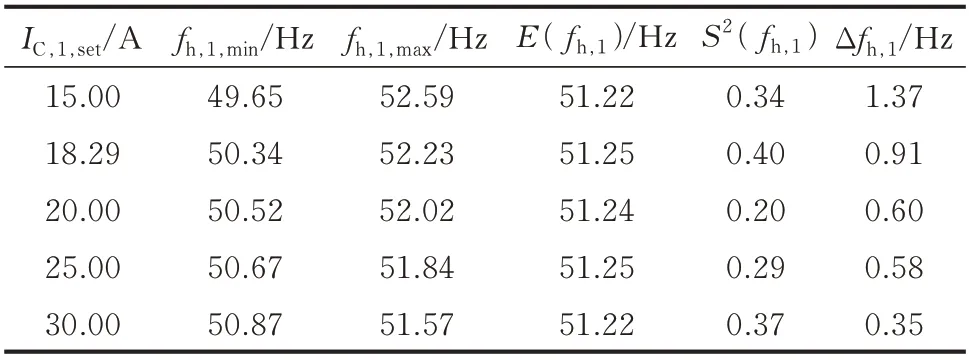
表2 仿真验证1 的主谐振频率测量仿真结果Table 2 Simulation results of main resonant frequency measurement in case 1

根据图5 和表2 可知，针对系统电容电流IC≤30 A 的谐振接地系统，为了满足技术条件的要求，在系统失谐度v=−5%时主谐振频率测量误差为0.35 Hz，即应该保证熄弧后的主谐振频率测量范围在50.87～51.57 Hz 内，与理论分析结果接近。

3.2 仿真验证2：系统电容电流30 AIC ≤100 A

仿真验证2 所用的谐振接地系统仿真结构如附录B 图B1 所示，根据表1 的分布参数，系统对地电容为Ctot，2，set=9.51 μF，对于10 kV 系统，系统电容电流为IC，2，set=51.73 A。

仿真验证流程与仿真验证1 相似，取消弧线圈电感L=338.12 mH（设定系统补偿度v=−5%），某次仿真试验的母线零序电压、消弧线圈电流和故障点残流波形如附录B 图B2 所示。

保持系统失谐度v=−5%不变，在此基础上逐渐改变配电网中的架空线或电缆的长度，使得系统对地电容电流分别取40、70、80、90 和100 A。重复以上仿真过程，主谐振频率fh与系统电容电流测量结果IC的关系如附录B 图B3 所示。表3 为仿真验证2 中系统电容电流不同时的主谐振频率测量仿真结果。

根据附录B 图B3 和表3 可知，针对系统电容电流30 AIC≤100 A 的谐振接地系统，为了满足技术条件的要求，在系统失谐度v=−5%时主谐振频率测量误差为0.23 Hz，即应该保证熄弧后的主谐振频率测量范围在50.99～51.45 Hz 内，而且不同配电网的主谐振频率测量范围要求近似相等，即此时的主谐振频率测量误差与系统电容电流的水平无关，与理论分析结果接近。

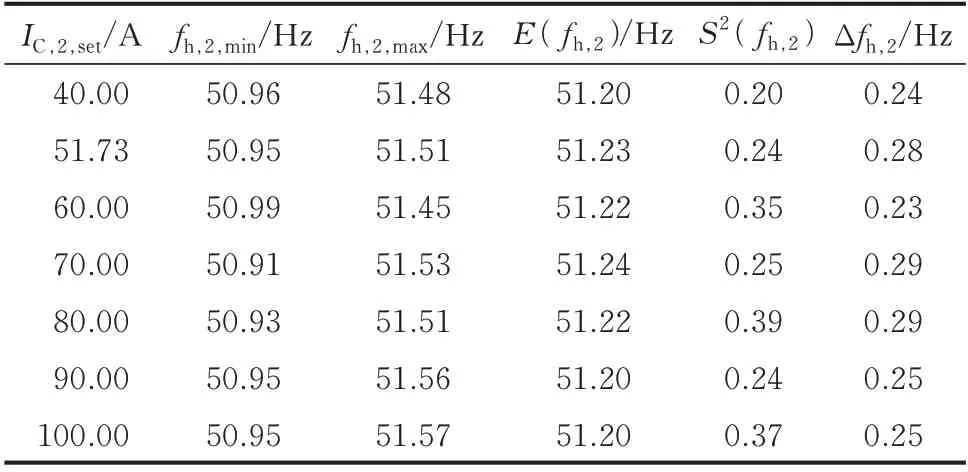
表3 仿真验证2 的主谐振频率测量仿真结果Table 3 Simulation results of main resonant frequency measurement in case 2

3.3 仿真验证3：系统电容电流100 AIC ≤150 A

仿真验证3 所用的谐振接地系统仿真结构如附录B 图B4 所示，根据表1 的分布参数，系统对地电容为Ctot，3，set=23.18 μF，对于10 kV 系统，系 统电容电流为IC，3，set=126.07 A。

仿真验证流程与仿真验证1 相似，取消弧线圈电感L=138.74 mH（设定系统补偿度v=−5%），某次仿真试验的母线零序电压、消弧线圈电流和故障点残流波形如附录B 图B5 所示。

保持系统失谐度v=−5%不变，在此基础上逐渐改变配电网中的架空线或电缆的长度，使得系统对地电容电流分别取110 和150 A。重复以上仿真过程，主谐振频率fh与系统电容电流测量结果IC的关系如附录B 图B6 所示。表4 为仿真验证3 中系统电容电流不同时的主谐振频率测量仿真结果。

表4 仿真验证3 的主谐振频率测量仿真结果Table 4 Simulation results of main resonant frequency measurement in case 3

根据附录B 图B6 和表4 可知，针对系统电容电流100 AIC≤150 A 的谐振接地系统，为了满足技术条件的要求，在系统失谐度v=−5%时主谐振频率测量误差为0.44 Hz，即应该保证熄弧后的主谐振频率测量范围在50.79～51.67 Hz 内，与理论分析结果接近。

3.4 仿真验证4：系统电容电流150 AIC ≤200 A

仿真验证4 所用的谐振接地系统仿真结构如附录B 图B7 所示，根据表1 的分布参数，系统对地电容 为Ctot，4，set=30.74 μF，对 于10 kV 系 统，系 统 电 容电流为IC，4，set=167.16 A。

仿真验证流程与仿真验证1 相似，取消弧线圈电感L=106.66 mH（设定系统补偿度v=−2%），某次仿真试验的母线零序电压、消弧线圈电流和故障点残流波形如附录B 图B8 所示。

保持系统失谐度v=−2%不变，在此基础上逐渐改变配电网中的架空线或电缆的长度，使得系统对地电容电流分别取180 A 和200 A。重复以上仿真过程，主谐振频率fh与系统电容电流测量结果IC的关系如附录B 图B9 所示。表5 为仿真验证4 中系统电容电流不同时的主谐振频率测量仿真结果。

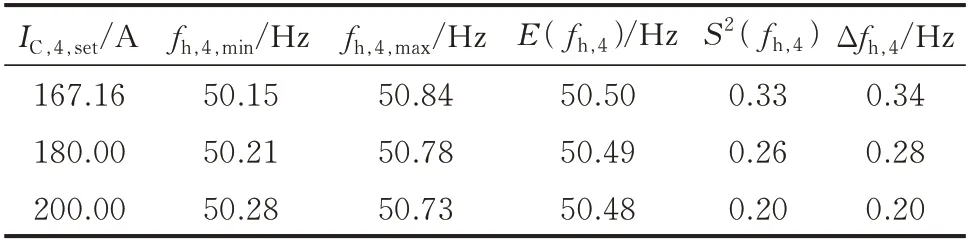
表5 仿真验证4 的主谐振频率测量仿真结果Table 5 Simulation results of main resonant frequency measurement in case 4

根据附录B 图B9 和表5 可知，针对系统电容电流150 AIC≤200 A 的谐振接地系统，为了满足技术条件的要求，在系统失谐度v=−2%时主谐振频率测量误差为0.20 Hz，即应该保证熄弧后的主谐振频率测量范围在50.28～50.68 Hz 内，与理论分析结果接近。

3.5 仿真验证5：过渡电阻对系统电容电流测量结果的影响

仿真验证5 采用附录B 图B1 所示谐振接地系统仿真结构，在保持消弧线圈电感值L=338.12 mH不变、设置发生单相接地故障时过渡电阻Rf∈(0，1 000]Ω 的情况下，进行1 000 次蒙特卡洛试验。仿真验证流程与仿真验证1 相似，值得注意的是，需要记录母线零序电压并进行消弧线圈电流的归算。某次仿真试验的母线零序电压、消弧线圈电流和故障点电流的波形如附录B 图B10 所示。

主谐振频率fh与系统电容电流测量结果IC的关系如附录B 图B11 所示。表6 为仿真验证5 和仿真验证2 中的主谐振频率测量仿真结果对比。其中:fh，min和fh，max分别为允许的主谐振频率测量下限和上限；E(fh)和S2(fh)分别为频率测量结果的数学期望和方差；Δfh为频率测量误差。

根据附录B 图B11 和表6 可知，针对系统电容电流IC=51.73 A 的谐振接地系统，在发生单相接地故障时过渡电阻Rf∈(0，1 000]Ω 的情况下，当系统失谐度v=−5% 时主谐振频率测量误差为0.24 Hz，即应该保证熄弧后的主谐振频率测量范围在51.01～51.49 Hz 内，与仿真验证2 中发生金属性接地时的主谐振频率测量误差相近，因此，发生单相接地故障时过渡电阻的大小并不影响该系统电容电流测量方法及其误差分析方法的适用性。

表6 主谐振频率测量仿真结果对比Table 6 Comparison of simulation results of main resonant frequency measurement

根据以上仿真验证结果可知，在系统结构不同或者过渡电阻不同的情况下，利用该主谐振频率测量误差分析方法得到的仿真结果与理论分析结论相符，均可以正确反映技术条件的测量要求。

4 结语

在谐振接地系统发生单相接地故障时，充分利用母线零序电压和消弧线圈电流等故障电气量，可以计算得到系统失谐度和系统电容电流等信息。在此过程中，通过分析主谐振频率测量误差，可以校验系统电容电流的测量结果。针对系统电容电流IC≤30 A、30 AIC≤100 A、100 AIC≤150 A 和150 AIC≤200 A 的4 种谐振接地系统，理想情况下主谐振频率最大测量允许误差分别为0.342、0.256、0.427 和0.189 Hz；考虑到现场运行情况，对于以上4 种情况，其主谐振频率最大测量允许误差分别为0.236、0.177、0.295 和0.133 Hz，因此建议统一取0.100 Hz。

本文分析中参考了现场运行经验，后续会进一步通过真型试验或现场数据进行全面验证，此外后续研究将根据本文给出的误差结果，设计高精度、高灵敏的暂态参数可靠提取方法，并量化现场各种因素对测量与提取方法的影响，从而使得基于熄弧前后暂态信息的系统电容电流测量方法落地实用。

该主谐振频率测量误差分析方法适用于不同系统失谐度和不同过渡电阻的情况，可迁移性较强。本文通过仿真验证，证明了该误差分析方法的有效性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。