直流微电网无界虚假数据注入网络攻击检测与系统恢复方法

郭方洪，郑祥康，邓 超，李 赫，余 为

（1. 浙江工业大学信息工程学院，浙江省 杭州市 310034；2. 南京邮电大学碳中和先进技术研究院，江苏省 南京市 210023；3. 格瓴新能源科技（杭州）有限公司，浙江省 杭州市 311422）

0 引言

微电网由分布式能源、储能系统和本地负荷组成［1］。与交流微电网相比，直流微电网的供电更为可靠、高效且不产生无功功率，因此直流微电网研究越来越受到关注［2］。直流微电网在孤岛运行模式下，常见的二层控制主要有集中式和分布式控制［3-4］。集中式控制需要一个强大的中央控制器来处理信息，并有实现成本高和容易单点故障等缺点［5］。因此，目前大多数二层控制策略采用分布式控制，通过构建一种引入邻居通信策略的二层控制器，将母线电压恢复至标称值，并实现各分布式电源（distributed generator，DG）间的电流分配［6］。

虽然分布式二层控制具有高效性和灵活性，但是其依赖于通信网络进行信息传输，易遭受网络攻击［7］。常见的网络攻击形式有拒绝服务（denial-ofservice，DoS）攻击［8］、重放攻击［9］和虚假数据注入（false data injection，FDI）攻击。其中FDI 攻击通过注入虚假数据而掩盖真实数据，进而影响直流微电网稳定运行，该攻击手段简单高效且具有迷惑性［10-11］。目前，对含FDI 攻击的微电网防御方法大致分为攻击检测和弹性控制两类。攻击检测方法通过观测系统运行状态对攻击进行实时监测；一旦检测到攻击立即对含攻击的相关信息进行隔离［12-14］。虽然该方法在一定程度上抑制了攻击的影响，但同时也隔离了有效信息，系统性能受到很大影响。另一方面，弹性控制方法则通过对攻击信号进行持续监测，设计一种攻击补偿策略实现系统性能恢复［15-19］。文献［15］提出了一种不依赖观测器的抵御常值攻击的分布式协同控制算法。而攻击者为躲避FDI 攻击检测，通常会设置时变攻击。目前，大部分研究均仅考虑有界时变攻击［16］。为满足攻击者最大化攻击危害的目的，攻击者通常将未知攻击信号设置为一种更具一般性的无界攻击形式。文献［17］采用分布式虚拟弹性层（virtual resilient layer）技术首次对无界攻击展开研究，但该方法需假设该虚拟弹性层不遭受攻击。针对虚拟弹性层受到攻击的情况，文献［18-19］设计了一类将虚拟弹性层与脆弱的网络物理层互连的完全分布式弹性控制方法，可以有效应对网络物理层和虚拟弹性层同时受到未知无界FDI 攻击的情况。综上所述，针对FDI 攻击，现有大多数文献只单独考虑攻击检测或弹性控制设计，如何发挥上述两种策略各自的优点，设计一种集成攻击检测与弹性控制方法还有待进一步研究。此外，针对无界FDI 攻击，现有的弹性控制方法均采用了基于分布式通信的虚拟弹性层，如何设计一种不依赖通信的分散式弹性控制方法也值得进一步探索。

基于上述讨论，针对现有分布式二层控制的通信信道可能发生网络攻击的情况［20］，本文将研究无界FDI 攻击下的直流微电网电流分配和电压恢复问题，提出一种集攻击检测与系统恢复于一体的控制方法。本文主要贡献如下:1）针对直流微电网无界FDI 攻击的防御问题，结合攻击检测与弹性控制各自优点，提出了一种集攻击检测与系统恢复方法于一体的防御策略；2）不同于现有分布式弹性控制方法，提出了一种无需邻居信息交互的分散式弹性控制方法，并从理论上严格证明了该方法的稳定性。最后，通过多个仿真案例验证了所提方法的有效性。

1 基于分布式二层控制的直流微电网系统模型

本文考虑的直流微电网系统主要包括N个DG和M个负荷，以并联的形式连接在一个公共的直流母线上，如图1 所示。各个DG 的一层控制主要由下垂控制、电压环和电流环组成。首先介绍基于下垂控制的一层控制策略，然后对分布式二层控制模型进行简要分析，并指出该模型存在的局限性。

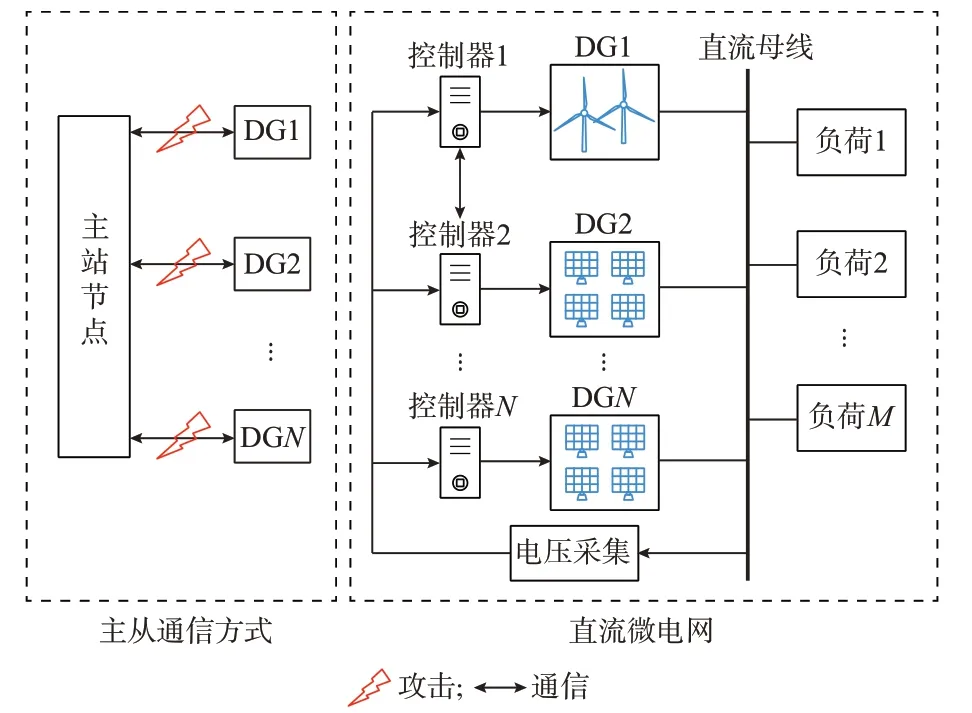
图1 直流微电网及通信方式Fig.1 DC microgrid and communication mode

1.1 下垂控制

为了保证直流微电网的稳定运行，通常使用下垂控制来实现DG 间的电流分配。直流微电网中第i个DG 的下垂方程可表示为［21］:

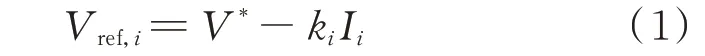
式 中:Vref，i为 参 考 电 压；V*为 电 压 标 称 值；ki为 下 垂系 数；Ii为 第i个DG 的 输 出 电 流。

由于该电网中所有DG 均连接在同一直流母线上，故该母线电压Vb可表示为:

式中:Vi和Ri分别为第i个DG 的输出电压和传输线电阻。

文献［22］研究表明，通过选择合适的电压与电流控制环的参数，第i个DG 的输出电压Vi能快速跟 踪 到 其 参 考 电 压Vref，i，即Vi=Vref，i。结 合 式（1）和式（2），进一步可得母线电压Vb为:

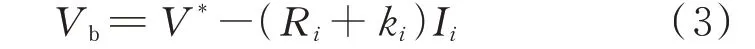
由式（3）可知，各DG 间的输出电流分配比为:

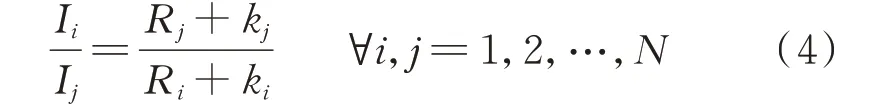
当选取的下垂系数ki远大于传输线电阻Ri时，即ki≫Ri，则电流分配精度仅与下垂系数有关，即

式（5）表明，下垂系数ki越大，电流分配精度越高。然而由式（3）可知，下垂系数ki越大，母线电压与标称电压的偏差也越大。因此，在传统的下垂控制中需选取合适的ki，在保证电流分配精度的同时，尽可能减小电压偏差［23］。

1.2 分布式二层控制模型

为解决一层控制中电流分配精度和母线电压波动之间的矛盾，研究者提出加入二层控制以修正一层控制的工作点，平移下垂曲线。其具体做法是在一层控制式（3）中加入二层控制信号ui，即

定义母线电压误差eV和控制输入一致性误差eui为:

式中:Ni为第i个二层控制器的邻居集合。

在式（7）的基础上，文献［22］提出的分布式二层控制器可表达为:

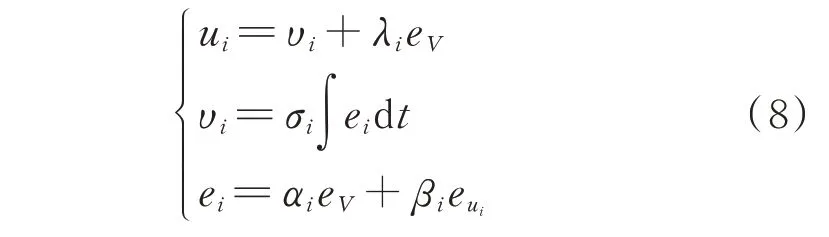
式中:λi，αi，βi∈R+为误差增益；σi为积分控制系数。

该分布式二层控制器既解决了母线电压偏差问题，也保证了下垂控制的电流分配精度，有

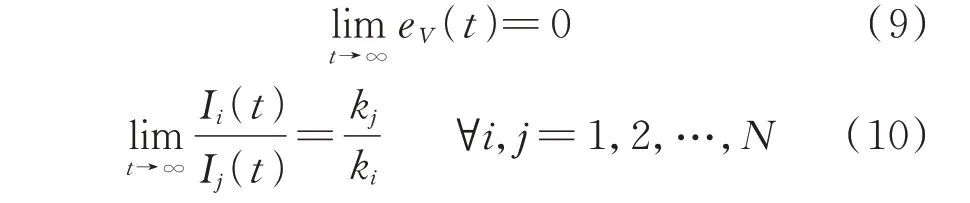
为实现上述目标式（9）、式（10），分布式二层控制器式（8）需要各个DG 间的信息交互和通信。需要指出，当所有DG 均采用下垂控制策略实现电流分配时，所有DG 的地位是对等的。该种对等控制方式不需要领导者，具有可拓展性和可靠性高等优点。此外，特别需要注意的是，对等控制并不等于对等通信。在实际过程中，邻居间的通信信号并不一定直接传输，也可以通过主从通信方式进行信息交互。如图1 所示，此控制方式极易遭受网络攻击，当攻击者在系统中寻找漏洞并对直流微电网进行FDI攻击时，此控制器将不能完成相应的控制目标，甚至整个系统的稳定性将遭到严重破坏［15］。针对上述问题，如何对二层控制器式（8）进行改进，提出一种能够实时监测并抵御FDI 攻击的二层控制策略是本文的研究重点。

2 攻击检测模块与弹性控制器设计

本章将在上文所述分布式二层控制的基础上，考虑FDI 攻击对其影响，建立FDI 攻击模型、设计攻击检测模块、研究能够实现系统恢复的弹性控制策略。

2.1 攻击模型

本文考虑分布式二层控制器式（8）中邻居间的信息交互通道遭受FDI 攻击，即在原二层控制器接收到的邻居控制信号uj的基础上叠加未知FDI 攻击信号γj。上述攻击模型可表示为:

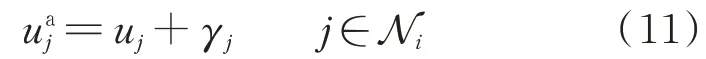
为了便于理论研究，对该FDI 攻击信号做如下假设。

假设1:假设攻击信号γj一阶导数有界［24］，即|γ̇j|≤dj，且dj∈R+。

需要指出的是，假设1 只要求注入的攻击信号的导数有界，而对其幅值并无限制，即该攻击信号本身可以是无界的。这与文献［16］和文献［25］考虑的有界FDI 攻击相比，更符合实际场景。当然，该假设对相应的弹性控制器设计提出了更严苛的要求。

考虑攻击模型式（11），分布式二层控制器式（8）的输出可表示为:

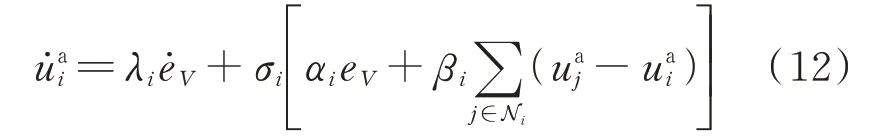
显然，若将该控制输出加入一层控制中，将会影响控制目标式（9）、式（10）的实现，甚至导致系统的不稳定。换而言之，攻击者加入FDI 攻击会影响电压与电流的稳定，以实现相应的攻击利益（如使得攻击方经济效益最大化等），这将带来系统运行和用户用电的安全问题［26］。

为此，针对式（11）中的无界FDI 攻击，本文提出一种集攻击检测和系统性能恢复于一体的控制策略，相应的整体控制框图如图2 所示。其核心思想是:1）通过设计一种基于残差评估函数的攻击检测模块，实现对通信网络可能存在的FDI 攻击进行实时检测；2）若不存在FDI 攻击，则二层控制仍然按照原控制器式（8）进行输出；3）若检测到FDI 攻击，则启动相应的弹性控制器，对原控制器的输出进行修正，以期抵御FDI 攻击，并能实现原控制目标式（9）、式（10）。

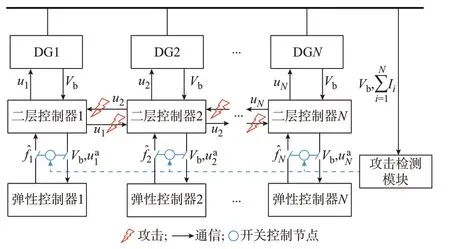
图2 本文所提方法控制框图Fig.2 Control block diagram of proposed method

2.2 攻击检测模块

如文献［16］所述的传统FDI 攻击主要考虑对物理层的量测信号进行篡改，然而在通常情况下，攻击者很难篡改量测信号。与该问题不同，在分布式通信架构下，网络层的控制信号更易遭受FDI 攻击，因此需设计新的攻击检测方案。此外，网络层的FDI攻击可以改变电流分配比例、影响电压稳定，而正常的系统负荷波动等因素也会引起电压与电流波动。如何区分FDI 攻击和其他正常系统影响因素是该攻击检测模块设计的难点之一。下面给出攻击检测模块的设计过程。

首先，将式（8）代入式（6）可得:

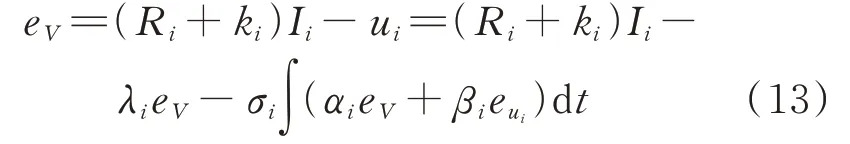
对式（13）两边同除Ri+ki，可得输出电流Ii为:

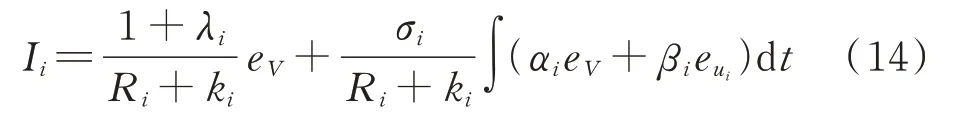
取控制器参数βi=ι(Ri+ki)，∀i=1，2，…，N，其中ι为调节参数。可得总输出电流为:

由式（15）可知，系统总输出电流仅与电压偏差eV有关。若系统的通信层遭受FDI 攻击，该等式关系将不成立。基于此，定义残差评估函数J为:

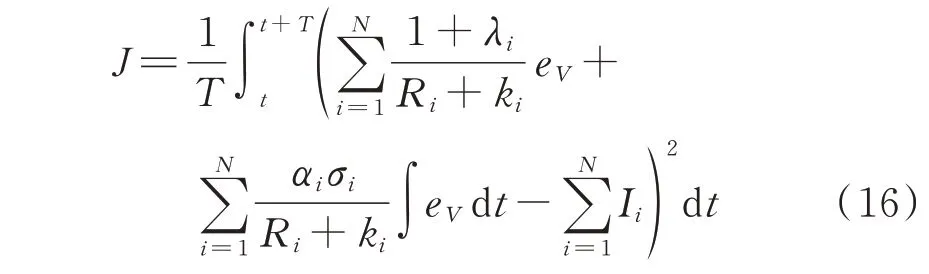
式中:T为评估函数有限时间窗口。

理论上，若系统未遭受FDI 攻击，式（16）中的函数值为0。但实际系统中会存在一定的量测噪声，为在提升检测速度和降低误报率之间取得折中，根据文献［27］，本文在无攻击情况下，选择如下检测阈值Jˉ:

式中:sup(·)为取上限函数。

若式（16）中的评估函数值J大于该阈值Jˉ，则表明二层控制的通信网络存在FDI 攻击；否则认为直流微电网系统未受到攻击。

需要指出，在式（16）的评估函数中，只使用了系统的物理信号输出（母线电压和总负荷电流），并未使用到任何邻居间的交互信息，因此该检测模块本身不会受FDI 攻击信号的影响。相比文献［27］，本文的攻击检测模块设计更具合理性。

2.3 基于弹性控制器的系统恢复方法研究

考虑FDI 攻击模型式（11），在式（12）的基础上，定义中间变量fi，用来刻画该攻击对原控制器的影响，即

将式（18）与式（8）相减可得:

将式（11）、式（20）代入式（19）可得:

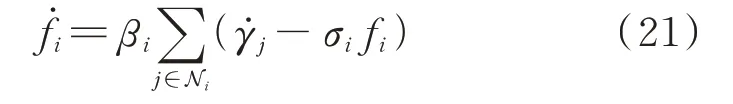
式（21）建立了攻击信号γj的导数与中间变量fi的关系，这给接下来对攻击信号γj的估计提供了基础。此外，式（21）中只包含攻击信号的导数信息，并不包含攻击信号本身，因此成功解决了无界FDI攻击信号估计问题。

从式（18）可知，若能够实时观测中间变量fi的大小，并将其补偿到原二层控制输入中，将实现无界FDI 攻击下的弹性控制。

为此，针对中间变量fi，受文献［28］启发，本文设计如下二阶分散式滑模观测器:

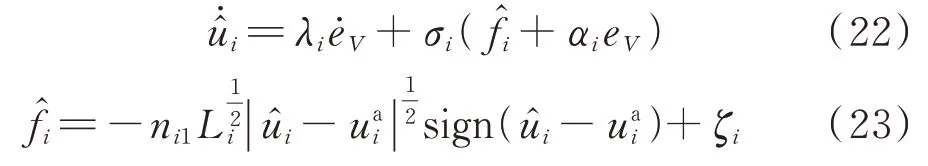
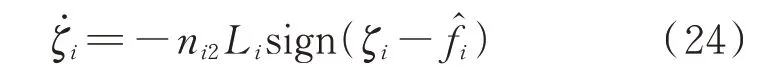
式 中:ûi、f̂i分 别 为、fi的 观 测 信 号；ni1、ni2、Li∈R+均为第i个DG 的观测器参数；ζi为中间变量；sgn(x)为式（25）所示的符号函数。

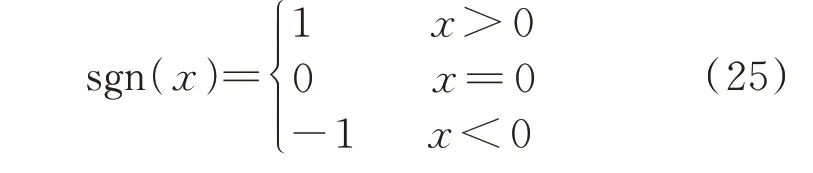
值得指出的是，该观测器是一个有限时间观测器，其不仅具有响应速度快、瞬态性能好等特点，而且对外界干扰具有较强的鲁棒性［29］。此外，该观测器仅需要本地信息，并不需要邻居的通信信息。因此与文献［17-19］所提方法相比更具鲁棒性和经济性。

最后，将该观测信号f̂i补偿至受攻击的二层控制器式（18）中，可得弹性控制策略下的二层控制恢复信号满足:

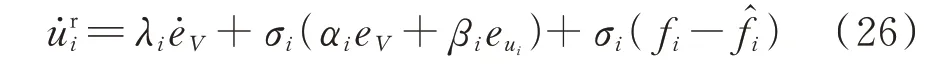
利用本文所提的攻击检测和系统恢复策略，受攻击时DGi的控制框图如图3 所示。图中，PWM 为脉宽调制。

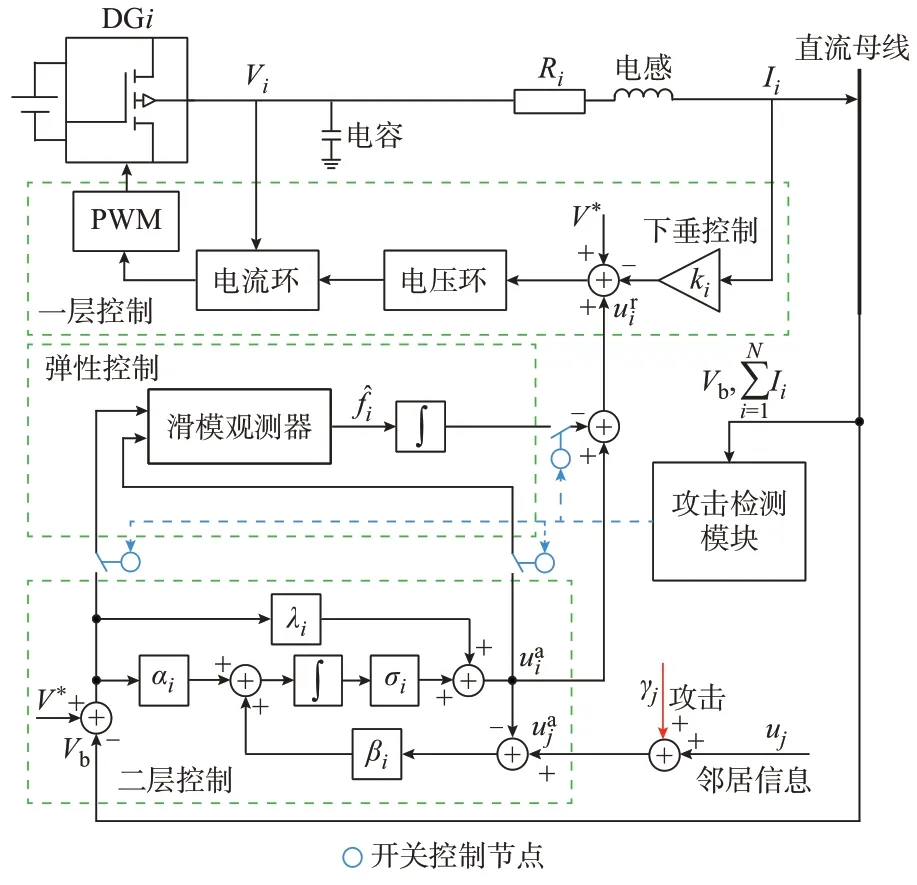
图3 受攻击时DGi 的控制框图Fig.3 Control block diagram of DGi under attack

由图3 可知，第i个DG 的弹性控制器仅需获取受攻击的二层控制输出和母线电压Vb信息，而不需要邻居信息uj作为弹性控制器输入。通过对中间变 量fi进 行 观 测，得 到 观 测 信 号，再 将̂ 作 为 补 偿信号叠加到原二层控制输出中，以抵消无界FDI 攻击的影响，并使该系统即使在无界FDI 攻击下仍然保证电流精确分配和母线电压的二次恢复。本文总结所提弹性控制器的有效性以及系统的稳定性，提出定理1。

定理1:考虑无界FDI 攻击模型式（11），直流微电网分布式二层控制器式（8）在弹性控制策略式（22）至式（26）的补偿下，仍可实现电流分配和电压恢复的目标式（9）、式（10）。

证明:首先，定义第i个DG 的第1 个中间变量φi1和第2 个中间变量φi2为:

由式（27）和式（28）可得:

结合式（18）与式（29）可知:

将式（22）代入式（30）可得:

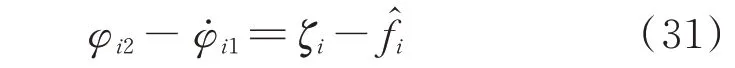
进一步，联立式（22）至式（24）可得:

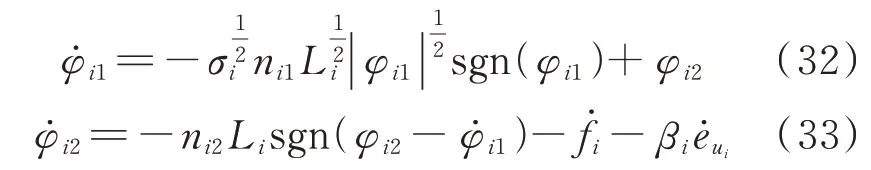
由式（21）可推得:

显 然 在 有 限 时 间 内ḟi和βiėui均 是 有 界 的，选 取观测器参数Li满足:

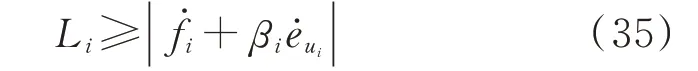
则式（33）可写为如下形式:

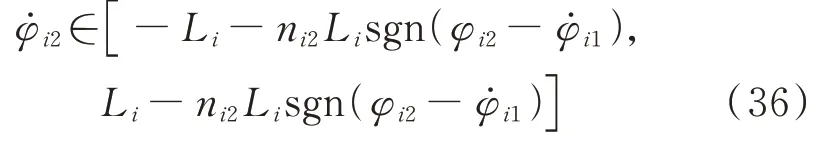
根据式（32）与式（36），进一步推导可得在有限时间内［30］，有

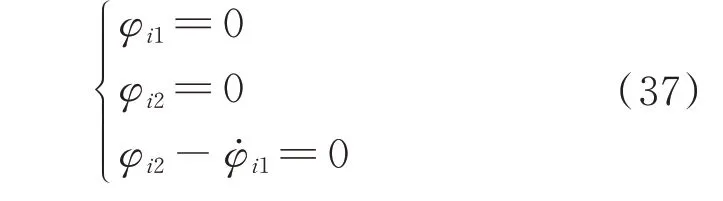
由式（37）可知，存在时间T1>0，使得当t>T1时，有

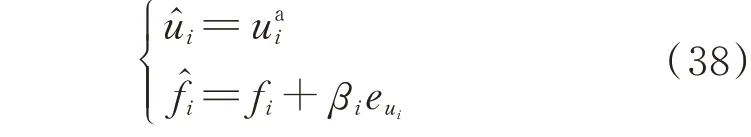
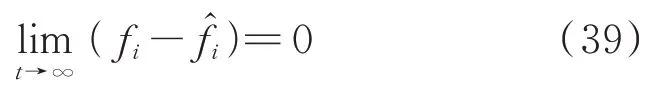
式（39）表明观测信号f̂i能跟踪到中间变量fi，并结合式（8）与式（26）进一步可得，二层控制恢复信号可以恢复至原二层控制信号ui，即

式（40）表明攻击者发起FDI 攻击后，使用所提方法对攻击进行补偿，最终二层弹性控制系统可以消除攻击的影响，实现电流的精确分配（式（10））与母线电压的恢复（式（9））。

3 仿真验证分析

为进一步验证所提方法的有效性，基于MATLAB/Simulink 搭建了一个含有4 个DG 的直流微电网仿真模型。其中包括3 个常规DG（DG1、DG2 和DG3）、1 个 备 用DG（DG4）和2 个 负 荷（RL1=5 Ω，RL2=10 Ω）。本仿真模型详细参数配置和攻击信号如附录A 表A1 和表A2 所示，其中，t1、t2分别表示攻击1 与攻击2 的发生时间。攻击下不同方法的控制性能对比如图4 所示。

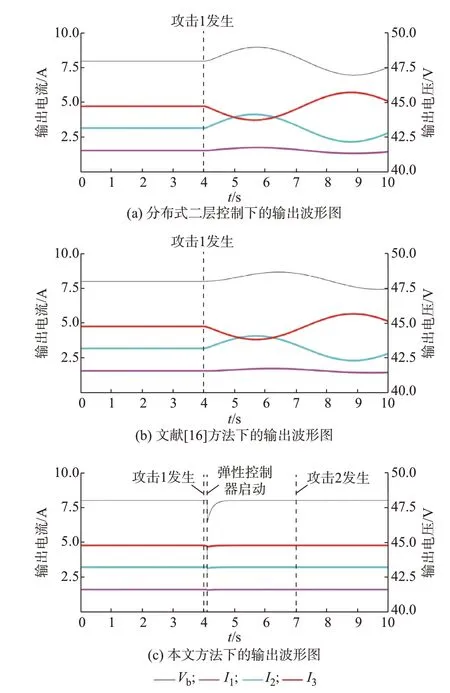
图4 攻击下不同方法的控制性能对比Fig.4 Comparison of control performance of different methods under attack

案例1:验证攻击下二层控制器式（8）的控制性能。在分布式二层控制方法下，负荷端仅连接负荷RL1，电流按I1∶I2∶I3=1∶2∶3 的比例进行分配。由图4（a）可知，假设第4 s 发生FDI 攻击1，电流和电压均产生了较大的波动，即分布式协同控制不再有效，电流不再按比例分配，母线电压的稳定性也遭到破坏。由此可知， FDI 攻击将使传统的分布式二层控制方法失效。

案例2:验证攻击下文献［16］方法的控制性能。在文献［16］的弹性控制方法下，电流按I1∶I2∶I3=1∶2∶3 的比例进行分配。如图4（b）所示，假设第4 s 发生FDI 攻击1，即使该方法对FDI 攻击持续监测，在第4 s 后的电压与电流仍然产生了巨大的波动，可以看出该方法无法抵御本文所考虑的无界FDI 攻击。

案例3:验证攻击下本文所提出方法的控制性能。如图4（c）所示，假设第4 s 发生攻击1，攻击检测模块在4.1 s 检测出攻击，自动开启观测器抵御FDI 攻击。在4.8 s 时，电压恢复至48 V，输出电流仍按I1∶I2∶I3=1∶2∶3 比例分配，这意味着攻击1 产生的影响已被弹性控制器消除。假设第7 s发生攻击2，在弹性控制器的持续监测下，电流和电压均没有明显波动，体现了所设计弹性控制器具有响应速度快、瞬态性能好等特点。本案例验证了本文所提出方法的有效性。

案例4:验证不同攻击下本文所提出方法的性能。案例3 中的攻击1 和攻击2 是分时发生的，本案例将考虑攻击1 与攻击2 同时发生的情况，进一步验证本文所提方法的有效性。如图5（a）所示，在分布式二层控制下，假设第5 s 同时发生攻击1 和攻击2，攻击检测模块在5.1 s 检测出攻击后，启动观测器抵御FDI 攻击。在5.8 s 时攻击被消除，电流继续按I1∶I2∶I3=1∶2∶3 的比例分配，母线电压仍然维持在标称值48 V。攻击1 与攻击2 的同时发生意味着所有的控制器接收到的信号均同时受到攻击，在该情况下，本文所提出方法仍然具有有效性。

案例5:验证负荷和备用DG 接入下本文所提出方法的性能。本案例将在FDI 攻击环境下，改变负荷条件以及验证DG 的即插即用功能。如图5（b）所示，在攻击1 与攻击2 下，考虑第3 s 改变负荷条件，将负荷RL2接到直流母线上，电流值改变，而电流比例仍按I1∶I2∶I3=1∶2∶3 分配。假设第6 s 将DG4 接到直流母线上，母线电压经小幅波动后恢复到标称值48 V。而由于备用DG 的接入，电流值再次改变，但仍按I1∶I2∶I3∶I4=1∶2∶3∶3 预先设定的比例分配。仿真结果表明，本文所提出的方法具有较强的鲁棒性。

图5 不同条件下的弹性控制性能Fig.5 Resilient control performance under different conditions

4 结语

本文针对无界FDI 攻击下的直流微电网二层控制系统，研究其电流分配和电压恢复问题。首先，基于残差评估函数设计了攻击检测方法；其次，基于分散式滑模观测器设计了弹性控制器，最终实现了FDI 攻击下的电流分配及电压恢复；最后，在微电网系统中进行了仿真验证，其结果表明，本文所提出的集攻击检测与系统恢复方法于一体的防御策略可以抵御任意通信信道发生的无界FDI 攻击，该策略在有效性和鲁棒性方面均取得了良好的表现。

本文所提出的方法能有效消除无界FDI 攻击的影响，但仍存在着诸如无法抵御DoS 攻击和未考虑并网运行模式下攻击的不足。此外，如何在同时考虑控制器攻击与测量系统攻击两种攻击形式下的弹性控制策略的设计，是一个值得研究但颇具挑战性的工作。

感谢南京邮电大学科研启动基金(NY221007)对本文工作的支持！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。