基于SRCKF 的多传感器融合自适应鲁棒算法

2023-02-09李春辉马健杨永建肖冰松邓有为

北京航空航天大学学报 2023年1期

李春辉，马健，杨永建，肖冰松，邓有为

(空军工程大学航空工程学院，西安 710038)

容积卡尔曼滤波[1-2]（cubature Kalman filter，CKF）是Arasaratnam 等学者提出的一种非线性滤波算法。CKF 基于三阶球面径向原则进行数值运算，逼近最优滤波框架中的状态后验分布[3]，能以至少二阶泰勒精度逼近任何非线性系统的后验协方差和均值[4]，在目标跟踪[5]、导航[6]等领域应用广泛。为了获得更高的数值稳定性，正交三角分解被引入CKF 迭代过程，构成了平方根CKF（square-root CKF，SRCKF）算法。

但是，CKF/SRCKF 算法的自适应性和鲁棒性并不总能满足实际应用场景的需求，如机动目标的跟踪。从滤波的角度出发，影响SRCKF 状态估计性能的主要因素有2 类：①目标建模与实际不匹配、目标机动后状态发生突变等造成的模型误差；②量测缺失、量测偏差等造成的异常量测值[7]。

目前，主要有2 种途径克服模型误差：①从提高模型自适应性和准确性出发对目标进行再建模[8-10]；②构建和改进各种自适应滤波算法[11-13]。其中，SRCKF 与强跟踪滤波器（strong tracking filter，STF）架构的结合可以有效克服模型误差的影响[14-17]，但是也存在求解计算量大[17]等局限，因此，文献[18]提出了基于新息修正的低复杂度自适应CKF（low complexity adaptive cubature Kalman filter, LCACKF）算法，可以作为STF 的有效替代算法。另外，针对异常量测值也有各种鲁棒技术[19-21]。但是上述方法难以克服模型误差和异常量测值同时发生带来的不良影响。

实际上，也有一些鲁棒滤波器可以解决上述问题，如鲁棒M-M 滤波器[22]、H∞滤波器[23]和重尾分布噪声滤波器[24-25]等。但是这些滤波算法存在理论推导复杂、迭代次数多的局限性。此外，构建自适应鲁棒滤波器[26-30]也可以有效克服这一问题。Yang 等[26-27]建立了一套自适应鲁棒卡尔曼滤波（adaptively robust Kalman filter, ARKF）理论，利用鲁棒估计方法控制测量异常值，并引入自适应渐消因子克服模型误差，成功运用于动态导航定位[28]。但是当在无法获得全局状态的鲁棒估计解时，ARKF就可能失效[29]，因此文献[30]基于ARKF 架构提出了一种鲁棒多渐消因子容积卡尔曼滤波（robust multiple fading factors cubature Kalman filter, RMCKF），克服了ARKF 的局限性，且迭代次数少。RMCKF结合了STF 架构及基于Huber 函数的鲁棒估计，但是RMCKF 为次优算法的结合，滤波精度不够高，而且当新息出现较大偏差时，均是基于新息构建的渐消因子和修正的量测误差协方差矩阵就难以正确有效的获得。

因此，为了克服模型误差和异常量测值的影响，一方面受到自适应鲁棒滤波器结构的启发，另一方面结合多传感器信息融合技术精度高和互补性强等优点[31]，本文提出一种多传感器融合自适应鲁棒算法。首先，基于新息协方差匹配原则设计了鲁棒子系统以控制异常量测值；然后，将文献[18]中提出的自适应算法与SRCKF 结合构成LCASRCKF，并用其代替STF 设计了自适应子系统，以此克服模型误差；最后，结合2 种子系统的特点和算法设计缺陷提出了一种基于分布式的融合架构，使得全局输出可以充分平衡并利用先验的模型预测值信息和后验的量测值信息。仿真结果验证了本文所提融合架构和融合算法的有效性，在存在模型误差和异常量测值的情况下，融合算法有着明显更优的状态估计性能。

1 平方根容积卡尔曼滤波

考虑如下非线性离散加性噪声系统：

式中：f( )和h( )分别为非线性状态转移函数和量测函数；xk+1和zk+1分别为n维和l维的状态向量和量测向量；wk和vk+1分别为过程噪声和量测噪声，两者相互独立且对应的噪声协方差矩阵分别为Qk和Rk+1，均为高斯白噪声。

对于式（1）和式（2）所建模的系统，假设k时刻系统的状态估计值xˆk|k和估计误差协方差Pk|k已知，则SRCKF 算法在k+1时刻的状态估计步骤可以总结如1.1 节、1.2 节所示。

1.1 时间更新

1）使用k时刻状态估计值xˆk|k和估计误差协方差Pk|k估计容积点：

1.2 量测更新

2 子系统设计与融合架构

2.1 基于新息协方差匹配的鲁棒SRCKF 子系统

对于多传感器融合算法，子系统的鲁棒性是保证系统整体性能的关键因素。如果子系统对异常量测值不具有鲁棒性且不能及时识别和隔离误差，融合效果就会产生偏差甚至发散。因此，文献[7,32]都是先设计鲁棒滤波算法，再对全局融合进行设计。

协方差匹配原则是一种理论简单且计算量小的鲁棒技术[12]，可以通过对量测噪声进行修正和调整，以此削弱异常量测值在滤波过程中的作用。因此，基于新息协方差匹配来建立鲁棒SRCKF 子系统。当系统滤波正常时，理论和实际的新息协方差矩阵相匹配：

实际上，鲁棒算法应该在异常量测值存在的情况下再去影响滤波器特性，否则就会对滤波最优性造成影响。因此需要建立切换准则，根据数据实际情况来选择标准或者鲁棒SRCKF。基于假设检验理论建立的服从 χ2分布的质量检测统计函数是一种有效的方法[8-9,17]，但是随着量测向量维数的增加，统计函数的计算负载也随之增大，实时性会受到影响。

基于门限判决的切换准则和基于 χ2分布的质量检测统计函数实质上都是概率论的运用，两者的容错率都可以得到保证。

2.2 基于修正的自适应SRCKF 子系统

目标机动或者目标建模不匹配造成的模型误差也会使得滤波器性能下降甚至滤波发散，这是因为之前的数据在滤波过程中起到了过强的牵制作用[33]，需要加强新的量测数据的作用来使系统及时跟踪真值。当模型误差存在时，状态预测值就会与真实目标状态产生偏差，进而使新息增大。从式（20）可以看到，若子系统仍然运行鲁棒SRCKF 算法，修正后的Rk+1会增大，反而导致量测信息在滤波过程中比重进一步减小。显然，算法设计的基本思想导致鲁棒子系统难以克服模型误差。

这就需要设计自适应子系统来解决这一问题。LCACKF 算法通过设置与新息关联的判定门限和修正准则，直接对状态预测值xˆk+1|k进行修正，使得预测值可以及时“跟上”目标真实状态，减小预测误差，进而减小状态估计误差[18]。文献[18]通过误差分析和仿真验证表明该算法不仅有较高的滤波精度，还具有低算法复杂度和快速收敛等优势，将其与SRCKF 结合构成LCASRCKF 后可以作为STF-SRCKF 的有效替代算法，用以克服模型误差带来的不良影响。但是该算法还存在一些问题，需要改进。

文献[18]中对修正判决门限的设置基于经验和具体仿真场景。本文将判决门限缩放因子 λ区间调整为[2,3)，调整结合了设计鲁棒系统时用到的3σ准则。之所以比3 稍小一些是为了增加修正区域对模型误差的敏感性，减小滤波过程中积累误差的影响。

LCASRCKF 算法并不能有效控制异常量测值，这也是由算法设计的基本思想造成的：对于状态预测值的修正是基于新息的，当新息偏差源自异常量测值而非目标状态的突变时，新息就不能反映出预测值偏离实际状态的趋势，此时再使用修正算法反而会进一步增大预测误差。实际上，这也是很多克服模型误差的自适应算法都有的缺陷，如STF 通过实时调整增益矩阵，加重量测数据在滤波中的作用，可以有效克服模型误差，但是在异常量测值出现时其滤波性能显然会受到较大影响。

2.3 融合准则和融合架构

由上述分析可知，单独的自适应子系统和鲁棒子系统难以同时克服模型误差和异常量测值的影响，这是2 种算法设计时的基本思想造成的，也就使得直接进行简单的量测融合或者状态融合并不能达到预期的效果和精度。因此，本文中对融合架构进行改进，主要考虑以下几点因素：

1）鲁棒SRCKF 子系统的鲁棒量测值和高量测精度是自适应SRCKF 子系统所需要的。

2）对于自适应SRCKF 子系统，修正后的状态预测值贴近目标真实状态，一方面可以为全局融合提供更多信息，另一方面也是难以自适应跟随目标状态变化的鲁棒SRCKF 子系统所需要的。

通过设计一种基于分布式的融合架构可以实现：在所有系统滤波正常时，融合使用了更多的信息，因此全局输出的精度会明显提升；当存在模型误差和量测偏差时，通过融合使得全局输出可以有效充分地利用先验的模型信息和后验的量测信息；当突变型不良量测甚至量测缺失的情况出现时，可以避免自适应子系统对全局输出的“抵消”作用。

3 数值仿真与分析

3.1 仿真条件设置

融合系统由1 个高量测精度的鲁棒SRCKF 子系统和2 个自适应SRCKF 子系统组成，按照图1中的架构进行融合输出。在滤波过程中，3 个子系统的过程噪声协方差矩阵均为Q=diag(1,1,1,1)，鲁棒子系统和自适应子系统的量测噪声协方差矩阵分别为RR= diag(50,50)，RA=diag(100,100)。

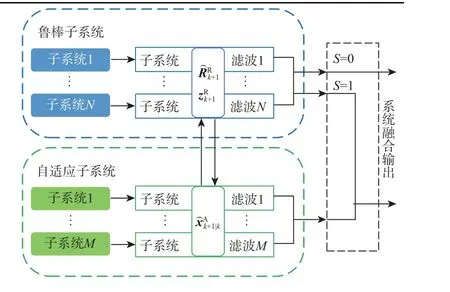
图1 融合架构Fig. 1 Fusion architecture

为验证本文所提融合算法在模型误差和异常量测值存在时的有效性，将本文算法与SRCKF 算法、LCASRCKF 算法、RMCKF 算法进行对比。融合算法中的门限调节参数 β为9，同时为了对比有效，LCASRCKF 和RMCKF 所使用的量测噪声协方差矩阵也设置为RR。

使用x和y方向上的位置均方根误差（root mean square error, RMSE）对滤波算法的状态估计性能进行量化评价，并进行200 次蒙特卡罗实验，得到统计平均结果，RMSE 通过式（32）计算：

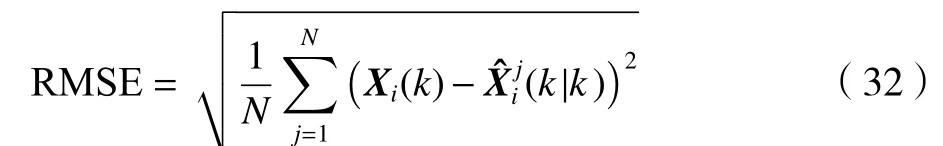
式中：N为仿真总次数；j和k指第j次仿真的k时刻；Xi(k) 和Xˆij(k|k) 分别为状态向量第i维分量的真实值和状态估计值。每次蒙特卡罗仿真中，滤波初始值和目标初始状态保持一致。

3.2 仿真场景1：模型误差

在仿真场景1 中，4 种算法在滤波过程中均一直使用FCV，以此在30～60 s 及90～120 s 两个时间段引入由于模型不匹配造成的模型误差；其次在80 s 时引入[0，30 m/s，0，30 m/s]T的速度突变，以此引入由于状态突变造成的模型误差。其中一次仿真的目标真实轨迹及4 种算法的滤波轨迹如图2 所示。可以看出，4 种算法都能跟踪目标实际运动，但是目标2 次转弯阶段即存在模型不匹配时，SRCKF 算法性能下降，估计出的轨迹和真实轨迹不能很好契合。

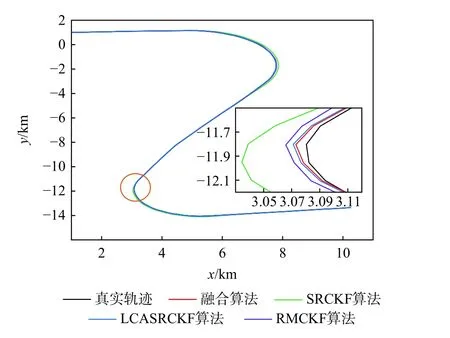
图2 目标运动轨迹（场景1）Fig. 2 Target trajectory (scenario 1)

4 种算法在x和y方向上位置的RMSE 曲线对比如图3 和图4 所示，对应的平均RMSE 值如表1所示。

从图3 和图4 可以看出，在模型准确的情况下，本文所提融合算法的滤波精度明显高于其他3 种算法，而由于RMCKF 和LCASRCKF 都是次优算法，量测精度比SRCKF 算法还要差一些。另外，在模型不匹配和状态突变造成模型误差时，SRCKF算法的RMSE 曲线会发生较大跳变，RMCKF 和LCASRCKF 算法都能克服模型误差的不良影响，值得注意的是，RMCKF 算法精度低于LCASRCKF 算法，这是因为此时偏差的主要来源是模型误差，RMCKF-算法对Rk+1的鲁棒修正会对渐消因子的作用产生一定的“削弱”。

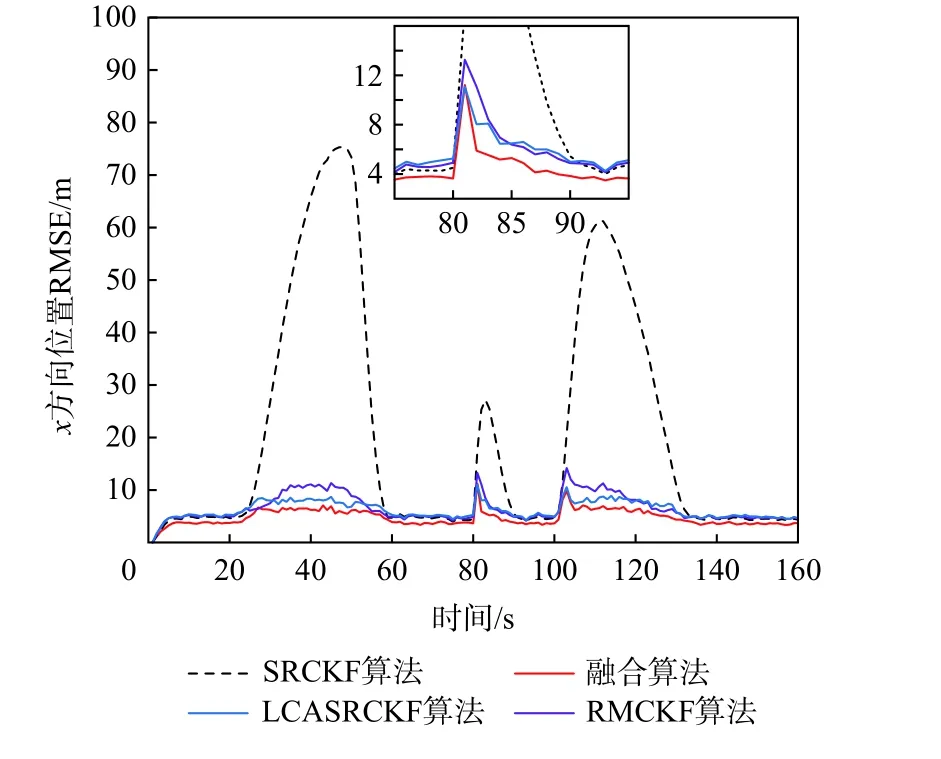
图3 x 方向位置均方根误差（场景1）Fig. 3 RMSE of position in x axis (scenario 1)

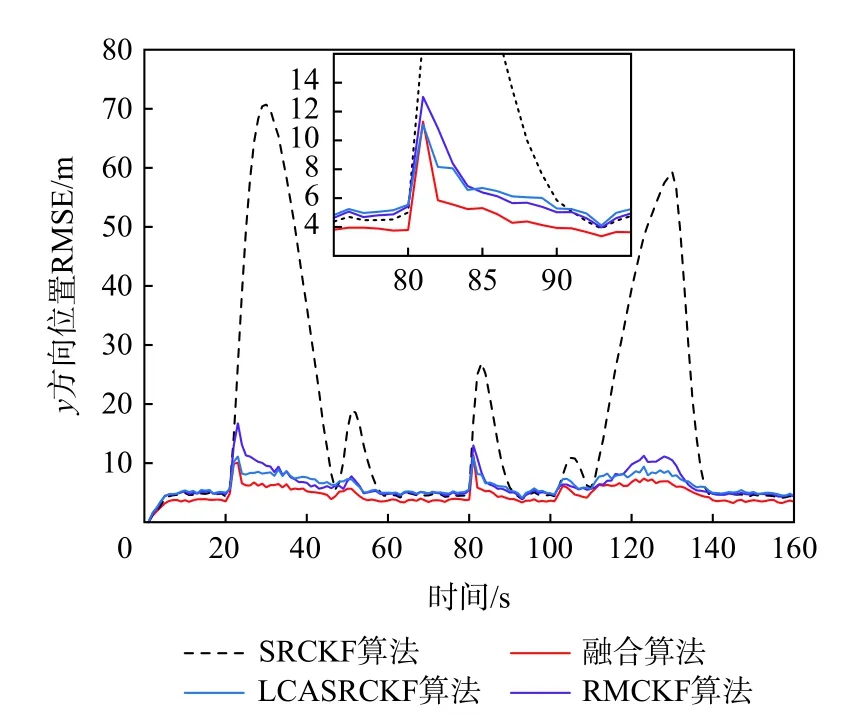
图4 y 方向位置均方根误差（场景1）Fig. 4 RMSE of position in y axis (scenario 1)

结合表1 可以看到，融合算法有着明显更优的滤波精度和收敛速度，这是因为融合架构中不仅包含更多鲁棒子系统的量测信息，还融入了更多自适应子系统修正后的状态预测信息。

表1 平均RMSE 对比（场景1）Table 1 Comparison of mean RMSEs (scenario 1)

3.3 仿真场景2：异常量测值

在场景2 中，模型误差（同场景1）及异常量测值同时发生。将10 ～12 s 的量测值置零以引入量测缺失的情况，同时对80 s 和105 s 的量测值分别引入[400 m，400 m/s，400 m，400 m]T和[300 m，300 m/s，300 m，300 m]T的量测偏差。

4 种算法在x和y方向上的位置RMSE 曲线对比如图5 和图6 所示，图7 和图8 为对应RMSE 曲线的放大图；表2 为4 种算法平均RMSE 值的对比。

表2 平均RMSE 对比（场景2）Table 2 Comparison of mean RMSEs (scenario 2)

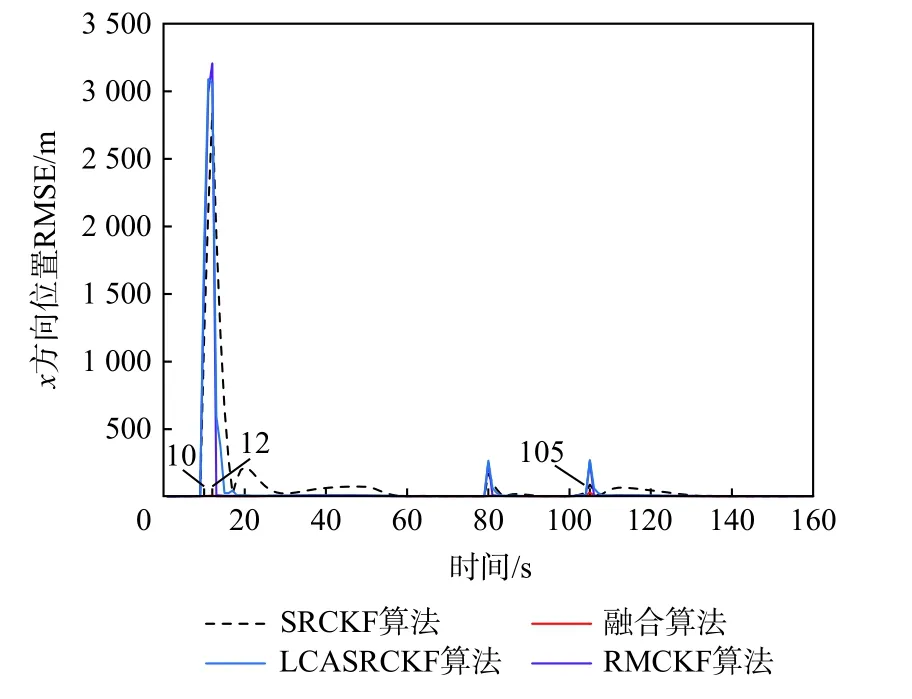
图5 x 方向位置均方根误差（场景2）Fig. 5 RMSE of position in y axis (scenario 2)

图6 y 方向位置均方根误差（场景2）Fig. 6 RMSE of position in y axis (scenario 2)

图7 x 方向位置RMSE 细节（场景2）Fig. 7 Details of RMSE of position in x axis (scenario 2)

图8 y 方向位置RMSE 细节（场景2）Fig. 8 Details of RMSE of position in y axis (scenario 2)

从图5 和图6 可以看到，在异常量测值引入的时刻，SRCKF、RMCKF 和LCASRCKF 这3 种算法的RMSE 曲线都出现很大的跳变，而RMCKF 算法能以快速的收敛速度迅速降低误差，LCASRCKF 算法收敛速度稍慢但也优于SRCKF 算法。值得注意的是，在异常量测值和模型误差同时发生时，LCASRCKF 和RMCKF 算法甚至出现了比SRCKF 算法更高的峰值，这也符合之前的分析：此时新息的偏差主要来自于异常量测值，LCASRCKF 算法在此时修正状态预测值显然难以克服其不良影响甚至使误差进一步增大；而对于RMCKF 算法而言，此时基于较大新息得到的渐消因子会对改进的量测误差协方差矩阵的鲁棒作用产生“抵消”，这种仿真现象也出现在了文献[30]中。

相比之下，本文所提融合算法在误差存在时有着理想的收敛速度，同时保持了较高的滤波精度和稳定性。融合架构中的融合输出系数S使得全局输出可以平衡并充分利用先验预测值和后验量测值在状态估计过程中所提供的信息，因此融合算法的RMSE 曲线始终保持相对平稳，没有出现其他算法那样的跳变。结合表2 可以看到，融合算法在滤波精度上的优势明显。

从图7 和图8 可以进一步看到本文融合算法对10 ～12 s 之间连续性的量测缺失也能保持鲁棒性；在80 s时状态突变和异常量测值的同时发生对融合算法的精度影响不大；但是在105 s 模型不匹配和异常量测值的同时发生使得融合算法产生了一个稍高的峰值。