基于最小化新息协方差的修正SRCKF 算法

杨永建，甘轶，李春辉，*，邓有为，肖冰松，彭芳

(1. 西北工业大学 电子信息学院，西安 710072； 2. 空军工程大学 航空工程学院，西安 710038)

容积卡尔曼滤波[1-2]（cubature Kalman filter，CKF）基于三阶球面径向原则逼近最优框架中的状态后验分布[3]，是一种新兴的非线性状态估计方法，在目标跟踪、信号处理和导航等领域[3]广泛应用。和扩展卡尔曼滤波[4]（extended Kalman filter，EKF）相比，CKF 不需要计算雅可比矩阵；和无迹卡尔曼滤波[5]（unscented Kalman filter，UKF）相比，CKF 在强非线性和高阶时的状态估计性能更加稳定。理论上已经证明，CKF 能够至少以二阶泰勒精度逼近各种非线性系统的后验协方差和均值[6]，具有简单、精度高、收敛性好等优点[7]。平方根CKF（square-root CKF，SRCKF）是CKF 的平方根版本[8]，进一步提高了算法的数值稳定性和滤波精度，同时减小了运算量。

由于实际系统的先验统计特性无法精确得到，且跟踪过程存在目标机动、状态突变、模型不匹配等问题，模型误差不可避免且会导致平方根容积卡尔曼滤波（square-root cubature Kalman filter, SRCKF）的滤波性能严重下降。

为了克服模型误差的影响，获得良好的目标跟踪性能，主要有两类方法：①提高目标建模的准确性或利用多模型提高模型的自适应性，如改进的当前统计（current statistical，CS）模型[9-10]和交互式多模型（interacting multiple model，IMM）[11]与SRCKF结合，有效改善了滤波器性能；②改进滤波算法构成自适应滤波器，如Sage 自适应滤波器[12-13]，基于渐消记忆滤波理论的强跟踪滤波器[14]（strong tracking filter，STF）。其中，STF 通过引入渐消因子实时调整增益矩阵，迫使残差序列保持正交，以此提高克服模型误差的性能[15-20]，在目标跟踪系统中被广泛使用。尽管STF 性能良好，但STF 是一种次优算法，而且存在渐消因子插入位置随意[21]的问题。

文献[22]中提出了一种基于修正卡尔曼滤波（amended Kalman filter,AKF）算法，可以克服目标状态突变和目标运动建模不准确的不良影响，在此基础上文献[23]基于概率论进一步优化了判定准则。但是文献[22-23]所提算法仅修正了状态值而未修正相应的协方差矩阵，会造成误差；且修正门限及修正参数的设置是基于经验的，也会对滤波精度和滤波稳定性造成影响。因此，文献[24]提出基于最小新息协方差的修正卡尔曼滤波算法，新的修正算法理论推导完善，避免了修正门限的设置，能够较好地解决由于模型误差而引起的滤波精度下降甚至发散的问题。文献[25]将修正算法应用到了数据缺失时的目标跟踪系统中，通过有效利用后期测量数据，提高了数据缺失时目标跟踪的精度和稳定性。文献[22-25]中修正算法的主要思想是利用后期的测量数据，增加对测量值的信任度，以达到对模型误差进行补偿的目的。

为了进一步提高修正思想的应用范围和性能，本文基于最小化新息协方差原则推导了相应的修正系数，并将其应用到SRCKF 算法中，提出了基于最小化新息协方差的修正SRCKF（amended SRCKF,ASRCKF）算法。仿真结果验证了所提算法的有效性，同时与SRCKF 和STF-SRCKF 算法相比，ASRCKF算法有着更高的位置、速度和加速度跟踪滤波精度。

1 目标运动建模与SRCKF 算法

目标运动建模考虑如下离散状态方程和量测方程：

2 修正思想与ASRCKF 算法

2.1 修正卡尔曼滤波

修正思想的核心源自式（16）。由式（16）可以看出，影响系统k+1 时刻状态估计的因素有2 个，①状态预测值；②来自新息或量测值的反馈修正。自适应滤波一般是对第2 个因素的增益进行修正，如STF 就是通过膨胀预测误差协方差来自适应地增大增益，从而增大量测值在滤波中的贡献以避免发散。不同的是，修正卡尔曼滤波着眼于第1 个因素即状态预测值，通过对状态预测值进行合理的补偿和修正，进而消除模型误差造成的偏差，达到降低预测误差和估计误差的目的。

在对量测值信任的基础上，k+1 时刻的新息rk+1发 生突变说明k+1 时刻状态预测值xˆk+1|k与真实值偏差较大，而这一偏差又源于k时刻目标机动或状态突变造成的状态估计值xˆk|k的不准确。因此，通过对k时刻状态估计值进行修正，并用修正后的状态估计值重新计算k+1 时刻的预测值，就可以减小预测误差进而减小估计误差。同时新息反映了预测值与真实值偏差的趋势和程度，所以对k时刻状态估计值的修正是基于新息的。

文献[22-24]将修正思想应用在卡尔曼滤波中，并对判定准则和修正准则不断改进。最初的判定准则和修正准则是基于经验的[22]，之后文献[23]基于概率论优化了判定准则。文献[24]基于最小新息协方差原则推导出修正系数的向量表达式，不仅避免了判定准则的设置，且修正系数也是基于理论推导得到的，减小了基于经验设置参数的影响。

2.2 修正系数推导

本文基于最小新息协方差准则来推导修正系数的向量形式。

对k时刻估计值按式（18）进行修正：

2.3 ASRCKF 算法实现

总结得到ASRCKF 算法的流程如图1所示，具体的实现步骤如下：

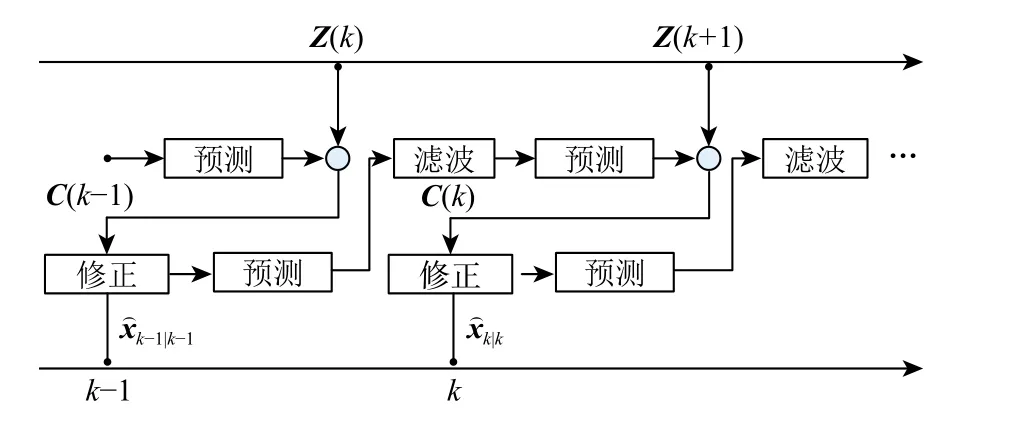
图1 算法流程Fig. 1 Flow chart of the algorithm

步骤 1 通过式（2）～式（17）完成时间更新及量测更新，得到SRCKF 的滤波参数。

步骤 2 用式（25）计算修正系数Ck，并通过式（18）和式（19）修正状态估计值和估计误差协方差矩阵。

步骤 3 用修正后的状态估计值和估计误差协方差矩阵重新按式（2）～式（17）完成滤波。

步骤 4 重复步骤1～3。

ASRCKF 算法利用了k时刻之后的量测值，类似于平滑算法但和平滑算法的本质不同。

为了验证ASRCKF 算法的有效性，将其与标准SRCKF 算法、STF-SRCKF[21]算法进行对比。仿真中目标做匀加速运动，状态转移矩阵和测量矩阵分别为

3 仿真与分析

目标初始状态为x0=[10 m，60 m/s，0 m/s2]T，系统初始协方差P0=diag(100,10,1)；系统过程噪声协方差矩阵中q=2，q为连续时间白噪声的功率密度，反映了模型误差的程度；量测噪声协方差R=100 m2；STF-SRCKF 算法中的遗忘因子取0.96。

仿真进行200 次蒙特卡罗实验，同时用目标位置，速度和加速度的均方根误差（root mean square error, RMS E）作为评价指标：

仿真场景1 主要考虑状态突变造成的模型误差。目标初始运动状态为x0=[0 m，50 m/s，0 m/s2]T，前30 s 目标保持状态不变，在31 s 时加速度突变为20 m/s2，在81 s 时加速度突变为-20 m/s2。每次蒙特卡罗仿真的初始估计状态为xˆ0=[0 m，50 m/s，0 m/s2]T，初始估计误差较小。

图2～图4 分别为目标位置、速度和加速度的均方根误差对比，表1 为3 种算法误差均值对比。

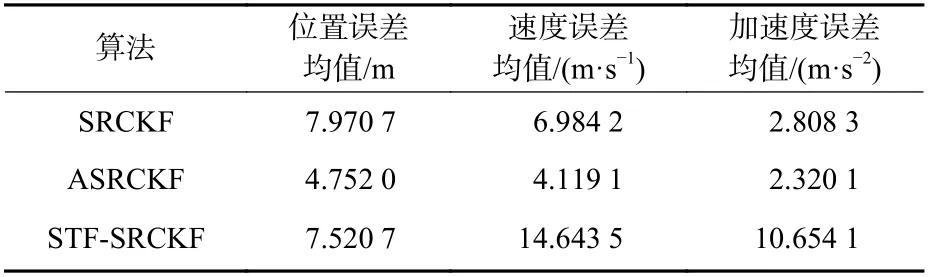
表1 场景1 误差均值对比Table 1 Comparison of mean error for each algorithm in case 1

对目标位置的跟踪是关键，从图2 可以看出，SRCKF 算法在滤波正常时比STF-SRCKF 的跟踪精度更高，但是在引入加速度突变的31 s 和81 s，其RMSE 曲线发生跳变，产生较大误差。而ASRCKF和STF-SRCKF 能够克服状态突变的不良影响，始终保持较为平稳的跟踪精度；同时可以明显看到ASRCKF 有着比STF-SRCKF 及SRCKF 更好的滤波精度。从图3 和图4 中速度和加速度跟踪误差可以看到，在状态突变发生时，ASRCKF 算法有着更高的精度及更快的收敛速度。

图2 场景1 位置均方根误差Fig. 2 RMSE of position in case 1

图3 场景1 速度均方根误差Fig. 3 RMSE of velocity in case 1

图4 场景1 加速度均方根误差Fig. 4 RMSE of acceleration in case 1

结合表1 可以看到，尽管STF-SRCKF 有着较好的滤波稳定性，但却是次优算法，在速度、加速度的跟踪精度上还要低于SRCKF。相比之下，ASRCKF在位置、速度、加速度跟踪精度上都要明显更优。

仿真场景2 在场景1 的基础上，一方面引入模型不匹配造成的模型误差，即在50～55 s 期间3 种算法均使用匀速直线运动的状态转移矩阵来代替CA 模型中的 Φk；另一方面设定仿真初始估计状态为xˆ0=[60 m，0 m/s，20 m/s2]T，从而引入较大的初始估计误差；其余设置和场景1 相同。

图5～图7 分别为场景2 中目标位置、速度和加速度的均方根误差对比，表2 为3 种算法在场景2中的误差均值对比。

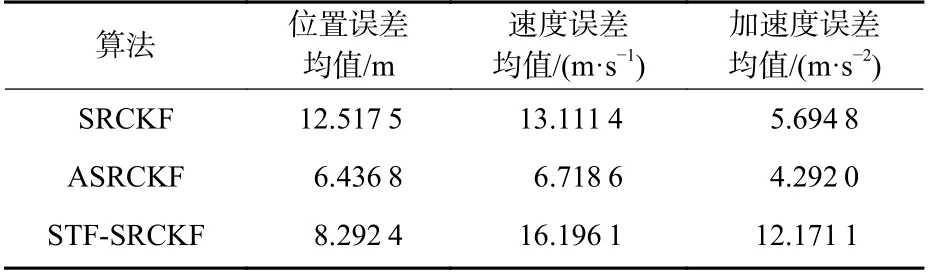
表2 场景2 误差均值对比Table 2 Comparison of mean error for each algorithm in case 2

仍然从位置跟踪上进行分析，如图5 所示，在较大初始误差引入下，ASRCKF 和STF-SRCKF 有着比SRCKF 更好的误差收敛速度；在31 s 和81 s引入的加速度突变对3 种算法的影响和场景1 仿真结果一致；在模型不匹配引入的50～55 s，STFSRCKF 的稳定性最好，其他2 种算法都出现了RMSE曲线的跳变，但是ASRCKF 受到的影响更小。如图6 和图7 所示，在状态突变和模型误差发生时，STF-SRCKF 无法保持位置跟踪时的良好稳定性和精度；相比之下ASRCKF 算法保持着更低的滤波误差及更快的收敛速度。

图5 场景2 位置均方根误差Fig. 5 RMSE of position in case 2

图6 场景2 速度均方根误差Fig. 6 RMSE of velocity in case 2

图7 场景2 加速度均方根误差Fig. 7 RMSE of acceleration in case 2

结合表2 可知，STF-SRCKF 在位置跟踪上的精度和稳定性比较好，但是在速度、加速度跟踪上却不理想；相比之下，ASRCKF 在位置速度、加速度跟踪精度上都要明显更优。

4 结 论

为了克服模型误差带来的不良影响，同时，进一步提高修正思想的应用范围，本文基于最小化新息协方差原则推导了相应的修正系数，并将其与SRCKF 算法结合，提出了ASRCKF 算法。仿真结果表明：

1) 目标状态突变存在时，ASRCKF 有着更好的滤波性能，收敛速度更快；从位置、速度和加速度误差均值上看，ASRCKF 都是最低的。

2) 在引入较大初始误差和模型不匹配后，ASRCKF 依旧保持着高滤波精度和快速收敛速度，位置、速度和加速度误差是3 种算法中最低的。

3) ASRCKF 算法的有效性和优良跟踪性能得到验证，有效地提高了SRCKF 算法的场景适应能力。