轻量化二维指向调整机构设计
2023-02-09曲华杰张立华曲建俊
曲华杰,黎 明,张立华,曲建俊
(1.哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001;2.航天东方红卫星有限公司,北京 100086)
1 引言
目前各国正在研制新一代单体大孔径角锥激光反射器,以减小测距误差[1]。但是,当进行地月测距时,如果地面发射的激光入射角发生偏斜,就会造成激光回射功率的减小并产生附加光程差,因此研制新一代激光反射器用地月二维指向调整机构十分必要[2]。中大型空间指向调整机构国内外已有一些研究[3−4]。随着微纳卫星发展,对小型轻量化指向机构需求日益增加,各国开始选用新型电机来研究机构的轻量化和小型化[5],在满足调整功能要求的前提下实现机构的高精度和轻量化设计成为重点研究方向[6]。拓扑优化和有限元强度法是常用的机构轻量化设计方法[7−8],它们主要针对机构本身的质量和尺寸,以及支撑方式等进行优化[9],很少涉及机构的驱动源。为了设计一种直接驱动高精度轻量化指向机构,超声电机是首选驱动源。但是,如何利用小型的超声电机驱动较大质量的反射器是值得研究的。
这里以设计新一代激光反射器二维指向调整机构为研究目标,研究轻量化二维指向调整机构质心平衡设计法及评价指标,推导2级调整机构负载力矩表达式,确定质心位置及变化域,研制原理性样机,旨在实现二维指向调整机构的轻量化设计。
2 二维指向调整机构的质心平衡设计
2.1 机构轻量化设计方法
提出以机构的载重比Q作为机构轻量化的衡量,定义为式(1),载重比为机构驱动负载的质量和机构自身的质量之比:

式中:mf—负载质量;mj—机构质量。
Q的值越大代表机构的越轻盈,经计算很多空间指向调整机构的Q值均远远小于1,以中国科学院某设计的星载太阳指向器为例,其载重比Q值为0.24。在这里不妨以Q值能否大于1作为机构的轻量化分界标准。
指向调整机构主要包括驱动源和机构,欲实现轻量化设计,就要尽可能减小每个组成部件的质量,因此机构驱动源的选择和构型方案的设计就是关键技术。这里提出驱动源(电机)的选择原则为:在满足驱动性能要求的基础上,选择质量最轻的驱动电机为机构动力源。在机构构型设计中,提出二维指向机构质心平衡设计法,通过负载自身质量的平衡,减小电机负载力矩的大小,从而选择小尺寸型号电机以及优化匹配部件尺寸,实现整机的小型化和轻量化。
2.2 轻量化驱动源的确定
选择两类驱动电机,其性能比较,如表1所示。从表1可见,在指向机构要求的性能指标上,超声电机(USM)具有明显的优势,因此,选择超声电机作为机构驱动源。
超声电机除具有表1优点外,还具有电磁兼容性好、响应快、适合太空环境等特点,可以很好地匹配机构对驱动电机的要求,其断电自锁的性能避免增加锁紧机构,简化了整机复杂度,减轻了机构的质量,如表1所示。

表1 两种驱动电机的性能比较Tab.1 Performance of Two Kinds of Drive Motors
以质心平衡为设计理论,基于超声电机为驱动源设计了机构方案,选择俯仰−方位型调整方式,用L板连接负载和电机,编码器为角度检测装置实现二维指向调整。设支架底平面与水平面夹角为β,考虑支架不水平放置的一般情况,二维指向调整机构模型,如图1所示。
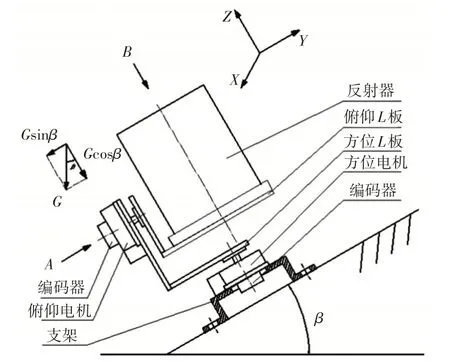
图1 二维指向调整机构模型Fig.1 Model of Two−Dimensional Pointing Adjustment Mechanism
该方案组成部件包括:俯仰超声电机、方位超声电机、俯仰L板、方位L板和两个编码器以及支架等。采用俯仰超声电机和方位超声电机分别对指向调整机构的俯仰角和方位角进行角度调整,充分利用超声电机性能特点实现机构所有功能。
该方案的特点是整机组成元件少,无需复杂机械装配。在新一代激光反射器的负载条件下,根据质心平衡设计方法,通过设计L板的放置位置,使各电机所驱动的负载质心位置靠近电机回转轴,减小了负载质心距离电机回转轴的距离,从而大大减小电机负载力矩的大小。
2.3 方位和俯仰电机驱动力矩
电机驱动力矩是选型的重要依据,必须克服负载力矩的最大值,负载力矩受电机俯仰角、方位角、倾斜角和负载质心距回转轴的距离等因素影响。
根据机构调整角范围,设俯仰电机俯仰角为θ1∈(−90,90),方位电机转角为θ2∈(0,360),安装支架倾斜角为β∈(−90,90),指向机构在月面安装时可能因月貌环境的凹凸不平,使安装支架的平面发生倾斜,为了保证机构在所有情况都能可靠运行,需要对所有工况进行分析,分别设机构进行俯仰角和方位角调整时电机的负载力矩为Mp和Ma,负载力距回转轴距离为L。由图1中B方向可得重力在俯仰电机旋转方向分力为G1,在方位电机旋转方向分力为G2,分别从A、B所示方向观察沿电机轴向电机转动受力,如图2所示。
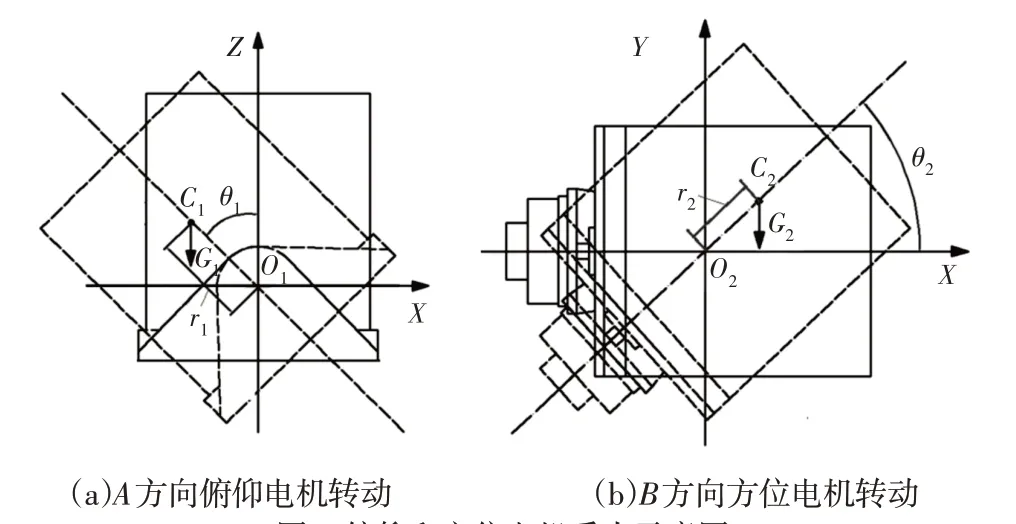
图2 俯仰和方位电机受力示意图Fig.2 Force Diagram of Pitch and Azimuth Motors
如图2(a),在XO1Z坐标系,其中O1为与俯仰电机回转轴重合的坐标系原点,设C1为俯仰电机所驱动负载质心位置,G1=G·cosβ,为俯仰电机的负载力,r1为质心与电机回转轴间的距离,θ1为俯仰电机转动的俯仰角,m1为俯仰电机所驱动负载质量。则可得考虑安装支架倾斜的情况下俯仰电机的负载力矩为:
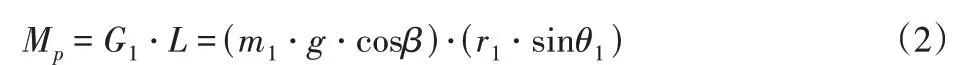
从式(2)可以看出,负载力矩大小与俯仰角度和支架倾斜角度有关,根据各角度变化范围可得,当机构支架倾斜角β为0°,俯仰角θ1为90°时俯仰电机负载力矩最大。
如图2(b),在XO2Y坐标系,其中O2为与方位电机回转轴重合的坐标系原点,设C2为方位电机所驱动负载质心位置,G2=G·sinβ,为方位电机的负载力,r2为负载质心与电机回转轴间的距离,θ2为方位电机转动的方位角,m2为方位电机所驱动负载质量。则可得考虑安装支架倾斜的情况下方位电机的负载力矩为:

从式(3)可见,方位电机负载力矩随支架倾斜角和方位角而改变,注意到,r2也是随俯仰角变化的,因此方位电机负载力矩一共受3个因素的影响。
经分析当倾斜角β为90°,方位角θ2为0°,俯仰角θ1为90°时出现方位电机负载力矩的最大值,选用的方位电机的驱动能力必须大于该力矩值。
由式(2)、式(3)可以得出,无论是俯仰电机还是方位电机的负载力矩,都与负载质心到回转轴距离r密切相关,减小r可以从根本上减小负载力矩的大小,进而选择小尺寸型号超声电机和部件尺寸,实现机构的轻量化设计。
3 质心位置设计
为了准确控制电机负载力矩,需要确定机构的质心。对不规则物体,需要对机构合理简化,利用质心位置计算公式确定质心的位置[10]。根据指向调整机构使用环境和技术要求,选取高性能铝合金钢7075等为机构材料,分别推导出方位和俯仰电机负载质心位置。
3.1 俯仰电机负载质心位置
俯仰电机负载主要包括俯仰L板和反射器,需要确定俯仰L板和反射器的质心位置。根据机构特点,建立坐标系,如图3所示。分别在俯仰L板弯折面上建立基准坐标系O1和反射器底面中心建立坐标系O2,坐标系O2相对O1平移了(80+t,0,b)。其中t和b值含义,如图4所示。
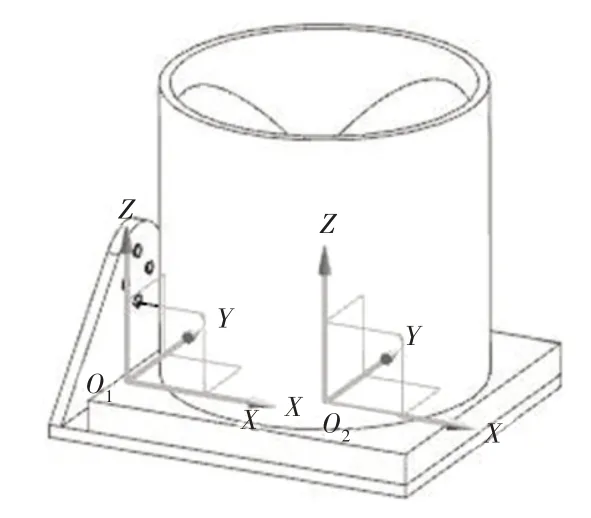
图3 俯仰电机驱动部件基准坐标系O1和O2Fig.3 Reference Coordinates of Driving Components of Pitch Motor
把俯仰L板和反射器组成的整体分为m1、m2和m3三个质量部分,俯仰L板被分为m1和m2,反射器看成整体质量单元m3,如图4所示。
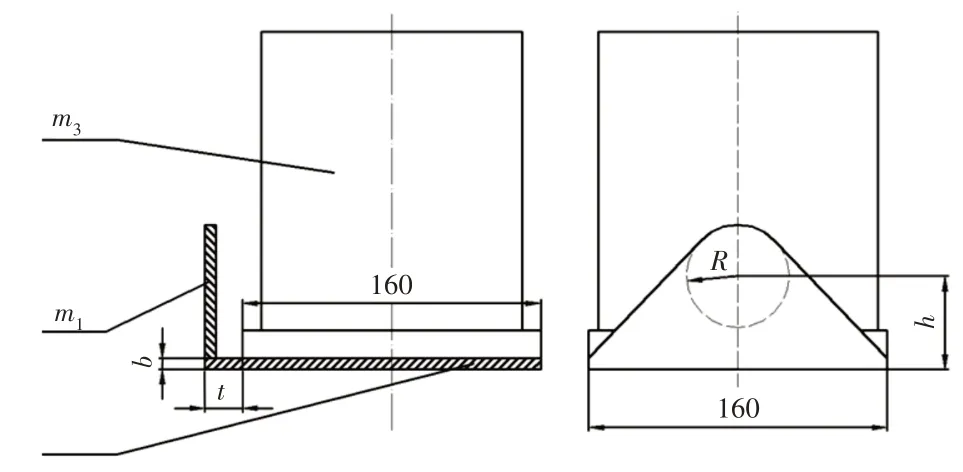
图4 俯仰电机所驱动部件Fig.4 Components Driven by Pitch Motor
利用转换矩阵建立俯仰L板和反射器在基准坐标系下的质心位置求解式,求解整体质心位置Pc的坐标,如式(4)~式(6)所示。

利用质心计算式(4)~式(6),可求出俯仰电机回转轴放置位置。根据设计经验结合电机连接尺寸,选取俯仰L板板厚b为6mm,反射器位置距离t=20mm,圆心高度h=52mm,半径为R=27.5mm,z1为41.334mm,m1质量块质量为111.5g,质量块m2质量为486g,反射器质量m3为5.5kg,质心高度Z3为51mm。带入式(4)~式(6),可得三个质量块整体在基准坐标系O1下的质心位置为(97.43mm,0,52.43mm),则可设计俯仰电机回转轴轴心位置高度为52mm。
3.2 方位电机负载质心位置
方位电机转动时将驱动调整机构大部分部件运动,主要包括反射器、俯仰L板、俯仰电机、编码器、方位L板等部件。同理,可按俯仰电机负载质心确定法计算出各部件在基准坐标系下的质心位置,再求得整体质心位置。
但因方位电机转动时,俯仰电机也会运动,导致方位电机所驱动部分部件的质心位置发生改变,则需在不同极限位置处求得所有部件的质心域,确保选择的方位电机可以满足使用要求。
首先,将方位电机负载进行拆分,分别求得在不同坐标系下的质心位置。
然后,利用交换矩阵将质心位置换算到同一坐标系下,最后,利用质心位置公式求解质心位置。根据方位电机结构特点,建立坐标系O3和O4,如图5所示。

图5 方位电机驱动部件基准坐标系O3和O4Fig.5 Reference Coordinates of Azimuth Motor Drive Components
可以推导出方位电机所驱动负载质心位置在坐标系O3下的质心坐标,如式(7)~式(9)所示。

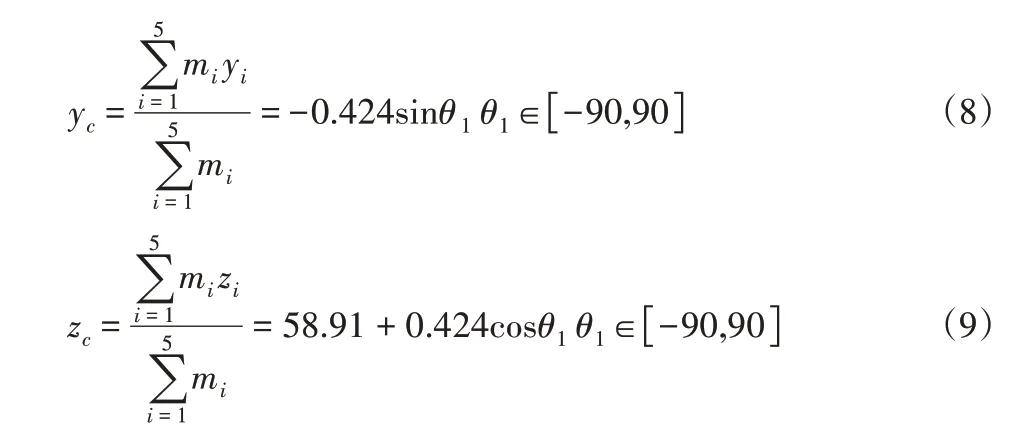
式中:θ1—俯仰电机转动的俯仰角;mi—代表拆分的各部分质量;xi、yi、zi—分别代表拆分的各部分质心位置坐标。利用式(7)~式(9),可以在O3坐标系下设计出方位电机回转轴位置为(103,0,58)。
已知俯仰电机的角度转动范围为(−90~90)°,方位电机的角度调整范围为(0~360)°,以及机构安装支架倾斜角度最大变化范围为(−90~90)°。利用质心坐标公式求得其质心相对底座中心的变化为一曲面,可得在安装支架水平时机构整体质心位置所在曲面,如图6所示。
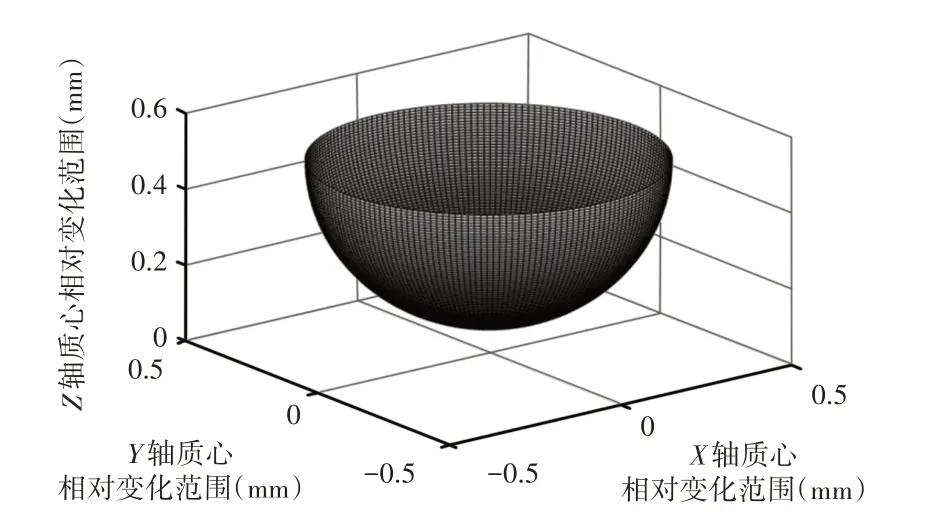
图6 安装支架水平时机构质心位置曲面Fig.6 Surface of Centroid Position of Mechanism on Horizontal State of Mounting Bracket
可以得出,俯仰电机所驱动负载质心位置是固定的,容易选择电机。但是,方位电机所驱动负载质心位置会发生变化,这是难以通过减小质心与方位电机回转轴距离来消除的,因此所选用的方位电机应保证在整个质心变化域范围内都可以驱动和锁紧机构。经过质心位置分析,可以设计出电机回转轴位置,考虑减小负载力矩,根据负载条件要求,经计算得出,选用60型超声电机可以可靠驱动所设计的机构。
4 机构质心平衡实验
为了验证设计原理的正确性,制作了指向调整机构原理样机,设计了模拟质心调节器,该调节器主要由质心调节螺母,螺杆和螺杆座组成,其质量设计为反射器质量的极大值,并且外形尺寸和反射器近似,采用与反射器相同的安装方法。其中指向机构部件总质量为1.526kg,满足了机构的质量和外形尺寸的技术指标要求,模拟反射器(质心调节器)部分总质量为5.412kg。通过质心调节螺母可以调节负载质心位置,经计算,每旋转一圈质心位置改变1.234mm,通过改变质心位置可以检验样机的驱动、自锁性能,验证设计合理性。
样机所用超声电机锁紧力矩为1.5N·m,装配完成后调整螺母至设计的质心位置处,当俯仰角为90°时机构处于锁紧力矩最大状态,若此位置可以锁紧,则可保障机构任意位置可靠锁紧,结果表明,机构可在任意位置锁紧。机构能否驱动负载,实现大范围角度调整也是关键的性能,在电机安装前,测量了电机最大驱动力矩,电机最大驱动力矩随频率变化,如图7所示。可见,60型超声电机的最大驱动力矩可达1.05Nm,随频率变化呈现逐渐减小趋势。

图7 电机空载驱动力矩随频率变化Fig.7 Variation of No−Load Driving Torque of Motor with Frequency
为了验证质心设计原理,利用质心调节器改变负载质心到回转轴的距离,可以找到不同驱动信号下可靠驱动负载的最大质心偏移距离。因为机构的负载力矩随俯仰角变化,当俯仰角为90°时产生的负载力矩最大,需在此位置检验样机能否驱动负载,确定最大质心变化范围。根据安装前测量的超声电机驱动力矩可以计算出机构可驱动质心范围的理论值。俯仰电机的负载为质心调节器和俯仰L板,其质量为F=6.012kg,取重力加速度g=9.8m/s2,则不同驱动力矩M下的可驱动质心范围理论值Pt可按照式(10)计算。

这里用质心调节螺母旋进深度h来表示质心位置变化情况,负载质心与回转轴重合时理论设计值h为51.3mm,h的值与51.3mm相差越大,质心变化也越大,需要的驱动力矩也就越大。h值每变化一个螺距(4mm),质心改变1.234mm,通过测量h值,可以用式(11)计算质心位置实际值Pe。

质心位置的试验值和理论计算值比较,如图8所示。
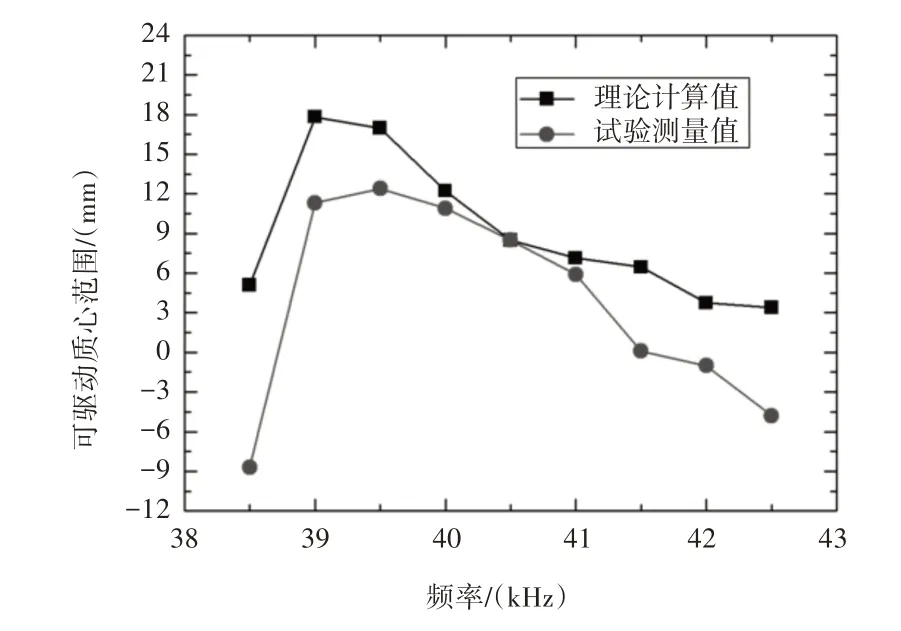
图8 超声电机可驱动质心范围随频率变化Fig.8 Variation of Driving Center Range of Motor with Frequency
从图8 的试验结果可以看出,在选定的驱动信号频率范围内,当机构质心从−8.7mm到+12.4mm变化时,所选择的超声电机可以可靠驱动负载,电机可驱动质心范围随驱动信号频率变化而变化,其变化趋势与试验测量的电机驱动力矩变化相同,如图7所示。驱动力矩越大,质心变化范围就越大。同时可以看出,当电机驱动信号频率改变时,试验测量出的可驱动质心范围和理论计算值的变化趋势相同,说明电机驱动力矩减小时,可驱动质心范围也变小,反过来,如果减小质心位置到回转轴距离,就可以有效减小负载力矩大小,就可以选择驱动力矩小,质量轻的超声电机,从而验证了质心平衡设计原理的正确性。
但实际测量得到的可驱动负载质心范围和理论计算值存在误差,产生误差主要有以下原因:(1)用理论公式计算负载质心位置时进行了部分简化,比如对质量和负载外形进行简化处理;(2)本设计为电机直接驱动负载,当加上负载(模拟质心调节器)后,负载使电机轴产生了微小变形,这一方面使电机定转子间接触状态发生改变,导致电机输出力矩发生改变,另一方面造成了质心位置的偏差。目前所用超声电机为购置产品,今后需要开展提高转子轴的刚度研究。
5 结论
提出了基于质心平衡的二维指向机构轻量化设计方法,定义的载重比可以用来评价机构的轻量化程度。设计出一款超声电机驱动的二维指向调整机构的轻量化构型方案,得到了机构质心位置变化域,制作出原理样机,完成了样机性能测试实验。结果表明,机构整机质量为1.526kg,按反射器5.4kg计算,载重比可达3.5,可实现任意位置自锁和大范围角度调整,验证了这里提出的质心平衡设计原理的有效性。
