基于双自适应无迹卡尔曼滤波算法的锂电SOC/SOH联合估计
2023-02-09王若琦王晓佳郭凯丽
王若琦,王晓佳,杨 淇,郭凯丽
(太原理工大学机械与运载工程学院,山西太原 030024)
1 引言
为实现节能降耗,降低污染,发展节能环保、不依赖化石燃料的电动汽车取代传统燃油车,已成为当今世界汽车行业的重点发展方向。锂离子动力电池准确可靠的状态估计是电动汽车安全运行的基础[1],其主要包括荷电状态(SOC)和健康状态(SOH)。SOC直接反映了电池剩余电量的大小,其准确估计直接关系到电动汽车的能量动力分配。
SOH 是电池老化程度的一项重要指标,通常表现为电池的能量密度、功率密度、容量的衰减和内部电阻增大[2],电池状态的准确估计可以使电池得到充分合理的利用,避免电池突发故障造成的危害,对于电动汽车的安全运行具有重要意义[3]。
目前国内应用最多的电池SOC 测量方法是安时积分法,它计算简单,但受初始SOC误差的影响较大,且会随时间增长出现较大的累计误差[4]。另外,电池SOC测量方法还有开路电压法、卡尔曼滤波法、神经网络法。开路电压法容易实现但需要通过静置校准OCV值,不利于实际运用[5]。
神经网络法通过训练大量的样本数据进行估算,准确性受训练的方法及训练量大小影响较大,计算量太大。卡尔曼滤波法使用递推迭代的方法对SOC 进行估算[6]。最常用的为扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF):EKF估算过程中容易由于线性化过程中方差矩阵的非正定性导致估计值不收敛;UKF利用无迹变换处理均值和协方差,可以有效提高对非线性分布统计量的估算精度,但是系统噪声的预定变量设置不当通常会导致系统误差和发散[6]。
国内外常用的SOH估计方法有定义法、电化学阻抗谱分析法、容量衰减法等。定义法是以电池的定义为基础,应用电池内部特征量变化前后的比值关系来对电池的进行估计,此方法需要反复充放电实验,在实际中很难实现[7]。电化学阻抗谱分析法对仪器的精度要求高,投入较大,性价比不高。容量衰减法是通过数学建模实验得出容量衰减的规律,属于定性的方法分析SOH[8]。
针对目前电池状态估计精度和实用性不理想的问题,常以表征电池老化的主要参数容量和内阻来定义SOH。相对来说,电池容量与SOH之间的关系更为直接且容易采集[4],所以这里选择容量作为估计SOH的状态变量,其定义为在一定条件下锂离子动力电池能够充入或放出的最大容量占其额定容量的百分比[9],如下式所示:

式中:Qnow—电池现有的最大的容量;Qstart—电池的额定容量。
基于以上分析,目前锂离子动力电池状态参数的研究中,多是将SOC与SOH分开研究,对两者在电池状态参数估算过程中的相互影响考虑较少[10]。
为此,这里提出自适应无迹卡尔曼滤波算法(AUKF),并在其基础上,采用双自适应无迹卡尔曼滤波(DAUKF)对SOC 和SOH联合估算,通过两个滤波器的结合,实时更新计算模型中的参数。最后通过实验验证了算法的可行性及估算精度。
2 电池状态空间模型
目前锂离子动力电池模型有很多,常见的电池电路模型有经典的Rint、RC、Thevenin 和PNGV 模型等。Thevenin 电池模型很好的模拟了电池的极化反应,而且结构简单,计算量较小且容易实现[11]。所以选用Thevenin电池模型,如图1所示。

图1 Thevenin电池模型Fig.1 Thevenin Battery Model
图中:UOCV()soc,t—电压源,表征SOC与开路电压的非线性关系;U—动力电池实际工作电压;I—电池工作电流;RO—电池的欧姆内阻;RP、CP—锂离子动力电池的电化学极化电阻和电容,用于模拟电池动态特性中表现出的短时间常数。以电池的荷电状态SOC、电容上的电压UP作为状态变量,记状态变量X=[]SOC,UP;以电流I作为输入量;以电池端电压UO为输出量。根据Thevenin等效电路模型,建立锂离子动力电池模型的离散化状态方程:
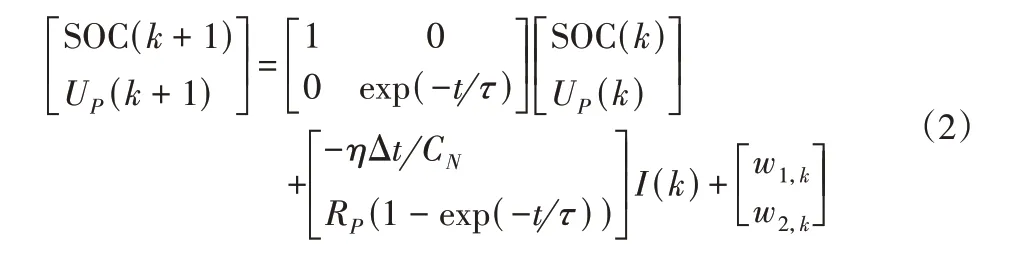
离散化输出方程为:

式中:t—采样时间;CN—电池容量;K—离散时间变量。
τ1=RPCP,系统噪声为wk=[w1,k w2,k]T,其协方差为Q;观测噪声为vt,其协方差为R。
3 电池模型参数离线辨识
本次实验以中航锂电的CA63CF锂离子动力电池为实验对象。由台式电脑、可编程充放电仪和对应的记录监控软件等组成实验平台,设计电池在常温下分别以大电流1C恒流充(放)360s,小电流0.01A恒流充(放)430s的循环脉冲充放电实验,通过可编程充放电仪根据需要设定不同的工况条件对电池进行充放电,最后根据监控软件实时采集和存储电池的工作数据。电池的开路电压OCV与荷电状态SOC之间为非线性的关系[12]。这里通过快速法[11]来确定电池OCV与SOC的关系曲线。快速法的原理是利用某一特定电流做充放电循环实验,SOC每间隔10%时静置一段时间,分别拟合充电过程中静置阶段的极小值点和放电过程中静置阶段的极大值点,这两条曲线的平均值即为OCV与SOC之间的关系曲线。
该锂电池最终拟合的OCV−SOC关系曲线,如图2所示。

图2 锂电池的OCV−SOC关系曲线Fig.2 OCV−SOC Relationship Curve of Lithium Battery
这里通过1C 的HPPC 实验对Thevenin 模型中的电容、电阻等参数进行辨识。步长为10%,电池脉冲放电电压曲线,如图3所示。放电结束时,由于欧姆内阻分压的突然消失造成电池的端电压从U1瞬间上升至U2,所以欧姆内阻可表示为:
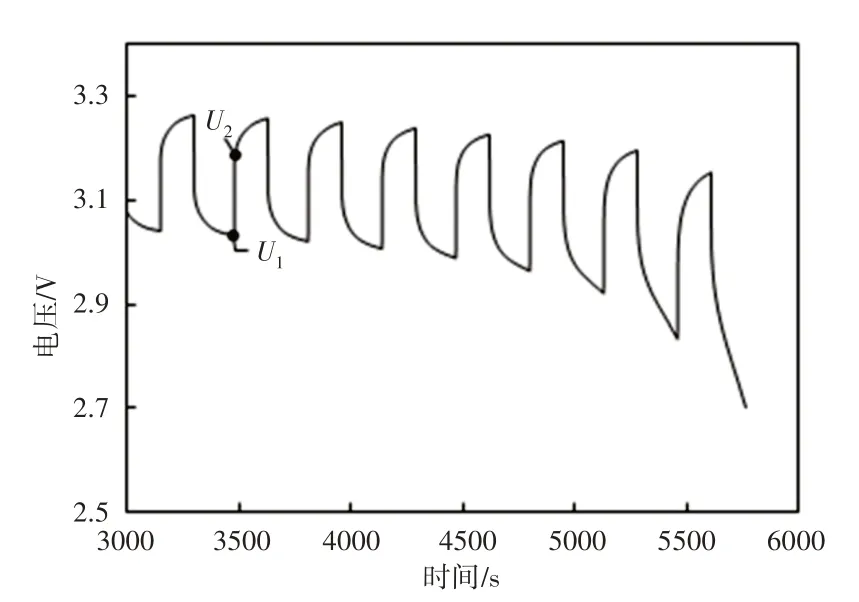
图3 电池脉冲放电电压曲线Fig.3 Pulse Current Discharge Voltage Change Diagram

RC回路在静置阶段变为零输入响应,有如下关系:

对式(5)进行指数拟合,通过使用MATLAB 中Curve Fitting工具箱,可求得k和k1的参数值。
根据拟合参数与极化电阻和极化电容之间的关系,可以得到:

根据以上公式,可以辨识得到电池的初始参数RO、RP、CP,如表1所示。

表1 Thevenin模型参数辨识结果Tab.1 Thevenin Model Parameter Identification Result
4 DAUKF算法联合估算SOC、SOH
4.1 UKF算法原理
无迹卡尔曼滤波算法(UKF)是通过UT变换,在状态变量附近选取采样点,对于给定的非线性系统,空间状态方程可以由下式描述:

式中:f—线性状态方程函数;h—非线性观测方程函数。用UKF算法估计状态变量具体过程如下所示:
(1)算法初始化:


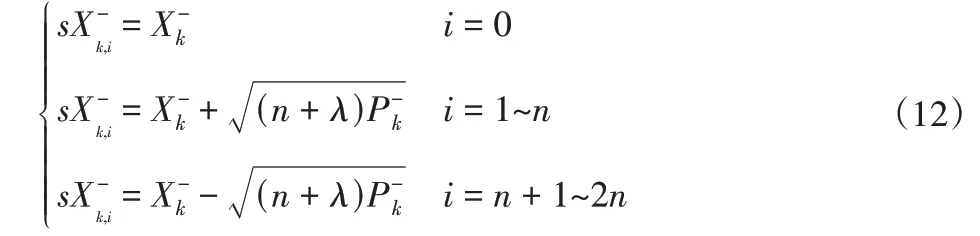

(6)求新的Sigma点集的观测预测值,利用加权求和求得系统预测的均值和协方差:

4.2 自适应无迹卡尔曼滤波算法(AUKF)
传统无迹卡尔曼滤波(UKF)算法在应用时,常常由于难以真实模拟实际噪声变化,而使得估算误差增大。因此这里提出自适应无迹卡尔曼滤波算法(AUKF):为了更真实的模拟实际噪声,实时更新计算观测变量和预测变量之间的误差,然后依据此误差值将观测噪声和系统噪声进行实时更新。误差值如式(25)所示,其中,ek—新息序列,Hk—新息序列协方差函数,M—开窗的大小。

更新后的系统和观测噪声协方差如下式所示:

4.3 DAUKF联合估算SOC与SOH
要实现DAUKF算法对SOC与SOH的联合估算,首先需要建立电池SOC及容量的状态空间方程[3]。SOC的状态方程式(2)、式(3)已经给出,容量的状态空间方程为:

式中:r(k)—均值为零、方差为r的高斯白噪声,用来模拟电池容量Q的衰减过程。v(k) —均值为0、方差为v的测量噪声。
根据两组状态空间方程,可得到DAUKF算法联合估算电池SOC与容量。具体流程,如图4所示。算法由两个卡尔曼滤波器组成;在每个采样时刻,算法会利用上一时刻容量Q的估计值根据式采用AUKF算法估算SOC;然后以SOC为已知量,再次运用AUKF算法估算Q;通过反复的循环迭代计算,实现对电池SOC与容量Q的实时联合估算。

图4 DAUKF算法流程图Fig.4 DAUKF Algorithm Flowchart
5 仿真结果与分析
为了充分验证该算法的可行性及精度、稳定性,在多次恒流充放电实验基础上,分别利用传统的UKF和这里提出的DAUKF通过MATLAB 进行仿真,将SOC及容量实时估计结果与实测电池SOC和容量曲线进行对比。仿真结果,如图5~图8所示。

图5 采用不同算法估计SOC的结果对比图Fig.5 Comparison of the Results of SOC Estimation Using Different Algorithms
从图5~图6可以看出,传统的UKF在估计SOC时误差较大,且会随时间推移出现误差的累积,而DAUKF算法可以非常精确地跟踪实验值的变化,估算最大误差在2%以内;从图7~图8可看出,采用DAUKF算法预测得到的容量曲线可以很好的模拟真实容量衰减曲线,估算容量误差小于0.07Ah,误差百分比在0.13%以内。说明这里提出的DAUKF 算法对锂离子动力电池SOC 和SOH进行联合估算是准确可行的。

图6 采用不同算法估计SOC的结果对比图Fig.6 Comparison of Errors in Estimating SOC Using Different Algorithms

图7 采用DAUKF算法估算容量结果对比图Fig.7 Comparison of Estimated Capacity Using DAUKF Algorithm
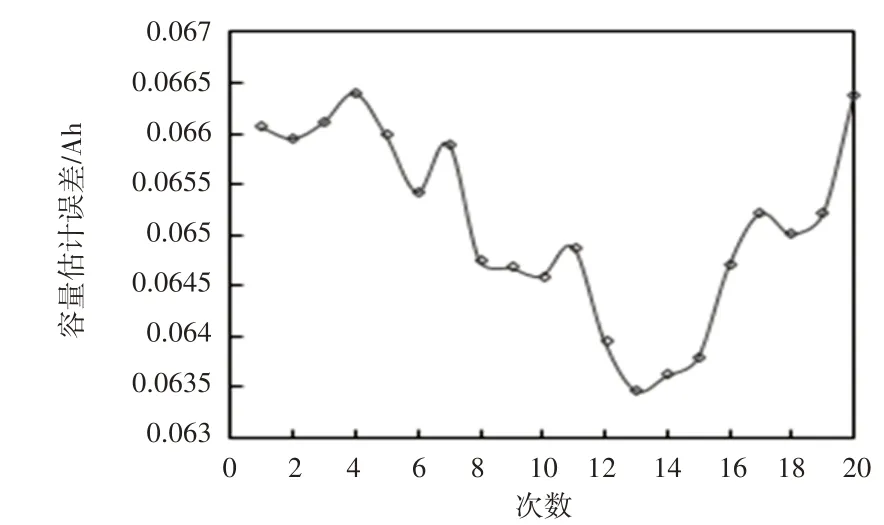
图8 采用DAUKF算法估计容量误差图Fig.8 Estimation of Capacity Error Using DAUKF Algorithm
6 结论
(1)针对传统无迹卡尔曼滤波(UKF)难以真实模拟实际噪声变化而使得估算误差增大的问题,这里提出一种自适应无迹卡尔曼滤波(AUKF)算法,通过自适应因子实时更新计算观测值和预测值之间的误差,模拟实际噪声,从而提高SOC估计精度。
(2)针对目前锂离子动力电池状态参数的研究中,较少考虑两个参数在估算过程中相互影响的问题,这里在AUKF的基础上提出双自适应无迹卡尔曼滤波算法(DAUKF),实时更新模型参数,实现SOC和SOH的联合估算。
实验验证了算法的可行性和有效性,DAUKF对SOC和SOH估算具有较强的稳定性和精度,对比传统的UKF 算法估计SOC精度和稳定性有了较大的提高,满足实际的应用要求。
