磁悬浮轴承非线性支承特性的研究
2023-02-09王念先王东雄
田 聪,王念先,王东雄,徐 波
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北武汉 430081;2.武汉科技大学湖北省机械传动与制造工程重点实验室,湖北武汉 430081;3.东风越野车有限公司,湖北武汉 430058)
1 引言
磁悬浮轴承是利用电磁铁产生可控支承力将转子无接触地稳定悬浮的一种新型轴承。与普通机械接触式轴承相比,磁悬浮轴承具有无摩擦、无磨损、长寿命、无需润滑以及刚度阻尼可调等优点,这使得运动部件能够高速度、高精度、低功耗、无噪声地运行[1−2]。
目前关于磁悬浮轴承支承特性的研究所采用的模型大多是在平衡位置对非线性动力学方程进行线性化。
文献[3]对线性磁悬浮轴承系统进行动态仿真,对磁悬浮轴承支承特性的影响因素进行了研究;文献[4]采用了磁悬浮轴承的线性模型对支承特性的主动可控性进行了研究。然而磁悬浮轴承系统具有典型的非线性特性,动态性能复杂,将磁悬浮轴承抽象成为一个线性系统,会使整个系统的稳定性分析存在偏差。另一方面,关于磁悬浮轴承支承特性的研究所采用的系统模型是忽略漏磁及磁饱和的非线性支承力模型,文献[5]采用非线性支承力模型(忽略磁饱和、漏磁等)结合PD控制,研究了磁悬浮轴承支承刚度与控制器参数之间的非线性关系。然而,当磁饱和发生时,软磁性材料的磁阻显著增加,同时漏磁也是不可忽视的,文献[6]针对边缘磁通、漏磁及磁饱和等主要因素建立了磁悬浮轴承的承载力模型,并验证了承载力模型的正确性;文献[7]对磁化非线性进行精确建模,考虑了磁饱和问题,以实现控制器的开发;文献[7]建立了一个三极磁悬浮轴承模型,其中饱和效应被建模为气隙的不平衡增加,以研究磁饱和的影响。
以上对磁悬浮轴承支承特性研究,所采用的是在平衡位置附近进行线性处理的线性支承力模型或者忽略漏磁及磁饱和的非线性支承力模型,在一定的情况下可以达到较高的精度。
然而磁悬浮轴承转子系统的非线性影响因素是不可忽视的,此外,基于漏磁及磁饱和等影响因素的磁悬浮轴承支承特性的研究还比较少。
基于上述原因,综合考虑了软磁材料的磁阻、漏磁等因素的影响并建立了磁悬浮轴承的非线性支承力模型;通过Simulink进行非线性系统在单自由度方向上的动态仿真,对考虑了非线性影响因素的磁悬浮轴承的支承特性进行了研究。
2 线性支承力模型
研究磁极分布为NNSS 型的八磁极主动磁悬浮轴承。磁悬浮轴承的结构参数,如表1所示。径向磁悬浮轴承的结构原理图及单极对的等效磁路图,如图1所示。图中:D—定子内径;g—气隙长度;h和Wp—磁极高度和宽度;Wy—磁轭宽度;Wr—转子磁路宽度;F1和F2—线圈的磁动势;Rg1和Rg2—一个极对中两个磁极的气隙磁阻,Rk—漏磁磁阻,Ry,Rp和Rr—定子磁轭、磁极和转子的磁阻。
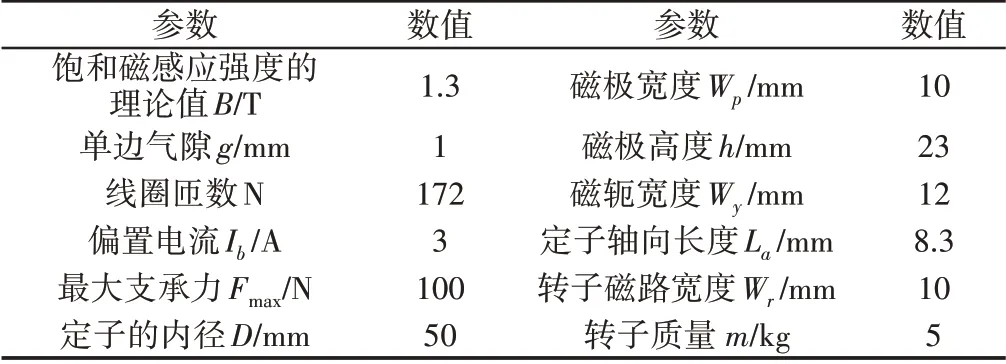
表1 磁悬浮轴承结构参数Tab.1 Parameters of Magnetic Bearing

图1 磁悬浮轴承结构简图和单极对的等效磁路图Fig.1 Schematic Diagram of Magnetic Bearing and Equivalent Magnetic Circuit Model of One Pole−Pair
图1(a)所示的径向磁悬浮轴承的结构可以解耦为水平方向和垂直方向之间的磁耦合,为了简化分析,以竖直方向上单自由度磁悬浮轴承系统为例,考虑到磁悬浮轴承采用差动励磁的方式,可得到磁悬浮轴承线性支承力模型为上下磁极对转子产生的吸力之差[2],即:
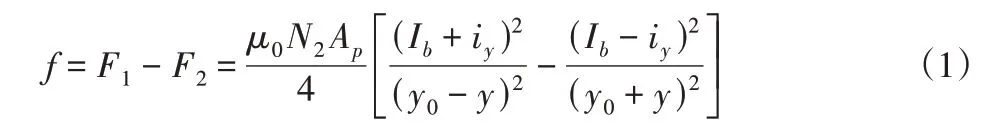
式中:Ib—线圈偏置电流;iy—线圈控制电流;y0—平衡位置时的气隙;y—相对平衡位置的位移。
3 非线性支承力模型
根据图1(b)采用等效磁路法建立磁悬浮轴承非线性支承力模型[9−10],得上下电磁铁对转子合力的一般表达式为:
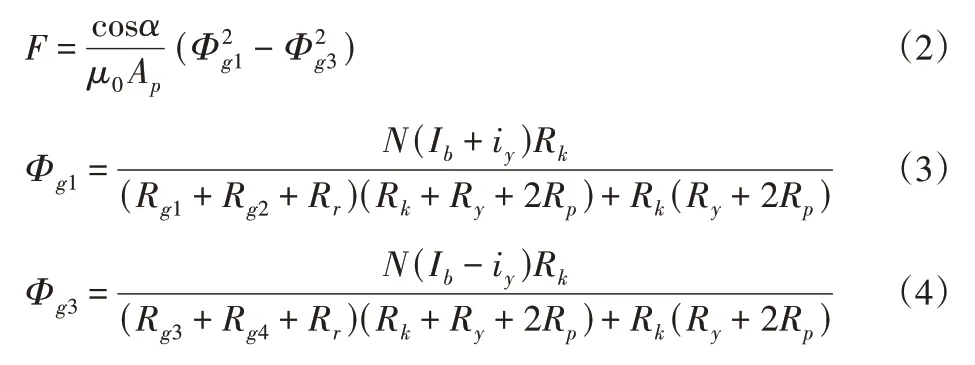
式中:Φg1和Φg3—穿过上极对和下极对的磁通量;μ0—真空磁导率;Ap—磁极面积;Ib—线圈偏置电流;iy—线圈控制电流;Rg3和Rg4—另一极对的气隙磁阻。
3.1 气隙磁通模型
采用磁场划分法[11],首先确定了磁极间气隙磁场的分布规律,将气隙磁场划分为一定形状的磁通管,用解析法计算各磁通管的磁导,最后根据这些磁通管的串联或并联,得到气隙的总磁导或磁阻。将气隙磁场分为磁通管a和磁通管b,磁通管的原理图,如图2(a)所示。假设磁感线是由一系列的圆弧和切线组成,磁感线的一部分穿过气隙流入转子,O点是定子中心,OE是两个相邻磁极的中心线,直线OF是磁极的中心线。
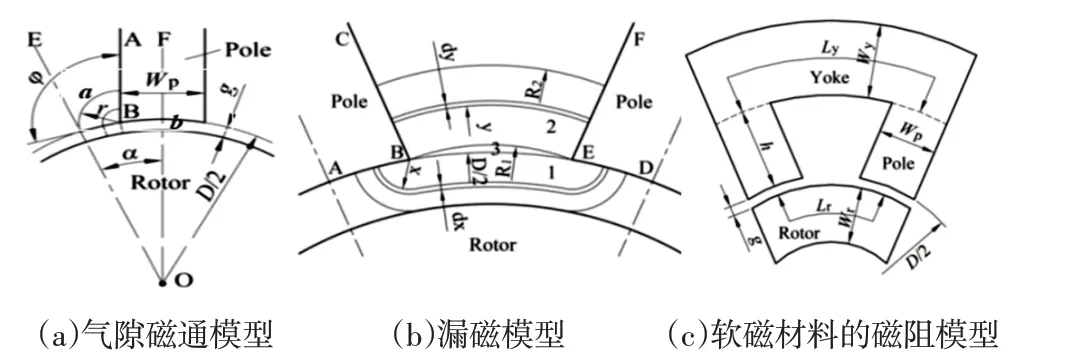
图2 软磁材料的磁通和磁阻模型Fig.2 Models of Magnetic Flux and Reluctances in Soft Magnetic Materials
磁通管a以B点为中心,从AB线开始,在定子内径处终止的弧形磁感线。其中最大半径的弧形磁感线与OE线相切,因此所有的圆弧都不能越过OE线;磁通管b从磁通管a圆弧末端开始,在转子表面终止,恰好是转子与磁极弧面之间的气隙。磁通管a和磁通管b的磁导为:
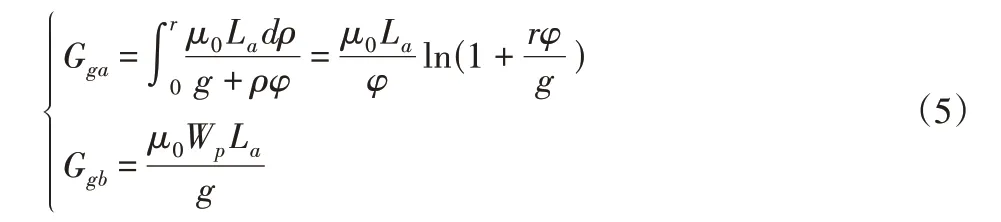
式中:r—最大圆弧的半径;ϕ—圆弧所对应的圆心角。

3.2 漏磁模型
同样将漏磁场划分成磁通管1、磁通管2和磁通管3,如图2(b)所示。
磁通管1的每条路径被认为是由三段弧组成,点B和点E分别为第一段弧和第三段弧的中心,第二段弧平行于转子表面,同时与第一弧和第三弧相切。
磁通管2的路径为环形弧,其公共中心是BC和EF的交点。磁通管1与2之间的面积为磁通管3,呈新月形。
磁通管1、磁通管2和磁通管3的磁导分别为:

式中:R1和R2—环形区域的内半径和外半径;θ1和θ2—新月形内弧与外弧的中心角:

3.3 软磁材料的非线性磁阻
为了考虑磁饱和,对软磁材料的磁阻进行了计算,其中一个极对的几何模型,如图2(c)所示,其中磁极、磁轭和转子的磁阻分别为:
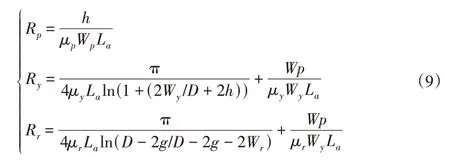
式中:μp、μy、μr—磁极、磁轭和转子的磁导率。
工程实践中软磁材料的外磁场强度约(0~7000)A/m,在此范围内,采用幂函数拟合软磁材料的磁化曲线点[5]。
拟合曲线公式为:

式中:a=−8.253,b=−0.5009,c=1.807。其拟合指数R2—0.9944,拟合精度较高。
根据式(9),磁导率μ和磁感应强度B的关系表示为:

根据饱和磁感应强度计算出磁导率μ,并近似认为磁极、磁轭和转子的磁导率μp、μy、μr都为μ。然后根据式(9)确定相应的软磁材料磁阻,将上述各磁阻代入式(2)~式(4),可得到了磁悬浮轴承的非线性支承力的数学模型。
同时定义磁悬浮轴承的支承刚度K为某方向上单位位移变化所需支承力的增量,定义磁悬浮轴承的电流刚度Ki为单位电流变化所需支承力的增量,即为:

有限元模型考虑了磁悬浮轴承的漏磁及磁饱和的现象,其计算结果更接近磁悬浮轴承的实际情况,以下将以有限元的计算结果作为参考[6,10]。
分别使转子偏离磁悬浮轴承中心0mm、0.025mm和0.150mm,非线性模型、线性模型和有限元模型在这三种偏离位置下的支承力曲线,如图3所示。

图3 不同偏离位置下支承力对比Fig.3 Comparison of Bearing Capacity at Different Deviation Positions
由图3可得知,选择不同的模型时系统的支承特性有较大的区别,非线性支承力模型与有限元模型的相似度较好,因此考虑了非线性因素的非线性支承力模型具有更高的精度,更能满足实际情况的描述。
由以上分析可知,两种模型支承特性的区别主要发生在系统控制电流过大和转子偏离轴承中心这两种情况,因此,以下将基于非线性支承力模型,通过simulink搭建仿真模型,对系统在这两种情况下进行磁悬浮轴承转子系统的动态仿真,分析在非线性因素影响下磁悬浮轴承的支承特性。
4 磁悬浮轴承非线性特性仿真分析
磁悬浮轴承是一个典型的非线性系统,以磁悬浮轴承在垂直方向上的控制系统为例,研究在非线性因素影响下磁悬浮轴承的支承特性。单自由度磁悬浮轴承控制系统由位移传感器Gs(s)、控制器Gc(s)、功率放大器Gp(s)和被控对象模型G(s)等组成。其Simulink仿真模型,如图4所示,取比例系数kp=3.5,积分系数为ki=300,微分系数为kd=0.016,微分时间常数Td=2×10−5;传感器增益As=8000;滞后时间常数Ts=5×10−4;功放增益以Aa=0.6;衰减时间常数Ta=2×10−5。

图4 单自由度磁悬浮轴承的Simulink仿真模型Fig.4 Simulink Simulation Model of Single−Degree−of−Freedom Magnetic Bearing
4.1 系统处于较大控制电流时的研究
现对转子在平衡点附近(y≈0)但控制电流较大的情况进行分析。无负载时,此时两种模型在稳定时的控制电流非常小,在系统稳定后给线性模型和非线性模型都施加0.5A的直流扰动,两种模型的支承力、支承刚度K和电流刚度Ki,如表2所示。
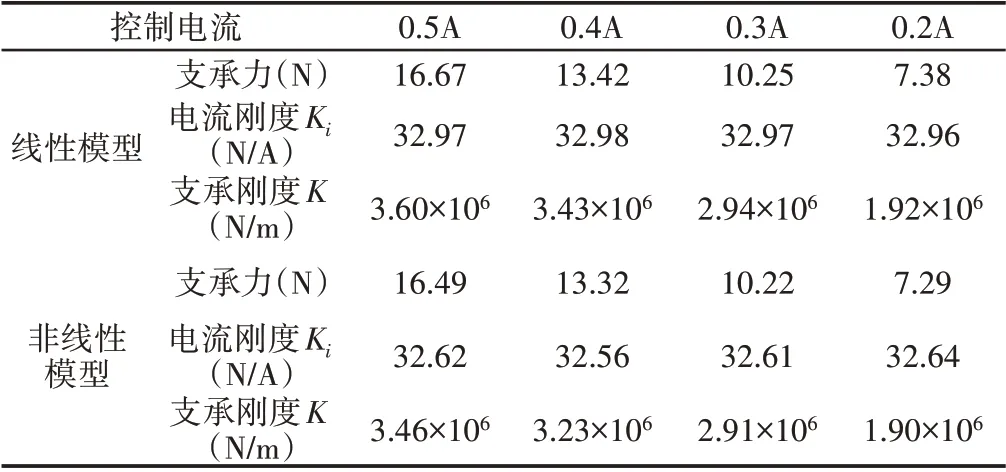
表2 控制电流较小时两种模型的数据对比Tab.2 Data Comparison of Two Models with Small Control Current
此时转子位移响应,如图5(a)所示。支承力变化,如图6(a)所示。两种模型都施加60N的负载,此时两种模型在稳定时的控制电流较大,系统稳定后再给两种模型都施加0.5A的直流扰动,两种模型的支承力、支承刚度K和电流刚度Ki,如表3所示。此时转子位移响应,如图5(b)所示。支承力变化,如图6(b)所示。根据定义和式(11),电流刚度Ki可判断系统是否出现了非线性及支承力随电流变化速度的快慢。

表3 控制电流较大时两种模型的数据对比Tab.3 Data Comparison of Two Models with Large Control Current

图5 两种模型的转子位移响应图Fig.5 Comparison of Rotor Displacement Rresponse of the Two Models
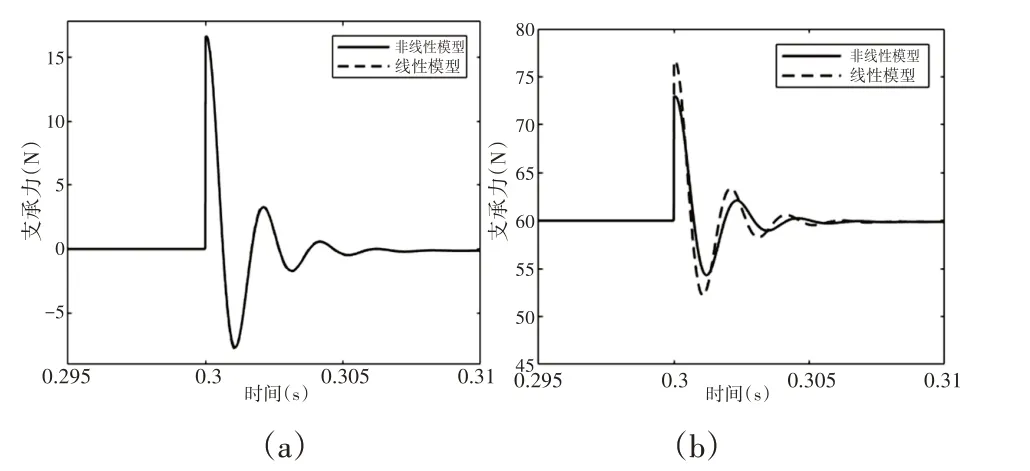
图6 两种模型支承力变化图Fig.6 Changes in Bearing Capacity of the Two Model
从图5(a)和图6(a)可知,当控制电流非常小时,两种系统的动态响应和支承力变化基本一样;由图5(b)和图6(b)可知,当控制电流较大时,相较线性系统,非线性系统响应的最大幅值增加了7.8%,达到最大幅值的时间增加了10.8%,支承力变化速度更慢且最大支承力减小了5%。具体从表2和表3可知,当控制电流较小时,采用两种支承力模型的系统表现基本一样;当控制电流较大时,采用非线性支承力模型的系统提供的支承力和支承刚度更小。随着控制电流的增大,两种模型的支承力之差也越来越大(在0.5A时相差1.02%,在2.3A时相差8.52%)。
造成这种结果的主要原因是系统控制电流越大,非线性因素的影响越大,因此考虑了非线性因素的磁悬浮轴承系统在抵御干扰时的支承表现较差。
通过仿真分析可知,即使转子在平衡点附近,但随着控制电流的增大,非线性因素的影响不可忽视,如果外界干扰造成控制电流过大,考虑了非线性因素的磁悬浮轴承系统将无法提供足够的支承刚度而率先失稳。因此采用非线性支承力模型对磁悬浮轴承系统的实际工作状况更具有指导意义。
4.2 转子偏离轴承中心的研究
现对转子偏离平衡点的情况进行分析。使非线性系统转子分别偏离中心位置0.150mm 和0.025mm,记录为位置一和位置二。两种偏离位置下的转子位移响应,如图7所示。两种偏离位置下的动态响应指标,如表4所示。两种偏离位置下非线性模型的支承刚度K和电流刚度Ki,如表5所示。
从图7、表4和表5可以看出,当转子偏离磁悬浮轴承中心较远时,系统的动态响应出现了恶化,其主要原因是转子在偏离较远位置的过程中,系统的支承刚度不足而导致的。在控制电流较小时,两种偏离位置下系统的支承刚度相差较小(如在0.50A时相差64.71%);在电流很大时,两种偏离位置下系统的支承刚度则相差很大(如在3.0A时相差207.69%)。

图7 两种偏离位置下转子位移响应Fig.7 Comparison of Rotor Displacement Responses at Two Different Positions

表4 不同偏离位置下系统动态响应指标Tab.4 System Response Index at Different Deviation Positions

表5 非线性模型在不同偏离位置下的数据对比Tab.5 Data Comparison of Nonlinear Models at Different Deviation Positions
通过仿真分析可知,转子发生偏移会造成控制电流增大而导致非线性因素的影响加重。转子偏离轴承中心越远,漏磁及磁饱和现象会更严重,此时系统能提供的支承刚度更小,因此系统的超调量和调整时间等动态响应变差。如果转子偏离轴承中心太远,系统将无法提供足够的支承刚度而失稳。
5 小结
通过磁场分割法,建立了考虑漏磁及磁饱和的非线性支承力模型。基于此,采用Simulink搭建了PID 控制仿真模型,对采用非线性支承力模型的磁悬浮轴承系统进行了动态仿真,对于系统控制电流过大和转子偏离轴承中心的这两种情况进行了分析。通过仿真分析可知,当转子在平衡位置附近时,只要控制电流够大,非线性因素就会影响磁悬浮轴承系统的支承特性,考虑了非线性因素的磁悬浮轴承系统提供的支承刚度较小、抵御干扰的能力较差。当转子偏移变大时,会造成系统控制电流增大而导致漏磁及磁饱和会更严重,系统的支承刚度更小,系统的动态响应更差。通过对考虑了非线性因素的磁悬浮轴承系统进行动态仿真分析,可为磁悬浮轴承在非线性下的实际研究提供基础。
