借助图示法巧解两地正午太阳高度差
2023-02-09张明强
张明强
(浙江省新昌中学,浙江 绍兴 312500)
正午太阳高度是指正午太阳光线与地平面的夹角。正午太阳高度角的计算和应用是高中地球运动教学的重点。有关两地正午太阳高度差值变化的规律及其相关题目由于涉及多个变量的计算而成为学习难点。
图示法是用曲线或图形表示数据之间的关系,从图形中能直观反映数据变化的趋势和规律,如递减性或递增性、最大值或最小值,十分适合解决与两地正午太阳高度差值相关的地理问题。由于太阳直射点在南北回归线间做回归运动,两地正午太阳高度差(简称ΔH)必然有明显的季节变化规律和周期性。要想全面总结其变化规律,首先需要分析影响某地正午太阳高度大小的主要因素。
一、正午太阳高度大小的影响因素分析
1.正午太阳高度的计算公式
正午太阳高度H是一天中最大的太阳高度,即为太阳直射点(太阳高度90°)所在经线上所有地点的太阳高度(图1)[1]。图1中A为太阳直射点,纬度为α;B点为直射点所在经线上任意一点,纬度为β。由于太阳光线平行,根据同位角相等可得等式90°-H=β-α,转化后可得H=90°-(β-α)。考虑到当地纬度可能小于直射点纬度,正午太阳高度的公式可概括为:H=90°-|β-α|,其中β为当地纬度,α为直射点纬度(同半球取正值,异半球取负值)。本公式的地理内涵可表述为某地正午太阳高度等于90°减去当地与太阳直射点之间的纬度差。
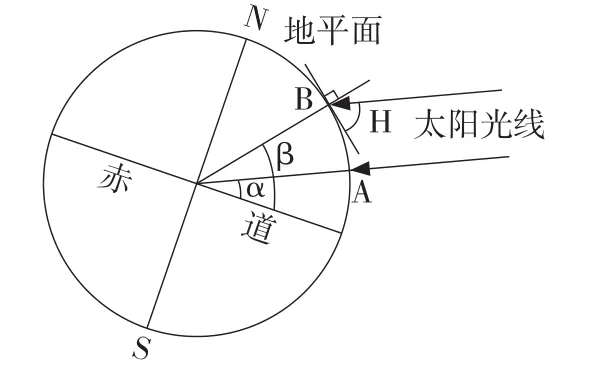
图1 图解法求正午太阳高度示意
2.正午太阳高度的季节变化规律
由于太阳直射点在南北回归线间做回归运动,利用正午太阳高度计算公式可知同一地点正午太阳高度有明显的季节变化规律(图2)。从图2中可以看出,当某地纬度大于或等于23°26′,一个回归年内正午太阳高度只有一次最大值和一次最小值,它们分别出现在夏至日和冬至日。回归线之间的地点一年内有两次直射,出现时间取决于当地的纬度;另外还有一次较小值(太阳直射同半球回归线)和最小值(太阳直射异半球回归线)。赤道一年中正午太阳高度分别在二分日和二至日出现两次直射和二次最小值。
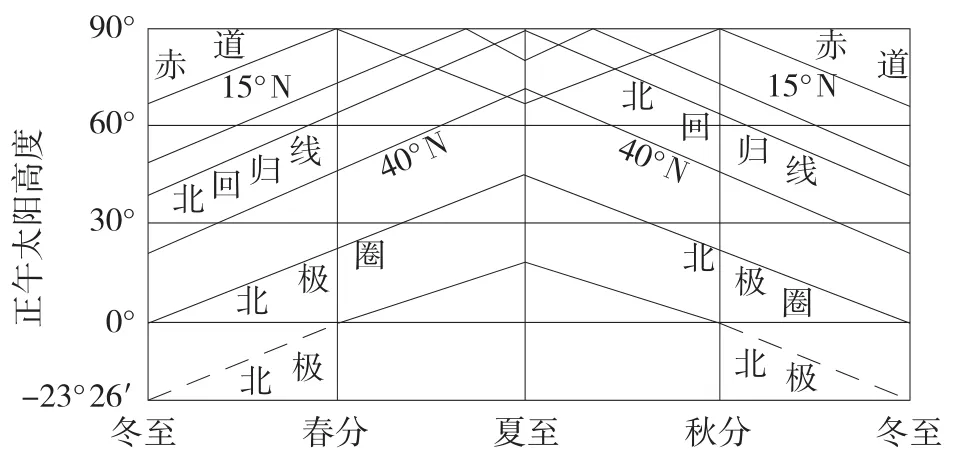
图2 北半球部分地区正午太阳高度的季节变化
综上所述,影响正午太阳高度的因素主要为当地纬度和太阳直射点纬度。若要厘清两地正午太阳高度差值的季节变化规律,首先必须分析两地和太阳直射点之间的纬度差特征,即需要根据两地的纬度位置进行分类讨论。
二、两地正午太阳高度差值的季节变化规律分析
由于太阳直射点的南北回归运动,可以将两地(纬度分别为β和α)按纬度分为回归线与极圈之间和南北回归线之间这两类纬度位置关系(极圈内由于会出现极夜而不予讨论)。两地正午太阳高度差值规律则主要分为以下四种情况。
情况①,两地都位于同半球回归线与极圈之间(包括23°26′和66°34′)。利用正午太阳高度计算公式推断出:两地正午太阳高度随太阳直射点同步增大或减小,其差值ΔH始终保持不变;两地纬度差|β-α|即为两地正午太阳高度差(图3)。
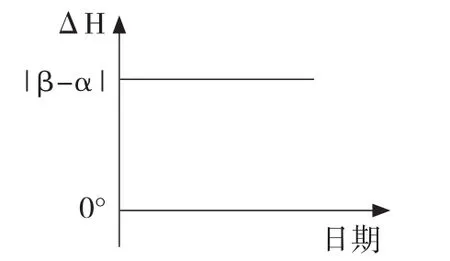
图3 情况①两地正午太阳高度差异示意
情况②,两地分别位于异半球回归线与极圈之间(包括23°26′和66°34′)。利用正午太阳高度计算公式推断出:两地正午太阳高度在夏至日到冬至日期间变化趋势相反,其差值ΔH在逐渐变小,而冬至日到夏至日期间的差值逐渐变大,二至日的正午太阳高度差为极大值和极小值,如图4所示(其中α和β分别表示北半球和南半球两地的纬度,两地正午太阳高度差ΔH=Hα-Hβ,作图时不考虑太阳直射点移动时的速度差异)。通过计算可得极大值为β-α+46°52′、极小值为β-α-46°52′。
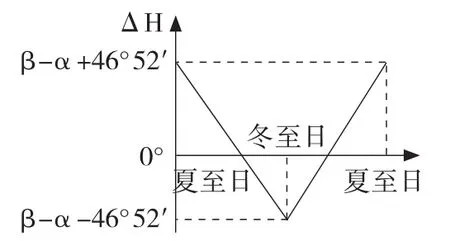
图4 情况②两地正午太阳高度差异示意
情况③,一地位于两回归线之间,另一地位于回归线与极圈之间(包括23°26′和66°34′)。利用正午太阳高度计算公式推断出:当太阳直射点在两地的同侧时,ΔH保持不变,若在两地之间移动时先减小后增大,如图5所示(其中α和β分别表示两回归线之间和回归线与极圈之间的纬度,两地正午太阳高度差ΔH=Hα-Hβ)。图中ΔH是关于夏至日(两地都在北回归线以南)对称的一系列极大值β±α(两地同半球相减、异半球相加);当太阳直射点经过该地后,其差值ΔH先逐渐减小、冬至日后逐渐增大,其中最小值为β±α-46°52′(两地同半球相加、异半球相减)。整体而言,两地正午太阳高度差值变化具有关于二至日对称、有若干时间处于极大值以及只有一个极小值等特征。
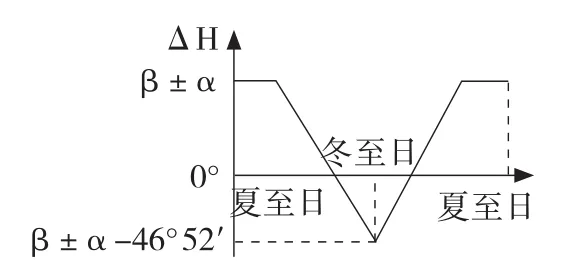
图5 情况③两地正午太阳高度差异示意
情况④,两地都位于南北回归线及其之间。利用正午太阳高度计算公式推断出:当太阳直射点在二至日附近时,ΔH为两地的纬度差|β±α|(同半球相减,异半球相加)或其负数;当太阳直射点在两地之间移动时,ΔH逐渐减小或增大(图6)。
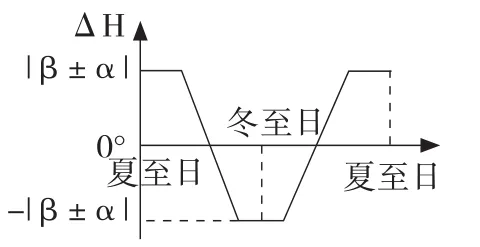
图6 情况④两地正午太阳高度差异示意
综合以上四类情况的分析可以得出以下结论:首先,两地正午太阳高度差ΔH的季节变化规律图都是关于二至日对称的。其次,两地纬度是否小于23°26′决定ΔH的季节变化规律图中的极值分布:当两地纬度都大于或等于23°26′且处于同半球时,ΔH保持不变,而两地位于异半球时,ΔH一年中只有一个极大值和极小值;当两地纬度都小于23°26′时,ΔH一年中有若干个极大值和极小值;而当两地纬度分别小于、大于等于23°26′时,ΔH一年中有若干个极大值和唯一的极小值。
三、两地正午太阳高度差值季节变化规律图在解题中的应用
利用两地正午太阳高度差值的季节变化规律图,结合已知信息可迅速判断出两地纬度特征和特殊日期,这样可省略中间繁杂的讨论过程,直接通过简单的数学计算就能求出具体纬度。如以下例题。
例1.同一经线上的甲、乙两地(其中甲地位于30°N),其连续三个月的正午太阳高度角之差的变化规律如图7所示(回归线纬度取近似值23.5°)。据图完成以下两题。
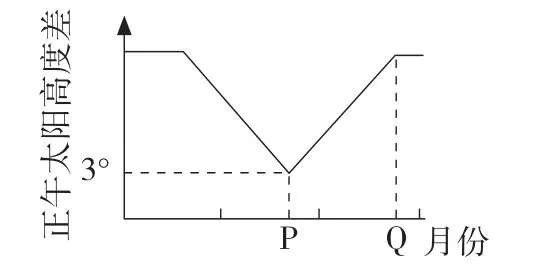
图7 甲、乙两地正午太阳高度差值示意
1.乙地的纬度是
A.14°N B.20°SC.20°N D.56.5°S
2.图中Q点的日期是
A.4月下旬B.7月下旬
C.10月下旬D.2月下旬
【试题品析】图中两地正午太阳高度之差有若干个极大值和唯一的极小值,运用上述四种有关正午太阳高度差的季节变化规律示意图,可直接推断两地中必然有一地纬度小于23.5°,即为乙地。由于甲地位于30°N,所以太阳直射甲、乙之间的北回归线时,正午太阳高度差最小,即夏至日时ΔH=H乙-H甲=3°,又因图中表示连续三个月,所以Q日期对应为太阳直射乙地,即7月下旬,至此可推断乙地位于赤道和北回归线之间。最后通过正午太阳高度计算公式可算出乙地为20°N。
通过以上解析,可以总结出利用两地太阳高度差值特征来计算某地纬度的一般步骤为:第一步,提取题目中有用的文字和图示信息并概括极值特征,调用符合题意的正午太阳高度差示意图判断两地的大致纬度(是否小于23°26′);第二步,根据已知条件综合判断两地所属的半球(确定南纬或北纬);第三步,列出极值点日期对应的有关两地正午太阳高度差的算式,并求出纬度。
