一般图中的最小概要表示集问题*

钟 昊,陈卫东

(华南师范大学计算机学院，广东 广州 510631)

1 引言

给定一个对象集合，任意2个对象之间的相似度越大，表明其中一个对象越能够在一定程度上表示另一个对象。通常根据对象之间的相似度从对象集合中选择一些对象，令这些对象能够概要表示整个对象集合。比如，从知识图谱的摘要模式集中找出一些摘要模式来概要表示整个知识图谱[1]，从文本的句子集合中找出一些句子来概要表示整个文本[2 - 4]。

在一般图中，通常基于图的拓扑结构来刻画任意2个节点之间的相似度。例如，任意2个节点共同位于图中越多数量的增广路径上，节点的相似度越高[5]；任意2个节点之间的连边权重占这2个节点的所有连边权重的比值越大，节点的相似度越高[6]；任意2个节点的共同邻居节点数越多，节点的相似度越高[7]。基于节点的相似度计算方法，从图中选择一些节点来概要表示一个图，被选择的节点称为代表点。由代表点构成的集合满足一些特定条件时，称该集合为概要表示集SRS(Summary Representing Sets)。 本文定义了表示集的2种形式，具体描述为：任意一个由代表点构成的集合被称为概要表示集，当且仅当：

(1)图中任意节点要么属于代表点，要么与该集合中某个代表点的相似度大于或等于给定阈值η∈(0,1)。

(2)图中任意节点要么属于代表点，要么与该集合中所有代表点的相似度之和大于或等于给定的阈值μ∈(0,+∞)。

从图中寻找最少节点数的概要表示集称为最小概要表示集问题，本文对最小SRS问题进行了研究，针对2种形式的最小SRS问题分别进行了形式化的描述，证明任一形式的最小SRS问题都是NP难问题。针对2种形式的最小SRS问题，分别基于次模函数提出一个贪心近似算法进行求解。

2 问题描述

2.1 问题定义

给定一个无向图G=(V,E)，其中,V表示节点集，E表示边集。图G上的一个集合函数s:2V×V→[0,1]是任意2个节点的相似度函数。在图G中，节点的个数n=|V|，边的条数m=|E|。给定一个代表点组成的集合D，任意节点v∈V和子集D中任意代表点的最大相似度为maxu∈Ds(v,u)，和子集D中所有代表点的相似度之和为∑u∈Ds(v,u)。 显然对于任意节点v∈V,maxu∈Ds(v,u)和∑u∈Ds(v,u)关于集合D都是非减的。 下面对最小SRS问题的2种形式进行描述。

(1)给定阈值η∈(0,1)，当任意节点集合D⊆V能够使得∀v∈V满足v∈D或maxu∈Ds(v,u)≥η，那么称集合D为第1种形式的SRS。 第1种形式的最小SRS问题可描述为：从节点集合V中找出最少数量的节点构成集合D，使得∀v∈V满足v∈D或maxu∈Ds(v,u)≥η。

给定阈值μ∈(0,+∞)，当任意节点集合D⊆V能够使得∀v∈V满足v∈D或∑u∈Ds(v,u)≥μ，那么称集合D为第2种形式的SRS。 第2种形式的最小SRS问题可描述为：从节点集合V中找出最少数量的节点构成集合D，使得∀v∈V满足v∈D或∑u∈Ds(v,u)≥μ。

值得一提的是，对于第1种形式的最小SRS问题，当给定的阈值η过大时，对于任意节点v∈V，若其满足不等式maxu∈(V-{v})s(v,u)<η，表示节点v只能被选为代表点。那么设置阈值η过大时可能存在所有节点都只能被选为代表点的情况。为了避免出现上述情况，通常设定阈值η∈(0,minv∈Vmaxu∈(V-{v})s(v,u)]。对于第2种形式的最小SRS问题，当给定的阈值μ过大时，对于任意节点v∈V，若其满足不等式∑u∈(V-{v})s(v,u)<μ，表示节点v只能被选为代表点。那么设置阈值μ过大时可能存在所有节点都只能被选为代表点的情况。同理，为了避免出现上述情况，通常设定阈值μ∈(0,minv∈V∑u∈(V-{v})s(v,u)]。

2.2 问题的计算复杂性

定理1求解最小SRS问题是NP难的。

证明由于最小支配集问题是NP难问题，下面只需证明可将最小支配集问题归约到最小SRS问题。

首先，给出最小支配集问题到第1种形式的最小SRS问题的归约证明。给定任意无向图G=(V,E),设定阈值η=0.5，构造一个节点相似度函数s:2V×V→[0,1]如式(1)所示：

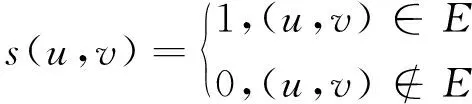
(1)

这个构造显然能在O(n2)的多项式时间内完成，且D⊆V是图G的一个支配集当且仅当D是图G在该相似度函数s下的一个第1种形式的SRS。即，最小支配集问题的任一实例可多项式归约为第1种形式的最小SRS问题的实例求解。

其次，给出最小支配集问题到第2种形式的最小SRS问题的归约证明。注意，在上述归约中，如果设定阈值μ=0.5，则D⊆V是图G的一个支配集图当且仅当D是图G在该相似度函数s下的一个第2种形式的SRS。即，最小支配集问题的任一实例可多项式归约为第2种形式的最小SRS问题的实例求解。

证毕。

3 贪心近似算法

在介绍求解最小SRS问题的贪心近似算法之前，先回顾一下组合优化中NP难的最小基数次模覆盖问题及其贪心近似算法。给定一个有限簇集合U和一个集合函数f:2U→R+，对于任意子集S⊆U，元素i∈(U-S)在S上的边际效益用Δif(S)表示，定义如式(2)所示:

Δif(S)=f(S∪{i})-f(S)

(2)

函数f是次模函数，是指对于任意A⊆B⊆U和任意i∈(U-B)，函数f满足式(3):

Δif(A)≥Δif(B)

(3)

设函数f是正规化的(f(∅)=0)、单调的(任意A⊆B⊆U满足f(B)≥f(A))和次模的，最小基数次模覆盖问题可描述为：找出基数最小的子集S⊆U使得f(S)=f(U)，形式化表示如式(4)所示:

minS⊆U{|S|:f(S)=f(U)}

(4)

最小基数次模覆盖问题及其近似求解算法已经被广泛地应用于图的许多问题中，比如，图的最小支配集问题及其若干变体[8 - 10]、图的最小分辨集问题[11,12]和图的最小边度量维数问题等[13]。求解最小基数次模覆盖问题的一个经典算法：初始化设置一个集合S为空集，依次从U-S中选择使Δif(S)最大的元素i加入到集合S中，直至f(S)=f(U)。求解最小基数次模覆盖问题的贪心算法GAMCSC(Greedy Algorithm for the Minimum Cardinality Submodular Cover problem)的伪代码如算法1所示：

算法1GAMCSC算法

输入:有限簇集合U和集合函数f:2U→R+。

输出:最小基数次模覆盖问题的一个解S。

S←∅;

Whilef(S)

Chooseu∈(U-S) to maximizef(S∪{u});

SetS←S∪{u};

OutputD;

算法GAMCSC已经被证明是近似算法[14,15]。给出2个已有的定理。

定理A若算法GAMCSC对应的势函数f是一个整数型函数，那么算法的近似比为H(α)≤(1+lnα)，其中,H为调和级数,α=maxu∈UΔuf(∅)为势函数f的最大边际效益。

定理B若算法GAMCSC对应的势函数f是一个实数型函数，那么算法的近似比为：(1)1+ln(α/β)，其中β为势函数f的最小边际效益;(2)1+ln(f(U)/opt)，当β≥1，其中opt为最小基数次模覆盖问题的最优解基数。

上述定理将用于证明本文提出的求解最小概要表示集问题的贪心算法的近似比。

3.1 算法描述和近似比证明

在介绍求解第1种形式的最小SRS问题的贪心近似算法前，本文首先定义一个函数t:2V→R+并对于任意子集D⊆V进行以下约定：

(1)对于∀v∈D，令tD(v)=0;

(2)对于∀v∈(V-D)，令tD(v)=max(0,η-maxu∈Ds(v,u))。

在这种约定下，对于∀v∈V，其tD(v)关于D是非增的，表示∀v∈V被选为代表点或满足maxu∈Ds(v,u)≥η时都有tD(v)=0。紧接着，对于任意子集D⊆V，本文考虑一个势函数f1:2V→R+如式(5)所示:

(5)

引理1势函数f1(D)的一些性质：

(1)f1(D)是正规化的、单调非减的次模函数。

(2)当D是一个第1种形式的SRS时，f1(D)=nη。

(3)若f1(D)0。

证明(1)显然f1(∅)=0。由tD(v)=max(0,η-maxu∈Ds(v,u))可知tD(v)关于D是非增的，那么f1(D)关于D是非减的。要证明f1(D)是次模函数，只需证明对于任意A⊆B⊆V和任意x∈(V-B)，势函数f1满足Δxf1(A)≥Δxf1(B)，由式(5)可计算式(6)和式(7)：

(6)

(7)

显然tA(x)≥tB(x)以及(V-A)⊆(V-B)，则只需证明(tA(v)-tA∪{x}(v))≥(tB(v)-tB∪{x}(v))如下：

若tA∪{x}(v)>0且tB∪{x}(v)>0，则式(8)成立：

tA(v)-tA∪{x}(v)=

max(0,s(x,v)-maxu∈As(u,v))≥

max(0,s(x,v)-maxu∈Bs(u,v))=

tB(v)-tB∪{x}(v)

(8)

若tA∪{x}(v)>0且tB∪{x}(v)=0，则式(9)成立：

tA(v)-tA∪{x}(v)=

max(0,s(x,v)-maxu∈As(u,v))≥

max(0,s(x,v)-maxu∈Bs(u,v))≥

max(0,η-maxu∈Bs(u,v))=

tB(v)-tB∪{x}(v)

(9)

若tA∪{x}(v)=0，则式(10)成立：

tA(v)-tA∪{x}(v)=

max(0,η-maxu∈As(u,v))≥

max(0,η-maxu∈Bs(u,v))=

tB(v)-tB∪{x}(v)

(10)

综上所述，Δxf1(A)≥Δxf1(B)是成立的。

(2)若D是一个第1种形式的SRS，那么∀v∈(V-D)都满足tD(v)=0，即f1(D)=nη。若D不是一个第1种形式的SRS，那么存在v∈(V-D)满足tD(v)>0，即f1(D)

(3)若f1(D)0，此时若从V-D中选择节点u加入到集合D中，且节点u满足s(u,v)>maxw∈Ds(w,v)，那么tD∪{u}(v)f1(D)。

证毕。

对于任意子集D⊆V，引理1证明了势函数f1(D)是一个正规化的、非减的次模函数，且势函数f1(D)还是一个实数型函数，那么采用算法GAMCSC的贪心思想求解第1种形式的最小SRS问题，即算法GAMCSC的输入为集合函数f1:2V→R+。本文将基于定理B证明算法GAMCSC是求解第1种形式的最小SRS问题的一个近似算法。

定理2当算法GAMCSC中的输入为集合函数f1:2V→R+时，算法GAMCSC是求解第1种形式的最小SRS问题的一个近似算法，近似比为(1+ln((η+θ)/ϑ))，其中θ表示任意节点和其他节点的最大相似度之和，即θ=maxu∈V∑v∈(V-{u})s(u,v),ϑ表示任意节点v∈V在满足tD(v)>0的前提下最小的tD(v)值，即ϑ=minv∈V,D⊆V{tD(v)|tD(v)>0}。

证明引理1证明了势函数f1(D)是一个正规化的、非减的次模函数，且势函数f1(D)还是一个实数型函数。算法GAMCSC的输入为集合函数f1:2V→R+，基于定理B可知，算法 GAMCSC的近似比为1+ln(α/β)，其中α和β分别为势函数f1的最大边际效益和最小边际效益。

根据势函数f1的次模性，即边际效益递减规律，可计算α=maxu∈VΔuf1(φ)≤(η+θ)，其中θ表示任意节点和其他节点的最大相似度之和，即θ=maxu∈V∑v∈(V-{u})s(u,v)。而β≥ϑ，其中对于任意子集D⊆V,ϑ表示任意节点v∈V在满足tD(v)>0的前提下最小的tD(v)值，即ϑ=minv∈V,D⊆V{tD(v)|tD(v)>0}。综上所述，算法GAMCSC是求解第1种形式的最小SRS问题的一个近似算法,近似比为(1+ln((η+θ)/ϑ))。

证毕。

在介绍求解第2种形式的最小SRS问题的贪心近似算法前，本文首先定义一个函数p:2V→R+并对于任意子集D⊆V进行以下约定：

(1)对于∀v∈D，令pD(v)=0;

(2)对于∀v∈(V-D)，令pD(v)=max(0,μ-∑u∈Ds(v,u))。

在这种约定下，对于∀v∈V，其pD(v)关于D是非增的，表示∀v∈V被选为代表点或满足∑u∈Ds(v,u)≥μ时都有pD(v)=0。接下来，对于任意子集D⊆V，本文考虑一个势函数f2:2V→R+如式(11)所示:

(11)

引理2势函数f2(D)的一些性质：

(1)f2(D)是正规化的、单调非减的次模函数。

(2)当D是一个第2种形式的SRS时，f2(D)=nμ。

(3)若f2(D)0。

证明(1)显然f2(∅)=0。由pD(v)=max(0,μ-∑u∈Ds(v,u))可知pD(v)关于D是非增的，那么f2(D)关于D是非减的。要证明f2(D)是次模函数，只需证明对于任意A⊆B⊆V和任意x∈(V-B)，势函数f2满足Δxf2(A)≥Δxf2(B)，由式(11)可计算式(12)和式(13)：

(12)

(13)

显然pA(x)≥pB(x)以及(V-A)⊆(V-B)，则只需证明(pA(v)-pA∪{x}(v))≥(pB(v)-pB∪{x}(v))如下：

若pA∪{x}(v)>0且pB∪{x}(v)>0，则式(14)成立：

pA(v)-pA∪{x}(v)=s(x,v)=

pB(v)-pB∪{x}(v)

(14)

若pA∪{x}(v)>0且pB∪{x}(v)=0，则式(15)成立：

pA(v)-pA∪{x}(v)=s(x,v)≥

max(0,μ-∑u∈Bs(u,v))=pB(v)-pB∪{x}(v)

(15)

若pA∪{x}(v)=0，则式(16)成立：

pA(v)-pA∪{x}(v)=max(0,μ-∑u∈As(u,v))≥

max(0,μ-∑u∈Bs(u,v))=pB(v)-pB∪{x}(v)

(16)

综上所述，Δxf2(A)≥Δxf2(B)是成立的。

(2)若D是一个第2种形式的SRS，那么∀v∈(V-D)都满足pD(v)=0，即f2(D)=nμ。若D不是一个第2种形式的SRS，那么存在v∈(V-D)满足pD(v)>0，即f2(D)

(3)若f2(D)0，此时若从V-D中选择节点u加入到集合D中，那么∑w∈(D∪{u})s(w,v)>∑w∈Ds(w,v)，即pD∪{u}(v)f2(D)。

证毕。

对于任意子集D⊆V，引理2证明了势函数f2(D)是一个正规化的、非减的次模函数，并且势函数f2(D)还是一个实数型函数，那么采用算法GAMCSC的贪心思想求解第2种形式的最小SRS问题，即算法GAMCSC的输入为集合函数f2:2V→R+。本文将基于定理B证明算法GAMCSC是求解第2种形式的最小SRS问题的一个近似算法。

定理3当算法GAMCSC中的输入为集合函数f2:2V→R+时，算法GAMCSC是求解第2种形式的最小SRS问题的一个近似算法,近似比为(1+ln((μ+θ)/ρ))，其中θ表示任意节点和其他节点的最大相似度之和，即θ=maxu∈V∑v∈(V-{u})s(u,v),ρ表示任意节点v∈V在满足pD(v)>0的前提下最小的pD(v)值，即ρ=minv∈V,D⊆V{pD(v)|pD(v)>0}。

证明引理2证明了势函数f2(D)是一个正规化的、非减的次模函数，且势函数f2(D) 还是一个实数型函数。算法GAMCSC的输入为集合函数f2:2V→R+，基于定理B可知，算法 GAMCSC的近似比为1+ln(α/β)，其中α和β分别为势函数f2的最大边际效益和最小边际效益。

根据势函数f2的次模性，即边际效益递减规律，可计算α=maxu∈VΔuf2(∅)≤(μ+θ)，其中θ表示任意节点和其他节点的最大相似度之和，即θ=maxu∈V∑v∈(V-{u})s(u,v)。而β≥ϑ，其中对于任意子集D⊆V,ρ表示任意节点v∈V在满足pD(v)>0的前提下最小的pD(v)值，即ρ=minv∈V,D⊆V{pD(v)|pD(v)>0}。 综上所述，算法GAMCSC是求解第2种形式的最小SRS问题的一个近似算法，近似比为(1+ln((μ+θ)/ρ))。

证毕。

3.2 算法复杂度

给定一个无向带权图G=(V,E),|V|=n。 假设任意2个节点的相似度已知的前提下，计算任一节点与其他节点的相似度之和的时间复杂度为O(n)，那么计算所有未被选为代表点的节点与其他节点的相似度之和的时间复杂度为O(n2)。 在每一轮代表点的选择过程中，根据被选为代表点时节点势函数的增量大小排序所有非代表点，最小的时间复杂度为O(nlogn)，选择令势函数f的增量最大对应的非代表点作为代表点。贪心算法GAMCSC最多需要挑选n个节点作为代表点，综上所述，贪心算法GAMCSC的时间复杂度为O(n3)。

4 结束语

本文基于节点相似度提出了概要表示集的概念，并分为2种形式进行讨论。本文证明了求解任一形式的最小概要表示集问题都是NP难问题，这表明不太可能存在多项式时间内求解该问题的精确算法。本文基于次模函数提出了2个时间复杂度为O(n3)的贪心近似算法，用于求解2种形式的最小概要表示集问题。