飞行器翼型表面流场数据智能分区*

胡跃迪,苏 想,李 楠,张丽梅

(北京工商大学人工智能学院，北京 100048)

1 引言

随着复杂装备先进设计制造手段的进步与发展，计算流体力学CFD(Computational Fluid Dynamics)的应用越来越广泛[1]，目前，借助高性能计算机系统，可以计算、存储规模巨大且复杂度较高的CFD流场数据[2]。由于设计对象的复杂度增加，CFD仿真产生的流场数精度也在不断提高，因此对流场数据的分析和处理也有越来越高的要求，这为流场数据后处理带来了巨大的挑战。

由于航空航天业的不断发展，飞行器设计的复杂度不断提高，使得飞行器设计的时间周期愈来越长。设计人员在飞行器的气动外形设计和仿真过程中，往往需要根据仿真结果重点分析某一区域而不是整个气动外形的各物理参数计算结果分布情况，并根据分析结果进行设计优化。因此，根据仿真结果的多物理场分布自动化地进行区域划分，找出技术人员需要重点关注的一个或几个区域，使设计师可以对特定的某些流场区域进行更精细的计算，可以在相当程度上提升设计分析迭代过程的自动化程度，进而提升设计的效率和质量。

Figure 1 Overall technology roadmap图1 总技术路线图

在国内，针对流场数据后处理可视化的研究已产生了不少系统级成果，如国家数值风洞项目的 NNW-TopViz(National Numerical Windtunnel-TopViz)流场可视分析系统[3]等。

在基本的流场数据可视化基础上，常常还需要针对后处理数据进行进一步分析和处理。Ströfer等[4]利用循环神经网络识别翼体连接处三维流动中的马蹄涡，将深度神经网络应用在三维流场中。Franz等[5]将卷积神经网络的特征学习与已有的图像处理工具特征跟踪器相结合，提出了一个基于深度学习的涡检测和跟踪框架。针对现有机器学习方法在旋涡提取中存在的训练集本身并不完全准确和准确率评价不够严谨的问题，提出了基于全卷积分割网络的旋涡提取方法，用于检测流场数据中的旋涡结构。

还有研究人员利用语义分割[6,7]等方法对仿真结果进行后处理。姚叶等[8]提出了基于深度学习的流场数据后处理方法，将可视化和对流场数据后处理的机器学习方法结合起来，将三维的流场数据转化为二维的流场图像，再对二维流场图像进行智能分区，分区速度得到了有效的提升。但是，由于在降维的过程中直接舍弃了一个维度的数据，使得新得到的二维流场图像与原三维流场数据相差较大，所以得到的分区结果的正确率也不理想。

根据以上研究，本文针对机翼翼型这一类特定问题，提出了基于参数化算法的流场结果数据降维并智能分区的方法。该方法总体技术思路如图1所示，包含如下4部分：

(1)样本数据集生成：采用参数化批量机翼翼型建模和网格生成技术批量生成待求解网格，再利用CFD数值模拟来批量生成流场数据。

(2)将流场数据重采样并矩阵化：基于参数化算法将3维流场数据映射到二维平面，再把平面三角网格流场数据重采样为矩阵数据。

(3)设计并构建卷积神经网络模型，针对流场数据分区任务进行训练。

(4)通过逆映射将矩阵数据重采样到三维网格，使分区结果在原机翼模型上进行可视化展示。

2 参数化翼型流场数据批量计算

以往构建流场数据集时，一般采用飞行试验，使用真实飞机在真实场景下飞行得到流场数据。如此得到的流场数据清晰准确，但耗时巨大。本文的数据集构建采用CFD数值模拟完成。通过变化仿真前的处理参数，得到大量不同机翼外形的仿真流场数据。参数化数据驱动方式可以使数据集批量化自动生成，提升了数据集的构建效率。

2.1 气动外形参数化批量生成及数值模拟

为了批量生成大量的机翼流场数据以构建数据集，需要使用CFD仿真软件来进行流场数值模拟。数值模拟方法采用基于直角网格的解算器完成。流场数据的生成主要分为3个步骤：网格生成及计算参数设置；直角网格生成；流场计算。针对生成流场数据之前的模型问题，可以通过参数化驱动批量修改气动外形来实现，如图2所示：(1)定义机翼两端面曲线种子点；(2)将种子点拟合成线；(3)通过放映方法将线组合成模型。生成不同的机翼模型后，设置好三角网格密度，然后对机翼模型进行数值计算，得到流场文件。

Figure 2 Parametric generation of wing airfoils图2 参数化生成机翼翼型

2.2 基于参数化的表面三维流场数据降维

由于高维流场数据量大，所以直接对高维流场进行分区处理时，会使处理时间过长，从而影响效率。如果对高维流场进行降维和矩阵化处理，就可以缩短处理时间,提高效率。

为了更直观、清晰地展示流场数据，更方便对流场数据进行后处理，需要提取流场数据中某些重要的数据。流场数据中比较重要的数据就是点(三维空间中的x、y、z轴方向的坐标)、单元(由坐标点形成三角网格)和点上对应的流场数据。所以，需要将这3种数据提取出来组成一个新的网格数据。为了使三维数据降维，需要对数据进行参数化，也就是对生成的网格数据进行表面参数化。通过表面参数化可以将一个立体几何的3D顶点坐标重新编码成2D顶点坐标。从纹理映射到表面重新网格化已经提出了许多参数化算法。

目前，计算共形几何在很多领域中得到了广泛的应用。计算共形几何主要研究保角变换下的不变量和曲面之间的共形映射[9]。为了使得转换后的数据与原数据尽量相同，需要用到共形映射(即保角变换下不变量)，保角映射局部上保持形状(三角面片角度)不变。计算共形几何中的调和映射主要用于计算亏格为零的封闭拓扑球面或者带边界的拓扑圆盘[10 - 12]。调和映射的基本原理是优化调和能量，当调和能量达到最小时，映射就是调和映射。输入一个带边界的拓扑圆盘M:

(1)遍历拓扑圆盘的边界，存储边界点到链表，如式(1)所示：

∂M={v0,v1,…,vn-1}

(1)

(2)计算整个边界的长度，如式(2)所示；

(2)

其中，lvi,vi+1为2点[vi,vj]的长度。

(3)设置边界条件，如式(3)～式(5)所示；

(3)

(4)

f(vi)=(cosθi,sinθi),vi∈∂M

(5)

(4)使用牛顿迭代法优化调和能量,如式(6)所示：

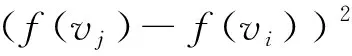
(6)

其中，kij表示调和能量[13]。

调和映射是一种固定边界的参数化算法，算法高效且简单，但相比不固定边界的算法会产生较大的失真。

最小二乘保角参数化LSCM(Least Squares Conformal Maps parametrization)与调和映射不同，它不需要有固定的边界,其中心思想是已知一组点的数据(x,y)，可以近似为线性关系y=ax+b，目标为确定常数a和b，如式(7)所示；

(7)

找到a和b，使得所有yi与axi+b偏差的平方和Q最小。

ARAP(As-Rigid-As-Possible parametrization)是用于计算尽量保持距离(以及角度)的参数化：每个三角形都映射到试图保持其原始形状的平面，直至进行刚性旋转，最后边界可以自由变形，以最小化失真，可以做到保刚性(即保角又保形)。

ARAP变形算法的核心能量函数如式(8)所示，通过最小化该能量函数实现模型的尽可能刚性变形。Ai到Bi进行刚体变换，变换过程中存在旋转矩阵Ri，如式(8)所示：

(8)

其中，Ai和Bi分别表示变形前后模型顶点ai和bi对应的变形单元，N(i)表示ai的1-邻域点的索引，aj和bj分别表示ai和bi的1-邻域顶点，Ri表示Ai到Bi的最优旋转矩阵，Wij是边eij=(ai,aj)的权重[14]。

图3为三维模型经过调和映射，LSCM和ARAP的三角网格角度和坐标点距离变化图。

Figure 3 Changes before and after dimensionality reduction by different parameterization methods图3 不同参数化方法降维前后的变化

坐标点a，b，c和d经过调和映射变为a1，b1，c1和d1，经过LSCM变为a2，b2，c2和d2，经过ARAP变为a3，b3，c3和d3。从图3中可以看出，三维模型经过调和映射后边界处坐标点之间的疏密程度发生的变化大于经过LSCM和ARAP发生的变化。将流场数据重采样为矩阵数据是根据映射后的u和v坐标点进行重采样。为了使重采样后的矩阵数据与原三维流场数据更相近，需要映射前后的坐标点之间的距离变化最小，距离变化是流场数据矩阵化后前后相近程度的重要因素。

LSCM在映射的过程中尽可能地保持三角形的角度相同，ARAP算法在LSCM的基础上尽可能地保证三角形没有扭曲地映射在二维平面上。相比于LSCM，经过ARAP的坐标点与原三维坐标更相近，所以只需要讨论调和映射和ARAP对数据矩阵化的影响，如图4所示。三维流场数据经过调和映射后部分坐标点之间的距离和角度变化较大，将映射后的二维网格数据矩阵化后，可以看出新的矩阵数据分区不均等；三维流场数据经过ARAP后坐标点之间的距离和角度变化较小，将映射后的二维网格数据矩阵化后，可以看出新的矩阵数据分区均等。

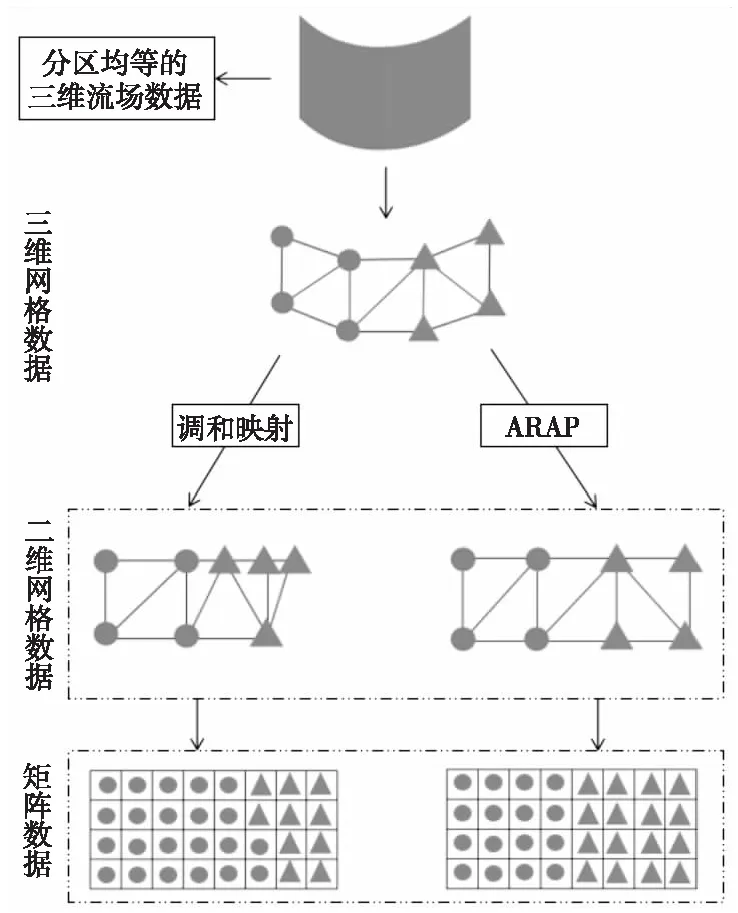
Figure 4 Matrixing with harmonic mapping and ARAP图4 经过调和映射和ARAP的矩阵化

3 非结构化流场数据重采样及矩阵化

由于智能分区模型的输入需要的是结构化的矩阵数据，所以要将非结构化的网格数据重采样为结构化的矩阵数据。流场数据的结构化处理可以在确保流场数据信息变化较小的情况下改变流场的结构形式，使得新产生的流场数据可以作为智能分区模型的输入。对于分析数据而言，非结构化数据的分析工具目前还处于萌芽和发展阶段，而对于结构化数据已有成熟的分析工具，所以有必要将流场数据进行结构化处理。

3.1 三角网格流场数据矩阵化方法

由于得到的流场数据分布在点上而不是单元上，所以先考虑点的位置和点对应的流场数据。在矩阵化时，先重采样点的位置，然后在重采样后的格点上填上对应的流场数据。

经过降维后的三角网格数据可以看成一个平面(u,v)坐标系上的点，将u，v坐标上的点重采样到三维矩阵AM×N×P上。先找到(u,v)坐标系对应的矩阵格点位置，如式(9)和式(10)所示：

(9)

(10)

其中，m，n分别为矩阵格点的行和列的位置；M，N分别为矩阵的行数和列数,(x,y)为u,v坐标系上的点。

图5为矩阵化算法流程图。图6是三角网格数据矩阵化示意图，最后得到的是重采样后的三维矩阵可视化的效果。为了使数据矩阵化过程中的误差最小，需要保证流场数据上所有的坐标点都有相对应的矩阵格点位置。

Figure 5 Flow chart of matrixing algorithm 图5 矩阵化算法流程图

Figure 6 Matrixing of triangular mesh data图6 三角网格数据矩阵化

3.2 矩阵数据去稀疏化方法

上文得到的矩阵数据可视化后会发现重采样后的矩阵数据太稀疏，流场数据所对应的格点分布不密集。为了使重采样后的矩阵数据和原流场数据可视化效果相近，需要对矩阵数据进行去稀疏化处理。遍历矩阵的每个格点，使得矩阵每个格点上的元素都为流场数据。去稀疏化时需要考虑2种情况，一种是矩阵中存在流场数据的格点间隔比较远，整个矩阵中较稀疏的部分；另一种是矩阵中存在流场数据的格点间隔比较近，矩阵中较密集的部分。

图7为矩阵数据去稀疏化示意图，x为流场数据。处理较稀疏区域：对x1所在的格点进行处理，当半径为R的区域内没有流场数据后将x1填入半径为r所在的区域。处理较密集区域：对没有流场数据的格点进行处理，找到无流场数据的格点后，以该格点为圆心，一个格点间距为半径，按顺时针旋转，将碰到的第1个有流场数据格点上的数据填到圆心处，依次遍历所有无流场数据的格点，最终完成去稀疏化处理。

Figure 7 Matrix data de-sparse图7 矩阵数据去稀疏化

Figure 8 Flow chart of matrix data de-sparse algorithm 图8 矩阵数据去稀疏化算法流程图

图8为矩阵数据去稀疏化算法流程图。对于稀疏的部分：遍历矩阵数据中所有元素是流场数据的格点，以这些格点为圆心，不同的R(R=2r，r∈N，r<5)值为半径画圆(如果r太大，形成的圆区域过大，区域格点上肯定存在流场数据，所以要将r设置得小一点)，组成新的格点区域，如果除圆心处的格点外其他所有格点上的元素都不是流场数据，则将半径为r的圆区域格点上的所有元素都换成圆心处的格点上的流场数据。对于密集的部分：遍历矩阵数据中所有元素不是流场数据的格点，以这些格点为圆心，b(b=1，2)为半径(经过第1部分处理后矩阵数据中的元素大部分已经变为流场数据，遍历完以2为半径的圆区域后，所有格点就都可以被流场数据赋值)，顺时针或逆时针遍历每个格点，将碰到的第1个为流场数据的元素赋值到圆心处的格点上。

4 基于卷积神经网络的流场分区模型

4.1 分区模型结构

在深度神经网络中，卷积网络可以进行特征提取，因此可以利用多层卷积神经网络来实现特征提取，得到足够多的特征后再对这些特征进行反卷积，使经过卷积层缩小的数据还原成原来的大小。通过主干特征提取部分获得初步的有效特征层；再通过加强特征提取网络对得到的初步有效特征层进行上采样、堆叠和特征融合，获得最终的特征层；通过卷积最后的特征层进行通道调整，对数据进行智能分区操作[15]。网络模型结构如图9所示：(1)进行2次3×3的64通道的卷积和1次2×2最大池化；(2)进行2次3×3的128通道卷积和1次2×2最大池化；(3)进行2次3×3的256通道卷积和1次2×2最大池化；(4)进行2次3×3的512通道卷积和1次2×2反卷积；(5)与之前得到的128×128×256矩阵拼接后进行2次3×3的256通道卷积和1次2×2反卷积；(6)与之前得到的256×256×128矩阵拼接后进行2次3×3的128通道卷积和1次2×2反卷积；(7)与之前得到的512×512×64矩阵拼接后进行2次3×3的64通道卷积和1次1×1卷积，以进行通道调整。

基于卷积神经网络学习的特征是翼型表面物理场的物理信息经过降维变化和重采样后形成的特征图。通过寻找多物理场中区域与区域之间的边界特征，可以根据这些重要的物理量进行区域划分,使卷积神经网络更容易对数据进行分区处理。

Figure 9 Structure diagram of the proposed model图9 模型结构图

本文数据集是通过直角网格结算器的Piflow软件批量仿真出来的翼型流场数据。流场数据经过降维和矩阵化后得到矩阵数据，然后再对矩阵数据进行手工标记以划分流场区域，得到供实验用的数据集。其中数据集的90%用于训练，剩余的10%用于测试，最后得到的测试精度为92.62%，测试结果如表1所示。

Table 1 Test accuracy of the proposed model

4.2 分区结果逆映射

流场数据经过卷积神经网络进行分区后得到的分区结果是计算结果的特征分区，需要将得到的结果通过逆映射重采样到三维坐标点上，才能使分区结果在原机翼翼型上进行可视化展示。

图10为逆映射算法流程图。图11为矩阵数据逆映射示意图。在数据矩阵化时对矩阵中元素为流场数据的格点进行标记；将标记后的位置与分区后的矩阵数据进行比较，找到重合的格点位置上对应的坐标点；再用坐标点组成新的三维模型。

Figure 10 Flow chart of inverse mapping algorithm 图10 逆映射算法流程图

Figure 11 Matrix data inverse mapping图11 矩阵数据逆映射

流场数据分区结果的可视化效果对比如图 12所示，图12a为Piflow生成的流场数据，图12b为手工分区后的流场数据，图12c为经过本文方法智能分区后的三维分区区域与原机翼模型叠加的可视化效果图。其中，第1个机翼模型有5 309个坐标点，手工标记的分区区域内有777个坐标点，经过实验后的分区区域内有693个坐标点，正确率为89.2%；第2个机翼模型有7 424个坐标点，手工标记的分区区域内有1 208个坐标点，经过实验后的分区区域内有1 064个坐标点，正确率为88.1%。

Figure 12 Comparison chart of airfoil partition 图12 流场分区对比图

5 结束语

本文提出的翼型流场数据智能分区方法，为流场数据的后处理和翼型设计进一步优化提供了参考。参数化批量翼型生成及数值模拟能够有效生成翼型训练数据集。采用参数化方法，能够有效进行流场数据降维。通过对流场数据进行矩阵化，可以使二维流场数据转化为矩阵数据，转化后的矩阵数据可以作为预测模型的标准输入。提出的翼型分区卷积神经网络模型能够有效完成分区任务，测试精度达到92%以上。同时,采用数据逆映射算法可有效地将矩阵数据重采样到三维表面。

对于流场数据的智能分区而言，本文方法的不足之处在于对处理的流场数据的复杂度有所欠缺。对复杂的模型而言，参数化降维比较困难，降维后产生的误差相对较高。但是，在处理简单模型时，如机翼等，参数化降维过程中产生的误差较小，对分区的结果影响不大。针对这些不足，后续工作将对参数化方法进行改进。