同时取送货配送路径优化的两阶段混合策略搜索算法

徐 宁，胡义秋，姚 康（南京审计大学 商学院，江苏 南京 210029）

0 引言

车辆同时取送货是物流企业在配送环节提高运作效率所需要采用的重要模式，通过将集货与配货结合起来可以合理利用配送途中车辆剩余载荷。配送中实现同时取货与送货作业可以有效结合再制造与资源的回收利用，降低企业的配送成本。该模式下的路径优化问题具有高复杂度和难以求解的特点，同时求解过程需要面临时间效率、运作成本的兼顾。

同时取送货问题是传统车辆路径问题的延伸，扩展了车辆路径问题的使用场景，近些年越来越多的学者对其展开研究。Hu 等考虑了动态且取货与送货不相容的VRPSPD 问题[1]，为管理者解决货物不相容的取送货问题提供了定量的依据；Wang 等考虑了时间窗[2]，构建了多目标优化模型，并以实际业务数据证明了所设计的多目标邻域搜索算法的有效性；马艳芳等考虑了运行环境的不确定性构建了不确定VRPSPD 数学模型[3]，引入模糊随机理论描述决策环境中的不确定性；Hornstra 等研究了考虑货物装卸后进先出原则的同时取送货车辆路径问题[4]；Zhang 等研究了新加坡快时尚商品的多种类商品需求的同时取送货问题[5]，并通过自适应内存优化策略求解超过10 000 个节点的大规模实际问题；Büsta 等以最小化燃油消耗为目标[6]，建立了绿色取送货车辆路径问题的整数线性规划模型，并设计了超启发式算法对其进行求解；Golsefidi 等针对生产-库存的同时取送货问题提出了一种鲁棒的混合整数线性规划模型[7]，并设计了两种启发式算法用于求解该线性模型；Foroutan 等研究了同时考虑多车型与碳排放的同时取送货路径规划问题[8]，建立了以最小化成本和碳排放的多目标整数线性规划模型。

对于求解同时取送货问题，根据问题的业务场景与客户规模的不同，学者提出了诸多的策略。Soylu 在研究多旅行商问题时设计了变邻域搜索算法[9]，并通过仿真试验验证了算法具有良好的收敛效果；Mu 等设计了并行模拟退火算法用于求解同时取送货车辆路径问题[10]，并通过不同规模算例验证了算法的有效性；Belgin 等设计了变邻域下降与邻域搜索算法求解带同时取送货的两级车辆路径问题[11]，并构建中大规模算例验证算法有效性，通过实例表明文中算法能够有效应用于现实配送场景；裴颂文等采用了一种融合拓展性K-Means++算法和遗传算法的路径动态规划模型（KMG）[12]，实现包含逆向物流的无人机调度策略；Majidi 等设计了自适应大邻域搜索算法用于求解带同时取送货的污染路径问题[13]；Lagos 等设计了改进的粒子群算法对带同时取送货和时间窗的车辆路径问题进行了求解[14]；Chentli 等设计了自适应大邻域算法用于求解同时取送货的车辆路径问题[15]，并通过多个算例证明了算法的有效性；Qiu 等采用了分支定界的方法求解考虑逆向物流的路径问题[16]，算法在取货量相对较大时更加高效；Zhao 等设计了一种超启发式算法框架用于求解带同时取送货的选址-路径问题[17]，该算法框架在求解质量和速度上均优于传统的算法框架；Ma 等采用基于模糊逻辑控制器和模糊随机仿真的混合优先级嵌套遗传算法求解逆向物流环境下带时间窗和同时取送货的车辆路径问题[18]，并用多个规模算例对算法有效性进行验证；Afra 等在求解取送货问题时考虑了启动成本和环保因素[19]，设计了拉格朗日松弛算法（LR）对其进行求解。客户规模是路径优化问题的重要影响因素之一，随着客户节点的规模增大，精确求解法和传统启发式算法的计算时间呈指数级增长，难以求得较优解。

本文研究较大规模带同时取送货的车辆路径问题，针对规模较大的同时取送货物流配送问题提出了基于“先分解，再求解”思想的两阶段策略，通过聚类方法将规模较大的问题分解为多个小规模的问题，并将每个子问题的规模约束在一辆运输车能满足规模内所有客户需求的范围内，即将子问题转化为求解旅行商问题，再设计混合变邻域搜索算法提高对子问题搜索能力的适应，提高对该类较大规模配送路径问题的求解能力。本文通过不同规模的算例计算，并与同类算法进行对比，验证两阶段的算法能够有效求解同时取送货物流配送问题，为企业在整合取货与送货时合理调配车辆提供方法理论支持。

1 同时取送货物流配送问题描述与数学模型的构建

1.1 同时取送货物流配送问题描述

带同时取送货物流配送规划问题是传统VRP 问题的延展，指配送车辆在对客户执行送货任务时，同时可能有取货需求，这要求车辆需要有效利用配送任务中产生的剩余载荷，在满足容量约束的条件下，规划配送路线，最小化配送成本。同时取送货物流配送问题可以被描述为在欧式平面内的一个全连通图G=｛V,A ｝，顶点集V=｛0,1 ,…,N ｝，其中：0 为配送中心，i（i≠ 0）为客户节点。弧集为A，车辆沿弧（i,j）∈A 的行驶距离为dij。配送中心负责满足N 个客户的送货需求di和取货需求pi，设所有客户的送货与取货需求由配送中心的M 辆运输车负责，运输车完全相同，其固定启动成本为c1，单位距离的运输成本为c2，载荷量为Q，车辆从配送中心出发，负责服务一批客户后回到配送中心，每个客户仅被访问一次，且每个客户的需求都被满足。所有距离都用平面上的欧式距离表示，假设所有车辆的速度为匀速，且严禁超载。同时取送货物流配送问题就是为每辆车找到满足约束且成本最小的路径。同时取送货物流配送网络如图1 所示。

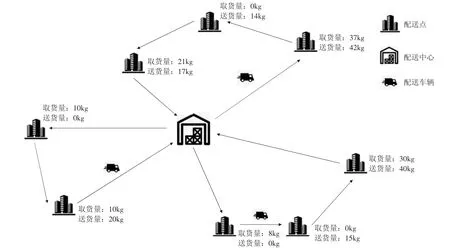
图1 同时取送货物流配送问题示意图

构建模型需满足以下约束：载荷约束，在任何时刻，车辆的载重量不超过车辆的最大载荷；行驶路线，约束车辆从配送中心出发，完成配送任务后返回配送中心；服务次数约束，一个客户节点只能被一辆车服务，一辆车可服务多个客户节点；节点约束，车辆从某个客户节点进入则必须从该节点离开。

1.2 建立同时取送货物流配送问题的数学模型

基于上述问题描述，构建以成本最小化为目标函数的同时取送货物流配送模型：

目标函数式（1）表示最小化配送总成本，第一项为车辆固定启动成本，第二项为车辆的旅行成本；式（2）表示每个客户仅被访问一次，式（3）表示车辆驶入某节点后一定从该点驶出；式（4）表示每辆车最多只被使用一次；式（5）表示每条弧上的取货和送货载荷不超过车辆的额定载荷；式（6）和式（7）表示取货与送货的流量守恒；式（8）表示每条弧上的载荷都大于等于0；式（9）表示若车辆k 经过弧（i,j） ∈A，则为1，否则为0。模型所有的符号定义如表1 所示。

表1 模型中的符号说明

2 求解同时取送货物流配送问题的两阶段策略设计

2.1 区域划分聚类算法

客户节点都为离散的点，本文基于k 均值聚类算法设计区域划分算法（RPC）将配送范围划分为多个区域。聚类属于无监督学习，聚类过程不受限制，由于车辆有载荷约束，因此需对聚类算法增加约束使得每个类中配送需求或取货需求总量都不超过一辆车的载荷能力。算法将客户节点划分为M 个区域，每个区域内的客户满足一辆运输车即可负责服务，从而在每个区域内的路径规划可转化为求解旅行商路径问题。

计算客户的送货总量D 与取货总量P，通过单辆运输车的容量Q，估算满足全部客户需求所需的车辆总数M。式（10）为需要的车辆数即划分的区域数量。

随机选取配送范围内M 个坐标点作为M 个区域的中心点，对于每个客户，计算其与各个中心点的距离，选择与其距离最近的中心点且该区域内的配送总量满足车辆容量约束时加入该区域内，若不满足则将其加入到距离次近的区域内，直至所有客户节点都加入到某个区域中。

计算每个区域的重心μj，并将重心作为新的区域中心重新划分客户，重复迭代上述划分的过程，算法的终止条件为达到区域内平方和最小化：

2.2 混合变邻域搜索算法

通过第一阶段的区域划分聚类算法将配送范围划分成M 个区域，从而将求解大规模问题转化为求解多个小规模的子问题，分别对每个区域的物流配送服务使用混合变邻域搜索算法（HVNS）求解。HVNS 可以被描述为，设s 为一个可行解，Nk（s） 是关于s 的一个邻域结构的解集，其中：k=1,…,kmax。HVNS 算法通过变邻域下降法（VND）拓展局部搜索，并混合模拟退火接受准则判断是否接受新解。混合变邻域算法的组成包括初始化参数、一组邻域结构、模拟退火接受准则和算法终止条件。

初始化参数包括初始可行解、初始温度、退火速率和最终温度，本文使用贪婪算法生成初始解。

邻域Nk-1（s）的局部最优s 优于Nk（s）的局部最优s'时以概率）接受新解，使得变邻域算法以一定概率进入下一个邻域，避免只在前几个邻域中搜索，扩大算法的搜索范围。

HVNS 的关键步骤是使用合适的邻域搜索方案，邻域结构的选择与邻域搜索方案的顺序都影响着HVNS 性能。本文采用了五种（lmax=5）邻域结构方案，包括插入法，2-opt，3-opt，cross-exchange 和大邻域搜索。插入法从路径中删除一个节点，并将其插入到路径的其他位置上得到一条新的路径，选择使得目标函数最小的插入方案；two-opt 将路径中的一段进行反转操作得到一条新的路径，若目标函数减小即进行反转，否则不反转；three-opt 首先删除路径中3 条边，生成3 条子路径，从而产生了7 种不同的重连方式，并找出其中最优的重连方法；cross-exchange 随机选取路径中两条子路径，且两条子路径没有重复的节点，交换两条子路径的访问顺序，生成新的路径；大邻域搜索包括destroy 和repair 两个算子。本文采用贪婪的思想设计摧毁和修复算子，计算摧毁节点后的节约值，将路径中对目标函数影响最大的节点摧毁。修复算子将被摧毁的节点插入到路径中对目标函数影响最小的位置。

变邻域下降（VND）是HVNS 最关键的部分，VND 的原理基于一个事实：一个邻域结构的局部最小值对于另一个邻域结构未必如此。VND 拓展了局部搜索，当在一个邻域结构内陷入局部最优时跳出该邻域结构重新寻找另一邻域结构内的局部最优，全局最优是关于所有可能的邻域结构的局部最优。

在遍历一个邻域后，通过退火速率更新当前温度，算法终止条件为温度达到设定的最终温度。

表2 给出了两阶段算法RPCHVNS 的伪代码。

表2 两阶段算法的伪代码

3 算法实验与结果分析

针对提出的两阶段策略，本文通过随机生成的方法生成数据进行数值实验。通过多组实验对比，得出本文算法在求解较大规模的同时取送货问题时优于其他同类算法。

3.1 算例构建与有效性验证

本文采用随机生成的方法构建算例，构建一个大小为30km×30km 的欧氏平面，配送中心的坐标为（15,15），客户规模为200个，客户的配送需求满足均值为5，标准差为2 的高斯分布，设定25%的节点有取货要求，5%既有送货也有取货需求的客户节点，详细的客户信息见表3。设定运输车的载荷为150kg，车辆的固定启动成本c1为600 元，车辆平均行驶速度为50km/h，单位距离的行驶成本c2为5 元，运输车从配送中心出发，完成规划的配送任务后返回配送中心。算法使用Python3.8 编程，在主频2.1GHz，8GB 内存的PC 上运行。

表3 配送信息

算法第一阶段RPC 算法是将问题按规模划分为多个子问题，使得每个子问题的规模为一辆运输车即可完成全部服务，计算总送货量为755kg，总取货量为290kg，通过式（10）计算得出M 值为6。通过区域划分聚类算法对所有点进行划分，聚类的结果如图2 所示。

图2 客户节点聚类结果图

通过第一阶段的分解后，使用HVNS 分别求解子问题，设置初始温度为50 000，退火速率为0.98，最终温度为15，返回迭代过程中出现的最优解。算法求得6 条配送子路径。使用两阶段算法生成的配送方案路线图如图3 所示，每一个闭环代表一辆运输车的配送路径。

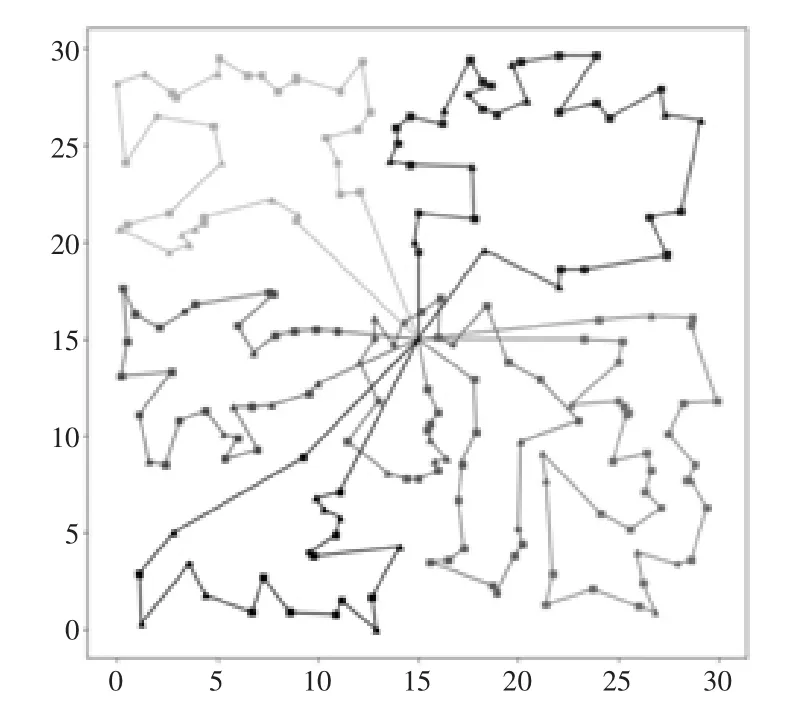
图3 配送方案路径

生成的配送子路径中，路径中服务的客户数量有的区别较大，但配送的里程接近，如路径6 的客户服务数量为21，配送里程为62.3，路径3 的客户服务数量为40，配送里程为68.1，与路径6 的里程接近，在平均速度近似的情况下，每辆运输车的配送时间也接近。由于RPC 算法仅有地理坐标与车辆载荷维度的约束，因此若考虑到配送中的装卸货的需求，会有任务分配不均匀的情况发生。

3.2 算法对比与分析

针对3.1 构建的算例，本文对比了文献[9]中提出的变邻域搜索算法（GVNS）和文献[20]中提出的的改进遗传算法（GA）。分别使用各算法求解10 次，得到计算结果的平均值与标准差，算法对比结果如表4 所示。结果显示，本文所提出的两阶段策略在处理较大规模的算例上具有优势，对比文献[9]的GVNS，车辆行驶距离减少了17.8%，成本节约了8.6%，时间节省了77.9%；对比文献[20]的GA，车辆行驶距离减少了82.8%，成本节约了66.6%，时间节省了73.8%。两阶段算法在规模较大时解的质量与求解时间均优于传统启发式算法，这是由于当算例规模增大时，解空间呈指数级增长，传统启发式算法每次迭代都需要花较长时间，难以收敛，两阶段的策略将大规模问题划分为多个小规模的子问题，减少了计算时间，同时提高了算法的寻优效果。

表4 与算法结果对比

3.3 构建多个规模算例

本文将RPCHVNS 算法应用于几个不同规模的算例，并与GVNS 和GA 的计算结果进行对比分析。构建客户规模分别为20、50、100 和200 的随机算例，算例的构建方法与3.1 中采取的方法相同。分别对每个规模求解10 次，获得其配送成本的最优解、平均值与标准差。不同算法在不同规模算例下的数值结果如表5 所示。

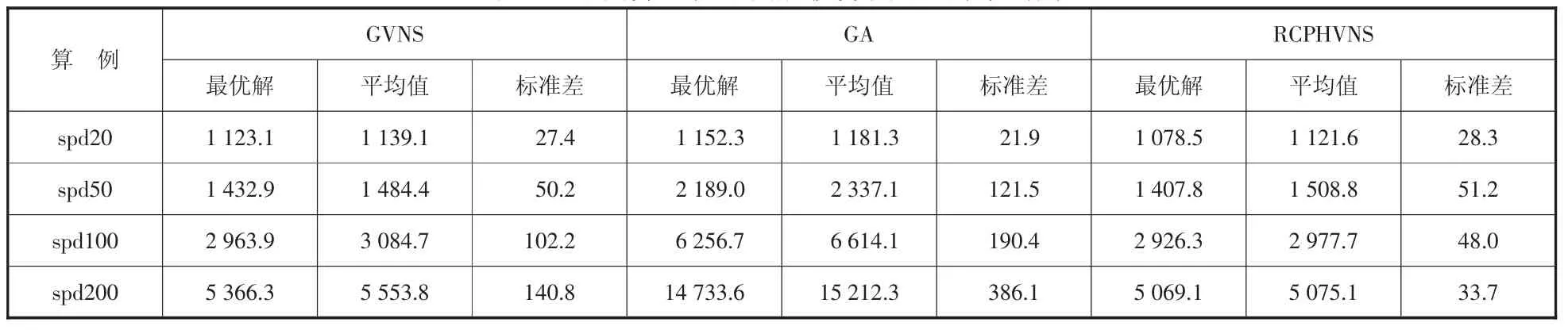
表5 不同算法在不同规模算例下的数值结果

计算结果显示本文提出的RPCHVNS 算法在求解不同规模问题上都有良好的性能表现。在客户规模为20 的算例中，RPCHVNS 与GA 和GVNS 的效果区别并不明显，从标准差上看，GA 与GVNS 能够得出比本文算法更加稳定的结果；当规模达到50 时，由于GA 的局部搜索性能较差，求解质量较差，GVNS 和RPCHVNS 的表现良好；当规模超过100 时，可以看出RPCHVNS 能够得出的解更加优秀，且稳定性表现良好。因此，本文提出的RPCHVNS 更加适合规模较大的问题，解的质量和稳定性都表现良好。

4 结论与展望

本文考虑了实际物流配送中常见的同时取送货的情景，构建了带同时取送货的物流配送数学模型，采用了两阶段算法RPCHVNS 求解该类问题，首先通过区域划分聚类算法将问题分解为多个小规模的子问题，对于每个子问题，设计了混合变邻域搜索算法求解配送路径。通过数值实验证明了RPCHVNS 在求解不同规模同时取送货物流配送问题的有效性，对比传统启发式算法，RPCHVNS 在客户规模较小时优越性并不明显，当规模增大到数百个时，本文算法在求解时间和数值结果上都有良好的表现，这为企业在开展同时取送货业务时提供了参考意义。

本文在第一阶段的聚类过程中，仅考虑了地理位置与车辆载荷约束，而实际配送过程中可能会有装卸货与时间窗约束，而当约束增多时，不可行解的数量也增多，算法的寻优能力难以保证。因此下一步的工作将对考虑时间窗和装卸货的同时取送货问题展开研究，并不断改进RPCHVNS 的寻优性能。