基于改进新型电压模型的永磁同步电机控制*
2023-02-04邹积浩翁如杰
陈 雄,邹积浩,任 佳,钱 鹏,翁如杰
(1.浙江理工大学机械与自动控制学院,杭州 310018;2.浙江大学计算机科学与技术学院,杭州 310058)
0 引言
永磁同步电机具有众多优点,为了提高PMSM的性能,研究人员将直接转矩控制(DTC)方法应用到PMSM中。传统转矩控制的缺点是会引起大的扭矩和磁链波动,国内外的学者将减小脉动问题视为主要研究对象,林海啸等[1]改变逆变器为了获取更多的电压矢量,结果表明对转矩脉动有很好的抑制效果,但是使控制模型变得更加复杂。近些年有学者提出的空间矢量调制(SVPWM)的直接转矩控制法(SVM-DTC),目前SVM-DTC算法[2-4]实现有PI调节法,PI调节法是利用观测的磁链和转矩与理想值的差值经过PI调节器,生成参考电压,ACHALHI、秦玉贵等[5-6]尝试使用模糊控制来改善脉动,实验表明这些控制方法产生了良好的效果。
定子磁链观测器是转矩控制的核心要素,传统电压模型磁链观测器使用纯积分器来估计定子磁链[7-8],由于感应电动势中有直流量影响,且直流量经过纯积分器会产生累积。故去除直流量是磁链观测器的重要内容。有学者提出采用滤波算法改善直流量累计的问题。WU等[9]提出自适应磁通补偿的磁链观测器,通过PI调节器消除直流偏置。还有一些采用了串联高通滤波器[10-12]的方法,这种方法可以有效地抑制住直流量累计,但是并没有去除定子磁链中存在的直流量,WANG等[13]将5个低通滤波器和1个高通滤波器串联解决了直流量问题,但实现磁链观测过程比较复杂。
本文选用SVM-DTC为研究模型,保证系统的磁链和转矩没有产生大脉动,同时为了提高PMSM驱动器效率,采用最大转矩电流比(MTPA)控制方法作为参考磁链给定方式,其特点是合理配置d-q轴定子电流,以最小的定子电流产生期望转矩,通过这种策略,可以降低铜损,并且实现对参考磁链的动态调整,而定子磁链观测是用一种改进新型电压模型获取,改进新型电压模型采用2个离散滤波器相互结合的方式,并对输出结果进行幅值相位的补偿,并改变磁链观测器的内部结构,这类方法不仅过程简单,还能够有效去除电压电流中包含的直流量,并提高系统的动态性能,保证观测磁链的稳定。
1 SVM-DTC原理分析
1.1 电机数学模型
永磁同步电机在静止坐标系下的电压方程为:
(1)
电压模型获取定子磁链表达式为:
(2)
电流模型获取定子磁链表达式为:
(3)
定子磁链大小和角度为:
(4)
电磁转矩与磁链和电流的关系为:
(5)
式中,Rs为定子电阻;Us、is、ψs为定子电压、定子电流、定子磁链空间矢量;Uα、Uβ、iα、iβ、id、iq、ψsα、ψsβ、ψd、ψq为定子电压、定子电流、定子磁链分别在α、β轴和d、q的分量;ψf为永磁体磁链;θs为定子磁链角度;Lq、Ld为交直轴电感;Te为电磁转矩;p为电机极对数。
1.2 SVM-DTC原理
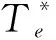
(6)
式中,Ts为采样时间。将生成的α、β轴的电压矢量输入进SVPWM模块产生脉冲信号驱动电机,可以有效减少磁链和转矩的脉动。
2 参考磁链生成原理
电机在运行过程中当负载变化时,会引起转矩和磁链变化,给定参考恒定磁链幅值会影响电机的效率,产生过多励磁损耗,而给定变化参考磁链幅值不仅可以提高系统的功率因数,也能够控制定子电流为极小值时输出最大转矩。
将式(5)转换到d-q坐标轴上得到公式为:
(7)
对式(7)求导为0可得电磁转矩Te和d轴电流id与q轴电流iq的关系式:
(8)
(9)
此时就推导出电磁转矩Te和q轴电流iq的关系式,取iq为-7 A~7 A(选用电机额定电流为7 A),最后利用polyfit函数求出电磁转矩Te和iq的关系式:
iq=0.3877Te
(10)
再利用求出iq带入式(8)中得出id,最后将id和iq带入式(3)、式(4)中求出给定参考磁链幅值。
图1是转矩和定子电流关系图,从图中可知随着电流增大,Te的幅值是变大的。

图1 转矩和电流关系
3 电压型磁链观测模型
3.1 传统电压模型原理
传统定子磁链求法是使用纯积分去获得,这种方法计算量小,也不需要应用太多电机参数,但是这种方法也存在很多问题,例如会引起直流量累计导致系统不稳定。
以β轴为例,将式(2)离散化可得式(11):
ψsβ(n)=ψsβ(n-1)+[Uβ(n)-iβ(n)Rs]Ts=ψsβ0+
(11)
式中,ψsα0为初始磁链值;Uβ(j)、iβ(j)、Eβ(j)分别为j(j=1……n)时刻β轴的电压、电流、感应电动势的值。当感应电动势会发生幅值为C的偏移,磁链值就会变成式(12)。
(12)
由此可见,若感应电动势产生幅值偏移,偏移量经过纯积分型磁链观测器会导致直流量累加,从而使磁链值发生畸变。
3.2 低通滤波法原理
为解决传统电压模型出现的问题,文献[11]采用低通滤波法(LPF)去解决,LPF法获取磁链原理:
(13)
式中,wc为截止频率;Es为感应电动势矢量。以β轴为例,离散化式(13)可得:
(14)
继续给感应电动势施加直流量C,则经过LPF的感应电动势产生的磁链为:
(15)
可以看出,LPF法对直流量C有抑制作用,直流量C的值变成了CTs/(wcTs+1),它抑制直流量能力与截止频率大小有关。
3.3 改进新型电压模型原理
针对前两种电压模型无法解决的问题,本文采用一种新型电压模型(new voltage model,Nvm),可以有效的去除直流量带来的影响。基本思路是采用2个滤波器进行并联构成1个新的磁链观测器:
(16)

将表达式(16)离散化可得:
(17)
(18)
(19)
(20)
若给感应电动势施加直流量C,以β轴为例,磁链表达式会变为:
ψsβ(k)=a(Eβ(k)+C-(Eβ(k-1)+C))+
bψsβ(k-1)-dψsβ(k-2)=
a(Eβ(k)-Eβ(k-1))+
bψsβ(k-1)-dψsβ(k-2)
(21)
可以看出,直流量被去除,说明新型电压模型观测器可以有效去除感应电动势中的直流量。滤波后虽然去除了直流量,但是也使得生成的磁链幅值和相位均发生变化,故要进行补偿操作。
传统电压模型频域表达式为:
(22)
新型电压模型频域表达式:
(23)
结合式(22)、式(23)可得:
(24)
(25)
(26)
结合式(24)、式(26)可得:

(27)
同理可得:
(28)
为了解新型电压模型观测器性能,对补偿后的算法进行分析,式(17)为Nvm离散化表达式。假设输入信号的频率为we1,在第t时刻,信号频率突变为we2,当前时刻经过补偿后的磁链ψs(k)以及下一时刻的ψs(k+1)为式(29)、式(30):
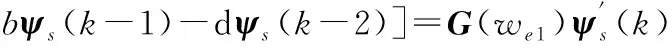
(29)

(30)
式中,G(we1)、G(we2)为幅相补偿矢量函数。
从式(29)、式(30)可以看出,当频率在t时刻发生突变时,此时幅相补偿函数也会发生突变,所以,在对输出磁链进行幅相补偿时会引起输出磁链发生突变,导致这一时刻输出磁链信号无法跟随理想磁链的问题。通过改变新型电压模型与幅相补偿环节的位置,即可提高系统整体的动态性能。改变后磁链观测器下一时刻的输出ψs1(k+1)为:

(31)

交换前:
(32)
交换后:
(33)
(34)

新型电压模型和幅相补偿环节交换后的框图如图2所示,将交换后的观测器定义为改进新型电压模型(modified new voltage model,MNvm)。

图2 改进新型电压模型
4 假定信号分析
利用MATLAB/Simulink对所提出的电压模型算法的性能进行了研究。假设当滤波器或积分器投入运行时,电机已在稳态下运行。为了便于分析,调整电动势的大小,通过比较仿真结果来验证。
假设输入感应电动势为:
(35)
式中,A=215 V;we=120π rad/s;t=0 s时C=0,现假设在0.5 s后C=3;采样时间Ts=1e-5 s,新型电压模型的截止频率为wc1=33π rad/s,wc2=5π rad/s,低通滤波法(lowpass filter,LPF)的截止频率为wc=36π rad/s。
图3为3种方法和理想磁链在β轴的磁链仿真比较图,当感应电动势存在直流量时,从图3中可以看出直流量经过纯积分器后会随着时间变化而增大,这样会引起直流量累积,验证了式(12)的结论。式(15)中LPF将直流量变成CTs/(wcTs+1),直流量得到了抑制,但是直流量依旧存在于系统当中,图3波形验证了这一结论。从式(21)中可以看出改进新型电压模型观测器可以完全消除直流量的干扰,并且图3中也能够看出没有产生直流偏移,并且加了补偿环节后的磁链幅值和相位与理想磁链十分接近。

图3 定子磁链在β轴分量
假设t=0.5 s后A=430 V,直流量C=0,电角速度we=240π rad/s,截止频率参数同上。图4为Nvm和MNvm前后对比图,从仿真结果中能够看出当输入感应电动势发生突变后,采用MNvm观测器生成的磁链平滑过渡,没有受到太大影响,而采用Nvm观测器出现较大误差,在t=0.5 s时磁链偏离实际值0.1 Wb,产生较大波动,在经过0.01 s后达到稳定。

图4 Nvm与MNvm输出磁链波形对比
5 系统仿真
在SVM-DTC系统中采用MTPA法给定参考磁链提高了电机的效率,使用改进新型电压模型取代传统电压模型,提高系统的抗干扰能力,并且保证系统的稳定性。图5展示了整个模型的系统框图,电机参数如表1所示,系统采样周期为1e-4 s。并在Simulink里面构建整个实验模型。
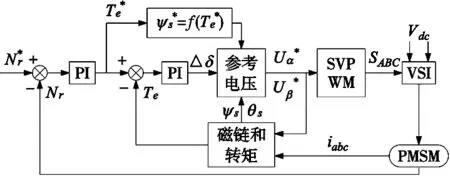
图5 系统框图
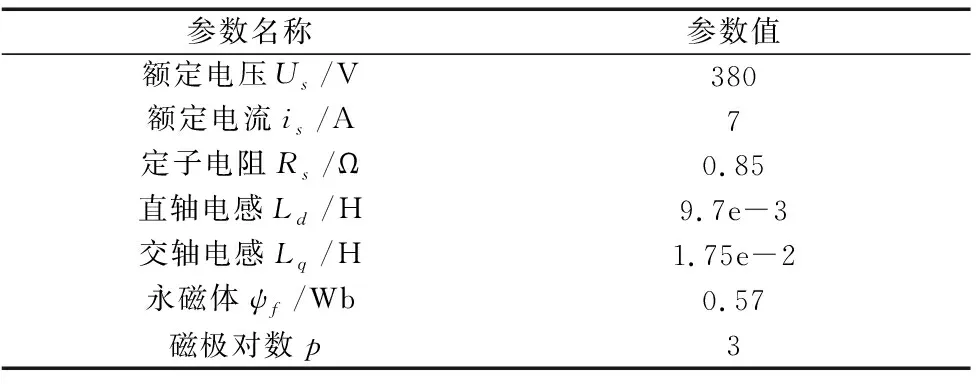
表1 电机参数
5.1 直流量测试


(a) 定子磁链α轴分量

(b) 定子磁链β轴分量
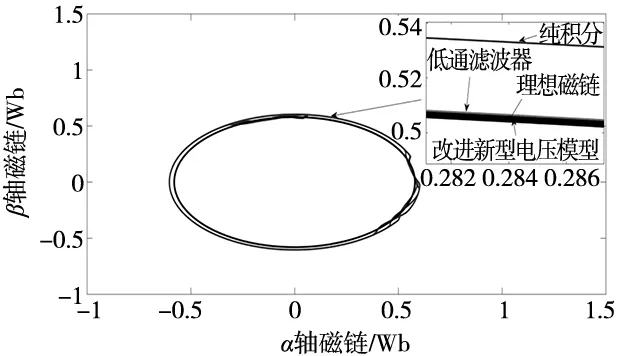
(c) 定子磁链圆图6 3类磁链观测器生成定子磁链波形比较
图7为3种算法下生成的速度波形对比图,图7a中由于直流量不断累计,导致速度波形逐渐发散,从图7b中能够看出LPF并未完全去除掉直流量,这导致电机运行过程中速度波形一直存在10 r/min的波动;图7c中速度波形稳定,当系统稳定时没有产生波动,仿真结果表明了MNvm对直流量具有良好的过滤效果。
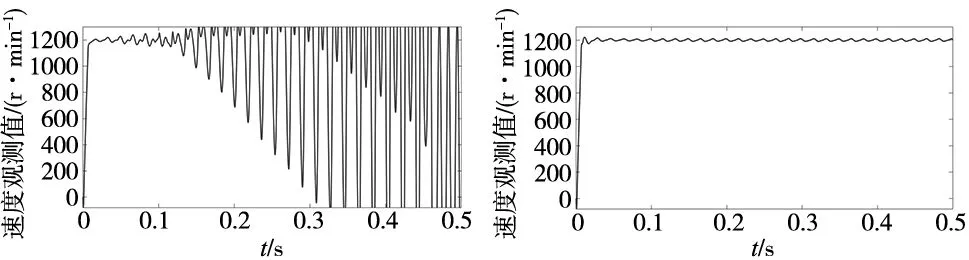
(a) 纯积分 (b) LPF

(c) MNvm图7 3类磁链观测器生成转速波形对比
5.2 给定磁链分析
图8为给定恒定参考磁链和变化参考磁链下负载转矩、α轴电流、定子磁链幅值观测值的波形图,其中恒定参考磁链值为0.6 Wb,系统启动时给定参考转速为1200 r/min,启动时带负载20 N·M,在0.5 s后负载转矩变成22 N·M;分析图8可以看出当采用恒定参考磁链方法时,在负载变化前,电磁转矩观测值约为19.5 N·M,α轴电流约为8.15 A,负载发生突变之后电磁转矩观测值约为21.5 N·M,电流变成8.85 A。当系统采用变化参考磁链方法时,在负载变化前,电磁转矩观测值约为20 N·M,α轴电流为7.8 A,负载发生突变之后电磁转矩观测值约为22 N·M,电流变成8.5 A,电磁转矩观测值大于恒定参考磁链系统生成的电磁转矩值,转矩值更加接近于负载转矩值,且电流值也小于前者,当负载值发生变化,参考磁链值会进行自我调整,使得系统以最小电流输出最大转矩,保证电机运行效率。
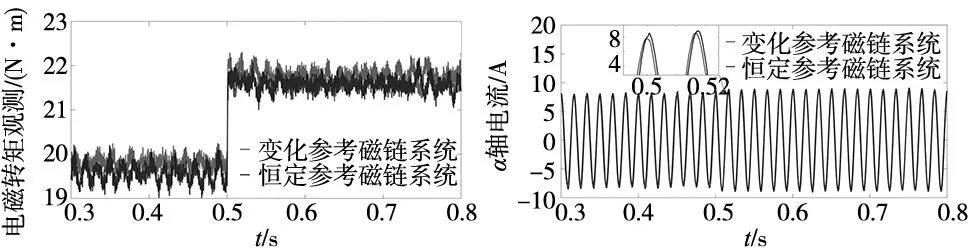
(a) 电磁转矩 (b) α轴电流
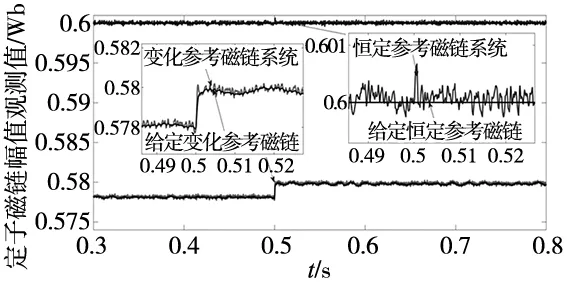
(c) 定子磁链幅值观测值图8 基于恒定参考磁链系统和变化参考磁链系统仿真
5.3 Nvm和MNvm动态性能分析
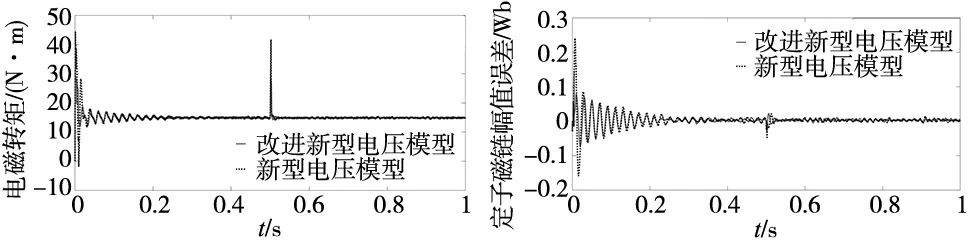
(a) 电磁转矩 (b) 定子磁链幅值误差

(c) 转速图9 基于Nvm系统和MNvm系统仿真
6 结论
为了更好的实现直接转矩控制系统的功能,本文采用了一种改进新型电压模型,该算法采用离散滤波器结合的方式来估算定子磁链,并对估算值进行幅值和相位补偿;考虑到传统给定恒定磁链方式导致电机运行效率偏低,为了提高电机效率,采用MTPA法去给定变化参考磁链值;最后本文将两种算法应用到SVM-DTC模型中,并得出如下结论:
(1)本文采用的改进新型电压模型解决了传统磁链观测器因直流量引起发散的问题,并对其进行离散化分析,找到一种消除直流量并改善动态性能的方式。仿真结果也体现出系统能够迅速应对速度变化的情况,并保持运行稳定。
(2)根据MTPA法给定变化参考磁链,当负载突变引起转速变换时,MTPA法能够对给定参考磁链进行调整,使得系统得到最优的转矩响应。通过与采用恒定磁链的系统进行仿真对比,采用MTPA系统产生电流更小。
