基于模糊控制蚁群算法的移动机器人路径规划*

刘建娟，刘忠璞，张会娟，袁 航，姬淼鑫

(河南工业大学a.电气工程学院；b.机电设备及测控技术研究所，郑州 450000)

0 引言

在科技进步和工业发展的推动下，以AGV为代表的移动机器人已经广泛运用到各类行业的技术革新和发展之中。如医疗行业的特殊服务机器人、智慧城市建设中AGV的设计和使用[1]。

路径规划是AGV技术中的重点和难点，保证AGV获得一条安全、节能、无碰撞的最优路径，完成相应的作业任务。在国内外的研究中，AGV路径规划算法种类众多[2]，包括Dijkstra算法、A*算法、人工势场法、遗传(GA)算法、粒子群(PSO)算法[3]、快速探索随机树(RRT)算法[4]以及蚁群(ACO)算法等。不同种类的算法优劣各不相同，如A*算法搜索速度快但寻优路径并不是全局最优[5]；遗传算法(GA)具有较强的鲁棒性，但是算法复杂，规划效率不高，并且存在寻优早熟现象[6]。其中，蚁群算法简单并且具备良好的全局搜索能力，在目前的路径规划研究和工程应用中是常用算法。

蚁群算法(ant colony algorithm)是一种具有正反馈和启发式搜索特性的生物启发式算法[7]。传统的蚁群搜索算法存在收敛速度慢、效率低等问题。国内外学者对此进行相应改进，LIANG等[8]提出一种结合遗传算法和蚁群算法的融合算法，解决蚁群算法容易出现早熟的现象，提高了蚁群算法的有效性和鲁棒性，但算法存在迭代速度缓慢，存在冗余节点的问题；AJEIL等[9]提出了一种蚂蚁种群迭代优化机制。该机制提出老龄化蚂蚁群的概念，并根据老龄化蚂蚁的数量和迭代结果计算和更新路径权重，以提高ACO算法的全局收敛性和稳定性。但该机制容易造成蚁群搜索多样性大幅降低，增加算法陷入局部最优的可能性。姚晓通等[10]引入带权重的节点概率搜索公式，并通过自定义信息素挥发因子更新机制进一步增加蚁群算法有向性引导和搜索能力，但在该机制的作用下，蚁群定向搜索能力加强，破坏全局多样性搜索和比较的平衡能力，在复杂环境中缺陷性较大。ZHENG等[11]提出一种“奖惩”策略，用于改进信息素更新效果，在一定程度上促进蚁群搜索收敛速度，但对于复杂障碍环境，蚁群搜索存在高度冗余性，“奖惩”策略的使用存在一定的局限，不利于全类型场景使用。杜力等[12]提出一种融合萤火虫算法的复合蚁群算法，通过萤火虫算法进行蚁群算法参数优化，通过精英策略促进全局极值搜索和收敛，但该方法减弱了蚁群算法的全局随机程度，存在收敛陷入局部极值的问题。

常规的蚁群算法在路径规划中存在路径最优性低、算法收敛速度缓慢等问题。为解决上述问题，本文在保证蚁群算法多样性搜索的基础上提出一种改进的智能自适应蚁群算法。本文改进蚁群算法，融合模糊控制技术，引入新的信息素更新策略，优化信息素更新效果。同时，改进节点搜索概率公式，动态调整蚁群算法节点概率搜索公式的计算因子，加快算法的收敛速度。此外，本文提出基于几何优化的路径节点优化算法，优化最短路径，减少冗余节点，动态更新最优路径。本文提出的改进蚁群算法，能够进一步减短最优路径长度，加快算法迭代收敛次数，避免算法陷入在局部最优，保证多样性。

1 环境建模与蚁群算法

1.1 环境建模

实际环境地图是AGV路径规划的主要应用场景。为了与路径规划算法相结合，环境地图常常使用栅格地图[13]建模的方式展现，如图1所示。其中黑色阴影区域为栅格地图中的障碍物标识区域，空白区域为AGV允许运行区域。

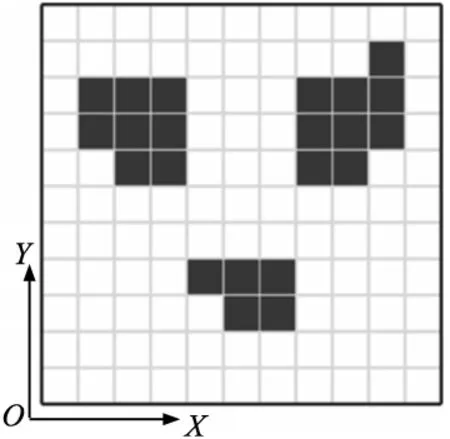
图1 二维栅格地图建模

假设实际环境地图为正方形地图，栅格化建模后，以栅格地图的左下角为坐标系原点建立OXY坐标系，每个栅格的长度为一个单位a，栅格地图每一行共有M个栅格，那么栅格地图的栅格数总量为M*M个。设当前AGV所在栅格为第G个栅格，那么此时AGV所在位置的二维坐标(x,y)可由式(1)和式(2)计算。

(1)

(2)

式中，mod为取余符号；ceil为向上舍入的取整符号。

此外，实际环境地图存在不全为正方形的特殊情况。对于此，栅格化建模通常采用“地图规则化”处理，即扩大栅格化地图范围，其中扩大的栅格范围设定为AGV不可行区域的处理方式，如图2所示。其中，图2a为实际地图俯视图，阴影区域为障碍物，图2b为栅格化建模地图，条状阴影区域为扩大范围的地图障碍物区域。

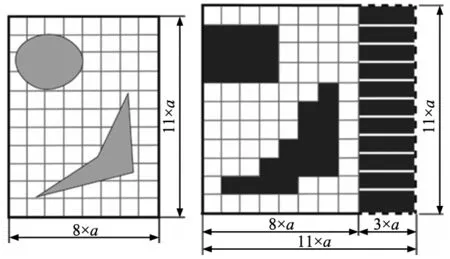
(a) 实际地图俯视图 (b) 栅格化建模地图图2 特殊环境建模

实际环境地图根据上述建模规则进行二维栅格化处理，使用栅格坐标标记AGV位置等参数，并支撑路径规划算法的运行和实现。

1.2 路径规划基本蚁群算法

蚁群算法是以自然界蚂蚁寻找食物的自然现象为主要思想进行设计算法[15]，能够良好地解决优化控制领域、路由分配及路径规划等问题。

路径规划技术中的蚁群算法实现主要包括算法初始化、转轮赌法寻找下一合适节点和信息素更新3部分。其中，蚁群算法初始化主要进行蚁群参数设定，包括：蚁群算法起始点和目的点、蚂蚁种群数量、信息素初始分布、迭代次数的设置以及信息素蒸发率的设定等，其中，蚁群寻路起始点和目的点即为机器人路径规划的起始点和目的点。在寻路迭代次数为t时，蚂蚁z从节点i转移到节点j的概率如式(3)所示。

(3)

(4)

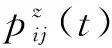
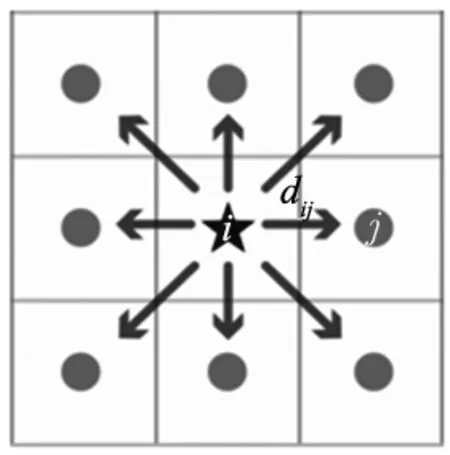
图3 蚁群搜索八向示意图

每只蚂蚁重复上述寻路过程，直至通过概率公式计算确定下一节点为路径规划目的点或迭代次数达到预设值时，完成一次寻路过程。当所有的蚂蚁完成一次寻路之后，每条路径节点上的信息素浓度开始进行更新，更新计算如式(5)所示。

(5)

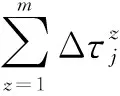
(6)

式中，Q为正常数，一般设定为1；Lz为本次寻路得到的最优路径的长度数值。

蚁群通过概率选择、信息素更新等步骤不断迭代循环，利用正反馈特性不断促进算法收敛，实现路径规划。

2 融合模糊控制的改进蚁群算法

本文提出一种路径规划中融合模糊控制的改进蚁群算法FOACO，解决蚁群算法在路径规划过程中存在的收敛速度缓慢、精确度有待提高等问题。改进蚁群算法提出3个策略优化方法：信息素更新策略改进、权重因子自适应调整和规划路径几何优化。

2.1 初始化信息素浓度分布规则

普通蚁群算法路径规划信息素初始分布为均一分布，全局信息素无差排列，蚁群寻路过程出现盲目性和不确定性，影响全局性能。为了增大初始化信息素的启发作用，本文引入一个初始化信息素浓度分布规则，如图4所示。

图4 初始化信息素分布

根据规划起点和终点建立信息素浓度特殊初始化区域，其余区域为信息素普通初始化区域。信息素初始化分布如式(7)所示。

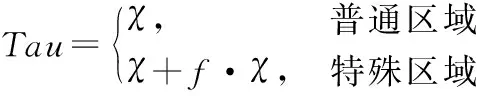
(7)

式中，χ为普通信息素初始化浓度分布数值；f为特殊分布系统，取值范围为[0,0.5]。通过增加信息素初始分布，构建蚁群有向性移动最优路径区域，降低蚂蚁寻路的盲目性和不确定性，加快蚁群算法路径规划速度。

2.2 融合模糊控制的信息素更新策略改进

普通蚁群算法信息素更新启发性较弱，全局规划精度和速度不足。本文引入二维模糊控制器进行蚁群经过路径节点信息素更新增量的计算与控制。模糊控制器输入变量为蚂蚁所在节点信息素浓度值Tau和当前时刻传统信息素更新策略的信息素更新值ΔTau_tra，模糊控制器输出量ΔTau_Fuzzy作为信息素更新的变化量之一。模糊控制器结构如图5所示。

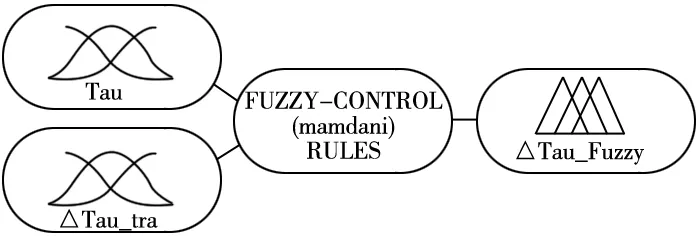
图5 模糊控制器设计

模糊控制器的变量隶属度函数根据专家经验知识选定。其中，三角型隶属度函数和广义钟型隶属度函数对于离散系统具备良好的计算能力和平滑处理能力，因此，本文模糊控制器的隶属度函数设计如表1所示。

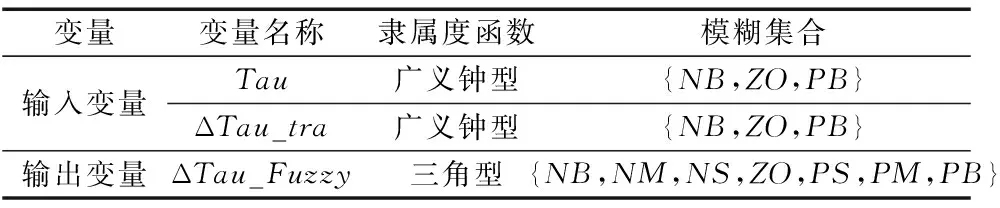
表1 模糊控制器的变量模糊化

同时，模糊控制器输出量的论域选定为[0.001,0.1]，为避免模糊控制器输入溢出影响算法速度，本文选用的输入和输出变量隶属度函数如图6所示。

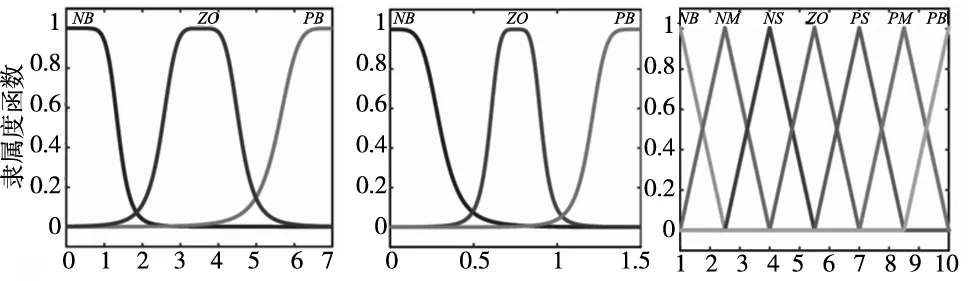
(a) Tau (b) ΔTau_tra (c) ΔTau_Fuzzy图6 隶属度函数

蚁群算法规划路径长度随着迭代次数的增加逐渐趋近于收敛状态。在路径规划趋近收敛状态中，普通信息素增加值的启发作用不明显，因此，蚁群算法路径规划速度受到极大的限制。为解决这个问题，本文引进收敛状态信息素增量ΔTau_ste计算方式为：

(8)

式中，lengthk为第k次迭代的路径长度；itermax为最大迭代次数；R为常数。综上所述，改进蚁群算法信息素更新策略为：

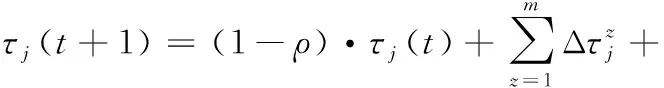
(9)

式中，ΔTau_Fuzzy(j)为模糊控制器输出量的值，即模糊控制器输出的节点j的数值增量。

2.3 蚁群参数自适应调整规则

普通蚁群算法参数数值固定，容易引起算法收敛速度降低，甚至不利于算法收敛。为了提高蚁群算法稳定性和快速性，本文采用信息素权重因子和蒸发率自适应调整规则，进行算法优化。信息素权重因子自适应调整为：

(10)

式中，lengthop为第k次迭代最优路径长度；R为常数。根据规划路径长度进行信息素启发因子数值调整，增大信息素在后续迭代规划中的启发性，促进算法快速收敛。同时，信息素蒸发率固定，随着迭代次数增加，路径节点信息素累积速度超过蒸发速度，容易出现冗余节点和冗余路径。现引入信息素蒸发速率自适应调整规则，提高路径节点蒸发速度。若第k次迭代路径长度大于第k-1次，为减小较差路径信息素浓度的启发作用，促使蚁群向更优路径移动，现对信息素蒸发率进一步增加，如式(11)所示：

(11)

通过信息素权重因子和蒸发率自适应调整，对全局迭代路径信息素浓度有向性处理，加快全局最优路径的规划速度。

2.4 规划路径几何优化算法(FOACO)

为了进一步优化改进算法FACO的性能和效果，采用几何原理进行路径优化，即利用三角形两边的长度之和大于第三边的特性去除路径中的冗余点。如图7所示，路径节点为1→2→3→4→5，以三个节点为一组判断冗余节点，D为极限距离，如式(12)所示，其中a为栅格边长。假定节点组为3，4，5，以首尾节点为固定两点建立直线y=K*x+B，计算中间节点距离该直线的距离d，并以此为节点冗余判断参数。假设数值d大于极限距离D，则直线y经过障碍物，节点4不可删除。反之，节点4为冗余节点，删除优化后，路径为1→2→3→5。

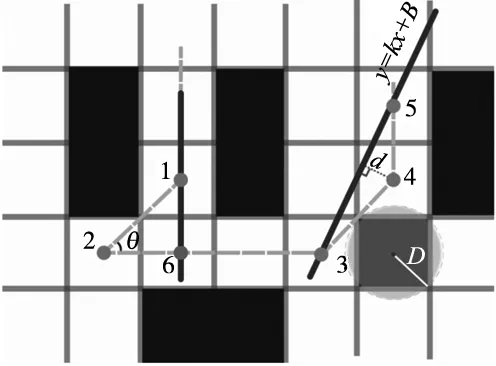
图7 几何优化示意图

(12)

结合路径规划结果中存在锐角路径转折的特殊情况，如图7中路径节点组1→2→3，采用上述冗余路径判断方法可能出现“几何优化”无效的问题。本文采用“检测锐角—增加节点优化”的处理方法，即增加节点6，更新路径节点组为1→2→6，重复进行冗余路径判断过程，如图7所示。几何优化后路径为1→6→3→5，与原路径相比，路径长度进一步缩短，优化路径规划整体效果。

2.5 FOACO算法总体流程

结合上述改进策略：信息素更新策略改进、权重因子自适应调整和规划路径几何优化，改进算法工作流程如图8所示，通过改进措施，动态更新蚁群算法参数数值，优化算法整体结构，额外增加几何优化步骤提高改进算法的完整度。

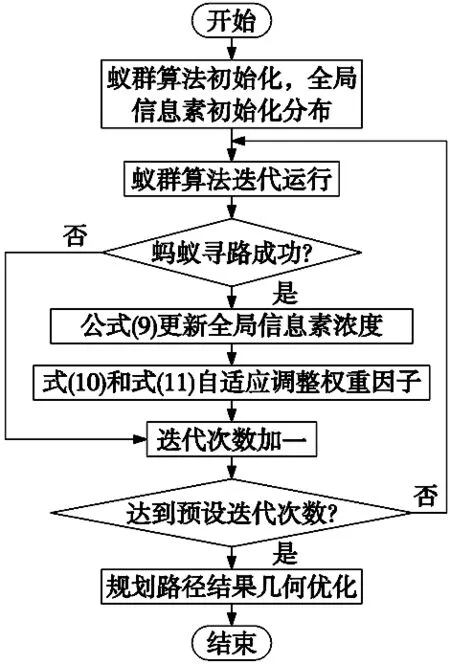
图8 改进蚁群算法(FOACO)流程图

3 仿真实验与验证

为了验证本文算法的可靠性，在MATLAB 2017a开发平台下编写算法，实验硬件设备为：Intel(R)Core(TM)i5-6200U CPU@2.40 GHz和8 GB运行内存。本文根据不同实验环境分别设置三组对照实验，采用普通蚁群算法ACO、遗传算法改进蚁群算法GACO和本文算法FACO进行算法效果对比，实验地图大小为20×20。此外，三组蚁群算法基础参数设置如表2所示。

表2 基础蚁群算法参数设置

本文设置两种仿真地图，分别为一般地图MAP1和文献[15]地图MAP2，对照实验结果如图9所示。

(a) MAP1 (b) 迭代曲线

(c) MAP2 (d) 迭代曲线图9 对照实验

如图9所示，通过本文改进方法实现，FACO算法规划路径收敛速度优于普通蚁群算法ACO和融合遗传算法的蚁群算法GACO，规划路径长度也有不同程度的降低改善。与文献[15]的改进蚁群算法相比，本文算法收敛性能和路径最优程度均进一步得到提升，规划路径转折次数降低，路径更加平滑。加入几何优化策略后改进蚁群算法FOACO路径规划结果如图10所示。

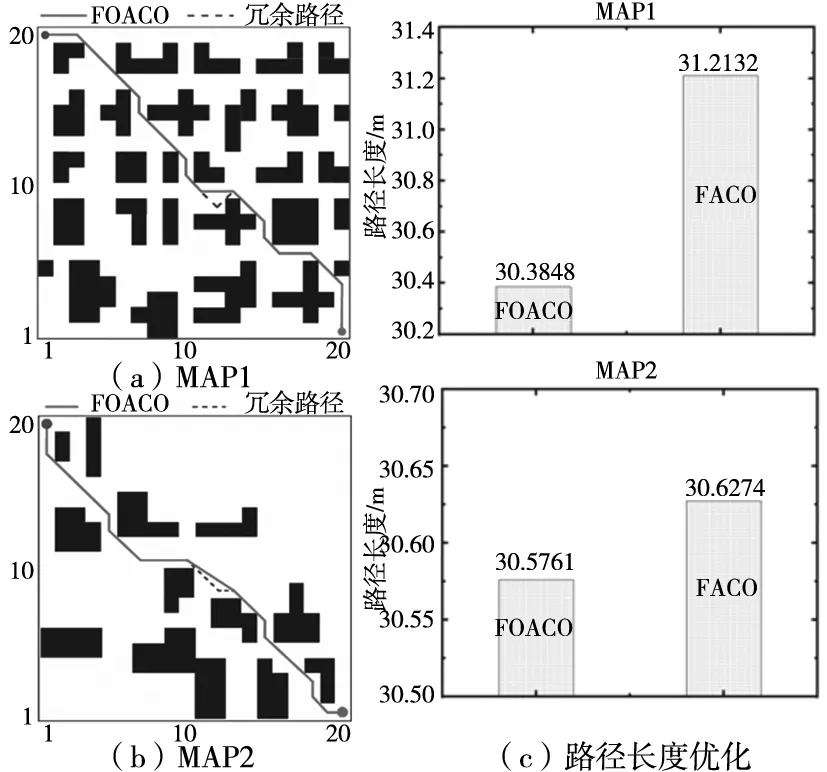
图10 FOACO几何优化实验

结合图10和表3，本文改进FOACO算法与对照组算法相比具有更强的最优路径规划能力。对于MAP1，本文算法与ACO和GACO相比，路径长度减小8.51%和6.17%，迭代次数减小27.9%和36.73%；对于MAP2，本文算法与文献[15]相比，路径长度减小0.371%，迭代次数减小6.25%。因此，本文改进蚁群算法具备一定的优越性。

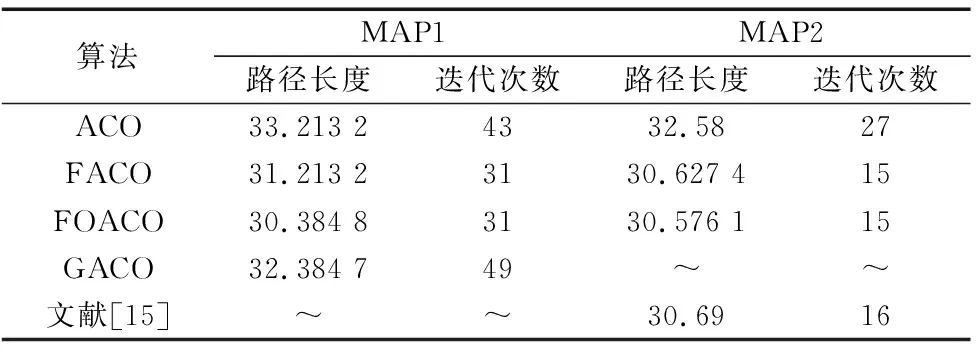
表3 仿真对比实验数据表

4 结论

本文提出一种融合模糊控制和自适应权重信息调整的改进蚁群算法来优化移动机器人路径规划技术的性能。首先使用信息素初始化规则提高初始信息素启发能力。同时，引入模糊控制和收敛状态信息素增量改进普通蚁群算法的信息素更新策略，进一步提高信息素更新效果，促进算法全局最优收敛；采用自适应权重因子调整的方式，促进蚁群算法快速迭代和收敛；最后，采用几何优化算法进一步优化规划路径，进一步缩减路径长度，深化全局收敛路径结果的最优性。实验表明，本文算法能够有效地提高移动机器人路径规划性能，缩减路径长度效果明显，有效减低最短路径迭代次数，整体效果优于其余同类型算法。结合移动机器人实际使用场景，下一步可着重于动态障碍物蚁群算法路径规划性能改进与提升的研究工作，尽可能拓宽本文算法应用场景和技术深度。