基于多传感器鲁棒容积卡尔曼融合的半潜式起重平台立柱快速压载舱液位估计
2023-02-04肖业方郭蕴华高海波
肖业方,郭蕴华,高海波,胡 义
(武汉理工大学a.高性能舰船技术教育部重点实验室;b.能源与动力工程学院,武汉 430063)
0 引 言
随着世界上油井和海工平台迎来新的报废高峰期,半潜式起重平台作为一种重要的海洋拆卸平台得到了快速发展[1]。半潜式起重平台的作业要求特殊,起吊过程中会产生巨大的倾覆力矩。为保持平台稳性,平台排水量会急剧增加数千吨,此时需要采用空气排载系统。空气排载系统利用高压空气将舱室内的液体吹除,其排载速度可达常规离心泵的数十倍[2-5]。同时,正因为空气排载系统的排载速度较快,其立柱快速压载舱液位估计的可靠性和稳定性对于半潜式起重平台的安全作业就极为重要。为此,可在立柱快速压载舱中配置多个液位传感器,并通过滤波算法和信息融合技术提高液位估计的可靠性和稳定性。
已经有学者对滤波算法进行了深入研究,先后提出了卡尔曼滤波(Kalman Filter,KF)、拓展卡尔曼滤波(Extended Kalman Filtering,EKF)[6]、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)[7]、容积卡尔曼滤波(Cubature Kalman Filters,CKF)[8]等方法。近年来,信息融合技术因为具有可扩展性、低通信量、对节点故障鲁棒性强等优点受到了越来越多的关注。Olfati-Saber等[9-11]针对离散线性高斯系统,利用平均一致性方法提出了分布式卡尔曼滤波(Distributed Kalman Filter,DKF);Li等[12]基于一致性理论采用统计线性误差传播的方法,通过引入伪观测矩阵提出了分布式UKF算法;丁家琳等[13]利用信息滤波和平均一致性理论提出一种分布式CKF 算法。近年来不少学者将这些技术用于液位测量系统中,丁雨淋等[14]以实时水位观测为对象,通过水文变化语义知识约束,实现了卡尔曼滤波(Kalman Filter,KF)参数的自适应调整,提高了水位测量的精度;刘经宇等[15]以锅炉的汽包水位测量为对象,将KF 算法用于单通道的汽包水位滤波,再将各通道滤波后的值进行求平均值方法融合,得到了更准确的汽包水位;刘庆华等[16]以船舶高精度液位测量为对象,将EKF 算法用于船舶液位测量中,并将多传感器滤波后的值进行加权融合,得到了更可靠的液位值。
美国“智能维护系统中心”研究表明:自动化系统40%以上的故障报警是由于传感器系统自身的故障而产生的误报[17]。传感器的自身故障会导致观测野值,进一步导致滤波估计的性能严重退化,并由错误的估计触发错误的报警,严重干扰系统的运行和人员的判断。为此,Huber 等[18]提出了广义极大似然估计(M 估计),降低了观测野值的权重。Tseng 等[19]将基于Huber 估计的CKF 滤波算法应用于GPS 导航系统。彭美康等[20]在CKF 算法中引入了基于平方根逼近函数的修正因子以抑制野值的影响。这些鲁棒估计方法对于含有较少野值的情形较为有效,一旦某一传感器因为机械故障或者接触不良处于半失效状态,会导致观测中存在高比例的野值。此时,已有融合算法的估计性能会严重退化,甚至出现融合估计反而不如单传感器估计的情况。并且,液位估计方程不存在线性统计误差传播问题,现有的非线性分布式融合算法不适用于液位估计系统。针对以上问题,本文提出了一种多传感器鲁棒容积卡尔曼融合算法(MSRCKF),并将其应用于半潜式起重平台立柱快速压载舱的液位估计中。在单一传感器半失效的情况下,即使含大量野值,系统通过MSRCKF算法仍可以得到稳定可靠的液位估计。
1 空气排载数学模型
1.1 状态方程
半潜起重平台立柱快速压载舱压缩空气排水过程分为两个步骤,第一步是舱内建压,此时海底阀的阀门外处压力大于内处压力而处于关闭状态,舱内开始充入高压气体;当海底阀的阀门内外处压力相等时进入第二步,此时海底阀打开,舱内持续充入高压气体,舱内液体在高压的作用下从海底阀排出。基于理想气体状态方程与伯努利方程对其进行分析,以舱室状态的真实变化建立系统的状态方程:

式中,xk为k时刻下系统的状态向量,f(xk-1)为k-1时刻的真实值对k时刻的预测,wk-1为k-1时刻系统的过程噪声,Γ为过程噪声分布矩阵。
xk是由舱内水质量(单位:t)、舱内空气体积(单位:m3)、舱内空气进入质量(单位:kg)、舱内气压(单位:Pa)、舱内外气压差所对应的水柱高度(单位:m)、舱内液位(单位:m)、海底阀阀门处水流速(单位:m∙s-1)和海底阀阀门处水体积流量(单位:m3∙s-1)构成的8维状态向量,即系统的状态向量维数n为8,xk可表示为
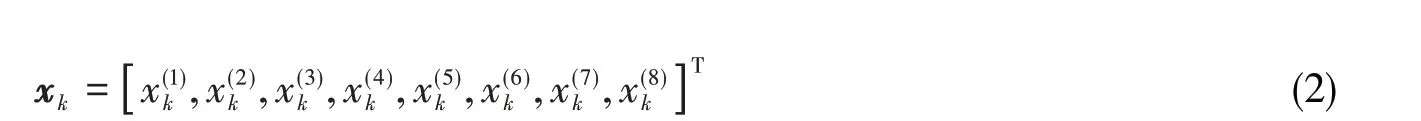
f(xk-1)的映射关系可用以下公式表示:

式中:Δt为时间步长,单位为s;ρwater为海水密度,单位为kg∙m-3;QAir为充入压缩气体的质量流量,单位为kg∙s-1;TAir为舱内气体的开尔文温度,单位为K;RAir为气体常数,单位为J∙(mol·K)-1;M为空气摩尔质量,单位为kg·mol-1;Ppri为舱内初始气压,单位为Pa;Patm为标准大气压,单位为Pa;g为重力加速度,单位为m∙s-2;fcap(⋅)为舱容表函数,由舱室的舱容表决定;H0为外界液位离舱底的距离,单位为m;kwater为海水阻力系数;S为海底阀的阀门总面积,单位为m2;Nwater为海底阀数量;r为海底阀阀门半径,单位为m。
1.2 量测方程
以液位传感器的测量建立系统的量测方程,即

式中,zk为k时刻下舱内液位传感器的测量值,H为量测转换矩阵,vk为k时刻系统的测量噪声。
vk与wk均为高斯白噪声且互不相关,它们的统计特性为

2 鲁棒CKF算法
2.1 CKF算法
CKF 算法的核心思想是通过球面径向容积准则进行相应的数值积分运算,是当前最接近贝叶斯滤波的近似算法,主要有时间更新和量测更新两个步骤。假设已知系统在k-1 时刻的后验密度函数为p(xk-1|zk-1)=N(x̂k-1|k-1,Pk-1|k-1),CKF算法计算流程如下:
Step1——时间更新
对协方差矩阵Pk-1|k-1进行Cholesky分解得到Sk-1|k-1,即
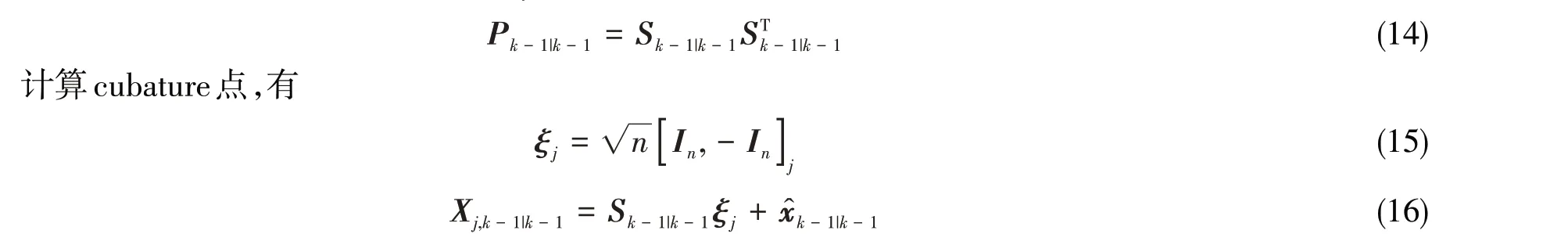
式中,ξj为第j个容积点,j=1,2,…,2n,n为系统的状态向量维数,In为n维单位矩阵,[⋅]j表示矩阵[⋅]的第j列。
通过非线性状态函数对cubature点进行外推预测,有

2.2 Huber-CKF算法
Huber-CKF 算法与标准CKF 算法的区别主要在于引入了Huber 等价权函数,将滤波增益K中的Rk重构为

式中,Ψz=diag[ψ(ei)]为稳健因子,ψ(ei)为等价权函数,即

式中,ei为(zk-ẑk k-1)(加权观测残差)的第i个分量,β为阈值。
2.3 鲁棒CKF算法
对线性量测方程构建线性回归模型,即

式中,χk=yk-gkxk,为标准化残差。且函数ρ(χk)的表达式为

事实上,因为真值xk不可知,在计算中用外推预测值x̂k|k-1代替真值,故式(41)中δxk|k-1的值为0。同时,式(41)中的vk也可以视为观测残差,即vk=zk-ẑk|k-1。为了与观测残差的经典表示方法一致,令ek=vk,有

观察式(42)可知,Φk是一个基于观测残差的无量纲数。构建矩阵Ω为

式中,m为观测向量维数。
根据矩阵Ω对误差协方差矩阵进行重构,有

由式(42)和式(43)可知,矩阵Ω只对协方差矩阵进行修正,故G͂k也可表示为

式中,λk可视为k时刻下的一个自适应因子,且λk=θ-1k。
从推导可知,鲁棒CKF(R-CKF)算法的本质为对观测向量的误差协方差进行修正,从而使损失函数最小,然后得到系统状态的最佳估计。
R-CKF 算法借鉴了Huber等价权函数的思想,但又与之有着明显区别:Huber-CKF 算法是对观测值的每一维度分别进行检测,当某一维度含有野值时,降低这一维度的权重从而降低野值的影响;而R-CKF算法是根据观测残差的所有维度进行综合评判,然后通过自适应因子λk修正Rk。
当传感器测量值中的野值含量较高时,进行故障隔离可以保障算法的稳定性和精确性。Huber-CKF 算法观测值某一维度含有野值时,无法判断其对整体的影响程度,没法进行整体的取舍,而RCKF 算法可以使用自适应因子λk作为综合判据来判断野值对整体的影响程度,当λk大于阈值β2时,λk→∞,即对这一次的观测值进行隔离。故自适应因子λk的表达式为

对应到CKF 算法,R-CKF 算法只在新息协方差矩阵里加入了自适应因子λk,令Rλ,k=λkRk,将式(24)修正为

当含有大野值时,Rλ,k→∞导致Pzz,k|k-1→∞,则有Kk=0,从而对这一次的观测值进行隔离。
3 鲁棒容积卡尔曼融合算法
假定有N个传感器同步对目标进行测量,则k时刻传感器i的量测方程为


类似地,将式(54)~(55)代入式(49),可得

所以,式(26)滤波增益可重写为

式(68)~(69)中,Rf,λ,k=λf,kRf,k,且λf,k= diag(λ1,k,λ2,k,⋅⋅⋅,λN,k)。观察鲁棒因子λ的定义可知,对于融合中心来说,λi,k中观测残差减去的项应该为融合中心的ẑf,k|k-1,但由于融合系统不带反馈,子系统得不到融合中心的信息,故这里用ẑi,k|k-1来近似。
下面将式(68)~(69)进行变形使它可以利用各传感器的局部预测与局部更新和中心预测x̂k|k-1来表达。即融合中心不直接使用量测来进行全局估计,而仅仅联合局部估计。将式(66)乘以式(67),有
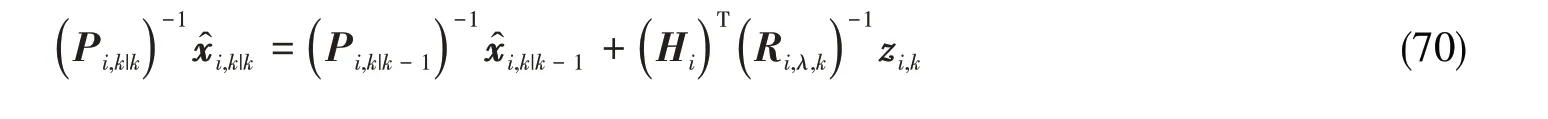
整理可得

4 仿真实验
4.1 仿真条件
本文的研究对象为招商重工(江苏)有限公司建造的CM-163 半潜式起重拆解平台。选取半潜式起重拆解平台的单机起吊工中0~400 t起吊工况下的CSBT-MP-2舱室为仿真对象。CSBT-MP-2舱室的初始参数:舱室总容积为2249 m3,排出水体积占总舱室容积的6%,舱内温度为293 K,外界液位离舱底的距离为12 m,海底阀阀门数量为2,半径为0.495 m,空气压缩机质量流量为5.612 kg∙s-1,舱内初始气压为101272 Pa,初始舱内液位为8.7 m,舱内原始水质量为1394.38 t,海水密度为1.025×103kg∙m-3,海水阻力系数为4.2。
采用蒙特卡洛方法对Huber-CKF 算法、R-CKF 算法、Huber-CKF 融合算法和MSRCKF 算法进行仿真实验,其中Huber-CKF 算法的阈值β为1.345,R-CKF 算法的阈值β1为0.98,β2为5。为了保证实验的合理性,各算例的初始条件相同,蒙特卡洛次数为200次,时间步长为1 s,液位传感器的量测噪声标准差为0.05 m。在上述条件下,使用2 个液位传感器对舱内液位进行测量,其中1 号传感器因为间歇性的机械故障处于半失效状态,2号传感器处于正常工作状态。使用各算法的滤波估计误差值来评价其性能。
算例1:在量测过程中,1号传感器的观测噪声污染率为0.2,2号传感器的观测噪声污染率为0,并将被污染观测的观测噪声的标准差变为正常值的50倍。
算例2:在量测过程中,1号传感器的观测噪声污染率为0.4,2号传感器的观测噪声污染率为0,并将被污染观测的观测噪声的标准差变为正常值的50倍。
4.2 结果分析
算例1~2 的液位误差如图1~2 所示,表1 给出了算例1 和算例2 下各算法的液位误差平均值。其中,Huber-CKF-1和Huber-CKF-2分别对应于1号传感器和2号传感器的Huber-CKF 算法;R-CKF-1和R-CKF-2分别对应于1号传感器和2号传感器的R-CKF 算法;Huber-CKF 融合对应于基于Huber-CKF的融合算法;MSRCKF对应于本文提出的多传感器鲁棒容积卡尔曼融合算法。

表1 各算法的平均液位误差Tab.1 Average level error of algorithms

图1 算例1液位误差图Fig.1 Level error diagram of Example 1
从以上仿真实验可以看出:
(1)如图1和图2所示,在观测值中含有不同比例的野值的情况下,各算法都能随着采样次数的增加趋于收敛。在图1 和图2 中,对于不含野值的2 号传感器观测值,Huber-CKF 算法和R-CKF 算法的估计精度大致一样;Huber-CKF 算法和R-CKF 算法都设有阈值,当超过阈值时才会进行加权,在不含野值的情况下,大多不会超过其阈值,故两者估计精度大致一样。在图1和图2中,随着1号传感器观测值中野值比例的提高,R-CKF算法较Huber-CKF算法在估计精度上的优势越来越明显。

图2 算例2液位误差图Fig.2 Level error diagram of Example 2
(2)如图1 所示,在1 号传感器观测值中野值比例为0.2 时,Huber-CKF 融合与MSRCKF 这两种融合算法均能取得比不含野值的2 号传感器更小的估计误差,这是因为融合中心获得了比单个传感器更多的信息量。如图2 所示,随着1 号传感器观测值中野值比例的提高,Huber-CKF 融合算法的估计误差会增大,其估计误差会比2号传感器的估计误差略大,这是因为其受到的大量不良数据的影响导致其性能出现退化,而MSRCKF算法由于其自适应因子面对大的野值时会采取数据隔离,避免了不良数据的影响,从而得到比2号传感器更小的估计误差。
(3)表1 给出了2 个算例中各算法的所有采样点的平均估计误差。从平均估计误差来看,MS⁃RCKF算法在2个算例中的平均估计误差均是各算法中最小的,其性能更优。
(4)如图1 和图2 所示,所有算法的误差曲线在采样50 次附近均出现了一个大的波动,这是由于运动方程中的状态矢量发生较大改变引起的。此时,排载过程从第一步的舱内建压变为第二步的打开海底阀吹除舱内液体。总体而言,本文所提方法较Huber方法对状态跳变更加不敏感。
由于在实际工程应用中,量测噪声基本不会服从纯高斯分布,也难以保证某个传感器不因发生故障而产生观测野值,故使用2个或2个以上的传感器通过MSRCKF算法可以使系统得到更加稳定可靠的估计值。
5 结 语
为提高半潜式起重平台快速压载舱的液位估计的可靠性和稳定性,本文提出了一种基于多传感器鲁棒容积卡尔曼融合的液位估计算法MSRCKF。针对故障传感器测量含有观测野值的问题,借鉴Huber估计,构造了一个自适应因子来抑制野值的影响,提高了系统的精度和鲁棒性,并通过基于扩展信息滤波的矩阵变换完成了MSRCKF 算法的推导。MSRCKF 算法是一种分布式融合算法,它对融合中心的通信容量要求低,且工程上易于实现。仿真实验证明,MSRCKF 算法在各种算例条件下,均能得到更加稳定可靠的液位估计,具有一定的工程应用价值。
